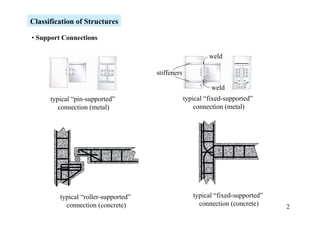
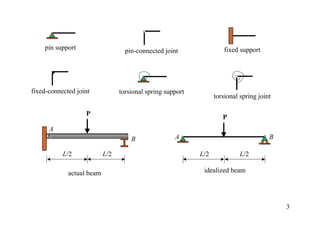
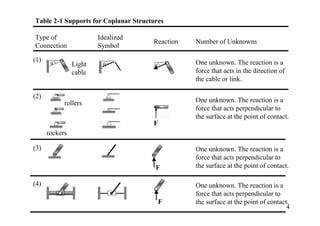
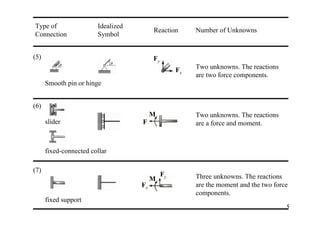
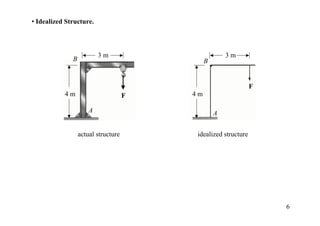
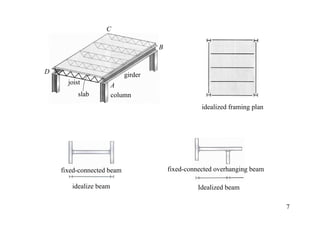
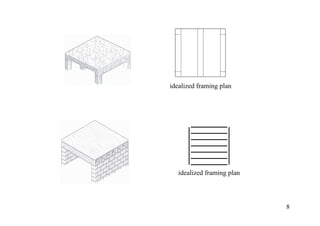
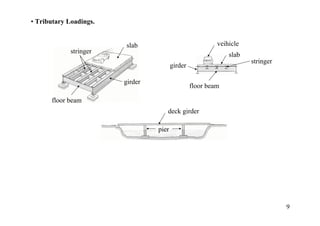
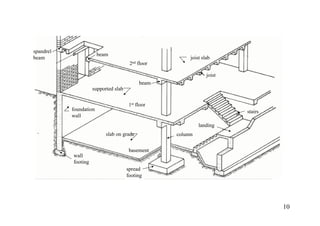
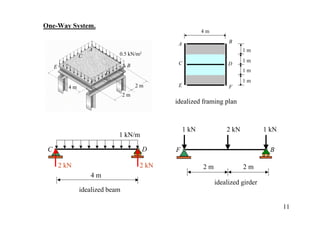
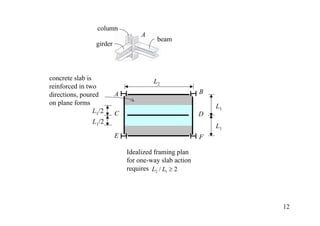
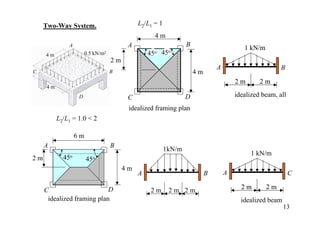
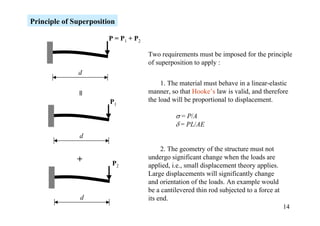
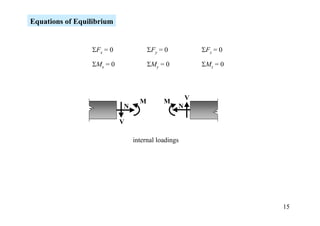
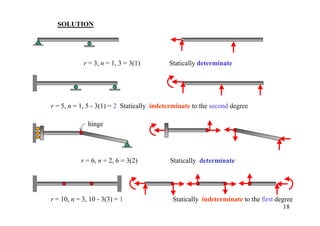
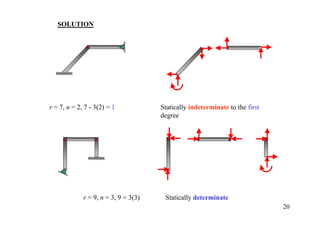
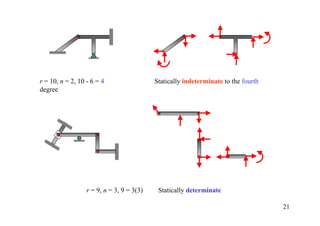
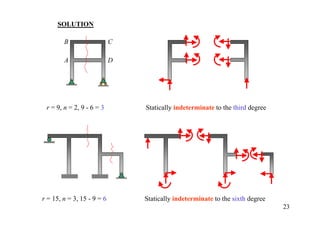
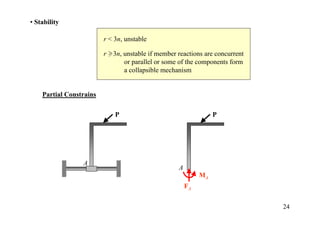
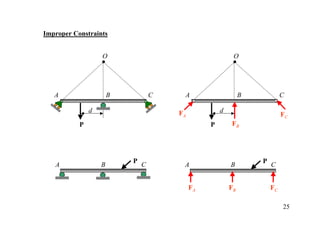
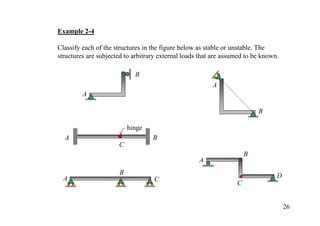
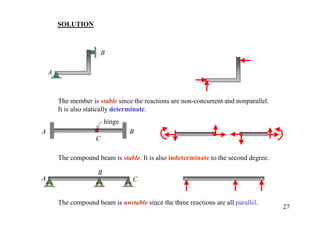
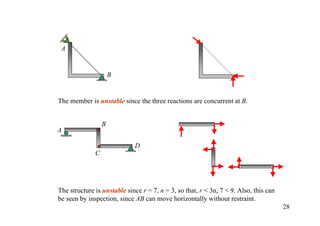
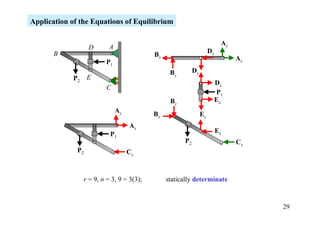
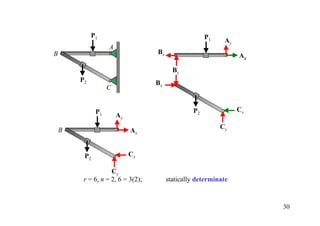
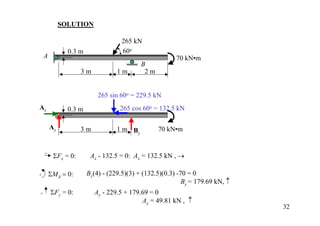
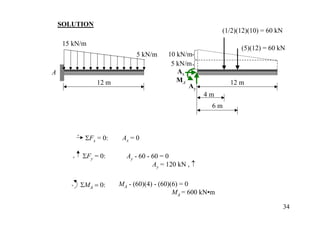
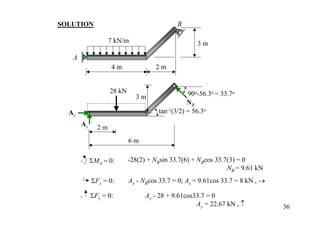
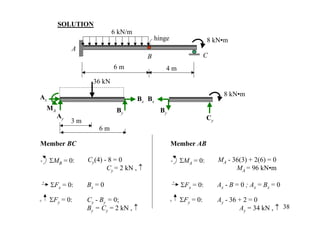
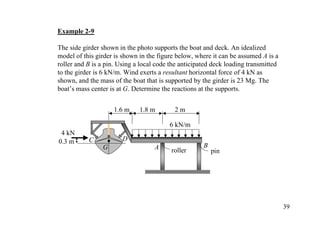
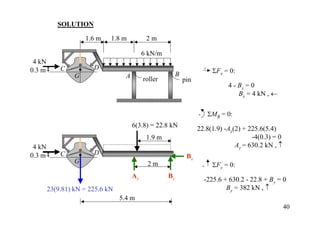
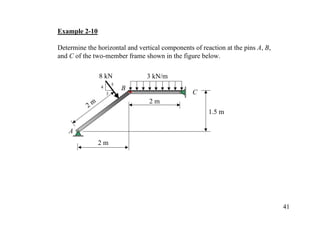
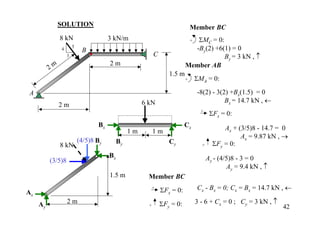
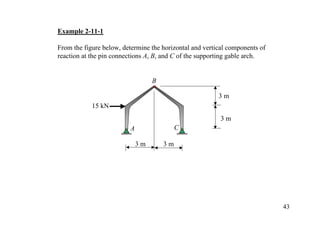
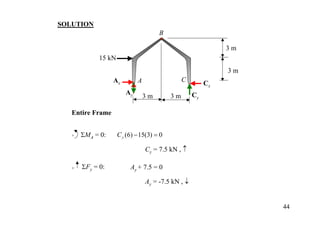
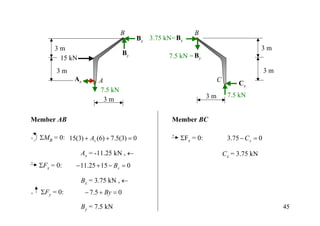
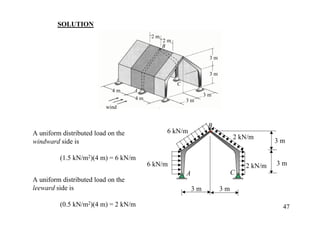
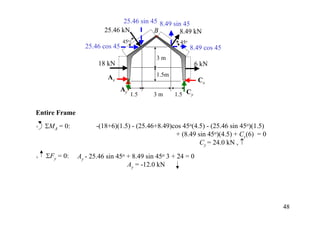
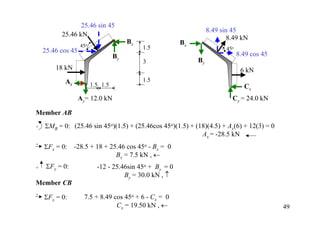
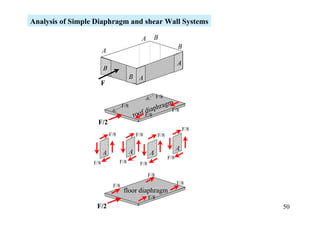
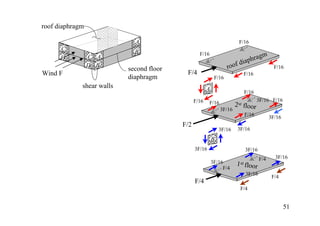
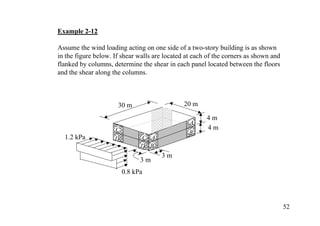
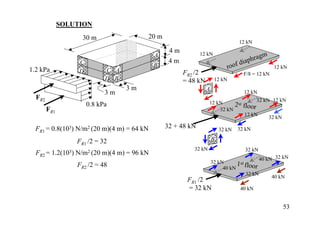
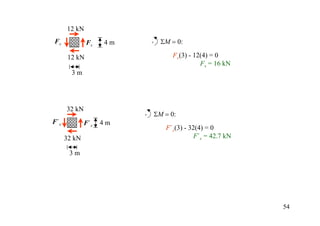
The document discusses the analysis of statically determinate structures, including defining idealized structures, explaining the principle of superposition and equations of equilibrium, classifying structures as determinate or indeterminate, and providing examples of determining reactions on beams and frames through applying the equations of equilibrium.

1. Analysis of Statically Determinate
Structures
! Idealized Structure
! Principle of Superposition
! Equations of Equilibrium
! Determinacy and Stability
! Beams
! Frames
! Gable Frames
! Application of the Equations of Equilibrium
! Analysis of Simple Diaphragm and Shear
Wall Systems Problems
1

2. Classification of Structures
• Support Connections
weld
stiffeners
weld
typical “pin-supported” typical “fixed-supported”
connection (metal) connection (metal)
typical “roller-supported” typical “fixed-supported”
connection (concrete) connection (concrete) 2

3. pin support pin-connected joint fixed support
fixed-connected joint torsional spring support
torsional spring joint
P
P
A
B A B
L/2 L/2 L/2 L/2
actual beam idealized beam
3

4. Table 2-1 Supports for Coplanar Structures
Type of Idealized
Reaction Number of Unknowns
Connection Symbol
(1) One unknown. The reaction is a
θ Light θ θ
cable force that acts in the direction of
the cable or link.
(2)
rollers One unknown. The reaction is a
force that acts perpendicular to
the surface at the point of contact.
F
rockers
(3) One unknown. The reaction is a
force that acts perpendicular to
F the surface at the point of contact.
(4) One unknown. The reaction is a
force that acts perpendicular to
F the surface at the point of contact.
4

5. Type of Idealized
Reaction Number of Unknowns
Connection Symbol
(5) Fy
Fx Two unknowns. The reactions
are two force components.
Smooth pin or hinge
(6)
M Two unknowns. The reactions
slider F are a force and moment.
fixed-connected collar
(7)
Fy Three unknowns. The reactions
M
Fx are the moment and the two force
components.
fixed support
5

6. • Idealized Structure.
3m 3m
B B
F
4m F 4m
A A
actual structure idealized structure
6

7. C
B
D girder
joist A
slab column
idealized framing plan
fixed-connected beam fixed-connected overhanging beam
idealize beam Idealized beam
7

8. idealized framing plan
idealized framing plan
8

9. • Tributary Loadings.
slab veihicle
stringer
slab
stringer
girder
girder
floor beam
floor beam
deck girder
pier
9

10. spandrel
beam
beam joist slab
2nd floor
joist
beam
supported slab
1st floor
foundation stairs
wall
landing
slab on grade column
basement
wall
footing
spread
footing
10

11. One-Way System.
4m
A B
A 1m
C 0.5 kN/m2
C 1m
B D
E
D 1m
F 1m
4m 2m E F
2m
idealized framing plan
1 kN 2 kN 1 kN
1 kN/m
C D F B
2 kN 2 kN 2m 2m
4m
idealized girder
idealized beam
11

12. column
A
beam
girder
concrete slab is L2
reinforced in two
directions, poured A B
on plane forms L1
L1/2 C D
L1/2
L1
E F
Idealized framing plan
for one-way slab action
requires L2 / L1 ≥ 2
12

13. Two-Way System. L2/L1 = 1
4m
A A B
1 kN/m
4m 0.5 kN/m2 45o 45o
2m
A B
C B 4m
2m 2m
4m
D C D idealized beam, all
idealized framing plan
L2/L1 = 1.0 < 2
6m
A B
1kN/m
1 kN/m
2m 45o 45o
4m
A B A C
C D 2m 2m 2m 2m 2m
idealized framing plan idealized beam
13

14. Principle of Superposition
P = P1 + P 2
Two requirements must be imposed for the principle
of superposition to apply :
d
1. The material must behave in a linear-elastic
manner, so that Hooke’s law is valid, and therefore
=
P1 the load will be proportional to displacement.
σ = P/A
δ = PL/AE
d
2. The geometry of the structure must not
+ undergo significant change when the loads are
P2 applied, i.e., small displacement theory applies.
Large displacements will significantly change
and orientation of the loads. An example would
be a cantilevered thin rod subjected to a force at
d its end.
14

15. Equations of Equilibrium
ΣFx = 0 ΣFy = 0 ΣFz = 0
ΣMx = 0 ΣMy = 0 ΣMz = 0
V
M M
N N
V
internal loadings
15

16. Determinacy and Stability
• Determinacy
r = 3n, statically determinate
r > 3n, statically indeterminate
n = the total parts of structure members.
r = the total number of unknown reactive force and moment components
16

17. Example 2-1
Classify each of the beams shown below as statically determinate or statically
indeterminate. If statically indeterminate, report the number of degrees of
indeterminacy. The beams are subjected to external loadings that are assumed to
be known and can act anywhere on the beams.
hinge
hinge
17

18. SOLUTION
r = 3, n = 1, 3 = 3(1) Statically determinate
r = 5, n = 1, 5 - 3(1) = 2 Statically indeterminate to the second degree
hinge
r = 6, n = 2, 6 = 3(2) Statically determinate
r = 10, n = 3, 10 - 3(3) = 1 Statically indeterminate to the first degree
18

19. Example 2-2
Classify each of the pin-connected structures shown in figure below as statically
determinate or statically indeterminate. If statically are subjected to arbitrary
external loadings that are assumed to be known and can act anywhere on the
structures.
19

20. SOLUTION
r = 7, n = 2, 7 - 3(2) = 1 Statically indeterminate to the first
degree
r = 9, n = 3, 9 = 3(3) Statically determinate
20

21. r = 10, n = 2, 10 - 6 = 4 Statically indeterminate to the fourth
degree
r = 9, n = 3, 9 = 3(3) Statically determinate
21

22. Example 2-3
Classify each of the frames shown in figure below as statically determinate or
statically indeterminate. If statically indeterminate, report the number of degrees
of indeterminacy. The frames are subjected to external loadings that are assumed
to be known and can act anywhere on the frames.
B C
A D
22

23. SOLUTION
B C
A D
r = 9, n = 2, 9 - 6 = 3 Statically indeterminate to the third degree
r = 15, n = 3, 15 - 9 = 6 Statically indeterminate to the sixth degree
23

24. • Stability
r < 3n, unstable
r > 3n, unstable if member reactions are concurrent
or parallel or some of the components form
a collapsible mechanism
Partial Constrains
P P
A
A
MA
FA
24

25. Improper Constraints
O O
A B C A B C
d FA d
FC
P P FB
P P
A B C A B C
FA FB FC
25

26. Example 2-4
Classify each of the structures in the figure below as stable or unstable. The
structures are subjected to arbitrary external loads that are assumed to be known.
B
A
A
B
hinge
A B
C
B
A
B D
A C
C
26

27. SOLUTION
B
A
The member is stable since the reactions are non-concurrent and nonparallel.
It is also statically determinate.
hinge
A B
C
The compound beam is stable. It is also indeterminate to the second degree.
B
A C
The compound beam is unstable since the three reactions are all parallel.
27

28. A
B
The member is unstable since the three reactions are concurrent at B.
B
A
D
C
The structure is unstable since r = 7, n = 3, so that, r < 3n, 7 < 9. Also, this can
be seen by inspection, since AB can move horizontally without restraint.
28

29. Application of the Equations of Equilibrium
Ay
D A
B Dx
Bx
Ax
P1
By Dy
P2 E
Dx
C
P1
By Ex
Ay
Bx Ey
Ax
P1 Ex
P2 Cx
P2 Cx
r = 9, n = 3, 9 = 3(3); statically determinate
29

30. P1 P1 Ay
A
B Bx
Ax
By
P2 Bx
C
P1 P2 Cx
Ay
B Cy
Ax
P2 Cx
Cy
r = 6, n = 2, 6 = 3(2); statically determinate
30

31. Example 2-5
Determine the reactions on the beam shown.
150 kN
0.3 m 60o
A 70 kN•m
B
3m 1m 2m
31

32. SOLUTION
265 kN
0.3 m 60o
A 70 kN•m
B
3m 1m 2m
265 sin 60o = 229.5 kN
Ax 0.3 m 265 cos 60o = 132.5 kN
Ay 3m 1 m By 70 kN•m
+ ΣF = 0: Ax - 132.5 = 0: Ax = 132.5 kN , →
x
+ ΣMA = 0: By(4) - (229.5)(3) + (132.5)(0.3) -70 = 0
By = 179.69 kN, ↑
+ ΣFy = 0: Ay - 229.5 + 179.69 = 0
Ay = 49.81 kN , ↑
32

33. Example 2-6
Determine the reactions on the beam shown.
15 kN/m
5 kN/m
A
12 m
33

34. SOLUTION
(1/2)(12)(10) = 60 kN
15 kN/m
(5)(12) = 60 kN
5 kN/m 10 kN/m
5 kN/m
A Ax
12 m MA 12 m
Ay
4m
6m
+ ΣF = 0: Ax = 0
x
+ ΣFy = 0: Ay - 60 - 60 = 0
Ay = 120 kN , ↑
+ ΣMA = 0: MA - (60)(4) - (60)(6) = 0
MA = 600 kN•m
34

35. Example 2-7
Determine the reactions on the beam shown. Assume A is a pin and the support at
B is a roller (smooth surface).
B
7 kN/m 3m
A
4m 2m
35

36. SOLUTION B
7 kN/m 3m
A
4m 2m
28 kN 90o-56.3o = 33.7o
3m
NB
Ax tan-1(3/2) = 56.3o
Ay 2m
6m
+ ΣMA = 0: -28(2) + NBsin 33.7(6) + NBcos 33.7(3) = 0
NB = 9.61 kN
+ ΣF = 0: Ax - NBcos 33.7 = 0; Ax = 9.61cos 33.7 = 8 kN , →
x
+ ΣFy = 0: Ay - 28 + 9.61cos33.7 = 0
Ay = 22.67 kN , ↑ 36

37. Example 2-8
The compound beam in figure below is fixed at A. Determine the reactions at A,
B, and C. Assume that the connection at pin and C is a rooler.
6 kN/m
hinge 8 kN•m
A
B C
6m 4m
37

38. SOLUTION
6 kN/m
hinge 8 kN•m
A
B C
6m 4m
36 kN
Ax 8 kN•m
Bx Bx
MA By By
Ay Cy
3m
6m
Member BC Member AB
+ ΣMB = 0: Cy(4) - 8 = 0 + ΣMA = 0: MA - 36(3) + 2(6) = 0
Cy = 2 kN , ↑ MA = 96 kN•m
+ ΣF = 0: Bx = 0 + ΣF = 0: Ax - B = 0 ; Ax = Bx = 0
x x
+ ΣFy = 0: Cy - By = 0; + ΣFy = 0: Ay - 36 + 2 = 0
By = Cy = 2 kN , ↑ Ay = 34 kN , ↑ 38

39. Example 2-9
The side girder shown in the photo supports the boat and deck. An idealized
model of this girder is shown in the figure below, where it can be assumed A is a
roller and B is a pin. Using a local code the anticipated deck loading transmitted
to the girder is 6 kN/m. Wind exerts a resultant horizontal force of 4 kN as
shown, and the mass of the boat that is supported by the girder is 23 Mg. The
boat’s mass center is at G. Determine the reactions at the supports.
1.6 m 1.8 m 2m
6 kN/m
4 kN
0.3 m C D
G A B
roller pin
39

40. SOLUTION
1.6 m 1.8 m 2m
6 kN/m
4 kN
0.3 m C D + ΣF = 0:
G A B x
roller pin
4 - Bx = 0
Bx = 4 kN , ←
+ ΣMB = 0:
6(3.8) = 22.8 kN
22.8(1.9) -Ay(2) + 225.6(5.4)
1.9 m -4(0.3) = 0
4 kN Ay = 630.2 kN , ↑
0.3 m C D
Bx
G 2m + ΣFy = 0:
Ay By
-225.6 + 630.2 - 22.8 + By = 0
23(9.81) kN = 225.6 kN By = 382 kN , ↑
5.4 m
40

41. Example 2-10
Determine the horizontal and vertical components of reaction at the pins A, B,
and C of the two-member frame shown in the figure below.
8 kN 3 kN/m
5
4 B
3 C
2m
2m
1.5 m
A
2m
41

42. SOLUTION Member BC
8 kN 3 kN/m + ΣMC = 0:
5
4 B -By(2) +6(1) = 0
3 C By = 3 kN , ↑
2m
2m Member AB
1.5 m
+ ΣMA = 0:
A -8(2) - 3(2) +Bx(1.5) = 0
6 kN Bx = 14.7 kN , ←
2m
+ ΣF = 0:
x
Bx Cx Ax + (3/5)8 - 14.7 = 0
1m 1m
Ax = 9.87 kN , →
(4/5)8 By By Cy ΣFy = 0:
8 kN +
Bx Ay - (4/5)8 - 3 = 0
(3/5)8
Ay = 9.4 kN , ↑
1.5 m Member BC
+ ΣF = 0: Cx - Bx = 0; Cx = Bx = 14.7 kN , ←
Ax x
2m ΣFy = 0: 3 - 6 + Cx = 0 ; Cy = 3 kN , ↑
Ay + 42

43. Example 2-11-1
From the figure below, determine the horizontal and vertical components of
reaction at the pin connections A, B, and C of the supporting gable arch.
B
3m
15 kN
3m
A C
3m 3m
43

44. SOLUTION
B
3m
15 kN
3m
Ax A C
Cx
Ay Cy
3m 3m
Entire Frame
+ ΣMA = 0: C y (6) − 15(3) = 0
Cy = 7.5 kN , ↑
+ ΣFy = 0: Ay + 7.5 = 0
Ay = -7.5 kN , ↓
44

45. B B
Bx 3.75 kN= Bx
3m 3m
By 7.5 kN = By
15 kN
3m 3m
Ax A C
Cx
7.5 kN
3m 7.5 kN
3m
Member AB Member BC
+ ΣMB = 0: 15(3) + Ax (6) + 7.5(3) = 0 + ΣF = 0: 3.75 − C x = 0
x
Ax = -11.25 kN , ← Cx = 3.75 kN
+ ΣF = 0: − 11.25 + 15 − Bx = 0
x
Bx = 3.75 kN , ←
+ ΣFy = 0: − 7.5 + By = 0
By = 7.5 kN 45

46. Example 2-11-2
The side of the building in the figure below is subjected to a wind loading that
creates a uniform normal pressure of 1.5 kPa on the windward side and a suction
pressure of 0.5 kPa on the leeward side. Determine the horizontal and vertical
components of reaction at the pin connections A, B, and C of the supporting gable
arch.
2m
2m
B
3m
3m
C
4m A
3m
4m 3m
wind
46

47. SOLUTION
2m
2m
B
3m
3m
C
4m A
3m
4m 3m
wind
B
A uniform distributed load on the 6 kN/m
2 kN/m
windward side is 3m
(1.5 kN/m2)(4 m) = 6 kN/m
6 kN/m 2 kN/m 3m
A C
A uniform distributed load on the
leeward side is 3m 3m
(0.5 kN/m2)(4 m) = 2 kN/m 47

48. 25.46 sin 45 8.49 sin 45
25.46 kN B 8.49 kN
45o 45o
25.46 cos 45 8.49 cos 45
3m
18 kN 6 kN
Ax 1.5m
Cx
Ay
1.5 3m 1.5 Cy
Entire Frame
+ ΣMA = 0: -(18+6)(1.5) - (25.46+8.49)cos 45o(4.5) - (25.46 sin 45o)(1.5)
+ (8.49 sin 45o)(4.5) + Cy(6) = 0
Cy = 24.0 kN , ↑
+ ΣFy = 0: Ay - 25.46 sin 45o + 8.49 sin 45o 3 + 24 = 0
Ay = -12.0 kN
48

49. 25.46 sin 45
8.49 sin 45
25.46 kN
8.49 kN
Bx Bx
45o 1.5
25.46 cos 45 45o
By 8.49 cos 45
3 By
18 kN 6 kN
Ax 1.5
1.5 1.5 Cx
Ay= 12.0 kN Cy = 24.0 kN
Member AB
+ ΣMB = 0: (25.46 sin 45o)(1.5) + (25.46cos 45o)(1.5) + (18)(4.5) + Ax(6) + 12(3) = 0
Ax = -28.5 kN
+ ΣF = 0: -28.5 + 18 + 25.46 cos 45o - B = 0
x x
Bx = 7.5 kN , ←
+ ΣFy = 0: -12 - 25.46sin 45o + By = 0
By = 30.0 kN , ↑
Member CB
+ ΣF = 0: 7.5 + 8.49 cos 45o + 6 - Cx = 0
x
Cx = 19.50 kN , ← 49

50. Analysis of Simple Diaphragm and shear Wall Systems
A B
B
A
A
B
B A
F
F/8
gm
F/8
dia phra F/8
roof F/8
F/2
F/8
F/8 F/8 F/8
A A
A A
F/8
F/8 F/8 F/8
F/8
F/8 F/8
floor diaphragm
F/8
F/2 50

51. roof diaphragm
A F/16
C B F/16
gm
D C A
dia phra
D B
second floor roof F/16
Wind F F/4 F/16
diaphragm F/16
shear walls A F/16
F/16 F/16 3F/16 F/16
2 st floor
3F/16
F/16
3F/16
F/2
3F/16 3F/16
B
3F/16 3F/16
F/4 3F/16
3F/16 1 st floor
F/4
3F/16
F/4
F/4
F/4
51

52. Example 2-12
Assume the wind loading acting on one side of a two-story building is as shown
in the figure below. If shear walls are located at each of the corners as shown and
flanked by columns, determine the shear in each panel located between the floors
and the shear along the columns.
30 m 20 m
4m
A
C 4m
B
1.2 kPa D C A
D B
3m
3m
0.8 kPa
52

53. SOLUTION
30 m 20 m
12 kN
4m 12 kN
A gm
C 4m dia phra
1.2 kPa C A
B roof 12 kN
D FR2 /2 F/8 = 12 kN
D B = 48 kN 12 kN
3m A
3m 12 kN
FR2 32 kN 12 kN
0.8 kPa 12 kN 2 floor
st
FR1 32 kN
12 kN
32 kN
FR1 = 0.8(103) N/m2 (20 m)(4 m) = 64 kN 32 + 48 kN 32 kN 32 kN
FR1 /2 = 32 B
32 kN 32 kN
FR2 = 1.2(103) N/m2 (20 m)(4 m) = 96 kN
40 kN 32 kN
32 kN 1 st floor
FR2 /2 = 48 40 kN
32 kN
40 kN
FR1 /2
= 32 kN 40 kN
53

54. 12 kN
Fv Fv 4m + ΣM = 0:
12 kN Fv(3) - 12(4) = 0
Fv = 16 kN
3m
32 kN
+ ΣM = 0:
F´v F´v 4m
F´v(3) - 32(4) = 0
32 kN F´v = 42.7 kN
3m
54