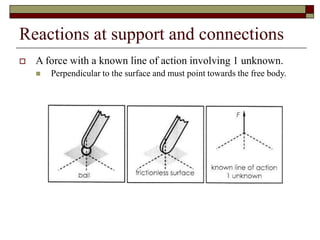
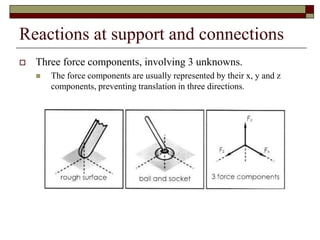
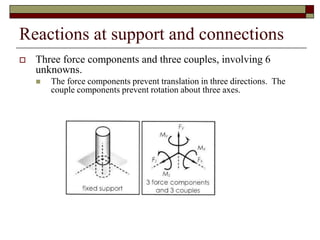
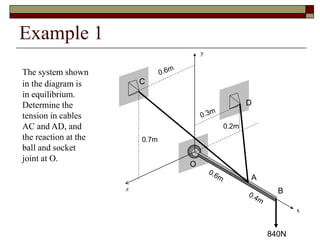
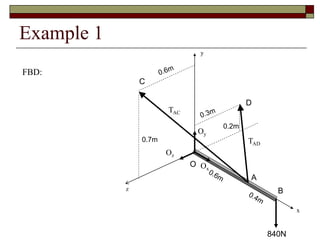
This lecture discusses equilibrium of rigid bodies in 3 dimensions. It covers the equilibrium condition and free body diagram process for 3D rigid bodies. An example problem is presented to demonstrate determining tensions in cables and reaction forces at a ball and socket joint by drawing the free body diagram and applying the equations of equilibrium. Practice is recommended to develop skills in setting up and solving 3D rigid body equilibrium problems.

1. Lecture 8 – Rigid bodies: Equilibrium 3D
What you will learn for today?
1. Equilibrium condition in 3D for rigid bodies
2. FBD for 3D rigid bodies
3. Analysis approach
4. Example and exercise
By: Ts. Dr. Muhammad Hanif Ramlee
Credit to: Prof. Dato’ Ir. Dr. Mohammed Rafiq Abdul Kadir

2. Equilibrium of Rigid Bodies (3D)
 Equilibrium of a particle
 Equilibrium of a rigid body
0
0
0






Z
Y
X
F
F
F






0
0
0
Z
Y
X
F
F
F






0
0
0
Z
Y
X
M
M
M

3. Procedure for drawing FBD
 Draw the boundary of the chosen section and detach /
separate it from all other bodies.
 For body with a mass, put the weight = mg acting at the
centre of gravity (G) of the body in the vertically
downwards direction.
 Input all external forces acting on the body.
 For system involving cables, the force of the cable must act
outwards of the body, i.e. the cable must be in tension.
 Put the reaction/s where the body touches or connected
to a different rigid body.
 The FBD should also include dimensions for the process
of taking moment.

4. Reactions at support and connections
 A force with a known line of action involving 1 unknown.
 Perpendicular to the surface and must point towards the free body.

5. Reactions at support and connections
 Two force components, involving 2 unknowns.
 One perpendicular to the surface and must point towards the free body
and the other 90° to it (tangent to the surface) that can be directed
either way (not both), preventing translation in two directions.

6. Reactions at support and connections
 Three force components, involving 3 unknowns.
 The force components are usually represented by their x, y and z
components, preventing translation in three directions.

7. Reactions at support and connections
 Three force components and one couple, involving 4
unknowns.
 The force components prevent translation in three directions. The
universal joint is designed to allow rotation about two axes.

8. Reactions at support and connections
 Three force components and three couples, involving 6
unknowns.
 The force components prevent translation in three directions. The
couple components prevent rotation about three axes.

9. Reactions at support and connections
 Two force components (and two couples), involving 2 (or 4)
unknowns.
 Mainly designed to prevent translation in two directions, that may also
include two couples. Generally will not exert any appreciable couple
unless otherwise stated.

10. Reactions at support and connections
 Three force components (and two couples), involving 3 (or 5)
unknowns.
 Designed to prevent translation in two directions, that may also
include two couples. Generally will not exert any appreciable couple
unless otherwise stated.

11. IMPORTANTS
 FBD must be drawn for every solution.
 Knowledge on determination of force
components, reactions and ‘cross and dot
products’ (for taking moments) are essential.
 Since there are 6 equations, there can be up to
6 unknowns. For problems with more
unknowns, solve using moment about an axis.
 More than 3 equations, then matrix form is a
best solution of method.

12. Example 1
The system shown
in the diagram is
in equilibrium.
Determine the
tension in cables
AC and AD, and
the reaction at the
ball and socket
joint at O.
840N
0.2m
A
B
O
C
D
0.7m
x
y
z

13. Example 1
FBD:
840N
0.2m
A
B
O
C
D
0.7m
x
y
z
TAD
TAC
Ox
Oy
Oz

14. Equilibrium of rigid bodies
Nj
N 840
840 

 Tension in cable AC, TAC
 
 
 
AC
AC
z
AC
ACz
AC
AC
y
AC
ACy
AC
AC
x
AC
ACx
T
T
d
d
T
T
T
T
d
d
T
T
T
T
d
d
T
T
545
.
0
1
.
1
6
.
0
636
.
0
1
.
1
7
.
0
545
.
0
1
.
1
6
.
0











m
d
m
d
m
d
z
y
x
6
.
0
7
.
0
6
.
0




Nk
T
Nj
T
Ni
T
T AC
AC
AC
AC 545
.
0
636
.
0
545
.
0 




 Solve for the components of the forces:
     
m
d
d
d
d
d
d z
y
x
1
.
1
6
.
0
7
.
0
6
.
0
2
2
2
2
2
2








 Components of the force

15. Equilibrium of rigid bodies
     
m
d
d
d
d
d
d z
y
x
7
.
0
3
.
0
2
.
0
6
.
0
2
2
2
2
2
2









 Tension in cable AD, TAD
 
 
 
AD
AD
z
AD
ADz
AD
AD
y
AD
ADy
AD
AD
x
AD
ADx
T
T
d
d
T
T
T
T
d
d
T
T
T
T
d
d
T
T
429
.
0
7
.
0
3
.
0
286
.
0
7
.
0
2
.
0
857
.
0
7
.
0
6
.
0












m
d
m
d
m
d
z
y
x
3
.
0
2
.
0
6
.
0





Nk
T
Nj
T
Ni
T
T AD
AD
AD
AD 429
.
0
286
.
0
857
.
0 




 Components of the force
 The reaction at O:
Nk
O
Nj
O
Ni
O
O z
y
x 



16. Equilibrium of rigid bodies
 For equilibrium (ΣF=0):
  AD
OA
AC
OA
OB
O T
r
T
r
Nj
r
M 






 840
0
429
.
0
545
.
0
0
286
.
0
636
.
0
840
0
857
.
0
545
.
0












z
AD
AC
y
AD
AC
x
AD
AC
O
T
T
O
T
T
O
T
T
 Solve for the components of the moments (moment about O):
 Moment of the 840N force about O:
 
    Nmk
Nj
mi
M
mi
r
Nj
r
M
O
OB
OB
O
840
840
1
1
840












17. Equilibrium of rigid bodies
 Moment of TAC about O:
   
       
k
T
j
T
M
j
T
k
T
M
Nk
T
Nj
T
Ni
T
mi
M
mi
r
T
r
M
AC
AC
O
AC
AC
O
AC
AC
AC
O
OA
AC
OA
O
3816
.
0
327
.
0
545
.
0
6
.
0
636
.
0
6
.
0
545
.
0
636
.
0
545
.
0
6
.
0
6
.
0



















 Moment of TAD about O:
   
       
k
T
j
T
M
j
T
k
T
M
Nk
T
Nj
T
Ni
T
mi
M
mi
r
T
r
M
AD
AD
O
AD
AD
O
AD
AD
AD
O
OA
AD
OA
O
1716
.
0
257
.
0
429
.
0
6
.
0
286
.
0
6
.
0
429
.
0
286
.
0
857
.
0
6
.
0
6
.
0




















18. Equilibrium of rigid bodies
 For equilibrium (ΣM=0):
 
N
T
N
T
T
T
T
T
T
AC
AD
AD
AD
AD
AD
AC
2
.
1400
4
.
1781
0
1716
.
0
786
.
0
3816
.
0
840
786
.
0
327
.
0
257
.
0










0
1716
.
0
3816
.
0
840
0
257
.
0
327
.
0







AD
AC
AD
AC
T
T
T
T
 Input the values of TAC and TAD into (1), (2), and (3) to get Ox, Oy, Oz.

19. Announcement
 ePPP (Online evaluation for teaching)
 Start from 26 Dec 2022 until 10 Feb 2023

20. Exercise 1
Rod OA of negligible
mass is supported by
cables AB and AC and
loaded with forces as
shown in the diagram. If
the rod is supported by a
ball and socket joint at O,
determine the tension in
cables AB and AC, and
the components of the
reaction at O.
500N
C
B
O
A
D
7m
x
y
z
750N
60°