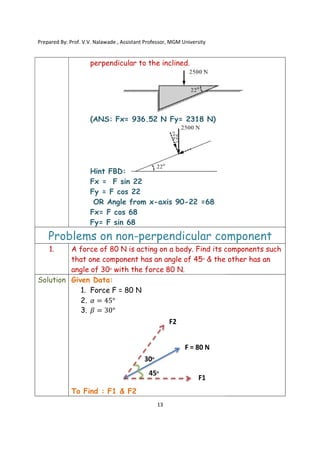
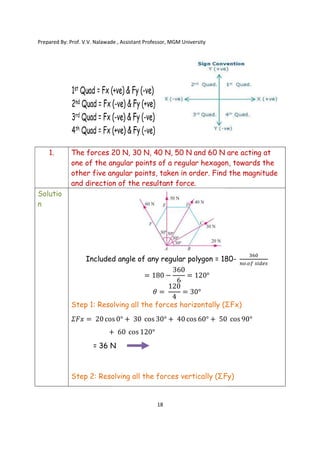
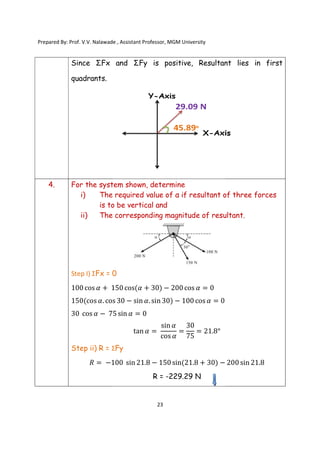
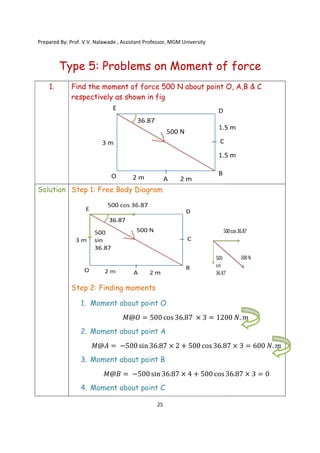
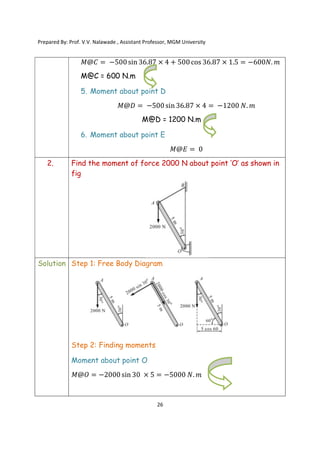
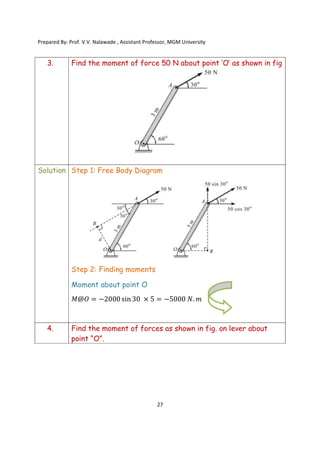
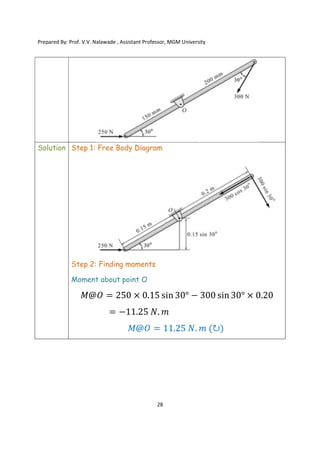
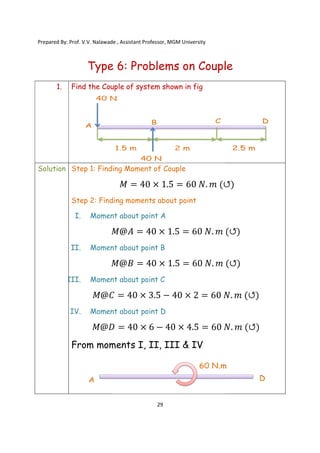
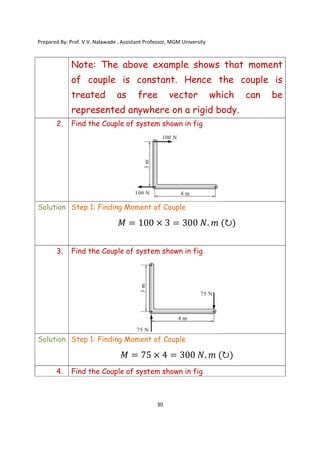
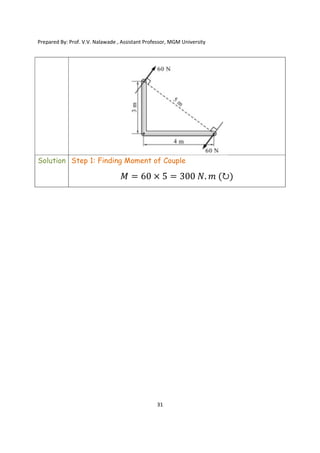
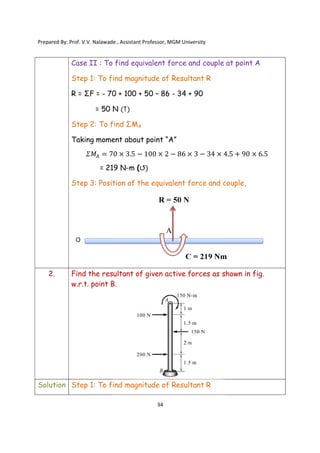
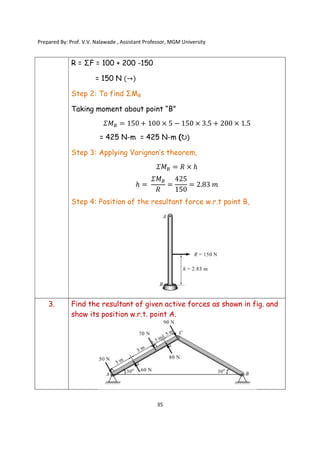
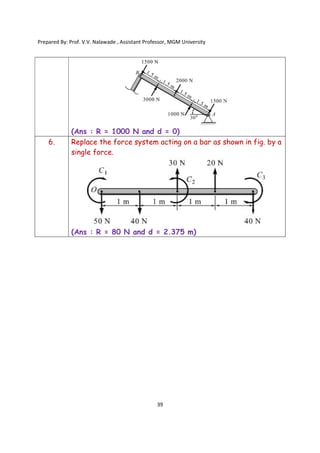
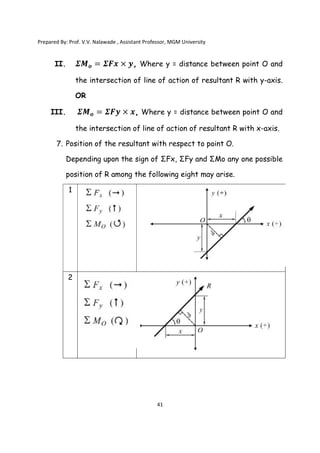
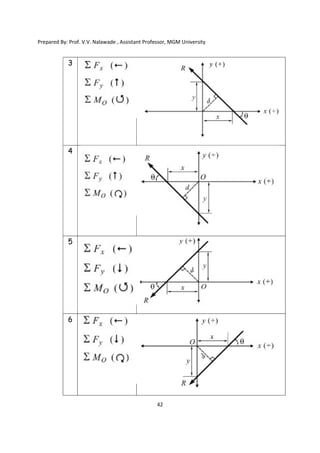
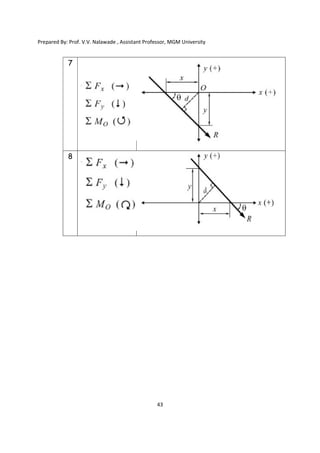
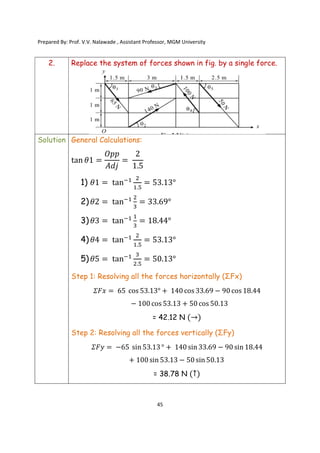
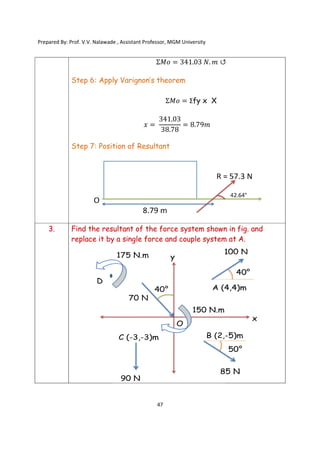
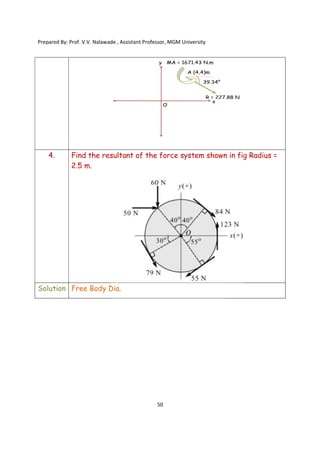
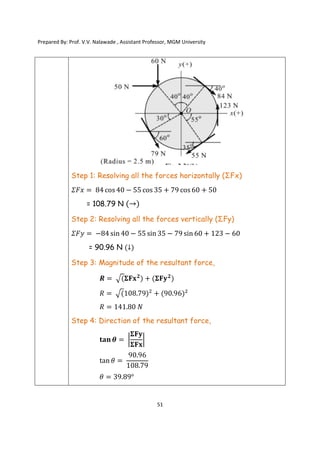
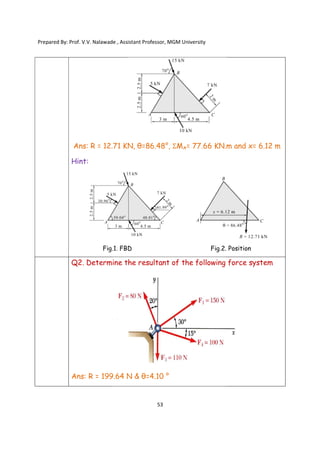
The document contains various problems and solutions on the composition and resolution of forces using the parallelogram and triangle laws. It covers multiple cases with detailed examples and computations, including resultant forces and angles. Prepared by Prof. V.V. Nalawade, the content serves as educational material on physics principles related to force compositions.

1. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM
Type 1: Problems on Composition of Forces by
Parallelogram and Triangle Law
Formulas :
1. Parallelogram Law :
2.Triangle Law :
Sr. No. Examples with solution
1. Find the resultant of the given forces.
Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
1
: Problems on Composition of Forces by
Parallelogram and Triangle Law
Parallelogram Law :
Triangle Law :
Examples with solution
Find the resultant of the given forces.
: Problems on Composition of Forces by
Parallelogram and Triangle Law

2. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM
Solution Case 1: By Parallelogram Law
𝑅 = 4 + 3
R = 5 N
tan ∝ =
∝ =
2. Find the resultant of the given forces.
Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
2
Case 1: By Parallelogram Law
+ 2 × 3 × 4 cos 90°
R = 5 N
3 sin 90°
4 + 3 cos 90°
= 36.87°
Case 2: By Triangle
By Cosine rule
𝑅 = 4 + 3 −
R = 5 N
By Sine rule
𝑅
sin 90°
sin ∝
∝ =
Find the resultant of the given forces.
Triangle Law
By Cosine rule
− 2 × 3 × 4 cos 90°
R = 5 N
By Sine rule
°
=
3
sin ∝
∝ =
3
5
36.87°

3. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM
Solution Case 1: By Parallelogram Law
𝑅
= 50 + 70
R =
tan ∝ =
∝
3. A block is pulled by means of
tension in the rope AB is 2500 KN. Knowing that the
resultant of the two forces at A is directed along X
determine the tension in rope AC and the magnitude of their
resultant force at A.
Solution Given Data:
Q = TAB = 2500 KN, θ = 50
To Find : R and T
Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
3
Parallelogram Law
+ 2 × 50 × 70 cos 60°
R = 104.4 N
70 sin 60°
50 + 70 cos 60°
∝ = 35.5°
Case 2: By Triangle
By Cosine rule
𝑅 = 4 + 3
R = 5 N
By Sine rule
𝑅
sin 90
sin
∝ =
A block is pulled by means of two ropes as shown in fig. the
tension in the rope AB is 2500 KN. Knowing that the
resultant of the two forces at A is directed along X
determine the tension in rope AC and the magnitude of their
resultant force at A.
Given Data: Let P = TAC
= 2500 KN, θ = 50ᵒ , α = 20ᵒ
R and TAC
Triangle Law
By Cosine rule
− 2 × 3 × 4 cos 90°
R = 5 N
By Sine rule
90°
=
3
sin ∝
sin ∝ =
3
5
= 36.87°
two ropes as shown in fig. the
tension in the rope AB is 2500 KN. Knowing that the
resultant of the two forces at A is directed along X- axis,
determine the tension in rope AC and the magnitude of their

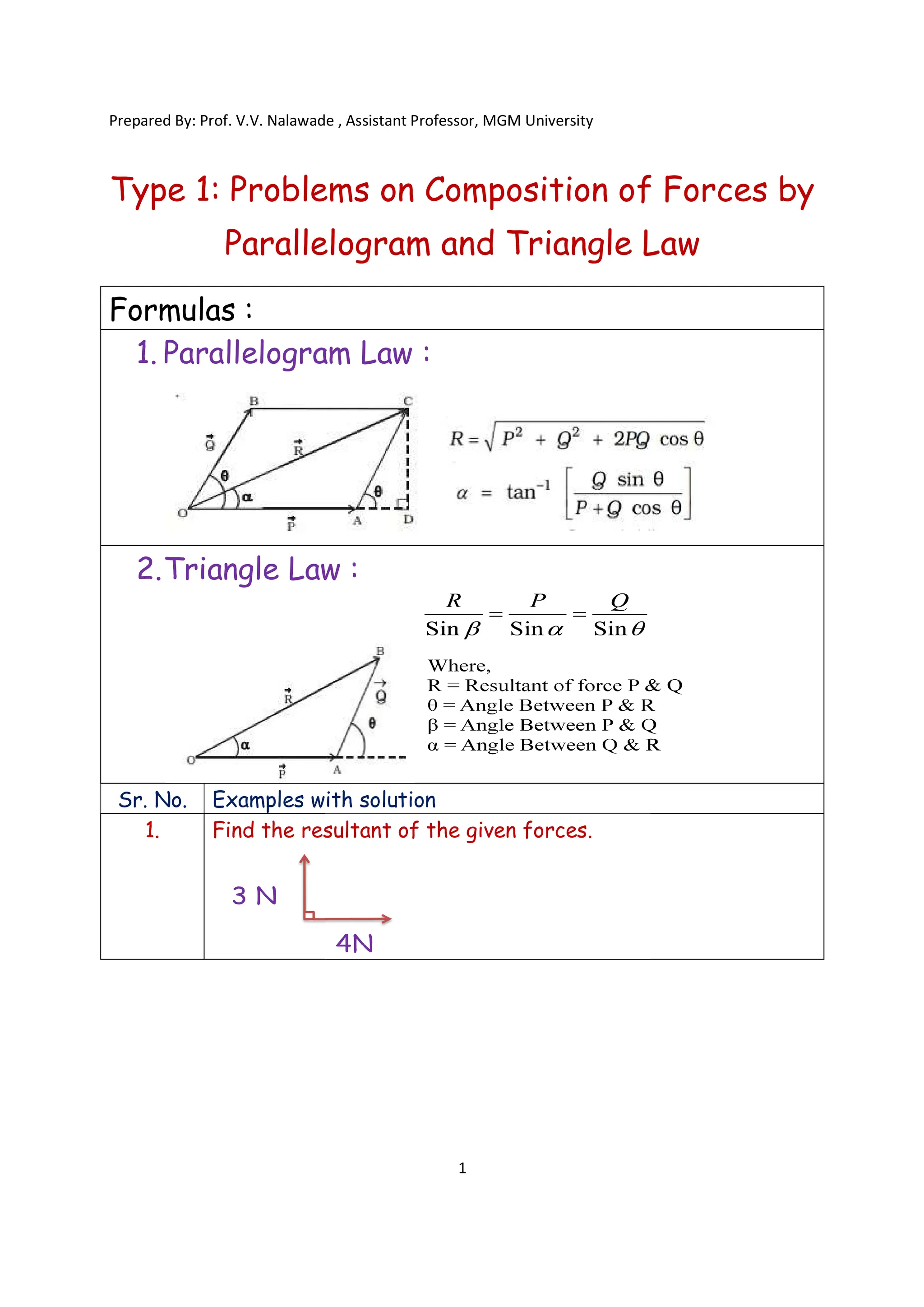
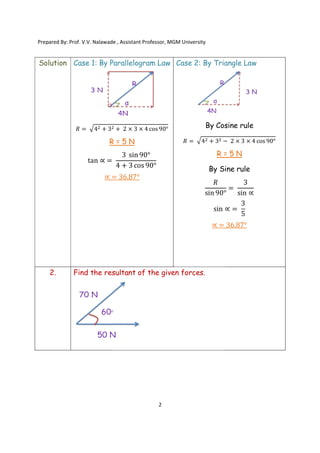
4. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
4
By using Parallelogram Law
Magnitude of resultant is given as
𝑅 = 𝑃 + 2500 + 2 × 𝑃 × 2500 cos 50°
Squaring on both sides
𝑅 = 𝑃 + 2500 + 2 × 𝑃 × 2500 cos 50°………………eqn
1
Direction of resultant is given by
tan 20° =
2500 sin 50°
𝑃 + 2500 cos 50°
Cross multiplication gives
[𝑃 + 2500 cos 50°] tan 20° = 2500 sin 50°
0.3639 P + 584.88 = 1915.11
𝑃 =
1915.11 – 584.88
0.3639
P = 3656.69 KN
Put value of P in eqn
1 we get
𝑅 = 3656.69 + 2500 + 2 × 3656.69 × 2500 cos 50°
R = 5601.22 KN
Final Answer:
1. Tension in Rope AC = 3656.69 KN
2. Magnitude of Resultant R = 5601.22 KN
Assignment:
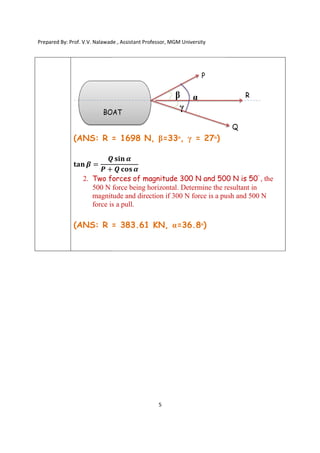
1. A boat is moved uniformly along a canal by two horses
pulling with forces P = 890 N and Q = 1068 N acting at
an angle α = 60ᵒ as shown in the fig. Determine magnitude of
the resultant pull on the boat and the angle β and γ as shown.

5. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM
(ANS: R = 1698 N,
𝐭𝐚𝐧 𝜷 =
𝑸
𝑷 +
2. Two forces of magnitude 300 N and 500 N is 50
500 N force being horizontal. Determine the resultant
magnitude and direction if 300 N force is a push and 500 N
force is a pull.
(ANS: R =
Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
5
(ANS: R = 1698 N, β=33ᵒ, γ = 27ᵒ)
𝑸 𝐬𝐢𝐧 𝜶
+ 𝑸 𝐜𝐨𝐬𝜶
Two forces of magnitude 300 N and 500 N is 50
500 N force being horizontal. Determine the resultant
magnitude and direction if 300 N force is a push and 500 N
force is a pull.
(ANS: R = 383.61 KN, α=36.8ᵒ)
Two forces of magnitude 300 N and 500 N is 50ᵒ
, the
500 N force being horizontal. Determine the resultant in
magnitude and direction if 300 N force is a push and 500 N

6. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
6
Type 2: Problems on Resolution of Forces by
Parallelogram and Triangle Law
1. Two forces act at an angle of 120ᵒ. The bigger force is of 40
N and the resultant is perpendicular to the smaller one. Find
the smaller force.
Solution Given Data:
1. Angle between the forces ∆AOC = θ = 120ᵒ
2. Bigger force (P) = 40 N
3. Angle between resultant (R) and smaller force (Q) ∆BOC =β=
90ᵒ
Step 1: To find the ∆AOB
From geometry of fig, we can find the ∆AOB,
α = θ- β = 120ᵒ - 90ᵒ = 30ᵒ
Step 2: To find Q
we know that,
tan ∝ =
𝑄 sin 𝜃
𝑃 + 𝑄 cos 𝜃
tan 30ᵒ =
𝑄 sin 120°
40 + 𝑄 cos 120°
0.577 =
0.866 𝑄
40 − 0.5 𝑄
0.577*(40-0.5Q) = 0.866 Q

7. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
7
Q = 20 N
ANS: The smaller force Q = 20N
2. Resolve the 2000 N force into two oblique components one
acting along AB and the other acting along BC.
Solution Given Data:
1. Angle between the forces ∆AOC = 120ᵒ
2. Bigger force (F1) = 40 N
3. Angle between resultant and smaller force (F2) ∆BOC = 90ᵒ
Step 1: To find the θ
By triangle law, we have
tan θ = 2/3
θ = tan
2
3
θ = 33.69ᵒ
Step 2: To Find Forces

8. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
8
By sine rule, we have
2000
sin 33.69°
=
𝐹𝐴𝐵
sin 90°
=
𝐹𝐵𝐶
sin 56.31°
2000
sin 33.69°
=
𝐹𝐴𝐵
sin 90°
𝐹𝐴𝐵 =
2000 sin 90°
sin 33.69
𝐹𝐴𝐵 =
2000 ∗ 1
0.5546
𝐹𝐵𝐶 =
2000 sin 56.31°
sin 33.69
FAB = 3605.56 N
FBC = 3000 N
Assignment
1. Find the magnitude of the two forces, such that
if they act at right angles, their resultant is √10
N. but if they act at 60ᵒ, their resultant is √13N.
10 = 𝑃 + 𝑄 ………………………eq1
13 = 𝑃 + 𝑄 + 𝑃𝑄……………………eq2
PQ= 3……………………………….eq3
𝑄 = ANS: Q = 3N & P = 1 N)

9. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
9
Type 3: Problems on Resolution of Forces
into Rectangular and Oblique components of
force
Formulas for Rectangular Components
 Fx = F. Cos θ
 Fy = F. Sin θ

Formulas for Oblique Components
 𝐹1 =
( )
 𝐹2 =
( )
 Or you may also apply Parallelogram law & Triangle Law
to this type of problem.
1. Resolve a force of 30N acting North-East away from the
point.
Solution Given Data:
1. F = 30 N acting N-E

10. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM
Step 1: To find
Step 2: To Find
2. A force P is acting on a block as shown in fig. if horizontal
rectangular component of P is 40 N acting to the
find the y component of P.
Solution Given Data:
1. Horizontal rectangular component of P
2. tan 𝜃 =
3. FBD
Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
10
To find Fx
Fx = F cos θ = 30 cos 45ᵒ
= 21.21 N
To Find Fy
Fy = F sin θ = 30 sin 45ᵒ
= 21.21 N
A force P is acting on a block as shown in fig. if horizontal
rectangular component of P is 40 N acting to the
find the y component of P.
Given Data:
Horizontal rectangular component of P = 40 N
= = 36.87°
A force P is acting on a block as shown in fig. if horizontal
rectangular component of P is 40 N acting to the left then
= 40 N

11. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
11
Step 1: To find magnitude of P
Fx = F Cos θ
40 = P cos θ
40 = P cos (30+36.87)
𝑃 =
. °
P = 101.82 N
Step 2: To Find Py
Py = P sin θ = 101.82 sin 30ᵒ
Py = 50.91 N
3. A force 360 N is acting on a block as shown in fig. find the
components of forces along the x-y axis which are parallel
and perpendicular to the inclined.
Solution Given Data:
1. Force P = 360 N
2. Θ1 = tan-1
¾ = 36.87ᵒ
3. Θ2 = tan-1
2/3 = 33.69ᵒ
4

12. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
12
To Find : Px & Py
Step 1: To find magnitude of Px
Px = P cos (θ1+ θ2)
= 360 cos (70.56)
Px = 119.82 N
Step 2: To Find magnitude of Py
Py = P sin (θ1+ θ2)
= 360 sin (70.56)
Py = 339.48 N
ASSIGNMENT
1. Resolve a force of 40 KN inclined at 150ᵒ with x-axis
acting towards the point.
(ANS: Fx= 34.64 KN Fy= -20 KN)
2. Resolve the 2500 N force acting vertically on wedge
having inclination 22ᵒ as shown in fig. into two
components one acting along inclined 22ᵒ and the other

13. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM
perpendicular to the inclined.
(ANS: Fx=
Hint FBD:
Fx = F sin 22
Fy = F cos 22
OR Angle from x
Fx= F cos 68
Fy= F sin 68
Problems on non
1. A force of 80 N is acting on a body. Find its components such
that one component has an angle of 45
angle of 30ᵒ
Solution Given Data:
1. Force F
2. 𝛼 = 45°
3. 𝛽 = 30°
To Find : F1 &
Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
13
perpendicular to the inclined.
(ANS: Fx= 936.52 N Fy= 2318 N)
Hint FBD:
Fx = F sin 22
Fy = F cos 22
OR Angle from x-axis 90-22 =68
Fx= F cos 68
Fy= F sin 68
on non-perpendicular component
A force of 80 N is acting on a body. Find its components such
that one component has an angle of 45ᵒ & the other has an
with the force 80 N.
Given Data:
F = 80 N
°
°
F1 & F2
perpendicular component
A force of 80 N is acting on a body. Find its components such
& the other has an

14. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM
Step 1: To find magnitude of
Step 2: To Find magnitude of
2. A force of 2000 N is acts at an angle of 60°
Find its components along 105° & 330° with X
Solution Given Data:
1) F = 2000 N
2) α = 105
3) β = (360
Step 1: To find magnitude of F1
Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
14
To find magnitude of F1
𝑭𝟏 =
𝑭 𝐬𝐢𝐧 𝜷
𝐬𝐢𝐧(𝜶 + 𝜷)
𝐹1 =
80 sin 30°
sin(45° + 30°)
F1 = 41.41 N
To Find magnitude of F2
𝑭𝟐 =
𝑭 𝐬𝐢𝐧 𝜶
𝐬𝐢𝐧(𝜶 + 𝜷)
𝐹2 =
80 sin 45°
sin(45° + 30°)
F2 = 58.56 N
A force of 2000 N is acts at an angle of 60° with X
Find its components along 105° & 330° with X
Given Data:
= 2000 N
105 – 60 = 45°
(360-330) + 60 = 90°
To find magnitude of F1
𝑭𝟏 =
𝑭 𝐬𝐢𝐧 𝜷
𝐬𝐢𝐧(𝜶 + 𝜷)
𝐹1 =
2000 sin 90°
sin(45° + 90°)
with X-axis.
Find its components along 105° & 330° with X-axis.

15. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM
Step 2: To Find magnitude of F2
Ans:
1. Component along 105°
2. Component along 330° = 2000 N
3. The resultant of two forces in a plane is 800 N at 60° with x
axis. One force is 160N at 30° with x axis. Determine the
missing force & its inclination.
Solution Given Data:
1. F = 800 N
2. F1 = 160 N
3. α = 60
To find: F2 & β
Step 1: To find β
Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
15
F1 = 2828.43 N
To Find magnitude of F2
𝑭𝟐 =
𝑭 𝐬𝐢𝐧 𝜶
𝐬𝐢𝐧(𝜶 + 𝜷)
𝐹2 =
2000 sin 45°
sin(45° + 90°)
F2 = 2000 N
Component along 105° = 2828.43 N
Component along 330° = 2000 N
The resultant of two forces in a plane is 800 N at 60° with x
force is 160N at 30° with x axis. Determine the
missing force & its inclination.
Given Data:
F = 800 N
F1 = 160 N
α = 60 – 30 = 30°
F2 & β
To find β
𝑭𝟏 =
𝑭 𝐬𝐢𝐧 𝜷
𝐬𝐢𝐧(𝜶 + 𝜷)
The resultant of two forces in a plane is 800 N at 60° with x-
force is 160N at 30° with x axis. Determine the

16. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
16
160 =
800 sin 𝛽
sin(30 + 𝛽)
160 (sin (30+β)) = 800 sin β
80 cos β = 661.44 sin β
sin 𝛽
cos 𝛽
=
80
661.44
tan𝛽 = 0.1209
β = 6.89°
Step 2: To Find magnitude of F2
𝑭𝟐 =
𝑭 𝐬𝐢𝐧 𝜶
𝐬𝐢𝐧(𝜶 + 𝜷)
𝐹2 =
800 sin 30
sin(30 + 6.89)
F2 = 666.35 N
ASSIGNMENT
1. Resolve a force of 60 N into two components F and 80
N as shown in fig. Find the value of F and θ
(ANS: F = 90.82 N and θ = 79.46°)

17. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
17
Type 4: Problems on Resultant of concurrent
force system using Method of Resolution
 If the number of forces is more than two, then its resultant can
be found out conveniently by the METHOD OF RESOLUTION.
 STEPWISE PROCEDURE OF METHOD OF RESOLUTION:
1. Resolve all forces horizontally and find the algebraic sum of all
the horizontal components (i.e., ΣFx)
2. Resolve all forces vertically and find the algebraic sum of all
the vertical components (i.e., ΣFy).
3. The resultant R of the given forces will be given by the
equation:
𝑹 = (𝚺𝐅𝐱𝟐
) + (𝚺𝐅𝐲𝟐
)
4. The resultant force will be inclined at an angle θ, with the
horizontal, such that
tan𝜃 =
ΣFy
ΣFx
5. Position of the resultant

18. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM
1. The forces 20 N, 30 N, 40 N, 50 N and 60 N are acting at
one of the angular points of a regular hexagon, towards the
other five angular points, taken in order. Find the
and direction of the resultant force.
Solutio
n
Included angle of any regular polygon = 180
Step 1: Resolving all the forces horizontally (ΣFx)
𝛴𝐹𝑥 = 20 cos
+
= 36 N
Step 2: Resolving all the forces vertically (ΣFy)
Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
18
The forces 20 N, 30 N, 40 N, 50 N and 60 N are acting at
one of the angular points of a regular hexagon, towards the
other five angular points, taken in order. Find the
and direction of the resultant force.
Included angle of any regular polygon = 180
= 180 −
360
6
= 120°
𝜃 =
120
4
= 30°
Resolving all the forces horizontally (ΣFx)
cos 0° + 30 cos 30° + 40 cos 60° + 50
+ 60 cos 120°
= 36 N
Resolving all the forces vertically (ΣFy)
The forces 20 N, 30 N, 40 N, 50 N and 60 N are acting at
one of the angular points of a regular hexagon, towards the
other five angular points, taken in order. Find the magnitude
Included angle of any regular polygon = 180-
.
Resolving all the forces horizontally (ΣFx)
50 cos 90°
Resolving all the forces vertically (ΣFy)

19. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM
𝛴𝐹𝑦 = 20
= 151.6 N
Step 3: Magnitude of the resultant force,
Step 4: Direction of the resultant force,
Step 5: Position of the resultant force,
2. The following forces act at a point :
i. 20 N inclined at 30
ii. 25 N towards North,
iii. 30 N towards North West, and
iv. 35 N inclined at 40
Find the magnitude and direction of the resultant force.
Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
19
20 sin 0° + 30 sin 30° + 40 sin 60° +
+ 60 sin 120°
= 151.6 N
Magnitude of the resultant force,
𝑹 = (𝚺𝐅𝐱𝟐
) + (𝚺𝐅𝐲𝟐
𝑅 = (36) + (151.6)
𝑅 = 155.8 𝑁
Direction of the resultant force,
𝐭𝐚𝐧 𝜽 =
𝚺𝐅𝐲
𝚺𝐅𝐱
tan 𝜃 =
151.6
36
𝜃 = 76.6°
Position of the resultant force,
The following forces act at a point :
20 N inclined at 30ᵒ towards North of East,
25 N towards North,
towards North West, and
35 N inclined at 40ᵒ towards South of West.
Find the magnitude and direction of the resultant force.
+ 50 sin 90°
)
towards North of East,
towards South of West.
Find the magnitude and direction of the resultant force.

20. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
20
Solutio
n
Step 1: Resolving all the forces horizontally (ΣFx)
𝛴𝐹𝑥 = 20 cos 30° + 25 cos 90° + 30 cos 135° + 35 cos 220°
= - 30.7 N
Step 2: Resolving all the forces vertically (ΣFy)
𝛴𝐹𝑦 = 20 sin 30° + 25 sin 90° + 30 sin 135° + 35 sin 220°
= 33.7 N
Step 3: Magnitude of the resultant force,
𝑹 = (𝚺𝐅𝐱𝟐
) + (𝚺𝐅𝐲𝟐
)
𝑅 = (−30.7) + (33.7)
𝑅 = 45.6 𝑁
Step 4: Direction of the resultant force,
𝐭𝐚𝐧 𝜽 =
𝚺𝐅𝐲
𝚺𝐅𝐱
tan 𝜃 =
33.7
−30.7
𝜃 = 47.7°
Step 5: Position of the resultant force,

21. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM
Since ΣFx is negative and ΣFy is positive, Resultant lies
between second
Therefore acute angle of the resultant = 180
3. The Striker of carom board laying on the board is being
pulled by four players as shown in fig. the players are sitting
exactly at the centre of the four sides. Determine the
resultant of forces in magnitude and direction.
Solutio
n
General calculation
𝐭𝐚𝐧 𝜽𝟏 =
𝟏𝟓𝟎
𝟓𝟎𝟎
𝐭𝐚𝐧 𝜽𝟐 =
𝟓𝟓𝟎
𝟏𝟎𝟎
Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
21
Since ΣFx is negative and ΣFy is positive, Resultant lies
between second quadrants.
Therefore acute angle of the resultant = 180
Striker of carom board laying on the board is being
pulled by four players as shown in fig. the players are sitting
exactly at the centre of the four sides. Determine the
resultant of forces in magnitude and direction.
General calculation : Respective angles of each player
𝟏𝟓𝟎
𝟓𝟎𝟎
= 𝟏𝟔. 𝟕°
𝟓𝟓𝟎
𝟏𝟎𝟎
= 𝟕𝟗. 𝟕°
Since ΣFx is negative and ΣFy is positive, Resultant lies
Therefore acute angle of the resultant = 180ᵒ - 47.7ᵒ = 132.3ᵒ
Striker of carom board laying on the board is being
pulled by four players as shown in fig. the players are sitting
exactly at the centre of the four sides. Determine the
resultant of forces in magnitude and direction.
Respective angles of each player

22. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM
𝐭𝐚𝐧 𝜽𝟑 =
𝟏𝟓𝟎
𝟑𝟎𝟎
𝐭𝐚𝐧 𝜽𝟒 =
𝟐𝟓𝟎
𝟏𝟎𝟎
Step 1: Resolving all the forces
horizontally (ΣFx)
𝛴𝐹𝑥 = 20
= 20.25
Step 2: Resolving all the forces vertically (ΣFy)
𝛴𝐹𝑦 = 20 sin
= 20.89
Step 3: Magnitude of the resultant
Step 4: Direction of the resultant force,
Step 5: Position of the resultant force,
Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
22
𝟏𝟓𝟎
𝟑𝟎𝟎
= 𝟐𝟔. 𝟓𝟔°
𝟐𝟓𝟎
𝟏𝟎𝟎
= 𝟔𝟖. 𝟐°
Resolving all the forces
horizontally (ΣFx)
20 cos 16.7° + 25 cos 79.7° − 10
+ 15 cos 68.2°
20.25 N
Resolving all the forces vertically (ΣFy)
sin 16.7° + 25 sin 79.7° + 10 sin 26.56
20.89 N
Magnitude of the resultant force,
𝑹 = (𝚺𝐅𝐱𝟐
) + (𝚺𝐅𝐲𝟐
𝑅 = (20.25) + (20.89
𝑅 = 29.09 𝑁
Direction of the resultant force,
𝐭𝐚𝐧 𝜽 =
𝚺𝐅𝐲
𝚺𝐅𝐱
tan 𝜃 =
20.89
20.25
𝜃 = 45.89°
Position of the resultant force,
10 cos 26.56°
Resolving all the forces vertically (ΣFy)
56° − 15 sin 68.2°
)
89)

23. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM
Since ΣFx and ΣFy is positive, Resultant lies
quadrants.
4. For the system shown, determine
i) The required value of α if resultant of three forces
is to be vertical and
ii) The corresponding magnitude of resultant.
Step I) ƩFx = 0
100 cos 𝛼 + 150
150(cos 𝛼. cos
30 cos 𝛼 − 75
Step ii) R = Ʃ
𝑅 = −100
Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
23
Since ΣFx and ΣFy is positive, Resultant lies
the system shown, determine
The required value of α if resultant of three forces
is to be vertical and
The corresponding magnitude of resultant.
Fx = 0
150 cos(𝛼 + 30) − 200cos 𝛼 = 0
cos 30 − sin 𝛼. sin 30) − 100 cos 𝛼 = 0
75 sin 𝛼 = 0
tan 𝛼 =
sin 𝛼
cos 𝛼
=
30
75
= 21.8°
ƩFy
100 sin 21.8 − 150 sin(21.8 + 30) −
R = -229.29 N
Since ΣFx and ΣFy is positive, Resultant lies in first
The required value of α if resultant of three forces
The corresponding magnitude of resultant.
200 sin 21.8

24. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
24
(ANS: α = 21.8ᵒ & R = 229.29 N)
5.

25. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM
Type 5: Problems on
1. Find the moment of force 500 N about
respectively as shown in fig
Solution Step 1: Free Body Diagram
Step 2: Finding moments
1. Moment about point O
2. Moment about point A
𝑀@𝐴 =
3. Moment about
𝑀@
4. Moment about point C
Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
25
: Problems on Moment of force
Find the moment of force 500 N about point O, A,B & C
respectively as shown in fig
Free Body Diagram
Finding moments
Moment about point O
𝑀@𝑂 = 500 cos 36.87 × 3 = 1200
Moment about point A
= −500 sin 36.87 × 2 + 500 cos 36.87
Moment about point B
@𝐵 = −500 sin 36.87 × 4 + 500 cos
Moment about point C
Moment of force
point O, A,B & C
1200 𝑁. 𝑚
87 × 3 = 600 𝑁. 𝑚
36.87 × 3 = 0

26. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
26
𝑀@𝐶 = −500sin 36.87 × 4 + 500cos 36.87 × 1.5 = −600𝑁. 𝑚
M@C = 600 N.m
5. Moment about point D
𝑀@𝐷 = −500sin 36.87 × 4 = −1200 𝑁. 𝑚
M@D = 1200 N.m
6. Moment about point E
𝑀@𝐸 = 0
2. Find the moment of force 2000 N about point ‘O’ as shown in
fig
Solution Step 1: Free Body Diagram
Step 2: Finding moments
Moment about point O
𝑀@𝑂 = −2000 sin 30 × 5 = −5000 𝑁. 𝑚

27. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
27
3. Find the moment of force 50 N about point ‘O’ as shown in fig
Solution Step 1: Free Body Diagram
Step 2: Finding moments
Moment about point O
𝑀@𝑂 = −2000 sin 30 × 5 = −5000 𝑁. 𝑚
4. Find the moment of forces as shown in fig. on lever about
point “O”.

28. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
28
Solution Step 1: Free Body Diagram
Step 2: Finding moments
Moment about point O

29. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM
Type
1. Find the Couple of system shown in fig
Solution Step 1: Finding
Step 2: Finding moments
I. Moment about point A
II. Moment about point B
III. Moment about point C
IV. Moment about point
From moments I, II, III & IV
Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
29
Type 6: Problems on Couple
Couple of system shown in fig
Finding Moment of Couple
Finding moments about point
Moment about point A
Moment about point B
Moment about point C
Moment about point D
moments I, II, III & IV
Couple

30. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
30
Note: The above example shows that moment
of couple is constant. Hence the couple is
treated as free vector which can be
represented anywhere on a rigid body.
2. Find the Couple of system shown in fig
Solution Step 1: Finding Moment of Couple
3. Find the Couple of system shown in fig
Solution Step 1: Finding Moment of Couple
4. Find the Couple of system shown in fig

31. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
31
Solution Step 1: Finding Moment of Couple

32. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM
Type 7: Problems on
force system using Method of Resolution
 STEPWISE PROCEDURE OF METHOD OF RESOLUTION:
1. Find resultant R
parallel forces considering proper sign convention.
2. Find ΣMo. Take the algebraic sum moment of forces
point (say O)
(+𝒗𝒆
3. Apply Varignon’s theorem,
Where d = perpendicular distance between line of action of
R and reference point O
4. Position of the resultant
Resultant may
O at a distance d, depending on the sign of ΣF & ΣMo.
Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
32
: Problems on Resultant of parallel
force system using Method of Resolution
STEPWISE PROCEDURE OF METHOD OF RESOLUTION:
resultant R = Σ F. Take the algebraic sum of all the
parallel forces considering proper sign convention.
(+𝒗𝒆 ↑) ( −𝒗𝒆 ↓)
Find ΣMo. Take the algebraic sum moment of forces
(say O) considering proper sign convention.
𝒗𝒆 ↻ −𝑪𝒍𝒐𝒄𝒌𝒘𝒊𝒔𝒆) ( −𝒗𝒆 ↺ −𝒂𝒏𝒕𝒊𝒄𝒍𝒐𝒄𝒌𝒘𝒊𝒔𝒆
Apply Varignon’s theorem, 𝜮𝑴𝒐 = 𝑹 × 𝒅
Where d = perpendicular distance between line of action of
R and reference point O.
Position of the resultant with respect to point O.
Resultant may lie to the right or left of the reference point
O at a distance d, depending on the sign of ΣF & ΣMo.
Resultant of parallel
force system using Method of Resolution
STEPWISE PROCEDURE OF METHOD OF RESOLUTION:
= Σ F. Take the algebraic sum of all the
parallel forces considering proper sign convention.
Find ΣMo. Take the algebraic sum moment of forces about a
ing proper sign convention.
𝒂𝒏𝒕𝒊𝒄𝒍𝒐𝒄𝒌𝒘𝒊𝒔𝒆)
Where d = perpendicular distance between line of action of
with respect to point O.
or left of the reference point
O at a distance d, depending on the sign of ΣF & ΣMo.

33. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM
1. Find the resultant of following force system and also find the
equivalent force and couple at point A of the same force
system shown in fig.
Solution Case I : To find resultant of
Step 1: To find magnitude of Resultant R
R = ΣFy = - 70 + 100 + 50
= 50 N
Step 2: To find ΣMo
Taking moment about point “O”
𝛴𝑀 = 100
= 394 N
Step 3: Applying Varignon’s theorem
Step 4: Position
Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
33
Find the resultant of following force system and also find the
equivalent force and couple at point A of the same force
system shown in fig.
Case I : To find resultant of force system
To find magnitude of Resultant R
70 + 100 + 50 – 86-34 + 90
= 50 N (↑)
To find ΣMo
Taking moment about point “O”
100 × 1.5 + 50 × 3.5 − 86 × 6.5 − 34
= 394 N-m (↺)
Applying Varignon’s theorem,
𝛴𝑀 = 𝑅 × 𝑑
𝑑 =
𝛴𝑀
𝑅
=
394
50
= 7.88 𝑚
Position of the resultant force,
Find the resultant of following force system and also find the
equivalent force and couple at point A of the same force
× 8 + 90 × 10

34. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM
Case II : To find
Step 1: To find magnitude of Resultant R
R = ΣF = - 70 + 100 + 50
= 50 N
Step 2: To find ΣM
Taking moment about point “A”
𝛴𝑀 = 70
= 219
Step 3: Position of the equivalent force and couple,
2. Find the resultant of
w.r.t. point B.
Solution Step 1: To find magnitude of Resultant R
Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
34
: To find equivalent force and couple at point A
To find magnitude of Resultant R
70 + 100 + 50 – 86 - 34 + 90
= 50 N (↑)
To find ΣMA
Taking moment about point “A”
70 × 3.5 − 100 × 2 − 86 × 3 − 34 × 4
219 N-m (↺)
Position of the equivalent force and couple,
Find the resultant of given active forces as shown in fig.
w.r.t. point B.
To find magnitude of Resultant R
equivalent force and couple at point A
4.5 + 90 × 6.5
Position of the equivalent force and couple,
given active forces as shown in fig.

35. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
35
R = ΣF = 100 + 200 -150
= 150 N (→)
Step 2: To find ΣMB
Taking moment about point “B”
𝛴𝑀 = 150 + 100 × 5 − 150 × 3.5 + 200 × 1.5
= 425 N-m = 425 N-m (↻)
Step 3: Applying Varignon’s theorem,
𝛴𝑀 = 𝑅 × ℎ
ℎ =
𝛴𝑀
𝑅
=
425
150
= 2.83 𝑚
Step 4: Position of the resultant force w.r.t point B,
3. Find the resultant of given active forces as shown in fig. and
show its position w.r.t. point A.

36. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
36
Solution Step 1: To find magnitude of Resultant R
Here we will consider AC as x-axis
R = ΣF = - 50 + 60 – 70 + 80 – 90
= - 70 N
= 70 N
Step 2: To find ΣMA
Taking moment about point “A”
𝛴𝑀 = −60 × 3 + 70 × 6 − 80 × 7.5 + 90 × 9
= 450 N-m = 450 N-m (↻)
Step 3: Applying Varignon’s theorem,
𝛴𝑀 = 𝑅 × 𝑑
𝑑 =
𝛴𝑀
𝑅
=
450
70
= 6.429 𝑚
Step 4: Position of the resultant force w.r.t point A,
4. Determine the resultant of the parallel forces as shown in fig
and locate it w.r.t. O, radius is 1m.

37. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
37
Solution Step 1: To draw a FBD of given fig
For 80 N force and 150 N force
sin 𝜃 =
𝑂𝑝𝑝
𝐻𝑦𝑝𝑜
sin 30° =
𝑥
1
x1 = 0.5 m
For 100 N force
sin 60° =
𝑥
1
x2 = 0.866 m
For 50 N force
sin 45° =
𝑥
1

38. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
38
x3 = 0.707 m
Step 2: To find magnitude of Resultant R
R = ΣF = - 100 – 80 + 150 - 50
= 80 N (←)
Step 3: To find ΣMo
Taking moment about point “O”
𝛴𝑀 = 100 × 0.866 + 80 × 0.5 + 150 × 0.5 − 50 × 0.707
= 166.25 N-m (↺)
Step 3: Applying Varignon’s theorem,
𝛴𝑀 = 𝑅 × 𝑑
𝑑 =
𝛴𝑀
𝑅
=
166.25
80
= 2.078 𝑚
Step 4: Position of the resultant force,
5. A part roof truss is acted by wind and other forces as shown
in figure. All the forces form a parallel force system and are
perpendicular to portion AB of the truss. Find the resultant
of the force and its location w.r.t. hinge A.

39. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
39
(Ans : R = 1000 N and d = 0)
6. Replace the force system acting on a bar as shown in fig. by a
single force.
(Ans : R = 80 N and d = 2.375 m)

40. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
40
Type 6: Problems on Resultant of general
force system using Method of Resolution
 STEPWISE PROCEDURE OF METHOD OF RESOLUTION:
1. Resolve all forces horizontally and find the algebraic sum of all
the horizontal components (i.e., ΣFx)
2. Resolve all forces vertically and find the algebraic sum of all
the vertical components (i.e., ΣFy).
3. Find the magnitude of Resultant R
The resultant R of the given forces will be given by the
equation:
𝑹 = (𝚺𝐅𝐱𝟐
) + (𝚺𝐅𝐲𝟐
)
4. Find direction θ. The resultant force will be inclined at an
angle θ, with the horizontal, such that
tan𝜃 =
ΣFy
ΣFx
5. Find ΣMo. Take the algebraic sum moment of forces about a
point (say O) considering proper sign convention.
(+𝒗𝒆 ↻ −𝑪𝒍𝒐𝒄𝒌𝒘𝒊𝒔𝒆) ( −𝒗𝒆 ↺ −𝒂𝒏𝒕𝒊𝒄𝒍𝒐𝒄𝒌𝒘𝒊𝒔𝒆)
6. Apply Varignon’s theorem,
I. 𝜮𝑴𝒐 = 𝑹 × 𝒅,Where d = perpendicular distance between
line of action of R and reference point O. OR

41. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
41
II. 𝜮𝑴𝒐 = 𝜮𝑭𝒙 × 𝒚, Where y = distance between point O and
the intersection of line of action of resultant R with y-axis.
OR
III. 𝜮𝑴𝒐 = 𝜮𝑭𝒚 × 𝒙, Where y = distance between point O and
the intersection of line of action of resultant R with x-axis.
7. Position of the resultant with respect to point O.
Depending upon the sign of ΣFx, ΣFy and ΣMo any one possible
position of R among the following eight may arise.
1
2

42. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
42
3
4
5
6

43. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
43
7
8

44. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
44
1. Replace the system of forces and couple shown in fig. by a
single force couple system at A.
Solution Step 1: Resolving all the forces horizontally (ΣFx)
𝛴𝐹𝑥 = −100 cos 36.87° − 75
= 155 N (←)
Step 2: Resolving all the forces vertically (ΣFy)
𝛴𝐹𝑦 = −200 + 30 − 100 sin 36.87°
= 210 N (↓)
Step 3: Magnitude of the resultant force,
𝑹 = (𝚺𝐅𝐱𝟐
) + (𝚺𝐅𝐲𝟐
)
𝑅 = (155) + (210)
𝑅 = 261 𝑁
Step 4: Direction of the resultant force,
𝐭𝐚𝐧 𝜽 =
𝚺𝐅𝐲
𝚺𝐅𝐱
tan 𝜃 =
210
155
𝜃 = 53.57°
Step 5: Find ΣMA
𝛴𝑀 = 50 × 2 + 80 − 100 sin 36.87°

45. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
45
2. Replace the system of forces shown in fig. by a single force.
Solution General Calculations:
tan 𝜃1 =
𝑂𝑝𝑝
𝐴𝑑𝑗
=
2
1.5
1) 𝜃1 = tan
.
= 53.13°
2) 𝜃2 = tan = 33.69°
3) 𝜃3 = tan = 18.44°
4) 𝜃4 = tan
.
= 53.13°
5) 𝜃5 = tan
.
= 50.13°
Step 1: Resolving all the forces horizontally (ΣFx)
𝛴𝐹𝑥 = 65 cos 53.13° + 140 cos 33.69 − 90 cos 18.44
− 100 cos 53.13 + 50 cos 50.13
= 42.12 N (→)
Step 2: Resolving all the forces vertically (ΣFy)
𝛴𝐹𝑦 = −65 sin 53.13° + 140 sin 33.69 − 90 sin 18.44
+ 100 sin 53.13 − 50 sin 50.13
= 38.78 N (↑)

46. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
46
Step 3: Magnitude of the resultant force,
𝑹 = (𝚺𝐅𝐱𝟐
) + (𝚺𝐅𝐲𝟐
)
𝑅 = (42.12) + (38.78)
𝑅 = 57.25 𝑁
Step 4: Direction of the resultant force,
𝐭𝐚𝐧 𝜽 =
𝚺𝐅𝐲
𝚺𝐅𝐱
tan 𝜃 =
38.78
42.12
𝜃 = 42.64°
Step 5: To find ƩMo,
Ʃ𝑀𝑜 = 65 cos 53.13 × 3
− 140 sin 33.39 × 1.5
− 90 cos 18.44 × 3
+ 90 sin 18.44 × 4.5
− 100 cos 53.13 × 1
− 100 sin 53.13 × 6
+ 50 cos 50.19 × 3 + 50 sin 50.19 × 6

47. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM
Step 6: Apply Varignon’s theorem
Step 7: Position of Resultant
3. Find the resultant of the force system shown in fig. and
replace it by a single force and couple system at A.
Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
47
Ʃ𝑀𝑜 = 341.03 𝑁. 𝑚 ↺
Apply Varignon’s theorem
Ʃ𝑀𝑜 = Ʃfy x X
𝑥 =
341.03
38.78
= 8.79𝑚
Position of Resultant
Find the resultant of the force system shown in fig. and
replace it by a single force and couple system at A.
↺
Find the resultant of the force system shown in fig. and
replace it by a single force and couple system at A.

48. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
48
Solution Step 1: Resolving all the forces horizontally (ΣFx)
𝛴𝐹𝑥 = 100 cos 40 + 85 cos 50 + 70 sin 40
= 176.24 N (→)
Step 2: Resolving all the forces vertically (ΣFy)
𝛴𝐹𝑦 = 100 sin 40 − 85 sin 50 − 90 − 70cos 40
= 144.46 N (↓)
Step 3: Magnitude of the resultant force,
𝑹 = (𝚺𝐅𝐱𝟐
) + (𝚺𝐅𝐲𝟐
)
𝑅 = (176.24) + (144.46)
𝑅 = 227.88 𝑁
Step 4: Direction of the resultant force,
𝐭𝐚𝐧 𝜽 =
𝚺𝐅𝐲
𝚺𝐅𝐱
tan 𝜃 =
144.46
176.24
𝜃 = 39.34°
Step 5: Find ΣMO
𝛴𝑀 = −100 cos 40 × 4
+ 100 sin 40 × 4
+ 85 cos 50 × 5 − 85 sin 50 × 2 + 90 × 3 + 175 − 150
ΣMO = 388.65 N. m (↻)
Step 6: Apply Varignon’s theorem
R x d
𝑑 =
388.65
227.88
= 1.70 𝑚

49. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM
Step 7: Position of Resultant R W.r.t. O
Step 8: Find ΣM
𝛴𝑀 = −175
−
−
−
Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
49
ƩFx . y
𝑦 =
388.65
176.24
= 2.20𝑚
ƩFy . x
𝑥 =
388.65
144.46
= 2.69 𝑚
Position of Resultant R W.r.t. O
Find ΣMA
+ 150
− 70 sin 40 × 4
− 70 cos 40 × 4
− 85 sin 50 × 2 − 85 cos 50 × 9 − 90
ΣMA = 1671.43 N. m (↺
90 × 7
↺)

50. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM
4. Find the resultant of the force
2.5 m.
Solution Free Body Dia.
Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
50
Find the resultant of the force system shown in fig Radius =
Free Body Dia.
system shown in fig Radius =

51. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
51
Step 1: Resolving all the forces horizontally (ΣFx)
𝛴𝐹𝑥 = 84 cos 40 − 55 cos 35 + 79 cos 60 + 50
= 108.79 N (→)
Step 2: Resolving all the forces vertically (ΣFy)
𝛴𝐹𝑦 = −84 sin 40 − 55 sin 35 − 79 sin 60 + 123 − 60
= 90.96 N (↓)
Step 3: Magnitude of the resultant force,
𝑹 = (𝚺𝐅𝐱𝟐
) + (𝚺𝐅𝐲𝟐
)
𝑅 = (108.79) + (90.96)
𝑅 = 141.80 𝑁
Step 4: Direction of the resultant force,
𝐭𝐚𝐧 𝜽 =
𝚺𝐅𝐲
𝚺𝐅𝐱
tan 𝜃 =
90.96
108.79
𝜃 = 39.89°

52. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
52
Step 5: Find ΣMO
𝛴𝑀 = 84 ∗ 2.5 − 123 ∗ 2.5 + 55 ∗ 2.5 − 79 ∗ 2.5 + 50
∗ 2.5 cos 40 − 60 ∗ 2.5 sin 40
ΣMO = 158.16 N. m (↺)
Step 6: Apply Varignon’s theorem
R x d
𝑑 =
158.16
141.80
= 1.12 𝑚
Step 7: Position of Resultant R W.r.t. O
Assignment 3
Q1. A triangular plate ABC is subjected to four coplanar
forces as shown in fig. Find the resultant completely and
locate its position with respect to A.

53. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM
Ans: R = 12.71 KN, θ=86.48°,
Hint:
Fig.1. FBD
Q2. Determine the resultant of the following force system
Ans: R = 199.64 N & θ=4.10 °
Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
53
R = 12.71 KN, θ=86.48°, ƩMA= 77.66 KN.m and x= 6.12 m
Fig.1. FBD Fig.2. Position
Determine the resultant of the following force system
R = 199.64 N & θ=4.10 °
= 77.66 KN.m and x= 6.12 m
Fig.2. Position
Determine the resultant of the following force system

54. Prepared By: Prof. V.V. Nalawade , Assistant Professor, MGM University
54
Q3. The resultant of the three pulls applied through the
three chain attached to bracket is θ as shown in fig.
Determine the magnitude and θ of the resultant
Ans: R = 623.24 N & θ =75.4 °
Q.4. State and Explain a) Parallelogram Law B) Varignon’s
Theorem
Q.5. Classify the force System