BTrees - Great alternative to Red Black, AVL and other BSTs

CS 6213 –
Advanced
Data
Structures
Lecture 4
BTREES
AN EXCELLENT DATA
STRUCTURE FOR DISK ACCESS

 Instructor
Prof. Amrinder Arora
amrinder@gwu.edu
Please copy TA on emails
Please feel free to call as well
 TA
Iswarya Parupudi
iswarya2291@gwmail.gwu.edu
L4 - BTrees CS 6213 - Advanced Data Structures - Arora 2
LOGISTICS

CS 6213
Basics
Record /
Struct
Arrays / Linked
Lists / Stacks
/ Queues
Graphs / Trees
/ BSTs
Advanced
Trie, B-Tree
Splay Trees
R-Trees
Heaps and PQs
Union Find

 T.K.Prasad @ Purdue University
 Prof. Sin-Min Lee @ San Jose State University
 Rada Mihalcea @ University of North Texas
CREDITS

 Eventually you run out of RAM
 Plus, you need persistent storage
 Storing information on disk requires different
approach to efficiency
 Access time includes seek time and rotational delay
 Assuming that a disk spins at 3600 RPM, one
revolution occurs in 1/60 of a second, or 16.7ms.
 In other words, one disk access takes about the
same time as 200,000 instructions
MOTIVATION FOR B-TREES

 Assume that we use an AVL tree to store about 20 million
records
 log2 20,000,000 is about 24
 24 operations in terms of time is very small (4 GHz CPU,
etc).
 Normal data operation should take a few nanoseconds.
 However, a large binary tree in a file will cause lots of
different disk accesses
 24 * 16.7ms = 0.4 seconds
 Suddenly database query response time in seconds starts
making sense.
MOTIVATION FOR B-TREES (CONT.)

 We can’t improve the theoretical log n lower bound
on search for a binary tree
 But, the solution is to use more branches and thus
reduce the height of the tree!
 As branching increases, depth decreases
MOTIVATION FOR B-TREES (CONT.)

 Invented by Bayer and McCreight in 1972
 (Bayer also invented Red Black Trees)
 Definition is in terms of “order”, which is not always
clear, and different researchers mean different
things, but concepts remain the same.
 We will use Knuth’s terminology, where order
represents the maximum number of children.
B-TREES

 B-tree of order m (where m is an odd number) is an
m-way search tree, where keys partition the keys in
the children in the fashion of a search tree, with
following additional constraints:
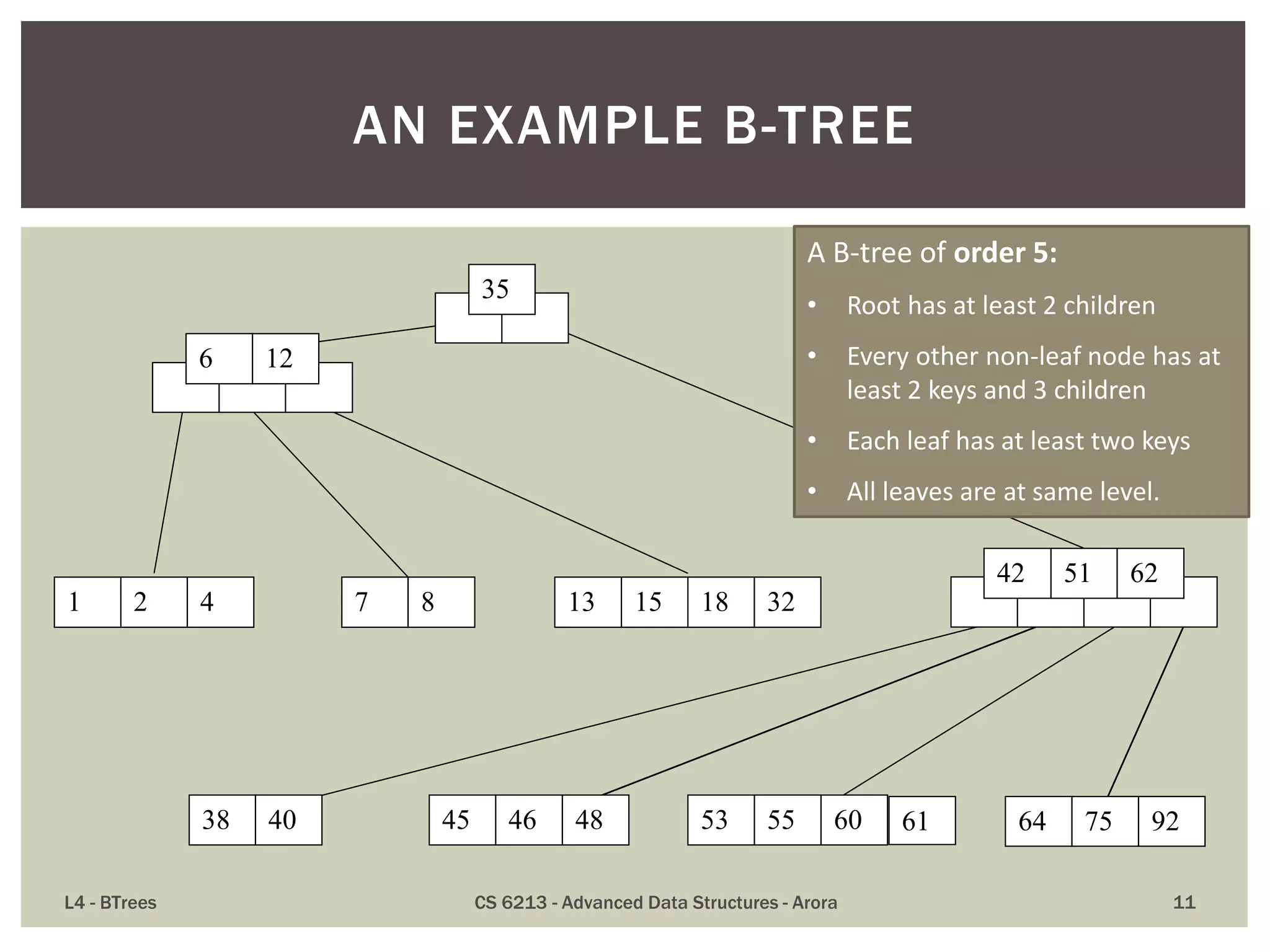
1. [max] a node contains up to m – 1 keys and up to m children
(Actual number of keys is one less than the number of
children)
2. [min] all non-root nodes contain at least (m-1)/2 keys
3. [leaf level] all leaves are on the same level
4. [root] the root is either a leaf node, or it has at least two
children
B-TREE: DEFINITION

 While as per Knuth’s definition B-Tree of order 5 is a
tree where a node has a maximum of 5 children
nodes, the same tree may be defined as a [2,4] tree
in the sense that for any node, the number of keys is
between 2 and 4, both inclusive.
B-TREE: ALTERNATE DEFINITION

AN EXAMPLE B-TREE
51 6242
6 12
35
55 60 7564 9245
1 2 4 7 8 13 15 18 32
38 40 46 48 53
A B-tree of order 5:
• Root has at least 2 children
• Every other non-leaf node has at
least 2 keys and 3 children
• Each leaf has at least two keys
• All leaves are at same level.
61

 Different approach compared AVL Trees
 Don’t insert a new leaf, rather split the root and add
a new level above the root. This automatically
increases the height of ALL the leaves by one.
KEEPING THE HEIGHT SAME

 We want to construct a B-tree of order 5
 Suppose we start with an empty B-tree and keys
arrive in the following order: 1 12 8 2 25 5 14 28
17 7 52 16 48 68 3 26 29 53 55 45
 The first four items go into the root:
CONSTRUCTING A B-TREE
1 2 8 12

 To put the fifth item in the root would violate
constraint 1 (max)
 Therefore, when 25 arrives, we pick the middle key
to make a new root
CONSTRUCTING A B-TREE (CONT.)
1 2
8
12 25

 6, 14, 28 get added to the leaf nodes
1 2
8
12 146 25 28

 Adding 17 to the right leaf node would violate
constraint 1 (max), so we promote the middle key
(17) to the root and split the leaf
8 17
12 14 25 281 2 6

 7, 52, 16, 48 get added to the leaf nodes
8 17
12 14 25 281 2 6 16 48 527

 Adding 68 causes us to split the right most leaf,
promoting 48 to the root, and adding 3 causes us to
split the left most leaf, promoting 3 to the root; 26,
29, 53, 55 then go into the leaves
3 8 17 48
52 53 55 6825 26 28 291 2 6 7 12 14 16

 Adding 45 causes a split of
 But we observe that this does not cause the problem
of leaves at different heights.
 Rather, we promote 28 to go to the root.
 However, root is already full:
 So, this causes the root to split: 17 then becomes the
new root.
25 26 28 29
3 8 17 48

17
3 8 28 48
1 2 6 7 12 14 16 52 53 55 6825 26 29 45

 Attempt to insert the new key into a leaf
 If this would result in that leaf becoming too big,
split the leaf into two, promoting the middle key to
the leaf’s parent
 If this would result in the parent becoming too big,
split the parent into two, promoting the middle key
 This strategy might have to be repeated all the way
to the top
 If necessary, the root is split in two and the middle
key is promoted to a new root, making the tree one
level higher
SUMMARY: INSERTING INTO A B-TREE

 Insert the following keys to a 5-way B-tree:
 13, 27, 51, 3, 2, 14, 28, 1, 7, 71, 89, 37, 41, 44
EXERCISE IN INSERTING A B-TREE

REMOVAL FROM A B-TREE – 4
SCENARIOS
Scenario 1:
• Key to delete is a leaf node, and removing it doesn’t
cause that leaf node to have too few keys, then simply
remove the key to be deleted.
Scenario 2:
• Key to delete is not in a leaf and moving its successor or
predecessor does not cause the leaf node to have too
few keys. (We are guaranteed by the nature of a B-tree
that its predecessor or successor will be in a leaf.)
Scenario 3:
• Key to delete is a leaf node, but deleting it will have the
leaf to have too few keys, and we can borrow from an
adjacent leaf node.
Scenario 4:
• Key to delete is a leaf node, but deleting it will have the
leaf to have too few keys, and we cannot borrow from an
adjacent leaf node. Then the lacking leaf and one of its
neighbours can be combined with their shared parent
(the opposite of promoting a key) and the new leaf will
have the correct number of keys; if this step leave the
parent with too few keys then we repeat the process up
to the root itself, if required

SIMPLE LEAF DELETION
12 29 52
2 7 9 15 22 56 69 7231 43
We want to delete 2:
Since there are enough
keys in the node, we can just
delete it
Scenario1

SIMPLE LEAF DELETION (CONT.)
12 29 52
7 9 15 22 56 69 7231 43
That’s it, we deleted 2 and we
are done.
Scenario1

SIMPLE NON-LEAF DELETION
12 29 52
7 9 15 22 56 69 7231 43
Borrow the predecessor
or (in this case) successor
We want to delete 52. So, we
delete it, and see that the
successor can be moved up.
Scenario2

SIMPLE NON-LEAF DELETION (CONT.)
12 29 56
7 9 15 22 69 7231 43
Done. 52 is gone. 56
promoted to the non-leaf
node. Leaf nodes are still
meeting the min constraint.
Scenario2

TOO FEW KEYS IN NODE, BUT WE
CAN BORROW FROM SIBLINGS
12 29
7 9 15 22 695631 43
We want to delete 22 – that will
lead to too few keys in the node
(constraint 2). But we can borrow
from the adjacent node (via the
root).
Demote root key and
promote leaf key
Scenario3

TOO FEW KEYS IN NODE, BUT WE CAN
BORROW FROM SIBLINGS (CONT.)
12
297 9 15
31
695643
Done – 22 is gone. 29 came
down from the parent node, and
31 has gone up from the right
adjacent node.
Scenario3

TOO FEW KEYS IN NODE AND ITS
SIBLINGS
12 29 56
7 9 15 22 69 7231 43
We want to delete 72. This will lead to too few keys in
this node (constraint 2). We cannot borrow from the
adjacent sibling as it only has two. So, we need to
combine 31, 43, 56 and 69 into one node.
Scenario4

TOO FEW KEYS IN NODE AND ITS
SIBLINGS (CONT.)
12 29
7 9 15 22 695631 43
Done. 72 is gone. 31, 43, 56 and 69
combined into one node.
Scenario4

 The maximum number of items in a B-tree of order m and
height h:
root m – 1
level 1 m(m – 1)
level 2 m2(m – 1)
. . .
level h mh(m – 1)
 So, the total number of items is
(1 + m + m2 + m3 + … + mh)(m – 1) =
[(mh+1 – 1)/ (m – 1)] (m – 1) = mh+1 – 1
 When m = 5 and h = 2 this gives 53 – 1 = 124
ANALYSIS OF B-TREES

 Since there is a lower bound on the number of child
nodes of non-root nodes, a B-Tree is at least 50%
“full”.
 On average it is 75% full.
 The advantage of not being 100% full is that there
are empty spaces for insertions to happen without
going all the way to the root.
ANALYSIS OF B-TREES (CONT.)

 If m = 3, the specific case of B-Tree is called a 2-3
tree.
 For in memory access, 2-3 Tree may be a good
alternative to Red Black or AVL Tree.
2-3 TREES

 For small in-memory data structures, BSTs, Arrays, Hashmaps,
etc. work well.
 When we exceed the size of the RAM, or for persistence
reasons, the problem becomes quite different.
 The cost of each disc transfer is high but doesn't depend much on the
amount of data transferred, especially if adjacent items are transferred
 B-Trees are a great alternative (and very highly used) data
structure for disk accesses
 A B-Tree of order m allows each node to have from m/2 up to m children.
 There is flexibility that allows for gaps. This flexibility allows: (i) some
new elements to be stored in leaves with no other changes, and (ii) some
elements to be deleted easily without changes propagating to root
 If we use a B-tree of order 101, a B-tree of order 101 and height 3 can
hold 1014 – 1 items (approximately 100 million) and any item can be
accessed with 3 disc reads (assuming we hold the root in memory)
CONCLUSIONS &
RECAP OF CENTRAL IDEA

 If we take m = 3, we get a 2-3 tree, in which non-leaf
nodes have two or three children (i.e., one or two
keys)
 B-Trees are always balanced (since the leaves are all at the
same level), so 2-3 trees make a good type of balanced tree
CONCLUSIONS AND RECAP (CONT.)

BTrees - Great alternative to Red Black, AVL and other BSTs

More Related Content

What's hot

Viewers also liked

Similar to BTrees - Great alternative to Red Black, AVL and other BSTs

More from Amrinder Arora

Recently uploaded

BTrees - Great alternative to Red Black, AVL and other BSTs