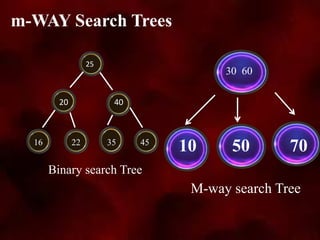
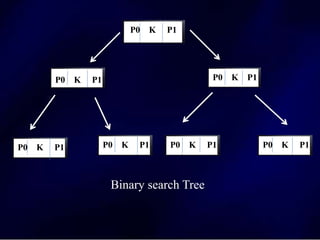
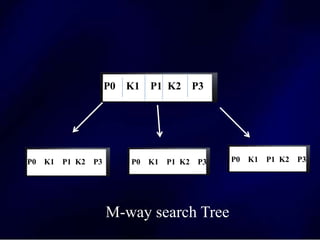
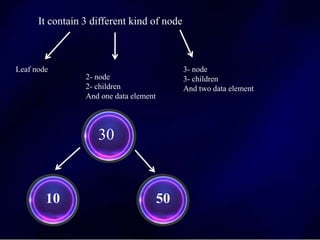
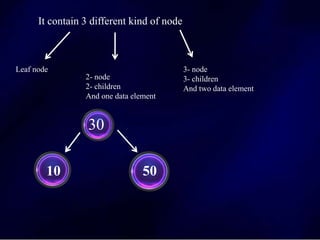
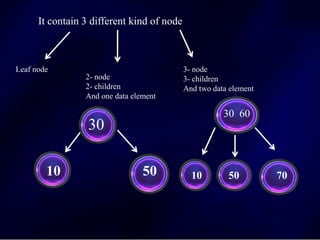
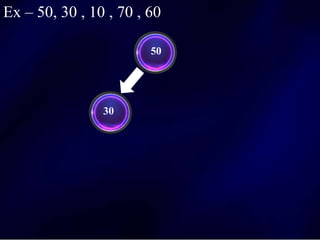
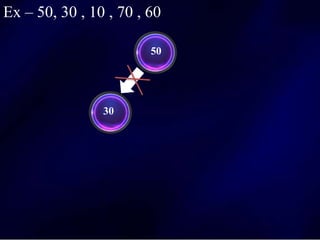
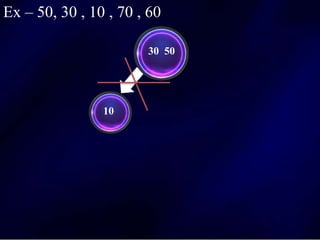
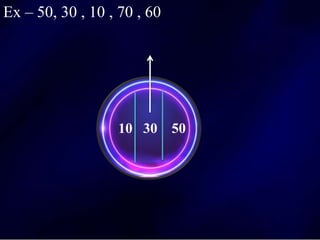
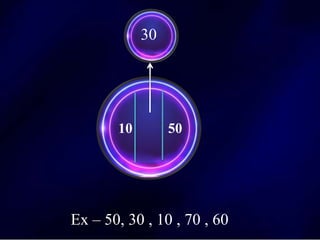
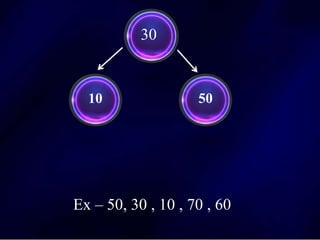
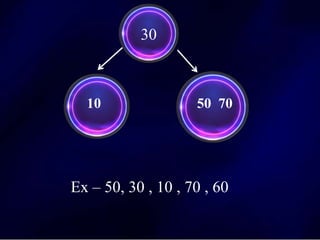
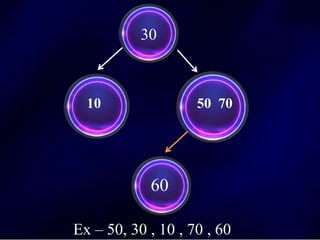
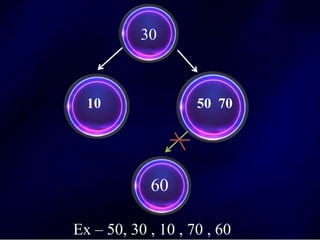
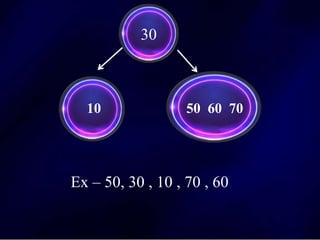
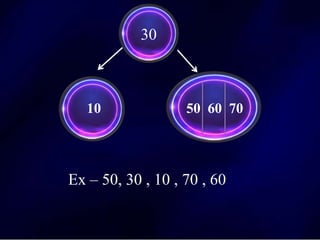
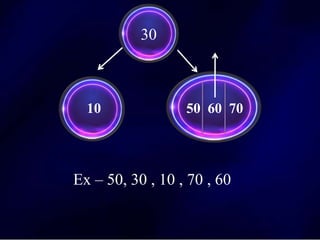
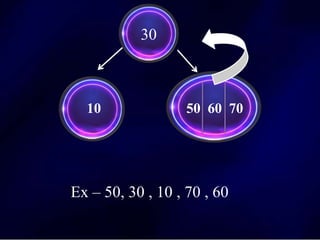
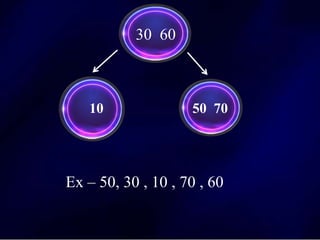
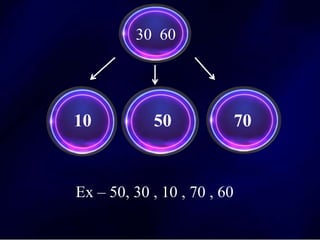
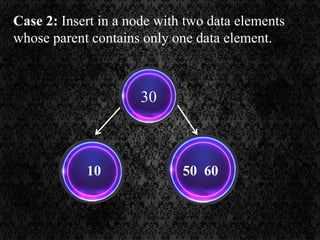
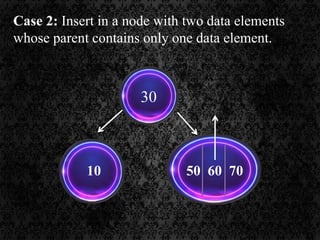
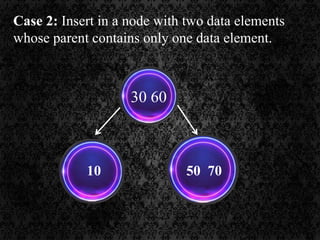
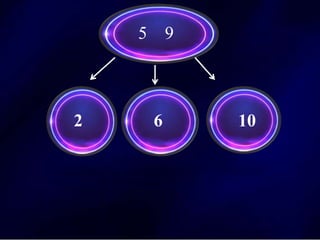
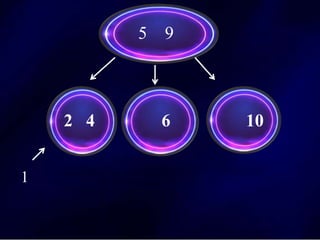
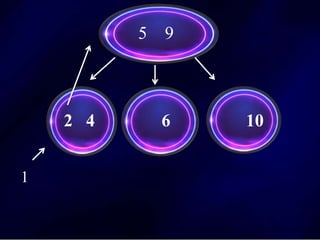
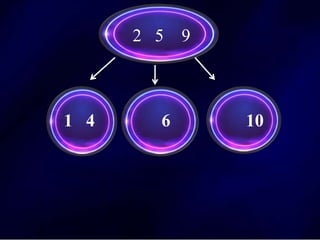
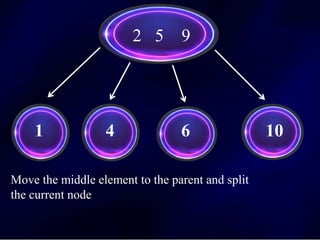
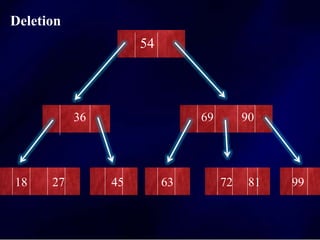
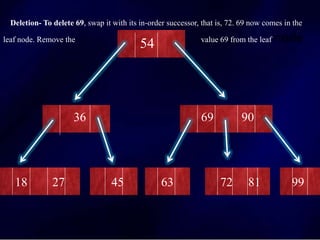
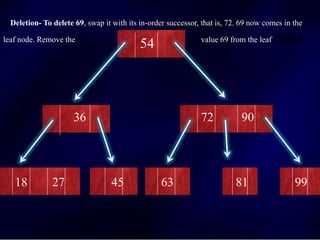
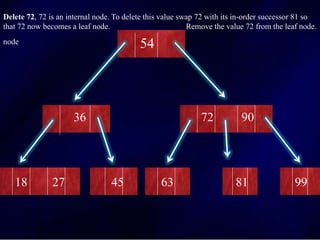
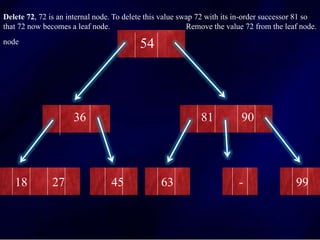
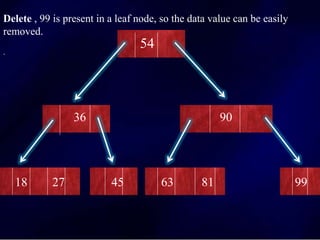
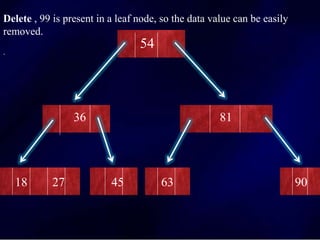
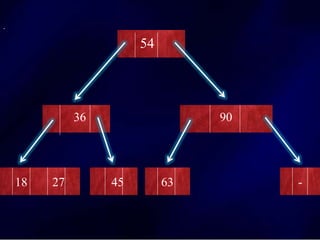
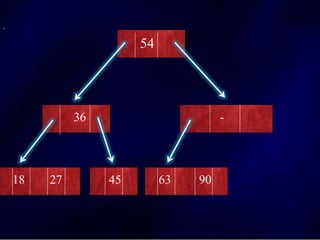
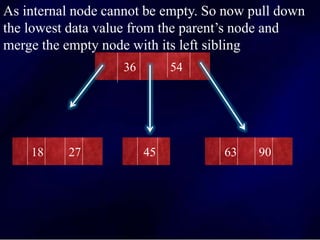
The document discusses multi-way search trees, specifically m-way search trees, which generalize binary search trees by allowing multiple children per node for efficient data searching and sorting. It highlights the characteristics of two common types: 2-3 trees and B-trees, detailing their properties, insertion, and deletion processes. The document provides examples and explanations of how these trees function and their advantages over binary search trees.

1. Submitted By
Ujjwal matoliya
Atal Bihari Vajpayee Vishwavidyalaya
Department of Computer Science and Information

2. It stand for multi-way search tree
m-WAY Search Trees

3. It stand for multi-way search tree
Multi-way search trees are a generalized version
of binary trees
m-WAY Search Trees

4. It stand for multi-way search tree
Multi-way search trees are a generalized version
of binary trees
That allow for efficient data searching and sorting
m-WAY Search Trees

5. It stand for multi-way search tree
Multi-way search trees are a generalized version
of binary trees
That allow for efficient data searching and sorting
In contrast to binary search trees, which can only
have two children per node
m-WAY Search Trees

6. It stand for multi-way search tree
Multi-way search trees are a generalized version
of binary trees
That allow for efficient data searching and sorting
In contrast to binary search trees, which can only
have two children per node
Multi-way search trees can have multiple children
per node
m-WAY Search Trees

7. m-WAY Search Trees
25
20 40
16 22 35 45

8. m-WAY Search Trees
25
20 40
16 22 35 45
Binary search Tree

9. m-WAY Search Trees
25
20 40
16 22 35 45
Binary search Tree
10 50 70
30 60
M-way search Tree

10. P0 K P1
P0 K P1 P0 K P1
P0 K P1 P0 K P1 P0 K P1 P0 K P1
Binary search Tree

11. P0 K1 P1 K2 P3
P0 K1 P1 K2 P3 P0 K1 P1 K2 P3
P0 K1 P1 K2 P3
M-way search Tree

12. K=

13. K= KEY

14. K= KEY = Element

15. K= KEY = Element
P=

16. K= KEY = Element
P= Pointer

17. K= KEY = Element
P= Pointer = a variable that stores the memory address of
another variable as its value

18. K= KEY = Element
P= Pointer = a variable that stores the memory address of
another variable as its value
P0 K1 P1 K2 P3

19. K= KEY = Element
P= Pointer = a variable that stores the memory address of
another variable as its value
P0 K1 P1 K2 P3 - - - - -

20. K= KEY = Element
P= Pointer = a variable that stores the memory address of
another variable as its value
P0 K1 P1 K2 P3 - - - - - K m-1

21. K= KEY = Element
P= Pointer = a variable that stores the memory address of
another variable as its value
P0 K1 P1 K2 P3 - - - - - K m-1 P m

22. K= KEY = Element
P= Pointer = a variable that stores the memory address of
another variable as its value
P0 K1 P1 K2 P3 - - - - - K m-1 P m-1

23. Types of Multi-way Search Trees

24. Types of Multi-way Search Trees
There are several types of multi-way search
trees, each with unique features and use
cases.
The two common types are

25. Types of Multi-way Search Trees
There are several types of multi-way search
trees, each with unique features and use
cases.
The two common types are
2-3 Tree and B-Tree.

26. 2-3 Trees
2-3 trees are the data structure same as trees,
but it has some different properties like any
node can have either single value or double
value. So, there are two types of nodes in 2-3
trees:

27. 2-3 Trees
Properties of 2-3 tree
Nodes with two children are called 2-nodes. The 2-
nodes have one data value and two children
Nodes with three children are called 3-nodes. The 3-
nodes have two data values and three children.
Data is stored in sorted order.
It is a balanced tree.
All the leaf nodes are at same level.
Each node can either be leaf, 2 node, or 3 node.
Always insertion is done at leaf.

28. 2-3 Trees
2-3 trees are the data structure same as trees,
but it has some different properties like any
node can have either single value or double
value. So, there are two types of nodes in 2-3
trees:
It contain 3 different kind of node

29. 2-3 Trees
2-3 trees are the data structure same as trees,
but it has some different properties like any
node can have either single value or double
value. So, there are two types of nodes in 2-3
trees:
It contain 3 different kind of node
Leaf node

30. 2-3 Trees
2-3 trees are the data structure same as trees,
but it has some different properties like any
node can have either single value or double
value. So, there are two types of nodes in 2-3
trees:
It contain 3 different kind of node
Leaf node 2- node

31. 2-3 Trees
2-3 trees are the data structure same as trees,
but it has some different properties like any
node can have either single value or double
value. So, there are two types of nodes in 2-3
trees:
It contain 3 different kind of node
Leaf node 2- node
2- children
And one data element

32. 2-3 Trees
2-3 trees are the data structure same as trees,
but it has some different properties like any
node can have either single value or double
value. So, there are two types of nodes in 2-3
trees:
It contain 3 different kind of node
Leaf node 2- node
2- children
And one data element
3- node

33. 2-3 Trees
2-3 trees are the data structure same as trees,
but it has some different properties like any
node can have either single value or double
value. So, there are two types of nodes in 2-3
trees:
It contain 3 different kind of node
Leaf node 2- node
2- children
And one data element
3- node
3- children
And two data element

34. It contain 3 different kind of node
Leaf node
2- node
2- children
And one data element
3- node
3- children
And two data element
10 50
30

35. It contain 3 different kind of node
Leaf node
2- node
2- children
And one data element
3- node
3- children
And two data element
10 50
30

36. It contain 3 different kind of node
Leaf node
2- node
2- children
And one data element
3- node
3- children
And two data element
10 50
30
10 50 70
30 60

38. Ex – 50, 30 , 10 , 70 , 60

39. 50
Ex – 50, 30 , 10 , 70 , 60

40. 50
30
Ex – 50, 30 , 10 , 70 , 60

41. 50
30
Ex – 50, 30 , 10 , 70 , 60

42. 30 50
Ex – 50, 30 , 10 , 70 , 60

43. 50
10
30 50
Ex – 50, 30 , 10 , 70 , 60

44. 10 30 50
Ex – 50, 30 , 10 , 70 , 60

45. 10 50
30
Ex – 50, 30 , 10 , 70 , 60

46. 10 50
30
Ex – 50, 30 , 10 , 70 , 60

47. 10 50 70
30
Ex – 50, 30 , 10 , 70 , 60

48. 10 50 70
30
60
Ex – 50, 30 , 10 , 70 , 60

49. 10 50 70
30
60
Ex – 50, 30 , 10 , 70 , 60

50. 10 50 60 70
30
Ex – 50, 30 , 10 , 70 , 60

51. 10 50 60 70
30
Ex – 50, 30 , 10 , 70 , 60

52. 10 50 60 70
30
Ex – 50, 30 , 10 , 70 , 60

53. 10 50 60 70
30
Ex – 50, 30 , 10 , 70 , 60

54. 10 50 70
30 60
Ex – 50, 30 , 10 , 70 , 60

55. 10 50 70
30 60
Ex – 50, 30 , 10 , 70 , 60

56. Search:
If T is empty, return False (key cannot be found in
the tree).
If current node contains data value which is equal
to K, return True.
If we reach the leaf-node and it doesn’t contain the
required key value K, return False.
Recursive Calls:
If K < currentNode.leftVal, we explore the left
subtree of the current node.
Else if currentNode.leftVal < K <
currentNode.rightVal, we explore the middle subtree
of the current node.
Else if K > currentNode.rightVal, we explore the
right subtree of the current node.

57. Insertion:

58. Insertion:
There are 3 possible cases in insertion which have
been discussed below:

59. Insertion:
There are 3 possible cases in insertion which have
been discussed below:
Case 1: Insert in a node with only one data
element

60. Insertion:
There are 3 possible cases in insertion which have
been discussed below:
Case 1: Insert in a node with only one data element
Case 2: Insert in a node with two data elements
whose parent contains only one data element.

61. Case 2: Insert in a node with two data elements
whose parent contains only one data element.
10 50 60
30

62. Case 2: Insert in a node with two data elements
whose parent contains only one data element.
10 50 60 70
30

63. Case 2: Insert in a node with two data elements
whose parent contains only one data element.
10 50 70
30 60

64. Insertion:
There are 3 possible cases in insertion which have
been discussed below:
Case 1: Insert in a node with only one data element
Case 2: Insert in a node with two data elements
whose parent contains only one data element.
Case 3: Insert in a node with two data elements
whose parent also contains two data elements.

65. 2 6 10
5 9

66. 2 4 6 10
5 9
1

67. 2 4 6 10
5 9
1

68. 1 4 6 10
2 5 9

69. 1 4 6 10
2 5 9
Move the middle element to the parent and split
the current node

70. Deletion
To delete a value, it is replaced by its in-order
successor and then removed.
If a node is left with less than one data value then
two nodes must be merged together.
If a node becomes empty after deleting a value, it is
then merged with another node.

71. Deletion
54
36 69 90
18 27 45 63 72 81 99

72. Deletion- To delete 69, swap it with its in-order successor, that is, 72. 69 now comes in the
leaf node. Remove the value 69 from the leaf node.
54
36 69 90
18 27 45 63 72 81 99

73. Deletion- To delete 69, swap it with its in-order successor, that is, 72. 69 now comes in the
leaf node. Remove the value 69 from the leaf node.
54
36 72 90
18 27 45 63 81 99

74. Delete 72, 72 is an internal node. To delete this value swap 72 with its in-order successor 81 so
that 72 now becomes a leaf node. Remove the value 72 from the leaf node.
node. 54
36 72 90
18 27 45 63 81 99

75. Delete 72, 72 is an internal node. To delete this value swap 72 with its in-order successor 81 so
that 72 now becomes a leaf node. Remove the value 72 from the leaf node.
node. 54
36 81 90
18 27 45 63 - 99

76. Now there is a leaf node that has less than 1 data value
thereby violating the property of a 2-3 tree. So the
node must be merged.
To merge the node, pull down the lowest data value in
the parent’s node and merge it with its left sibling.

77. Delete , 99 is present in a leaf node, so the data value can be easily
removed.
.
54
36 90
18 27 45 63 81 99

78. Delete , 99 is present in a leaf node, so the data value can be easily
removed.
.
54
36 81
18 27 45 63 90

79. delete 81, 81 is an internal node. To delete this value
swap 81 with its in-order successor 90 so that 81 now
becomes a leaf node. Remove the value 81 from the
leaf node.
Now there is a leaf node that has less than 1 data
value, thereby violating the property of a 2-3 tree. So
the node must be merged. To merge the node, pull
down the lowest data value in the parent’s node and
merge it with its left sibling.

80. .
54
36 90
18 27 45 63 -

81. .
54
36 -
18 27 45 63 90

82. .
36 54
18 27 45 63 90
As internal node cannot be empty. So now pull down
the lowest data value from the parent’s node and
merge the empty node with its left sibling