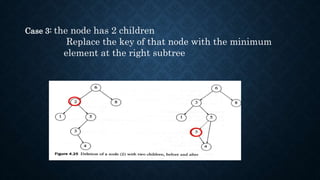
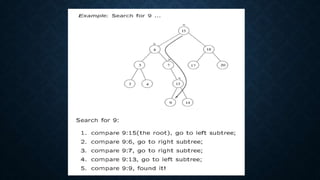
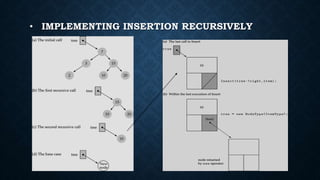
The document describes binary search trees (BST), detailing their properties, structure, and algorithms for searching, insertion, and deletion. It highlights how elements in a BST must adhere to specific ordering rules based on their relationship to the root node. Additionally, it discusses the computational complexity of various operations in a BST and its applications in data management and search tasks.

1. BIRLA INSTITUTE OF TECHNOLOGY
MESRA,
JAIPUR CAMPUS
TOPIC:- BINARY SEARCH TREE
NAME:- TARUN TIWARI
ROLL NO.:- MCA/25007/18
CLASS:- MCA 2ND SEM.

2. BINARY SEARCH TREE
• In Binary Search Tree, all the left subtree elements
should be less than root data and all the right
subtree elements should be greater than root data.
This is called binary search tree property.
• This property should be satisfied at every node in
the tree.

3. Examples
Binary
search trees
Not a binary
search tree
5
10
30
2 25 45
5
10
45
2 25 30
5
10
30
2
25
45

4. Data
NODE
LEFT CHILD RIGHT CHILD
Struct node {
int data;
struct node *leftChild;
struct node *rightChild;
};
STRUCTURE OF TREE NODE

5. SEARCHING BINARY SEARCH TREE
Example: Suppose T is the tree being searched:
• If we are searching for 15, then we are done.
• If we are searching for a key < 15, then we should search in the left
subtree.
• If we are searching for a key > 15, then we should search in the
right subtree.

7. BINARY SEARCH TREE ALGORITHM
SearchElement (TREE,VAL)
Step 1: If Tree-> DATA=VAL OR TREE=NULL
RETURN TREE
ELSE
IF VAL < TREE -> DATA
RETURN SearchElement(TREE->LEFT,VAL)
ELSE
RETURN SearchElement(TREE->RIGHT,VAL)
[END OF IF]
[END OF IF]
Step 2 : EXIT

8. INSERTION BINARY SEARCH TREE

9. • IMPLEMENTING INSERTION RECURSIVELY

10. BINARY SEARCH TREE INSERTION
ALGORITHM
INSERT (TREE,VAL)
Step 1: IF TREE= NULL
Allocate memory for TREE
SET TREE -> DATA=VAL
SET TREE ->LEFT = TREE->RIGHT =NULL
ELSE
IF VAL < TREE->DATA
INSERT (TREE->LEFT , VAL)
ELSE
INSERT (TREE->RIGHT , VAL)
[END OF IF]
[END OF IF]
Step 2: EXIT

11. DELETION BINARY SEARCH TREE
Case 1: the node is a leaf Delete it immediately
Case 2: the node has one child
Adjust a pointer from the parent to bypass that
node

12. Case 3: the node has 2 children
Replace the key of that node with the minimum
element at the right subtree

13. COMPLEXITY IN BST
Operation Average Worst Case Best
Case
Search O(log n) O(n) O(1)
Insertion O(log n) O(n) O(1)
Deletion O(log n) O(n) O(1)

14. APPLICATIONS OF BST
• Used in many search applications where data is constantly
entering/leaving, such as the map and set objects in many
languages' libraries.
• Storing a set of names, and being able to lookup based on a prefix
of the name. (Used in internet routers.)
• Storing a path in a graph, and being able to reverse any subsection
of the path in O(log n) time. (Useful in travelling salesman
problems).
• Finding square root of given number
• allows you to do range searches efficiently.

15. THANK YOU