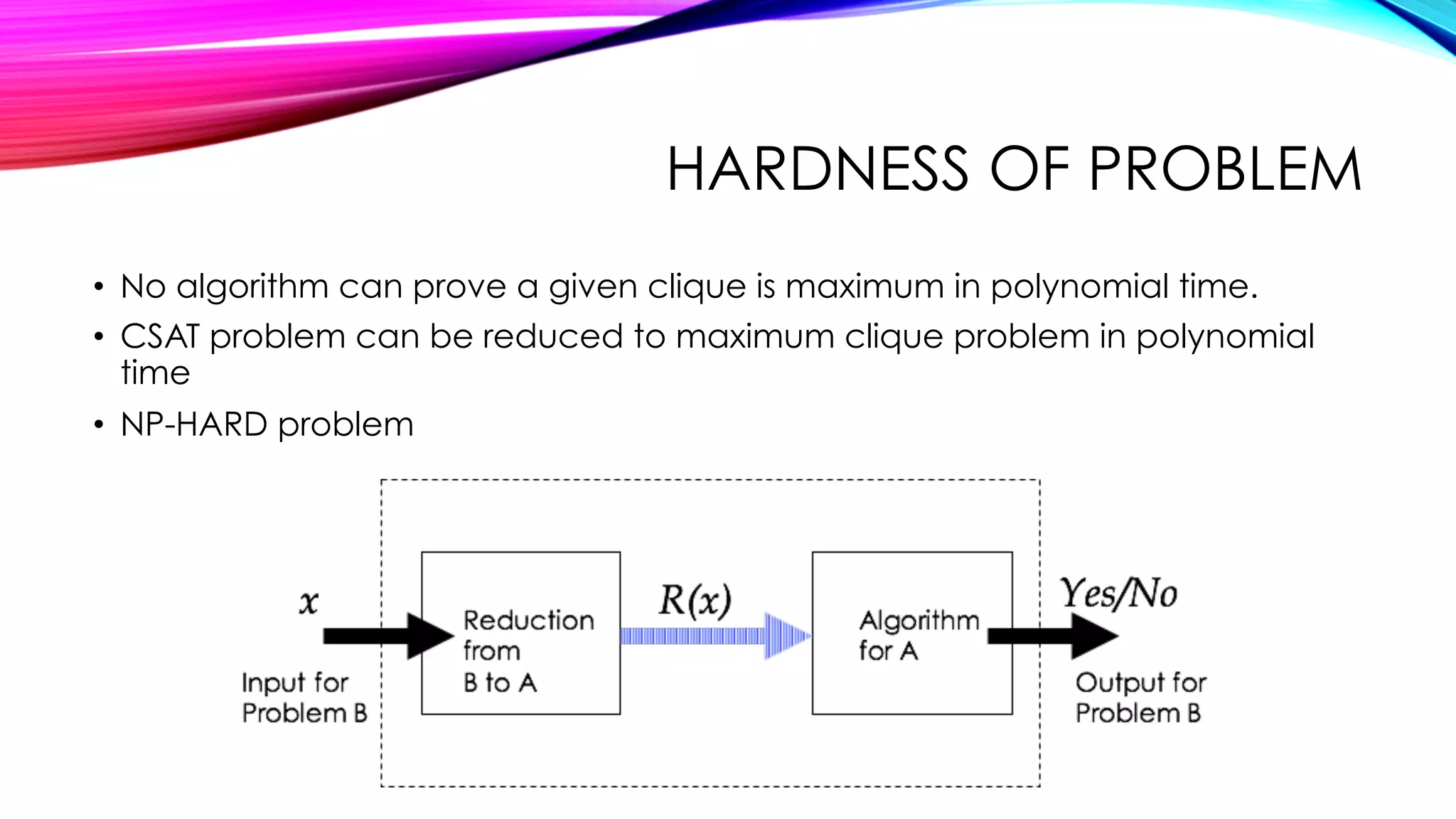
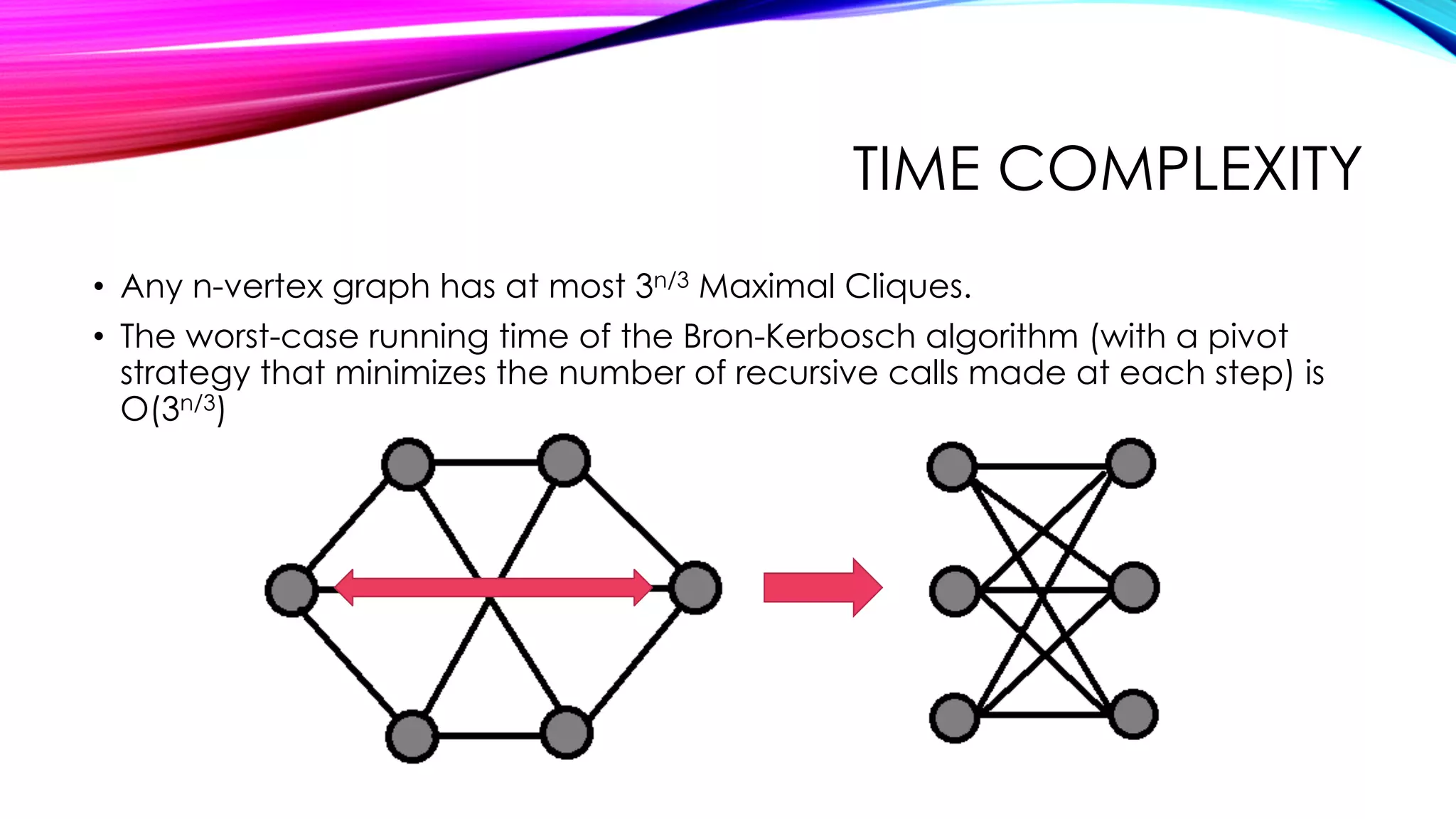
The document discusses the Bron-Kerbosch algorithm for finding maximum cliques in undirected graphs, defining key terms such as clique, maximum clique, and maximal clique. It highlights the NP-hardness of the problem and outlines the algorithm's structure, including its pivot strategy and associated time complexity. Additionally, it provides references for further reading on the topic.

1. BRON-KERBOSCH (BK)
ALGORITHM FOR MAXIMUM
CLIQUE
BY TEAM: WYD
Jun Zhai
Tianhang Qiang
Yizhen JIa

2. PROBLEM DEFINITION
• Clique: A Clique in an undirected graph G = (V,E) is a subset of the vertex set
C ⊆ V, such that for every two vertices in C, there exists an edge connecting
the two.
• Maximum Clique: A Clique of the largest
possible size in a given graph.
• Maximal Clique: A Clique that cannot be
extended by including one more adjacent
vertex.

3. WHY IS THIS PROBLEM IMPORTANT?
• Social Network
• BioInformation
• Computing Chemistry

4. HARDNESS OF PROBLEM
• No algorithm can prove a given clique is maximum in polynomial time.
• CSAT problem can be reduced to maximum clique problem in polynomial
time
• NP-HARD problem

5. BronKerbosch1(R, P, X):
if P and X are both empty:
report R as a maximal clique
for each vertex v in P:
BronKerbosch1(R ⋃ {v}, P ⋂ N(v), X ⋂ N(v))
P := P {v}
X := X ⋃ {v}
BASIC BK ALGORITHM OUTLINE
R: set of vertices that construct
the Maximal Clique
P: set of possible vertices may
be selected
X: set of vertices can not
construct Maximal Clique

6. BASIC BK ALGORITHM OUTLINE

7. BASIC BK ALGORITHM OUTLINE

8. BronKerbosch1(R, P, X):
if P and X are both empty:
report R as a maximal clique
choose a pivot vertex u in P ⋃ X
for each vertex v in P N(u):
BronKerbosch1(R ⋃ {v}, P ⋂ N(v), X ⋂ N(v))
P := P {v}
X := X ⋃ {v}
BK ALGORITHM WITH PIVOT
u: pivot vertex in P
N(u): neighbor vertices of u

9. BK ALGORITHM WITH PIVOT

10. TIME COMPLEXITY
• Any n-vertex graph has at most 3n/3 Maximal Cliques.
• The worst-case running time of the Bron-Kerbosch algorithm (with a pivot
strategy that minimizes the number of recursive calls made at each step) is
O(3n/3)

11. UPPER AND LOWER BOUND
• The upper bound is when the graph had the most maximal cliques. So the
upper bound should be c*3n/3.
• The lower bound is when the graph is a maximal clique. So the lower bound
should be c.

12. REFERENCES
https://en.wikipedia.org/wiki/Bron%E2%80%93Kerbosch_algorithm
https://tuongphuongtn.files.wordpress.com/2012/11/baocaoseminar2012.pdf
https://snap.stanford.edu/class/cs224w-readings/tomita06cliques.pdf
https://www.youtube.com/watch?v=132XR-RLNoY