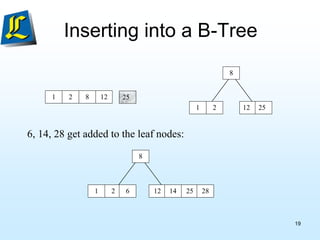
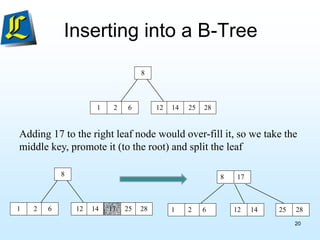
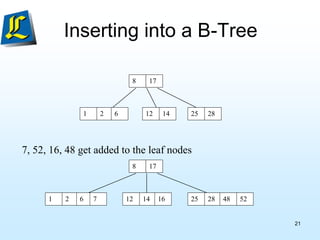
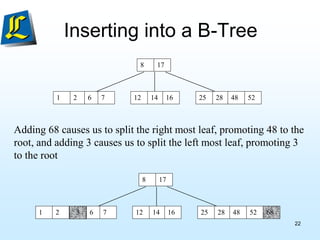
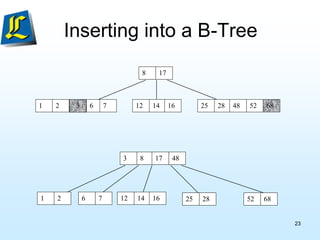
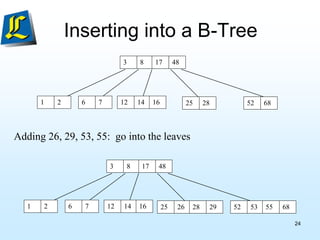
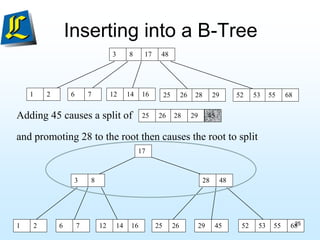
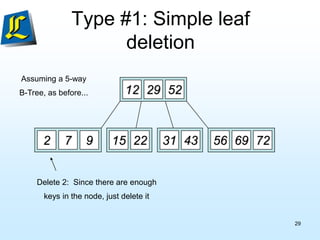
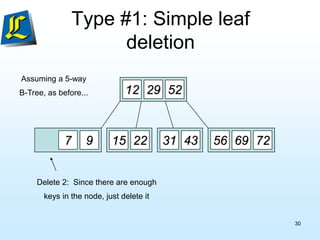
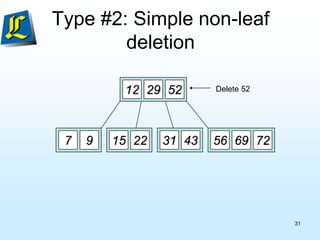
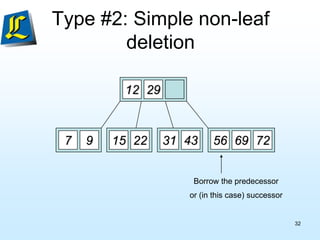
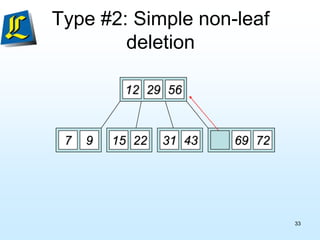
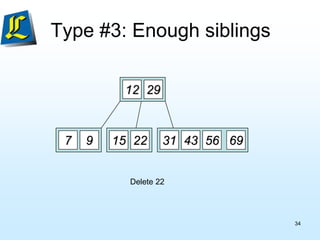
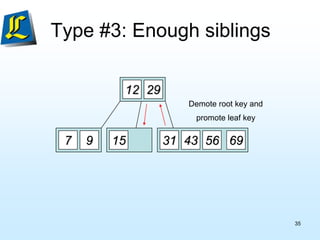
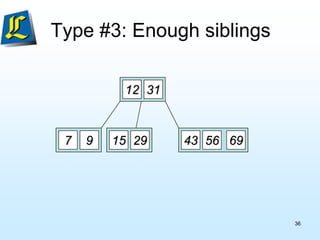
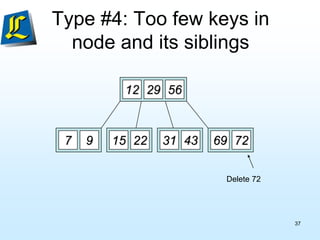
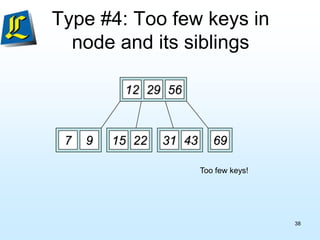
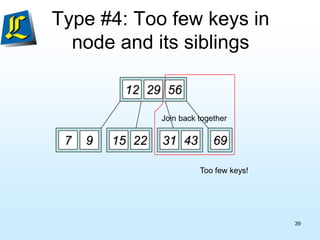
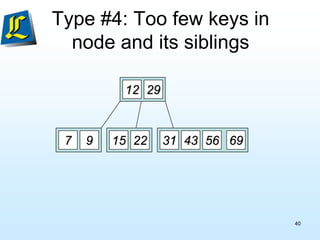
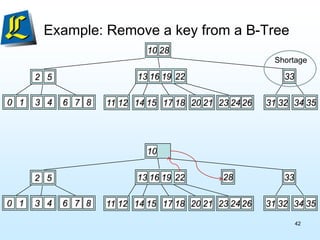
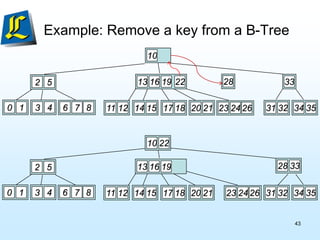
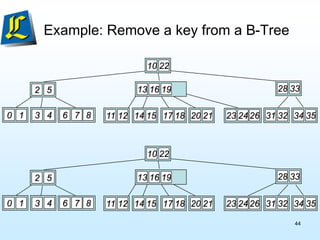
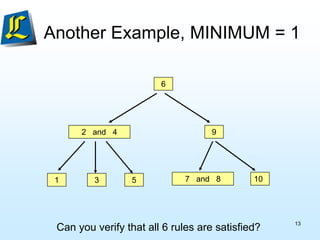
The document discusses B-trees, which are tree data structures used to store large datasets on disk. B-trees allow for faster retrieval of data compared to binary search trees when data exceeds main memory. B-trees differ from binary search trees in that internal nodes can have more than two child nodes and store multiple key-value pairs. The document outlines the rules for B-tree structure and provides examples of inserting and removing elements from a B-tree while maintaining its balanced structure.

1. B-Trees
1

2. World of trees so far…
tree
binary tree
binary
search
tree
heap
balanced
search tree
2

3. World of trees so far…
tree
binary tree
binary
search
tree
heap
n-ary tree
n-ary
search
tree
balanced
search tree
B-Tree
3

4. Motivation for B-Trees
• So far we have assumed that we can store
an entire data structure in main memory
• What if we have so much data that it won’t
fit?
• We will have to use disk storage but when
this happens our time complexity fails
4

5. Motivation for B-Trees
• The problem is that Big-Oh analysis
assumes that all operations take roughly
equal time
• This is not the case when disk access is
involved
• It is worth executing lots of instructions to
avoid a disk access
5

6. 6
Motivation (cont.)
• Assume that we use an AVL tree to store
all the Health card details in CANADA
(about 28 million records)
• We still end up with a very deep tree with
lots of different disk accesses; log2
28,000,000 is about 25
• We know we can’t improve on the log n for
a binary tree

7. 7
Motivation (cont.)
• But, the solution is to use more branches
and thus less height!
• As branching increases, depth decreases
• If we use 10-ary tree:
Log10 28,000,000 ~= 8

8. The B-Tree Basics
• Similar to a binary search tree (BST)
– where the implementation requires the ability to
compare two entries via a less-than operator (<)
• But a B-tree is NOT a BST – in fact it is not even
a binary tree
– B-tree nodes have many (more than two) children
• Another important property
– each node contains more than just a single entry
• Advantages:
– Not too deep
8

9. The B-Tree Rules
• The entries in a B-tree node
– B-tree Rule 1: The root may have as few as
one entry (or 0 entry if no children); every
other node has at least MINIMUM entries
– B-tree Rule 2: The maximum number of
entries in a node is 2* MINIMUM.
– B-tree Rule 3: The entries of each B-tree
node are stored in a partially filled array,
sorted from the smallest to the largest.
9

10. The B-Tree Rules (cont.)
• The subtrees below a B-tree node
– B-tree Rule 4: The number of the subtrees
below a non-leaf node with n entries is always
n+1
– B-tree Rule 5: For any non-leaf node:
• (a). An entry at index i is greater than all the
entries in subtree number i of the node
• (b) An entry at index i is less than all the entries in
subtree number i+1 of the node
10

11. An Example of B-Tree
93 and 107
subtree
number 0 subtree
number 1
subtree
number 2
[0] [1]
each entry < 93
93< each entry < 107 each entry > 107
What kind of traversal can print a sorted list?
11

12. The B-Tree Rules (cont.)
• A B-tree is balanced
– B-tree Rule 6: Every leaf in a B-tree has the
same depth
• This rule ensures that a B-tree is balanced
12

13. Another Example, MINIMUM = 1
Can you verify that all 6 rules are satisfied?
2 and 4
6
7 and 8
9
10
5
3
1
13

14. B-Tree Implementation
public class BTNode
{
Object[] data;
BTNode[] subset;
int dataCount, childCount;
}
14

15. B-Tree Implementation
10 20
3
2
MAXIMUM: data
array size
MINIMUM:
MAXIMUM/2
public class BTNode
{
Object[] data;
BTNode[] subset;
int dataCount, childCount;
}
15

16. B-Tree Capacity
• 1000 element data array (1001 subtree)
• depth 0: 1000
• depth 1: 1000+1001*1000 = 1002000
• depth 2: ~1 Billion
Minimum population of depth 2 subtree:
~500,000 (500*501*2 + 500*2 + 1)
16

17. Inserting into a B-Tree
• Attempt to insert the new key into a leaf
• If this would result in that leaf becoming too big, split the
leaf into two, promoting the middle key to the leaf’s
parent
• If this would result in the parent becoming too big, split
the parent into two, promoting the middle key
• This strategy might have to be repeated all the way to
the top
• If necessary, the root is split in two and the middle key is
promoted to a new root, making the tree one level higher
17

18. • Suppose we start with an empty B-tree and keys arrive
in the following order:1 12 8 2 25 5 14 28 17 7 52
16 48 68 3 26 29 53 55 45
• We want to construct a B-tree of order 5
• The first four items go into the root:
• To put the fifth item in the root would violate condition 5
• Therefore, when 25 arrives, pick the middle key to make
a new root
Inserting into a B-Tree
1 2 8 12 25
18

19. Inserting into a B-Tree
2
1
8
12 25
6, 14, 28 get added to the leaf nodes:
1 2
8
12 14
6 25 28
1 2 8 12 25
19

20. Inserting into a B-Tree
Adding 17 to the right leaf node would over-fill it, so we take the
middle key, promote it (to the root) and split the leaf
8 17
12 14 25 28
1 2 6
1 2
8
12 14
6 25 28
17
1 2
8
12 14
6 25 28
20

21. Inserting into a B-Tree
8 17
12 14 25 28
1 2 6
7, 52, 16, 48 get added to the leaf nodes
8 17
12 14 25 28
1 2 6 16 48 52
7
21

22. Inserting into a B-Tree
Adding 68 causes us to split the right most leaf, promoting 48 to the
root, and adding 3 causes us to split the left most leaf, promoting 3
to the root
8 17
12 14 25 28
1 2 6 16 48 52
7
8 17
12 14 25 28
1 2 6 16 48 52
7 68
3
22

23. 23
Inserting into a B-Tree
8 17
12 14 25 28
1 2 6 16 48 52
7 68
3
3 8 17 48
52 68
25 28
1 2 6 7 12 14 16

24. Inserting into a B-Tree
Adding 26, 29, 53, 55: go into the leaves
3 8 17 48
52 53 55 68
25 26 28 29
1 2 6 7 12 14 16
3 8 17 48
52 68
25 28
1 2 6 7 12 14 16
24

25. Inserting into a B-Tree
17
3 8 28 48
1 2 6 7 12 14 16 52 53 55 68
25 26 29 45
3 8 17 48
52 53 55 68
25 26 28 29
1 2 6 7 12 14 16
Adding 45 causes a split of 25 26 28 29
and promoting 28 to the root then causes the root to split
45
25

26. Sample Exam Question
• Insert the following keys to a 5-way B-tree:
• 3, 7, 9, 23, 45, 1, 5, 14, 25, 24, 13, 11, 8,
19, 4, 31, 35, 56
• Check your approach with a friend and
discuss any differences.
26

27. Removal from a B-Tree
• During insertion, the key always goes into a leaf. For
deletion we wish to remove from a leaf. There are three
possible ways we can do this:
• 1 - If the key is already in a leaf node, and removing it
doesn’t cause that leaf node to have too few keys, then
simply remove the key to be deleted.
• 2 - If the key is not in a leaf then it is guaranteed (by the
nature of a B-tree) that its predecessor or successor will
be in a leaf -- in this case can we delete the key and
promote the predecessor or successor key to the non-
leaf deleted key’s position.
27

28. • If (1) or (2) lead to a leaf node containing less than the minimum
number of keys then we have to look at the siblings immediately
adjacent to the leaf in question:
– 3: if one of them has more than the min’ number of keys then we
can promote one of its keys to the parent and take the parent
key into our lacking leaf
– 4: if neither of them has more than the min’ number of keys then
the lacking leaf and one of its neighbours can be combined with
their shared parent (the opposite of promoting a key) and the
new leaf will have the correct number of keys; if this step leave
the parent with too few keys then we repeat the process up to
the root itself, if required
Removal from a B-tree (2)
28

29. Type #1: Simple leaf
deletion
12 29 52
2 7 9 15 22 56 69 72
31 43
Delete 2: Since there are enough
keys in the node, just delete it
Assuming a 5-way
B-Tree, as before...
29

30. Type #1: Simple leaf
deletion
12 29 52
7 9 15 22 56 69 72
31 43
Delete 2: Since there are enough
keys in the node, just delete it
Assuming a 5-way
B-Tree, as before...
30

31. Type #2: Simple non-leaf
deletion
12 29 52
7 9 15 22 56 69 72
31 43
Delete 52
52
31

32. Type #2: Simple non-leaf
deletion
12 29 52
7 9 15 22 56 69 72
31 43
Borrow the predecessor
or (in this case) successor
32

33. Type #2: Simple non-leaf
deletion
12 29 52
7 9 15 22 56 69 72
31 43
56
33

34. Type #3: Enough siblings
12 29
7 9 15 22 69
56
31 43
Delete 22
34

35. Type #3: Enough siblings
12 29
7 9 15 69
56
31 43
Demote root key and
promote leaf key
35

36. Type #3: Enough siblings
12
29
7 9 15
31
69
56
43
36

37. Type #4: Too few keys in
node and its siblings
12 29 56
7 9 15 22 69 72
31 43
Delete 72
37

38. Type #4: Too few keys in
node and its siblings
Too few keys!
12 29 56
7 9 15 22 69
31 43
38

39. Type #4: Too few keys in
node and its siblings
Too few keys!
12 29 56
7 9 15 22 69
31 43
Join back together
39

40. Type #4: Too few keys in
node and its siblings
12 29
7 9 15 22 69
56
31 43
40

41. Sample Exam Question
• Given 5-way B-tree created by these data (last
exercise):
• 3, 7, 9, 23, 45, 1, 5, 14, 25, 24, 13, 11, 8, 19, 4,
31, 35, 56
• Add these further keys: 2, 6,12
• Delete these keys: 4, 5, 7, 3, 14
• Again, check your approach with a friend and
discuss any differences.
41

42. Example: Remove a key from a B-Tree
42
0 1 17 18
22
19
13 16
14 15 20 21
11 12 26
24
23
3 4 8
7
6 31 32 34 35
2 5 33
10 28
Shortage
0 1 17 18
22
19
13 16
14 15 20 21
11 12 26
24
23
3 4 8
7
6 31 32 34 35
2 5 33
10
28

43. Example: Remove a key from a B-Tree
43
0 1 17 18
22
19
13 16
14 15 20 21
11 12 26
24
23
3 4 8
7
6 31 32 34 35
2 5 33
10
28
34 35
0 1 17 18
19
13 16
14 15 20 21
11 12 26
24
23
3 4 8
7
6 31 32
2 5 28 33
10 22

44. Example: Remove a key from a B-Tree
44
34 35
0 1 17 18
19
13 16
14 15 20 21
11 12 26
24
23
3 4 8
7
6 31 32
2 5 28 33
10 22
34 35
0 1 17 18
19
13 16
14 15 20 21
11 12 26
24
23
3 4 8
7
6 31 32
2 5 28 33
10 22