Uploaded byLittbarski Santos
2-3 Tree, Everything you need to know
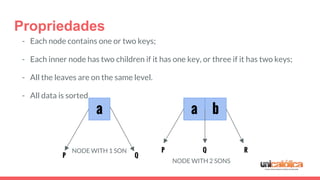
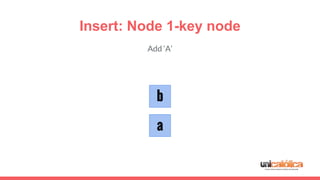
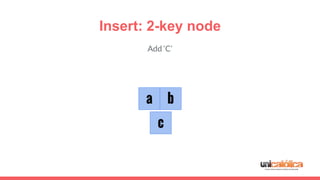
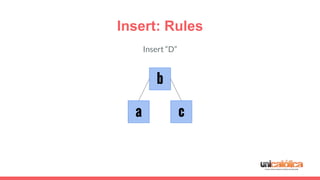
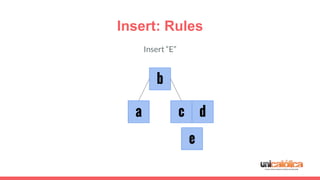
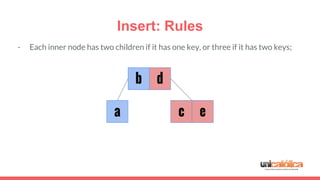
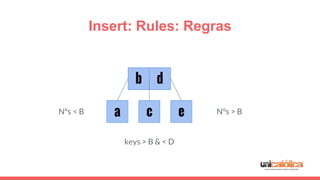
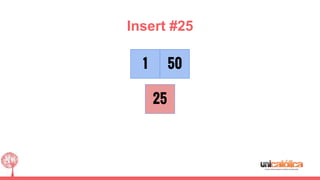
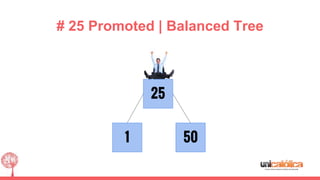
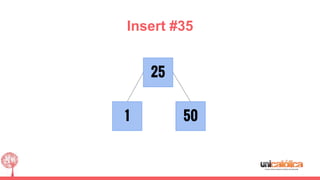
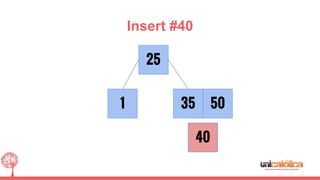
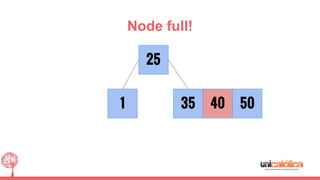
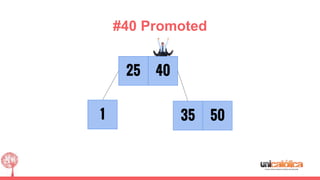
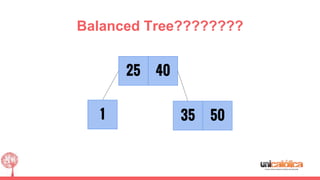
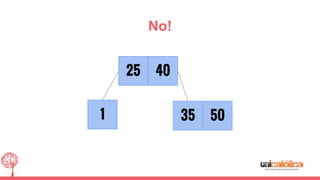
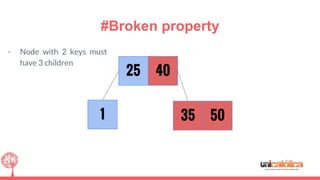
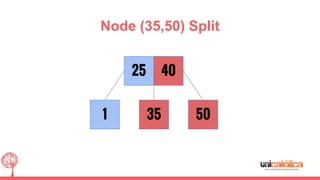
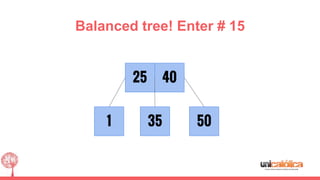
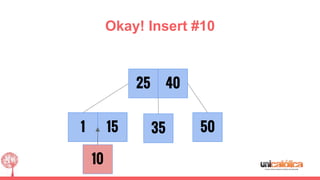
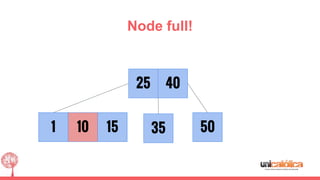
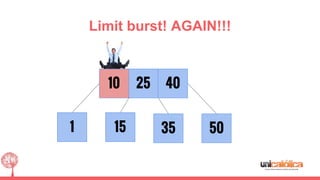
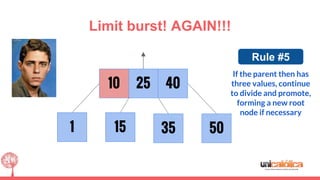
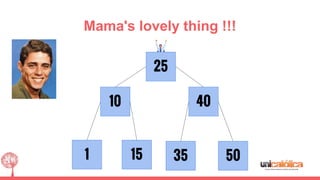
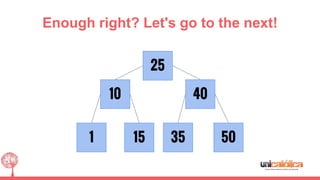
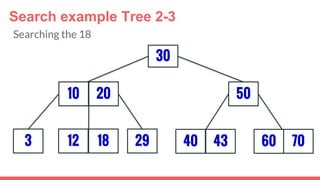
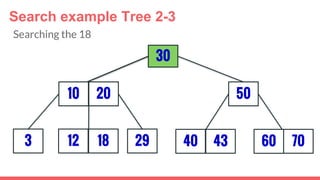
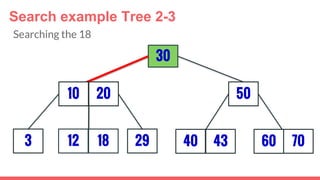
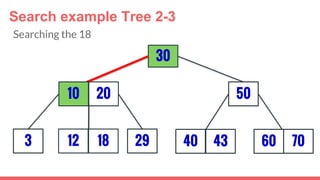
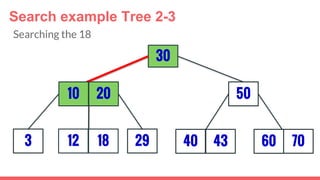
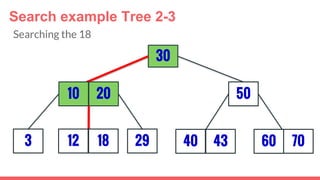
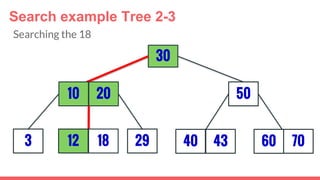
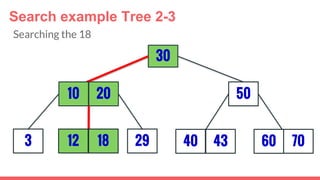
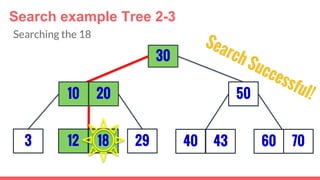
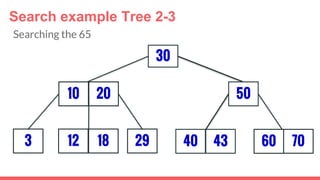
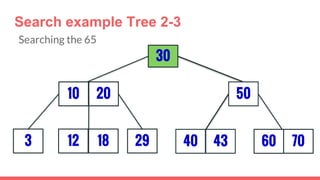
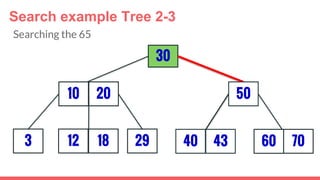
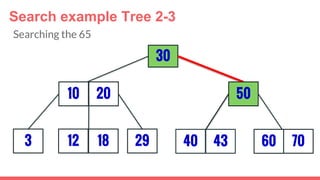
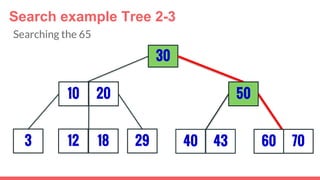
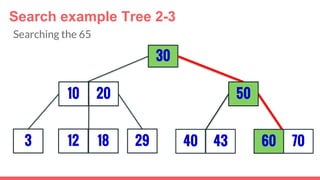
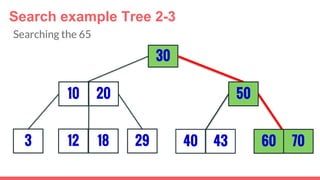
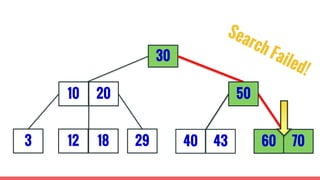
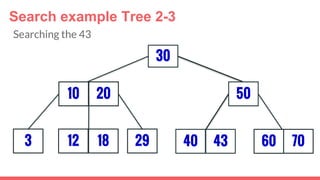
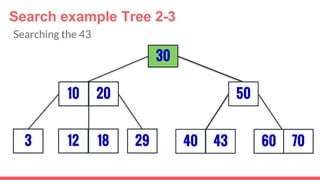
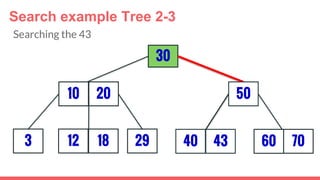
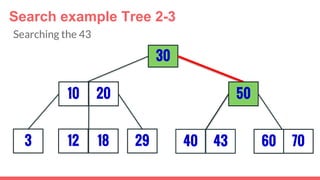
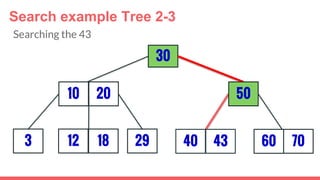
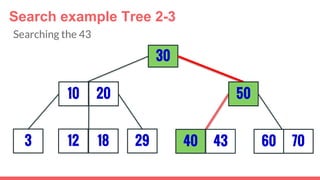
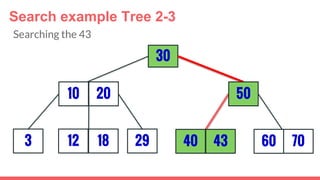
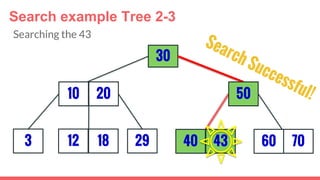
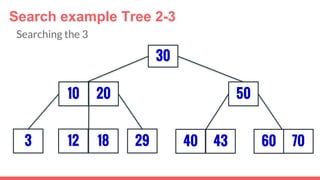
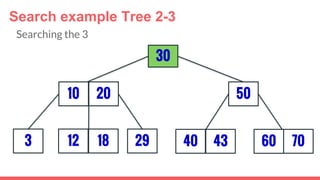
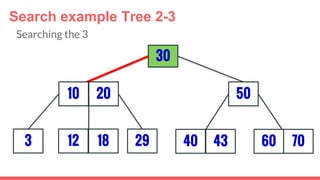
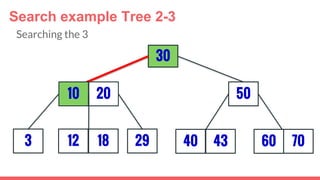
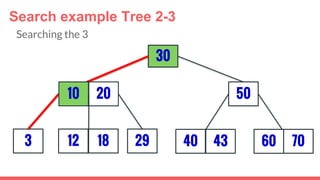
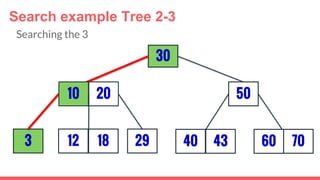
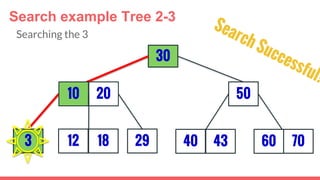
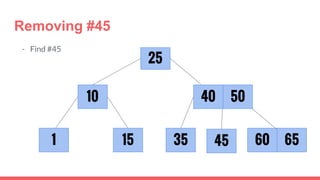
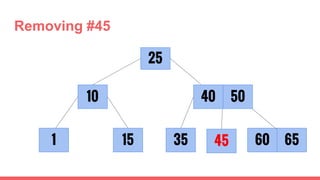
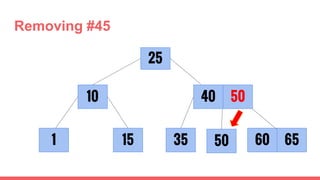
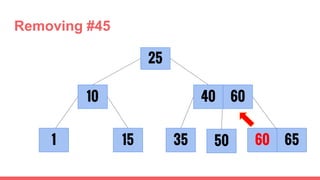
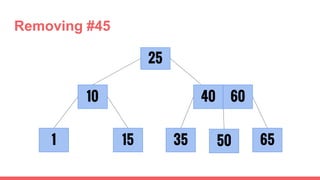
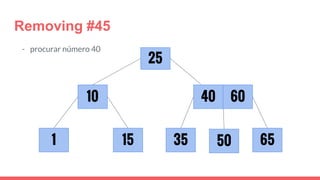
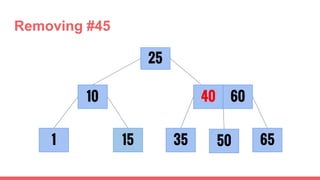
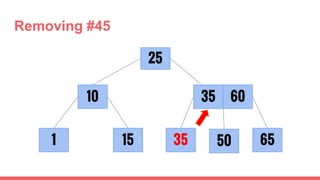
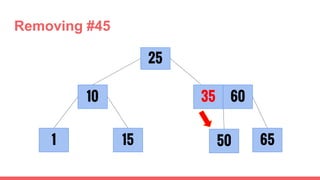
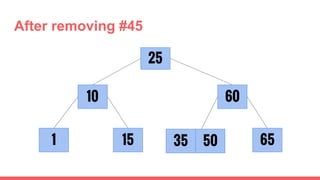
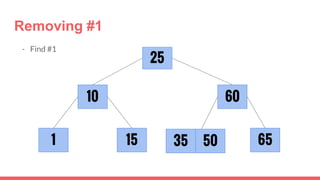
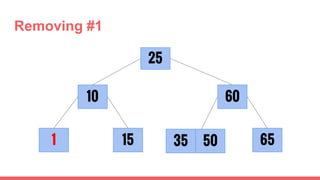
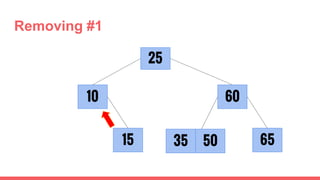
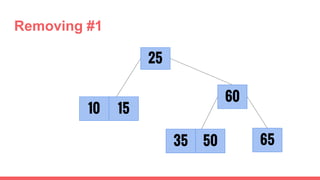
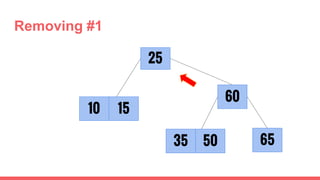
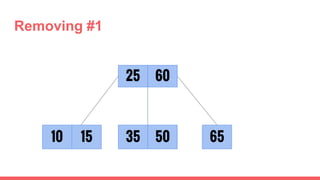
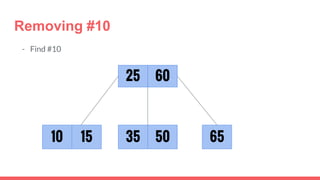
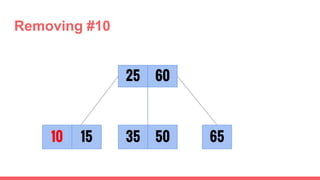
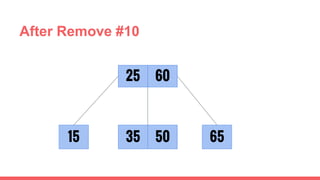
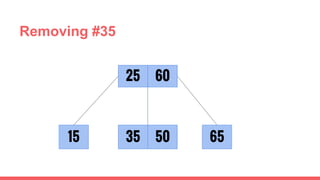
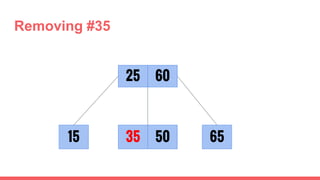
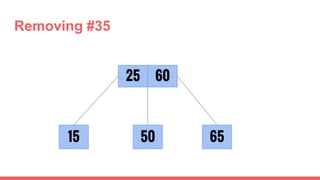
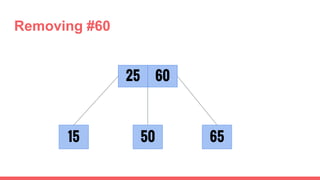
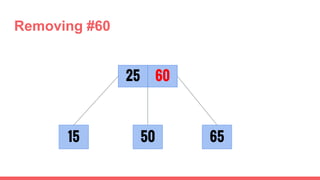
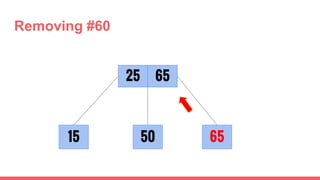
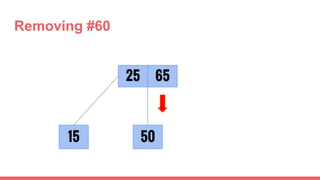
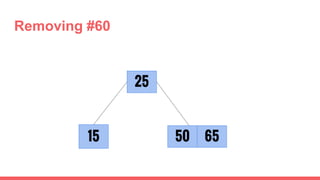
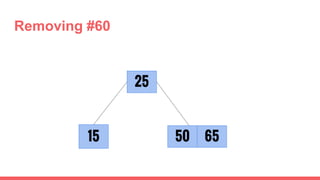
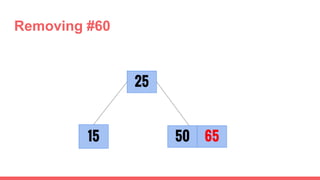
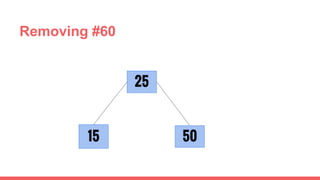
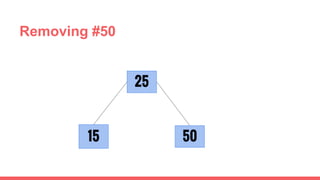
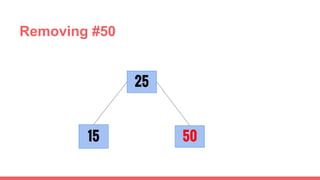
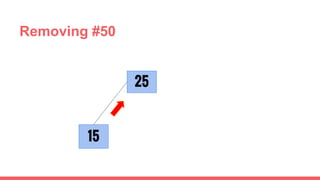
The document discusses 2-3 trees, which are balanced search trees invented by John Hopcroft in 1970. 2-3 trees have the following properties: each node contains 1 or 2 keys, each internal node has 2 children if it has 1 key or 3 children if it has 2 keys, and all leaves are on the same level. The document covers insertion, search, and removal algorithms for 2-3 trees. Insertion may require splitting nodes and promoting keys up the tree to maintain the balanced structure. Search works by recursively traversing the tree to the appropriate child node based on key comparison. Removal is the reverse of insertion, removing nodes by restructuring child pointers or replacing keys.
![Getting Started with Apache Spark: Big Data Made Simple [Free Meetup]](https://cdn.slidesharecdn.com/ss_thumbnails/apachesparkgettingstarted-260203175547-8361bcc3-thumbnail.jpg?width=640&height=640&fit=bounds)
2-3 Tree, Everything you need to know
- 1. 2-3 TREE Estrutura de DadosII Team: Augusto Teixeira Carlos Littbarski Jardel Rodrigues Victor Apuena Professor: Alandson Meireles
- 2. History TREE 2-3 WASTHE FIRST MULTIPATHS TREE, INVENTED BY J. E. HOPCROFT IN 1970. 2-3 trees are an isometry of AA trees, which means that they are equivalent data structures. In other words, for all 2-3 tree, there exists at least one AA tree with data elements in the same order. 2-3 trees are balanced, meaning that each right, center and left subtree contains the same or close to the same amount of data. John E. Hopcroft
- 3. Characteristics - ARE TREESEASY TO SCHEDULE - ARE MULTIVITIES TREES - IT'S NOT A BINARY TREE - TREES 2-3 ARE SIMILAR TO TREES 2-3-4. - 2-3 SAY ABOUT THE QUANTITY OF CHILDREN THAT THE TREE CAN HAVE (AS WELL AS IN 2-3-4) - PERFECTLY BALANCED
- 4. Advantagens Perfectly balanced tree Quicksearch Easy implementation Delayed removal Disadvantages
- 5. Propriedades - Each nodecontains one or two keys; - Each inner node has two children if it has one key, or three if it has two keys; - All the leaves are on the same level. - All data is sorted NODE WITH 1 SON a a b P Q NODE WITH 2 SONS P Q R
- 6.
- 7.
- 8. Insertion: Empty Tree b Ifthe Tree is empty: Create a node and add the value to the node Rule #1
- 9. Insert: Node 1-keynode b Add ‘A’ a
- 10. Insert: Node 1-keynode b Otherwise, locate the node to which the value belongs. If the node has only 1 value, add the value on the node. a Rule #2 Rula #3 Insert key in the node always in an orderly fashion.
- 11. Insert: 2-key node ab c Add ‘C’
- 12. Insert: 2-key node c Ifthe leaf node has more than two values, divide the node and promote the median of the three values for the parent. a b Regra #4 Number of keys burst Promote the median Break the knot and make the call
- 13. Insert: 2-key node ca b Key> BKey < B We with 1 key should always have 2 children
- 14.
- 15.
- 16. Insert: Rules ca b d e Ifthe leaf node has more than two values, divide the node and promote the median of the three values for the parent.Rule #4
- 17. Insert: Rules ca b d e -Each inner node has two children if it has one key, or three if it has two keys;
- 18. Insert: Rules: Regras ca bd e Nºs > BNºs < B keys > B & < D
- 19. Let's see ifwe understand everything?
- 20.
- 21.
- 22.
- 23.
- 24.
- 25. # 25 Promoted| Balanced Tree 1 50 25
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32. #Broken property 1 4025 5035 - Nodewith 2 keys must have 3 children
- 33.
- 34. Balanced tree! Enter# 15 1 4025 5035
- 35. 1 35 25 50 40 Okay! Insert#10 15 10
- 36.
- 37. 1 35 25 50 40 Limit burst!AGAIN!!! 15 10
- 38. 25 4010 If theparent then has three values, continue to divide and promote, forming a new root node if necessary Rule #5 1 35 5015 Limit burst! AGAIN!!!
- 39. 25 40 Mama's lovely thing!!! 10 1 35 5015
- 40. Enough right? Let'sgo to the next! 1 35 25 50 40 15 10
- 41.
- 42. 2-3 Tree ▪ SimpleNode: ▪ Contains a key and two links; A left link to a 2-3 tree that has keys smaller than the node key; And a direct link to a 2- 3 tree that has larger braces;
- 43. 2-3 Tree ▪ DoubleNode: ▪ Contains two keys and three links: a left link to a 2-3 tree that has smaller keys; And a middle link to a 2-3 tree that has keys between the two keys of the node; And a direct link to a 2-3 tree that has larger braces;
- 44. Search in atree 2-3 - It always starts at the root; - If the searched item is not in the root, it identifies the child node of the root in which it can be and continues to this node; - If the item has a value greater than the root, go to the right of the tree, otherwise go to the left; - The process repeats itself until the item is found;
- 45. Search example Tree2-3 3 30 29 5010 20 12 18 40 43 7060 Searching the 18
- 46. 3 30 29 50 12 18 10 20 4043 7060 Search example Tree 2-3 Searching the 18
- 47. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 18
- 48. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 18
- 49. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 18
- 50. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 18
- 51. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 18
- 52. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 18
- 53. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 18
- 54. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 65
- 55. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 65
- 56. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 65
- 57. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 65
- 58. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 65
- 59. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 65
- 60. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 65
- 61. 3 30 29 5010 20 12 1840 43 7060
- 62. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 43
- 63. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 43
- 64. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 43
- 65. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 43
- 66. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 43
- 67. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 43
- 68. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 43
- 69. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 43
- 70. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 3
- 71. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 3
- 72. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 3
- 73. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 3
- 74. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 3
- 75. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 3
- 76. 3 30 29 5010 20 12 1840 43 7060 Search example Tree 2-3 Searching the 3
- 77.
- 78. Removing a tree2-3 - Removing an item from a tree 2-3 is approximately the reverse of the insertion process; - To remove an item, we must first look for it; - If the item to be removed is on a sheet with two items; - We simply exclude it; - We remove it by changing it from the trees;
- 79. Removing #45 - Find#45 1 35 25 60 10 6545 40 50 15
- 80.
- 81.
- 82.
- 83.
- 84. Removing #45 - procurarnúmero 40 1 35 25 15 10 6550 40 60
- 85.
- 86.
- 87.
- 88.
- 89. Removing #1 - Find#1 1 25 15 10 6535 60 50
- 90.
- 91.
- 92.
- 93.
- 94.
- 95. - Find #10 25 106535 60 5015 Removing #10
- 96.
- 97.
- 98.
- 99.
- 100.
- 101.
- 102.
- 103.
- 104.
- 105.
- 106.
- 107.
- 108.
- 109.
- 110.
- 111.
- 112.
- 113.
- 114.
- 115.
- 116. REFERÊNCIAS USP - “Institutode Matemática e Estatística”. Disponível em: https://www.ime.usp.br/~gold/cursos/2002/mac2301/aulas/b-arvore/ LAFORE - ESTRUTURA DE DADOS E ALGORÍTMOS EM JAVA - 2ª EDIÇÃO WIKIPEDIA - https://pt.wikipedia.org/wiki/%C3%81rvore_2-3 Gross, R. Hernández, J. C. Lázaro, R. Dormido, S. Ros (2001). Estructura de Datos y Algoritmos Prentice Hall Ellio B. Koffman Paul A. T. Olfgang (2006) : Objetos, Abstração, Estruturas de dados e projeto usando C++
- 117.