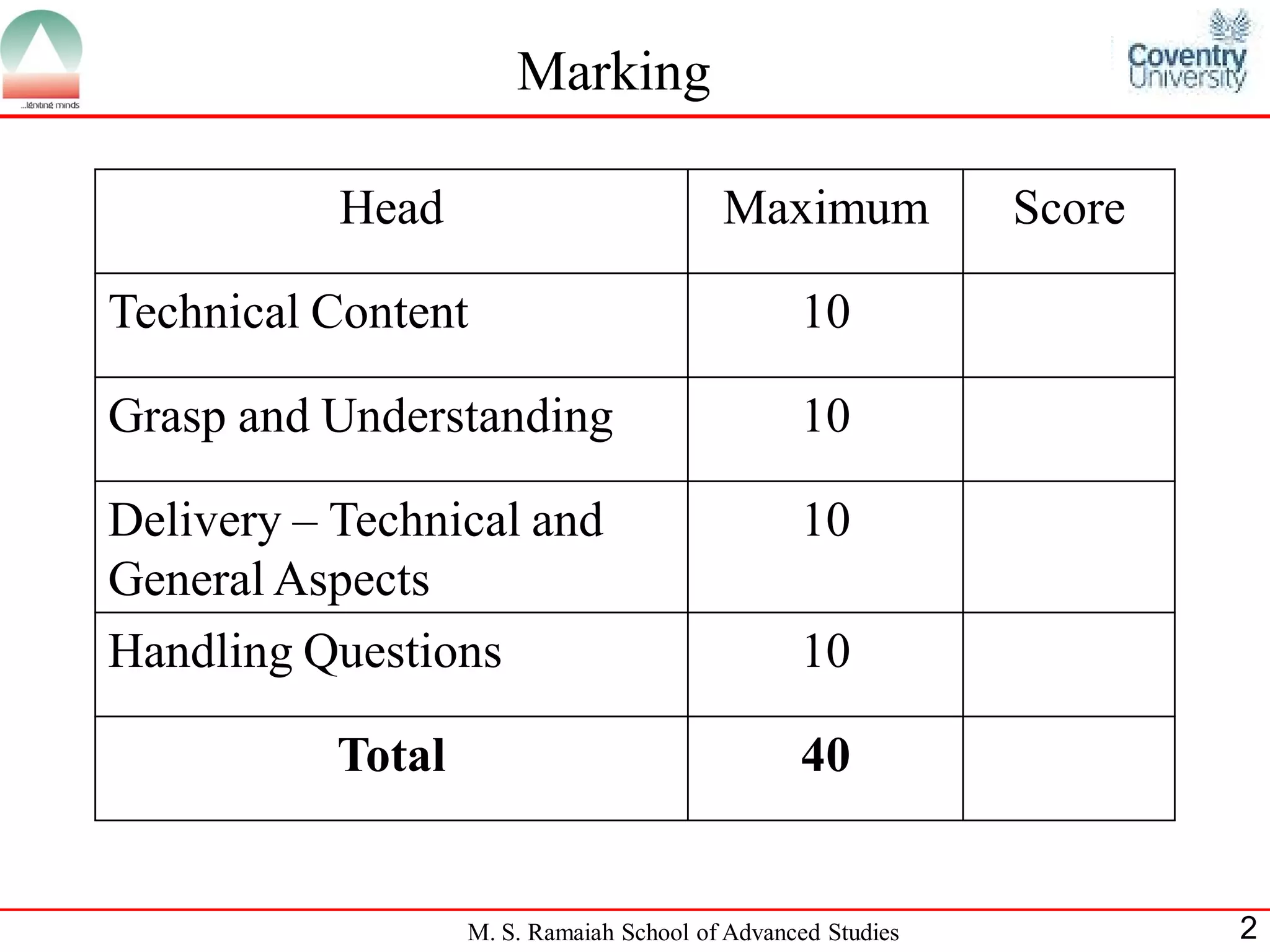
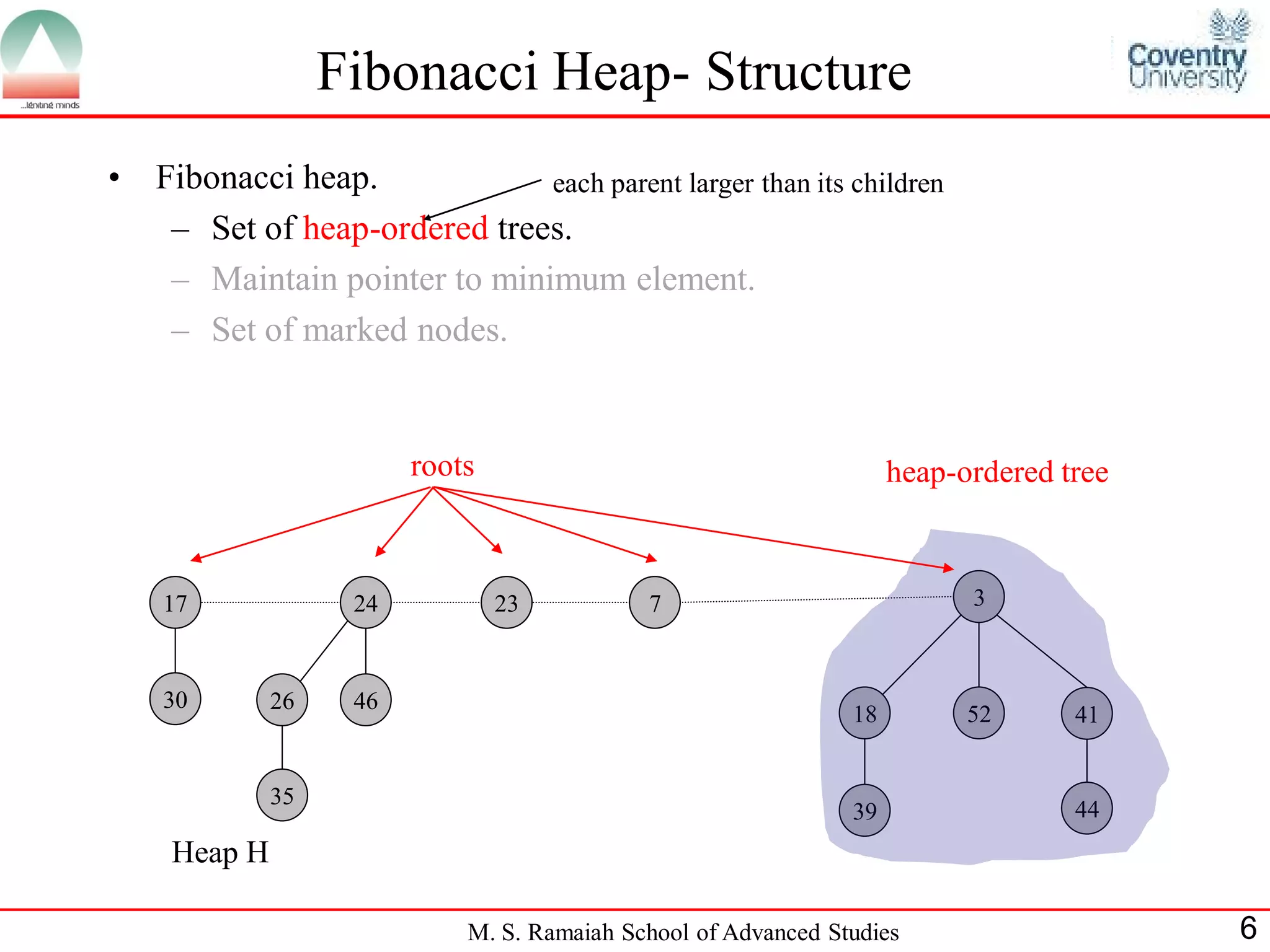
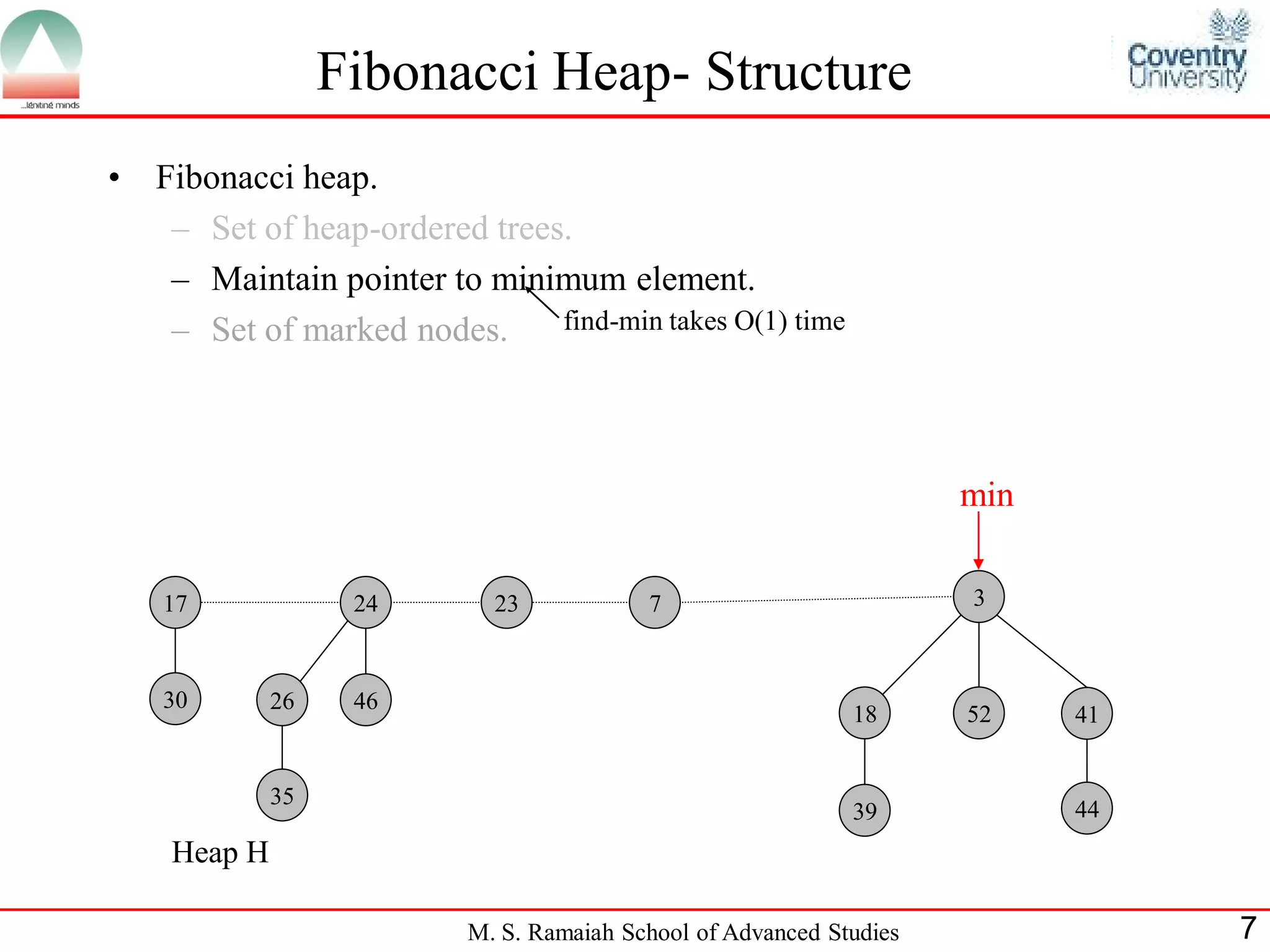
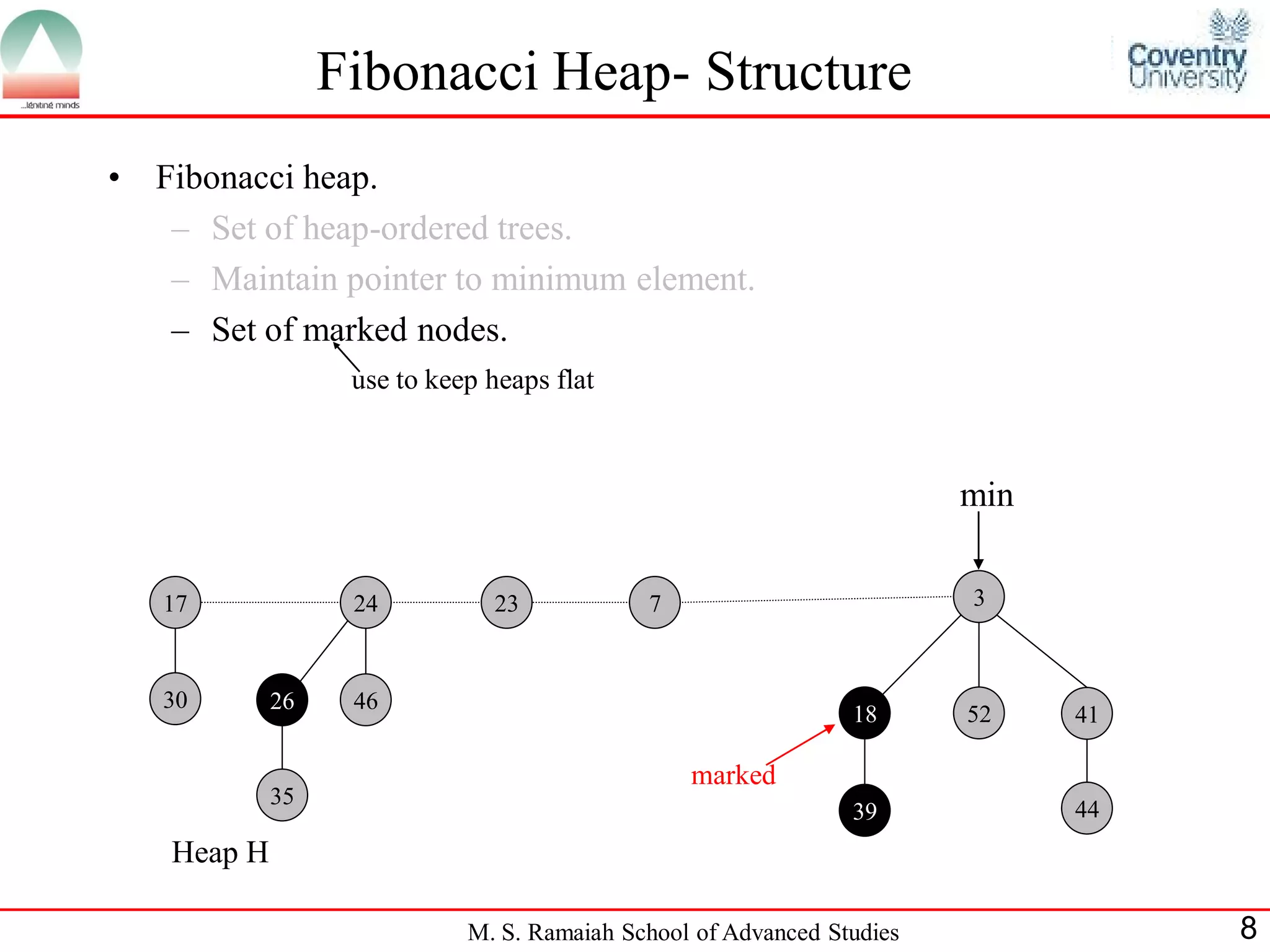
The document describes Fibonacci heaps, a data structure used to implement priority queues. A Fibonacci heap is a collection of trees with heap-ordered structure. It supports operations like insert, find minimum, extract minimum, decrease key, and delete in amortized O(1) time by lazily consolidating trees. The extract minimum operation does consolidation work to ensure no two roots have the same degree. Fibonacci heaps improve the running time of Dijkstra's shortest path algorithm compared to binomial heaps.

1. CSN2501 DSA Presentation
Fibonacci Heap
Anshuman Biswal
PT 2012 Batch, Reg. No.: CJB0412001
M. Sc. (Engg.) in Computer Science and Networking
Module Leader: N. D. Gangadhar
Module Name: Data Structures and Algorithms
Module Code : CSN2501
M. S. Ramaiah School of Advanced Studies 1

2. Marking
Head Maximum Score
Technical Content 10
Grasp and Understanding 10
Delivery – Technical and 10
General Aspects
Handling Questions 10
Total 40
M. S. Ramaiah School of Advanced Studies 2

3. Presentation Outline
• Introduction
• Fibonacci Heap Structure
• Fibonacci Heap Implementation
• Notations and Potential Function
• Fibonacci Heap Operations
– Make a Fibonacci heap
– Insert a node
– Find minimum
– Bounding the maximum degree and Linking operation
– Extract min
– Union
– Decrease key
– Delete key
• Analysis
• Fibonacci Heap Bounding the Rank
• Conclusion
• References
M. S. Ramaiah School of Advanced Studies 3

4. Introduction
• Fibonacci heap is a heap data structure consisting of collection of trees.
• It has a better amortized running time of binomial heap.
• Developed by Michael L Fredman and Robert E Tarjan in 1984 and
first published in the scientific journal in 1987.
• The name Fibonacci heap comes from the Fibonacci numbers which
are used in running time analysis.
• Fibo heaps are mostly used when the number of EXTRACT-
MIN and DELETE operations is small relative to the number of other
operations performed.
• Fibonacci heaps are loosely based on Binomial Heaps but have less
rigid structure.
• Fibonacci heaps are not good to use for operation Search.
• Original motivation: improve Dijkstra's shortest path algorithm
from O(E log V ) to O(E + V log V ). V insert, V delete-min, E decrease-key
M. S. Ramaiah School of Advanced Studies 4

5. Introduction
• Binomial heap: eagerly consolidate trees after each insert.
• Fibonacci heap: lazily defer consolidation until next delete-min.
• It also used for faster method for computing minimum spanning trees
with improvements from O(m log log base (m/n+2) of n) to
O(mβ)(m, n), where β(m, n) = min{i | log to the power i of n <= m/n}.
M. S. Ramaiah School of Advanced Studies 5

6. Fibonacci Heap- Structure
• Fibonacci heap. each parent larger than its children
– Set of heap-ordered trees.
– Maintain pointer to minimum element.
– Set of marked nodes.
roots heap-ordered tree
17 24 23 7 3
30 26 46
18 52 41
35
39 44
Heap H
M. S. Ramaiah School of Advanced Studies 6

7. Fibonacci Heap- Structure
• Fibonacci heap.
– Set of heap-ordered trees.
– Maintain pointer to minimum element.
– Set of marked nodes. find-min takes O(1) time
min
17 24 23 7 3
30 26 46
18 52 41
35
39 44
Heap H
M. S. Ramaiah School of Advanced Studies 7

8. Fibonacci Heap- Structure
• Fibonacci heap.
– Set of heap-ordered trees.
– Maintain pointer to minimum element.
– Set of marked nodes.
use to keep heaps flat
min
17 24 23 7 3
30 26 46
18 52 41
marked
35
39 44
Heap H
M. S. Ramaiah School of Advanced Studies 8

9. Fibonacci Heap- Implementation
– Represent trees using left-child, right sibling pointers and circular, doubly
linked list.
• Given two such lists ,we can quickly splice off sub trees or concatenate
in O(1) time
• Can remove or insert a node in O(1) time
– Roots of trees connected with circular doubly linked list.
• fast union
– Pointer to root of tree with min element.
min
• fast find-min
17 24 23 7 3
30 26 46
18 52 41
Heap H 35
39 44
M. S. Ramaiah School of Advanced Studies 9

10. Fibonacci Heap- Implementation
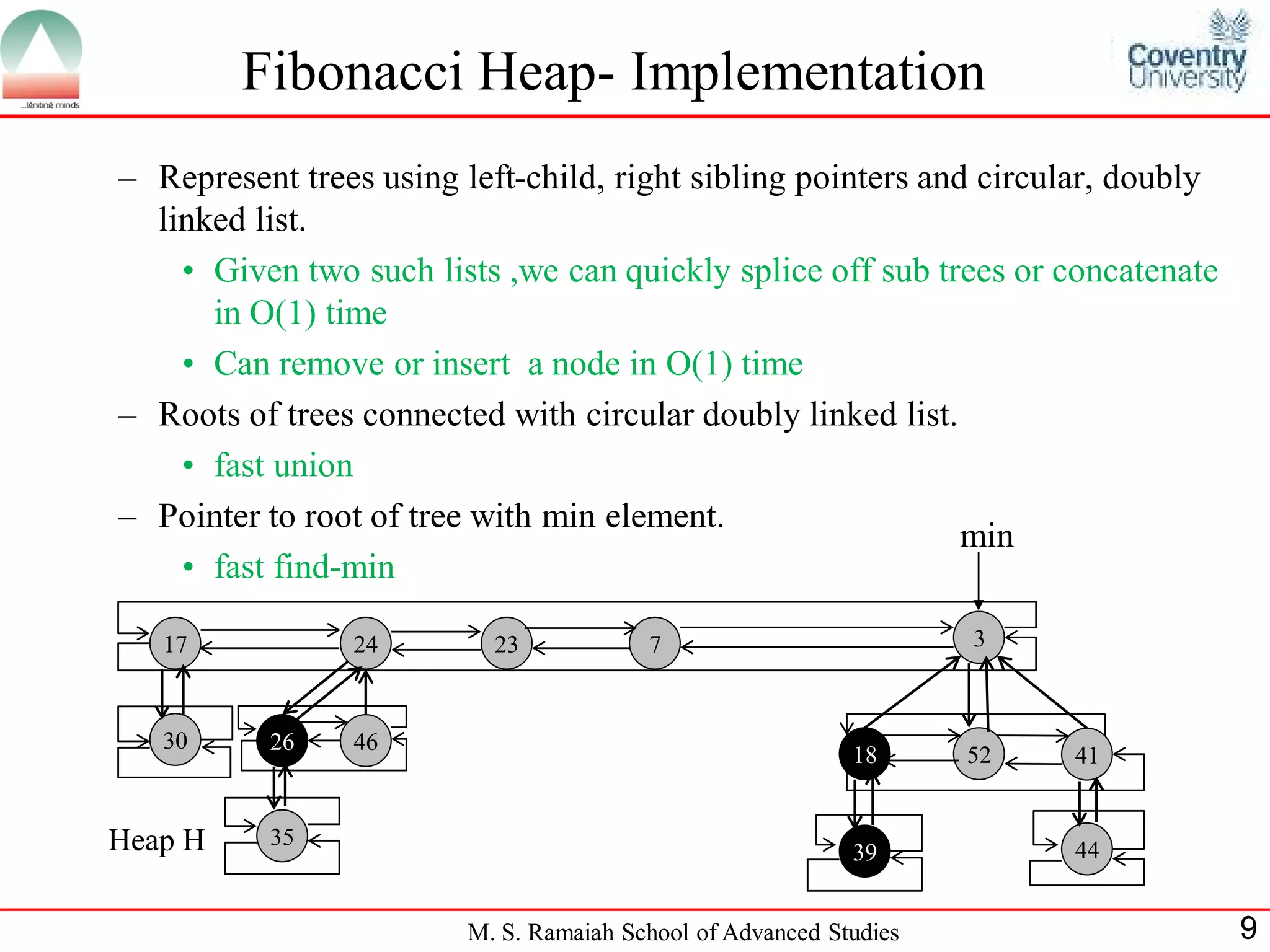
• Each node x has pointer p[x] to its parent & child [x] to one of its children
• Children are linked together in a doubly-linked circular list which is called the
child list of x.
• Each child y in a child list has pointers left[y] and right [y] which points to left
and right siblings.
• Left[y]==right[y]==y, then y is the only child
• Each node also has degree [x] indicating the number of children of x
min
17 24 23 7 3
30 26 46
18 52 41
Heap H 35
39 44
M. S. Ramaiah School of Advanced Studies 10

11. Fibonacci Heap- Implementation
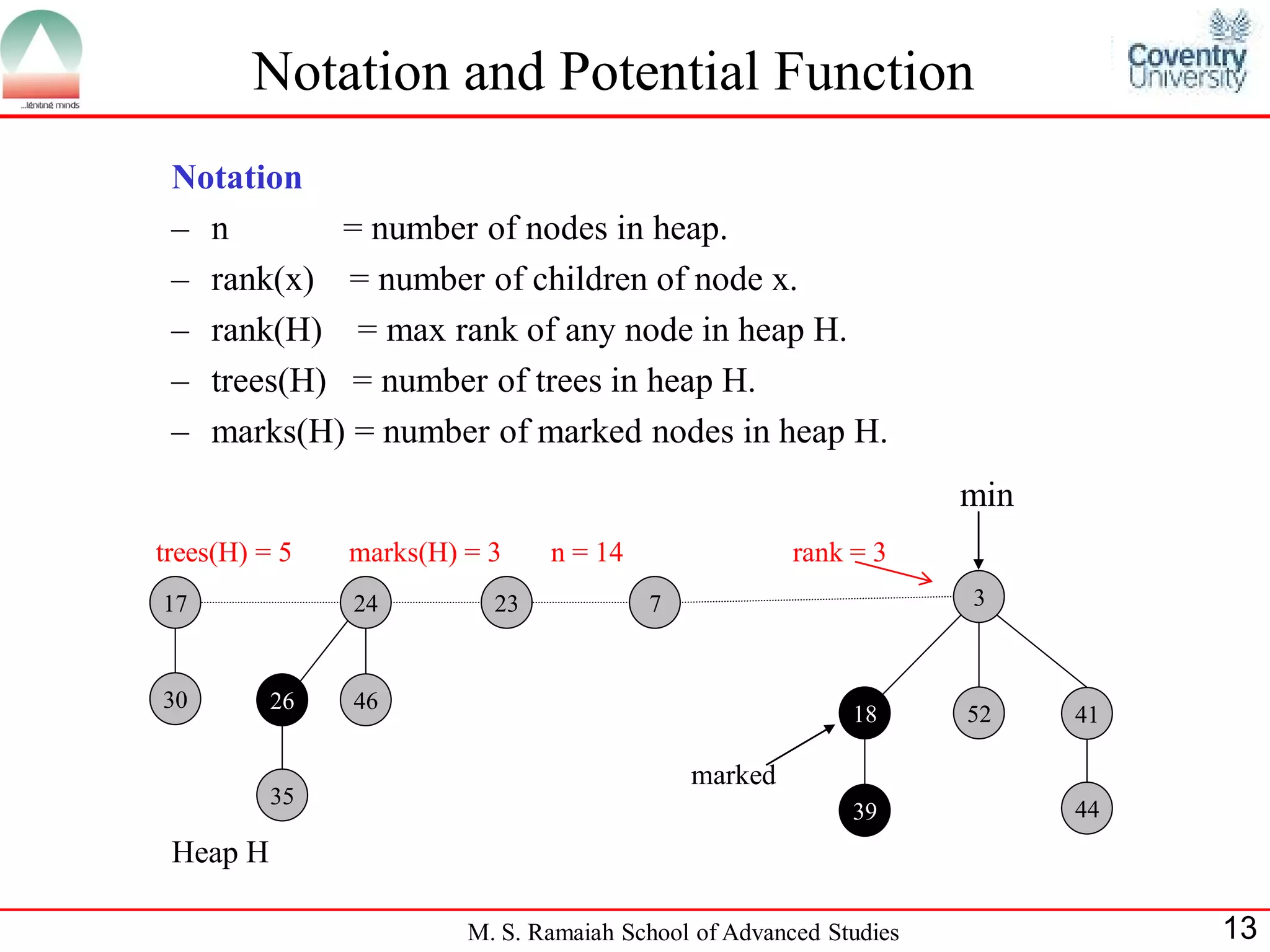
• Each node also has mark [x], a Boolean field indicating whether x has lost a
child since the last time x was made the child of another node
• Some nodes will be marked
(indicated by the marked bit set to 1).
(i) A node x will be marked if x has lost a child since the last time that x was
made a child of another node.
(ii) Newly created nodes are unmarked
(iii) When node x becomes child of another node it becomes unmarked
3 min = 3
17 24 23 7
30 26 46
18 52 41
Heap H 35
39 44
M. S. Ramaiah School of Advanced Studies 11

12. Fibonacci Heap- Implementation
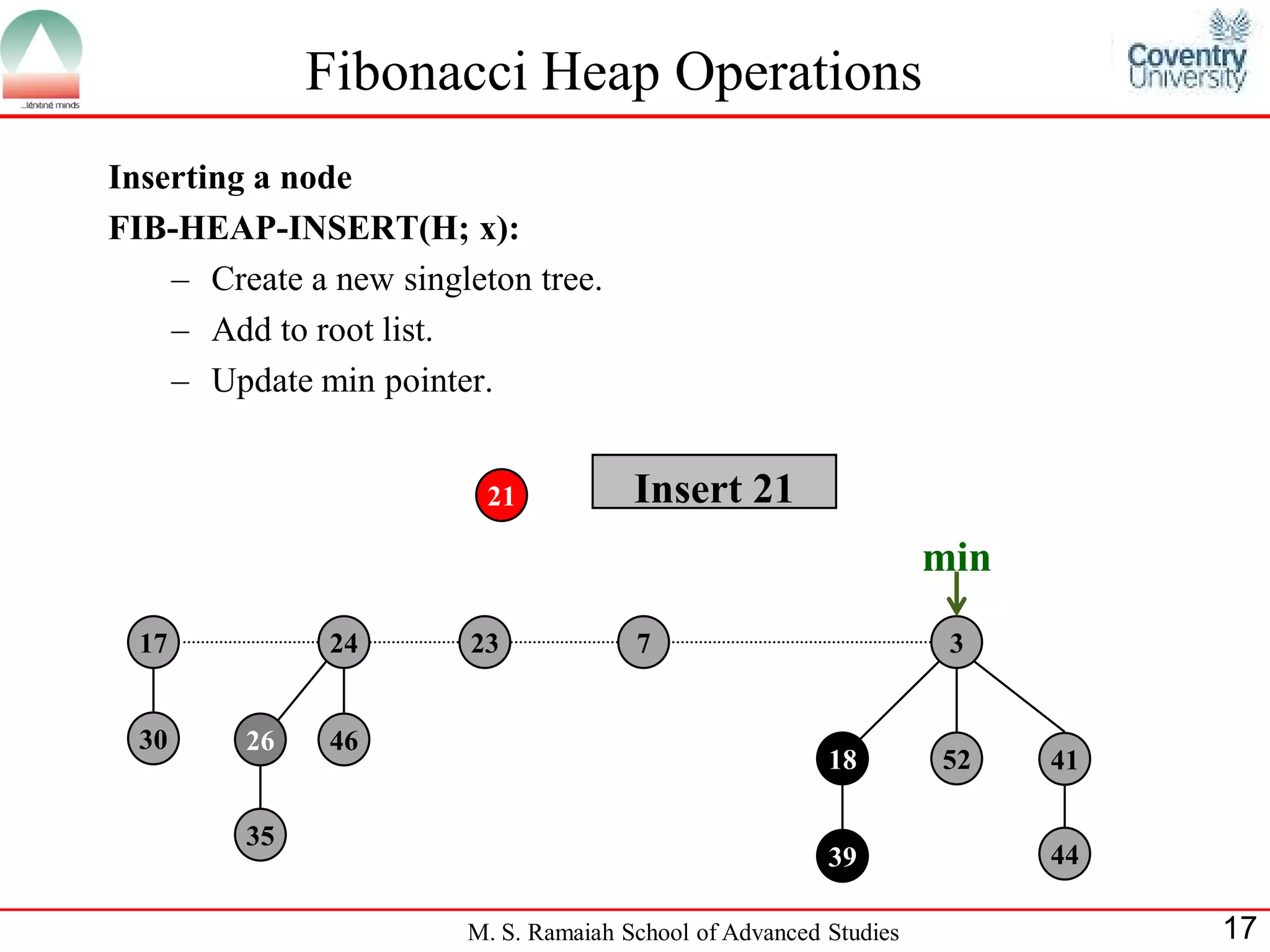
•The entire heap is accessed by a pointer min [H] which points to the minimum-
key root
•Min(H) = NIL => H is empty
min
17 24 23 7 3
30 26 46
18 52 41
Heap H 35
39 44
M. S. Ramaiah School of Advanced Studies 12

13. Notation and Potential Function
Notation
– n = number of nodes in heap.
– rank(x) = number of children of node x.
– rank(H) = max rank of any node in heap H.
– trees(H) = number of trees in heap H.
– marks(H) = number of marked nodes in heap H.
min
trees(H) = 5 marks(H) = 3 n = 14 rank = 3
17 24 23 7 3
30 26 46
18 52 41
marked
35
39 44
Heap H
M. S. Ramaiah School of Advanced Studies 13

14. Notation and Potential Function
Potential Function
(H) = trees(H) + 2  marks(H)
potential of heap H
trees(H) = 5 marks(H)=3 Ф (H) = 5 + 2.3 = 11
min
17 24 23 7 3
30 26 46
18 52 41
marked
35
39 44
Heap H
M. S. Ramaiah School of Advanced Studies 14

15. Fibonacci Heap Operations
• MAKE-FIB-HEAP(): creates and returns a new empty heap.
• FIB-HEAP-INSERT(H; x): inserts node x, whose key field has
already been filled in, into heap H.
• FIB-HEAP-MINIMUM(H): returns a pointer to the node with
minimum key in heap H.
• FIB-HEAP-EXTRACT-MIN(H): deletes the node from heap H
whose key is minimum, returning a pointer to the node.
• UNION(H1;H2): creates and returns a new heap that contains all
the nodes of heaps H1 and H2. Heaps H1 and H2 are “destroyed” by
this operation.
• FIB-HEAP-DECREASE-KEY(H; x; k) :assigns to node x within
heap H the new key value k. It is assumed that key ≤ x:key.
• FIB-HEAP-DELETE(H; x) :deletes node x from heap H.
M. S. Ramaiah School of Advanced Studies 15

16. Fibonacci Heap Operations
Creating a Heap
MAKE-FIB-HEAP():
• allocates and returns the Fibonacci heap object H with H.n = 0 and
H.min = NIL:
• There are no trees in H. (H) = 0
• Because t(H) = 0 and m(H) = 0, the potential of the empty Fibonacci
heap  (H) = 0
• For MAKE-FIB-HEAP: amortized cost = actual cost = O(1).
M. S. Ramaiah School of Advanced Studies 16

17. Fibonacci Heap Operations
Inserting a node
FIB-HEAP-INSERT(H; x):
– Create a new singleton tree.
– Add to root list.
– Update min pointer.
21 Insert 21
min
17 24 23 7 3
30 26 46
18 52 41
35
39 44
M. S. Ramaiah School of Advanced Studies 17

18. Fibonacci Heap Operations
FIB-HEAP-INSERT Analysis:
Let H = Input Fibonacci heap and H = Resulting Fibonacci heap.
Then t(H) = t(H) + 1 and m(H) = m(H)
 Increase in potential = ((t(H)+1 )+ 2m(H)) - (t(H) + 2m(H)) = 1
Since actual cost = O(1) ,so the amortized cost is O(1) + 1 = O(1)
min
17 24 23 7 21 3
30 26 46
18 52 41
35
39 44
M. S. Ramaiah School of Advanced Studies 18

19. Fibonacci Heap Operations
Finding the minimum node
FIB-HEAP-MINIMUM(H):
The minimum node of Fibonacci heap is given by the pointer H.min, so
we can find the minimum node in O(1) actual time.
Since the potential of H does not change, the amortized cost of the
operation is O(1)
M. S. Ramaiah School of Advanced Studies 19

20. Bounding the maximum degree
If all trees in the Fibonacci heap are unordered
binomial trees, then D(n) = log 2 n .But the
(cascading) cuts may cause the occurrence of trees
that are not unordered binomial. Therefore, a
slightly weaker result still holds: D(n) ≤ log  n
where  is the golden ratio and is defined as
(1+ 5) / 2 = 1.61803
M. S. Ramaiah School of Advanced Studies 20

21. Fibonacci Heap Operations
• Linking operation. Make larger root be a child of smaller root.
larger root smaller root still heap-ordered
15 3 3
56 24 18 52 41 15 18 52 41
77 39 44 56 24 39 44
tree T1 tree T2
77
tree T'
M. S. Ramaiah School of Advanced Studies 21

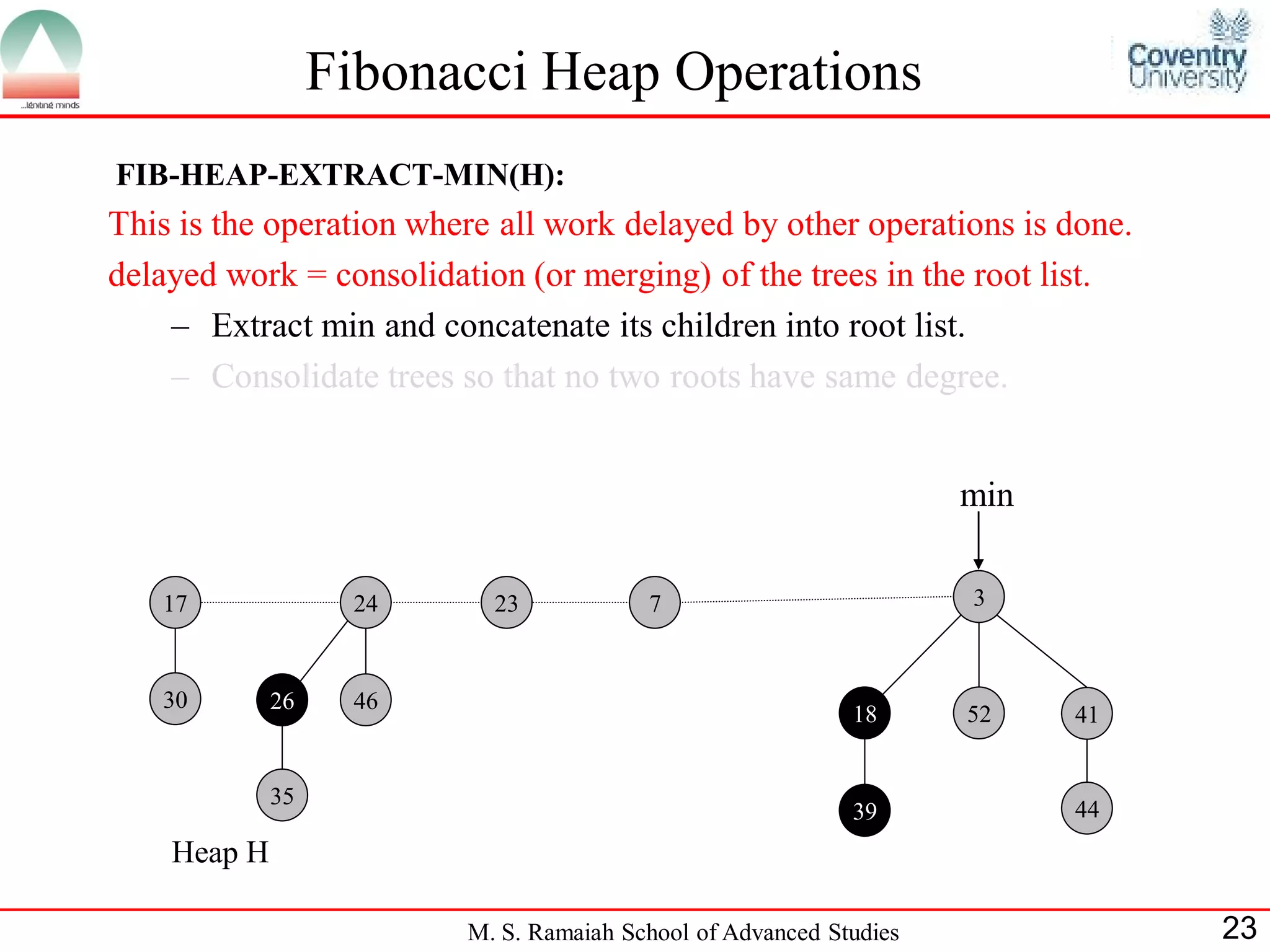
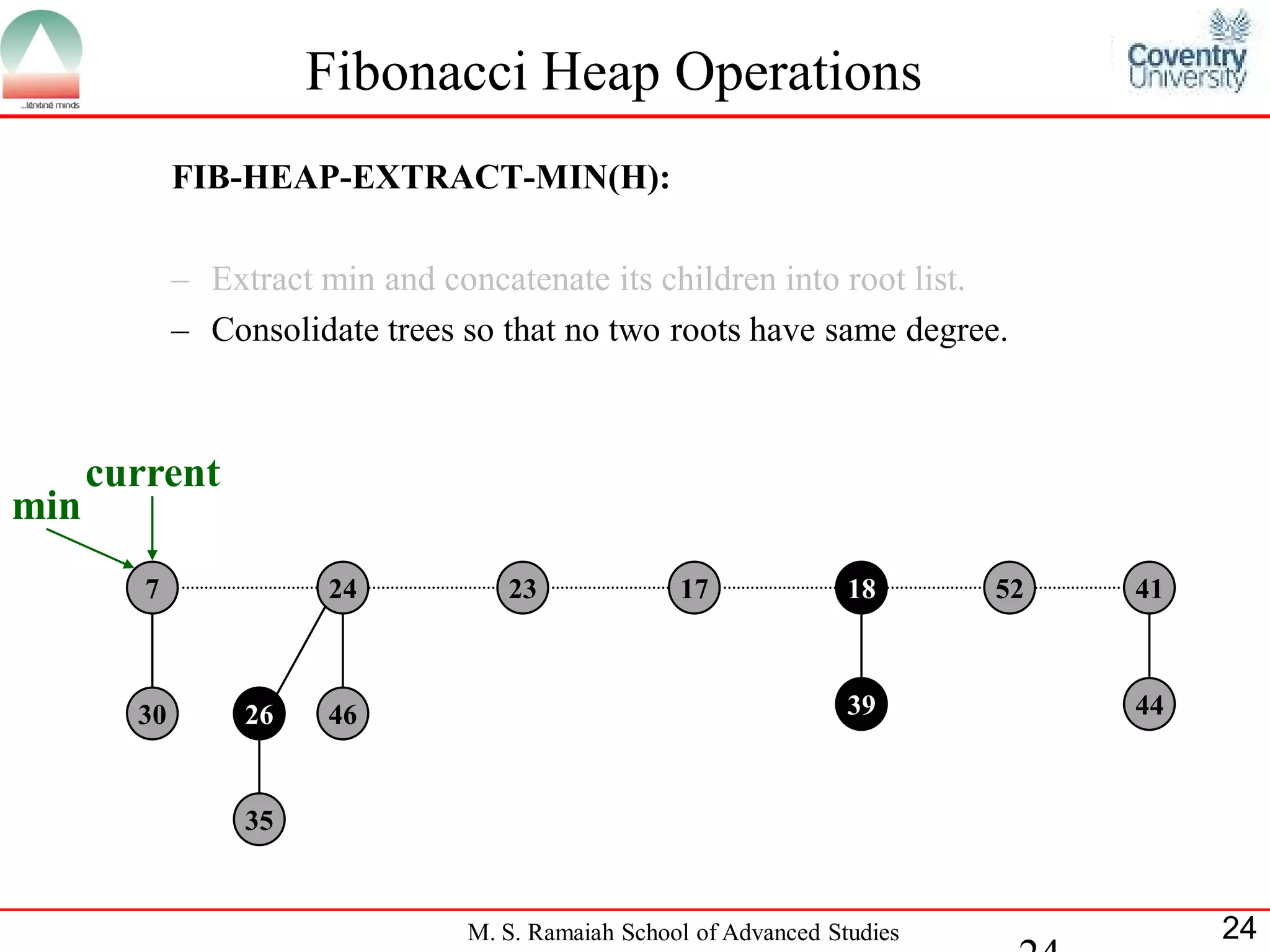
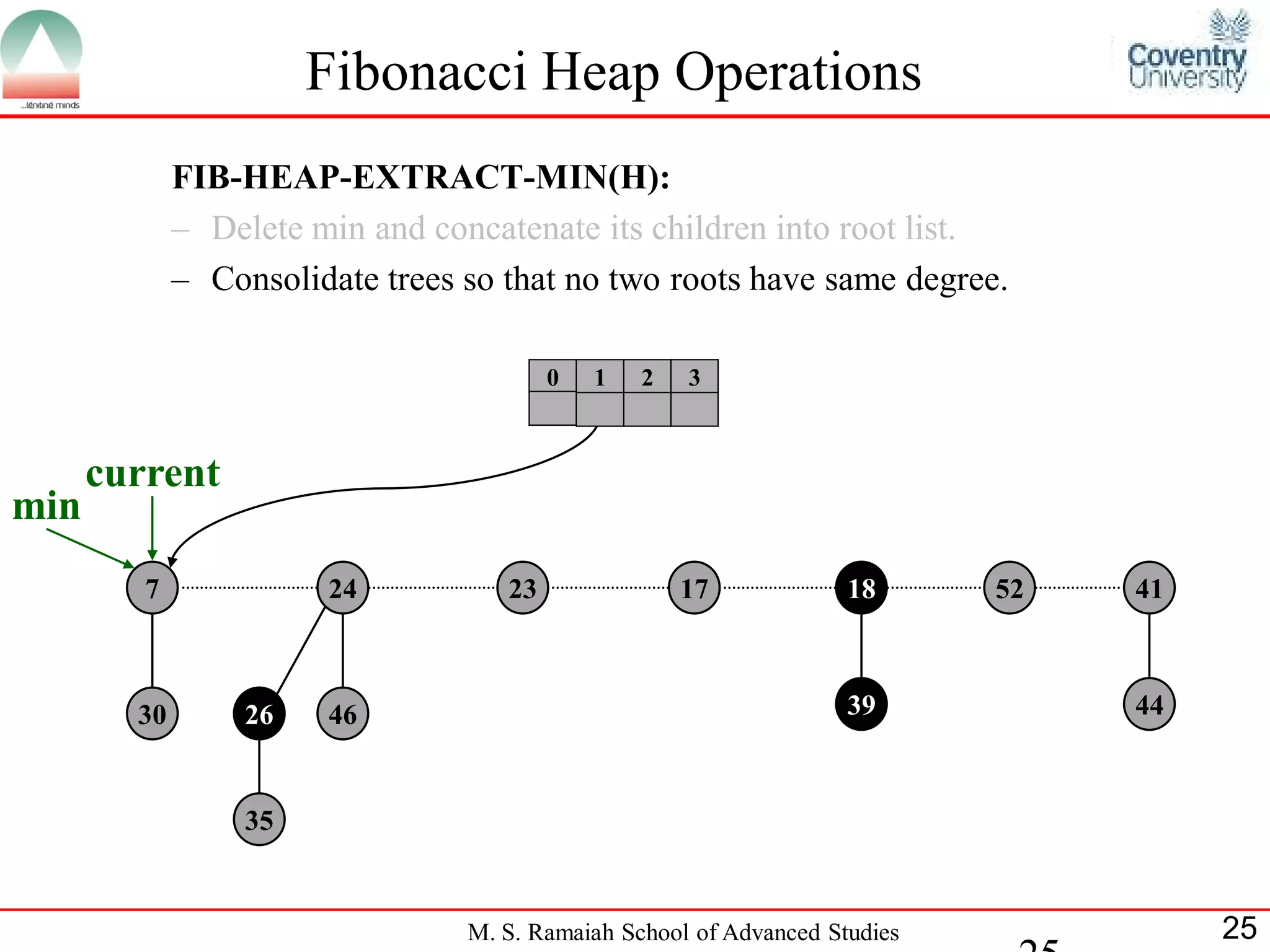
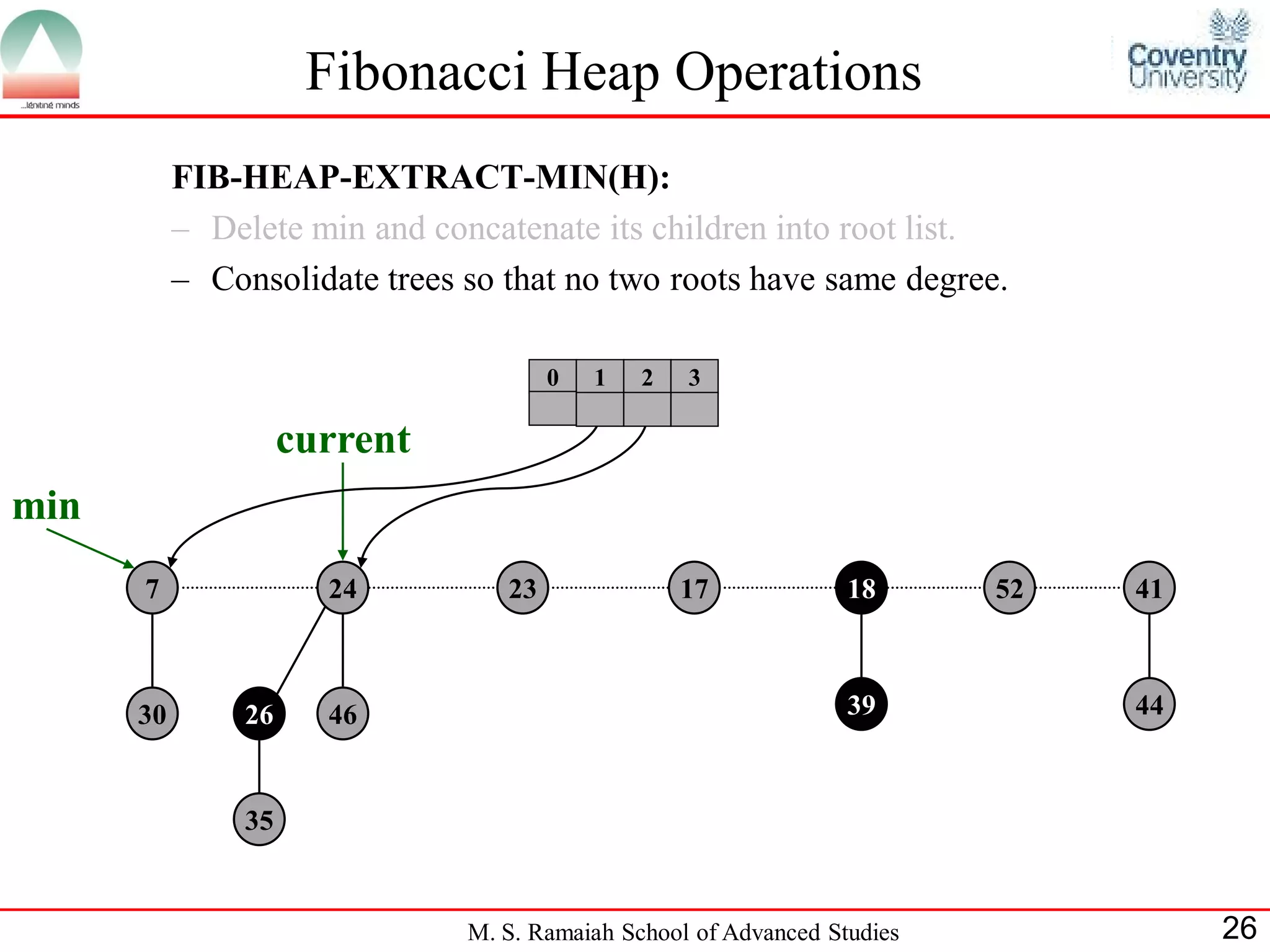
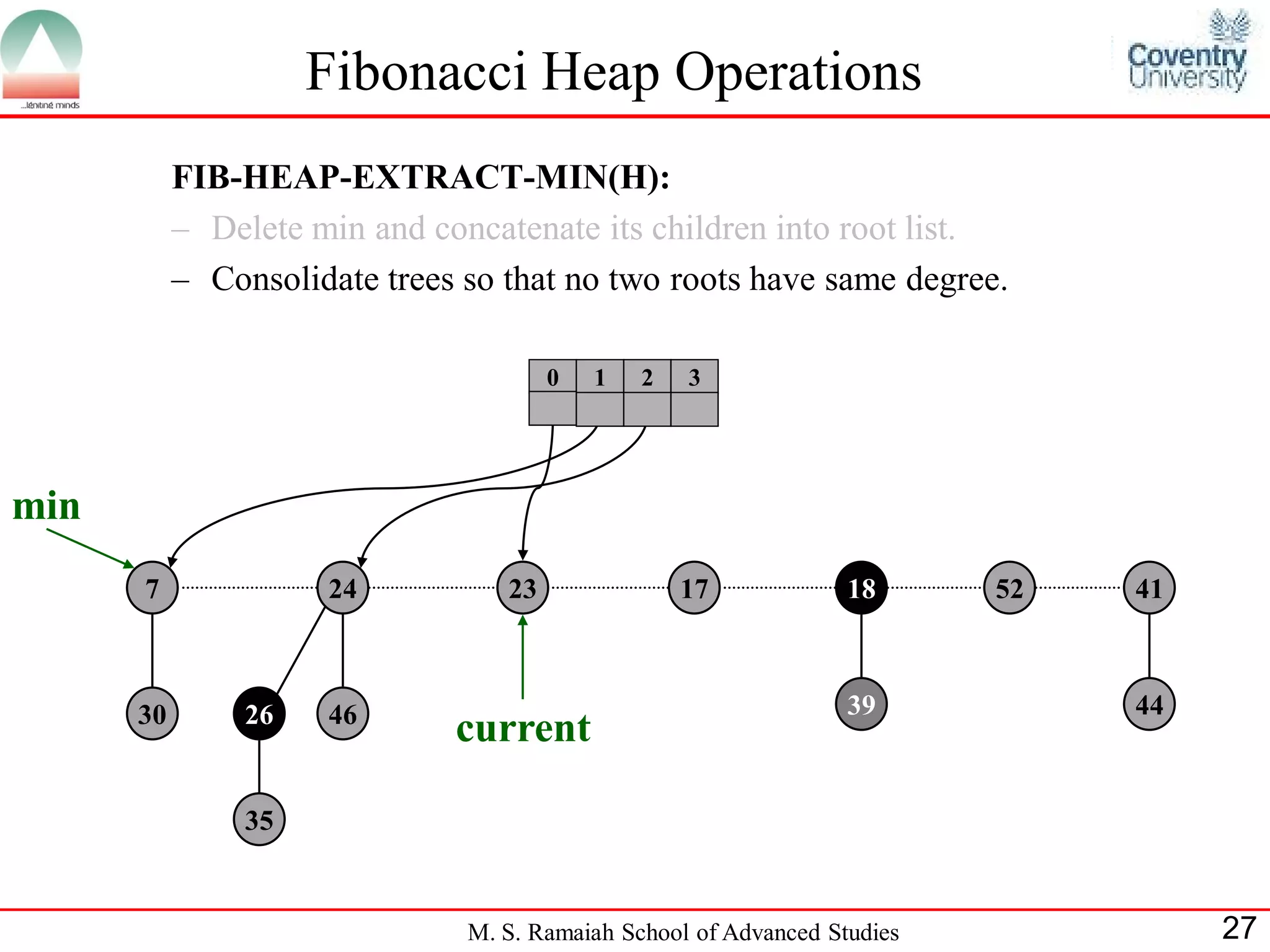
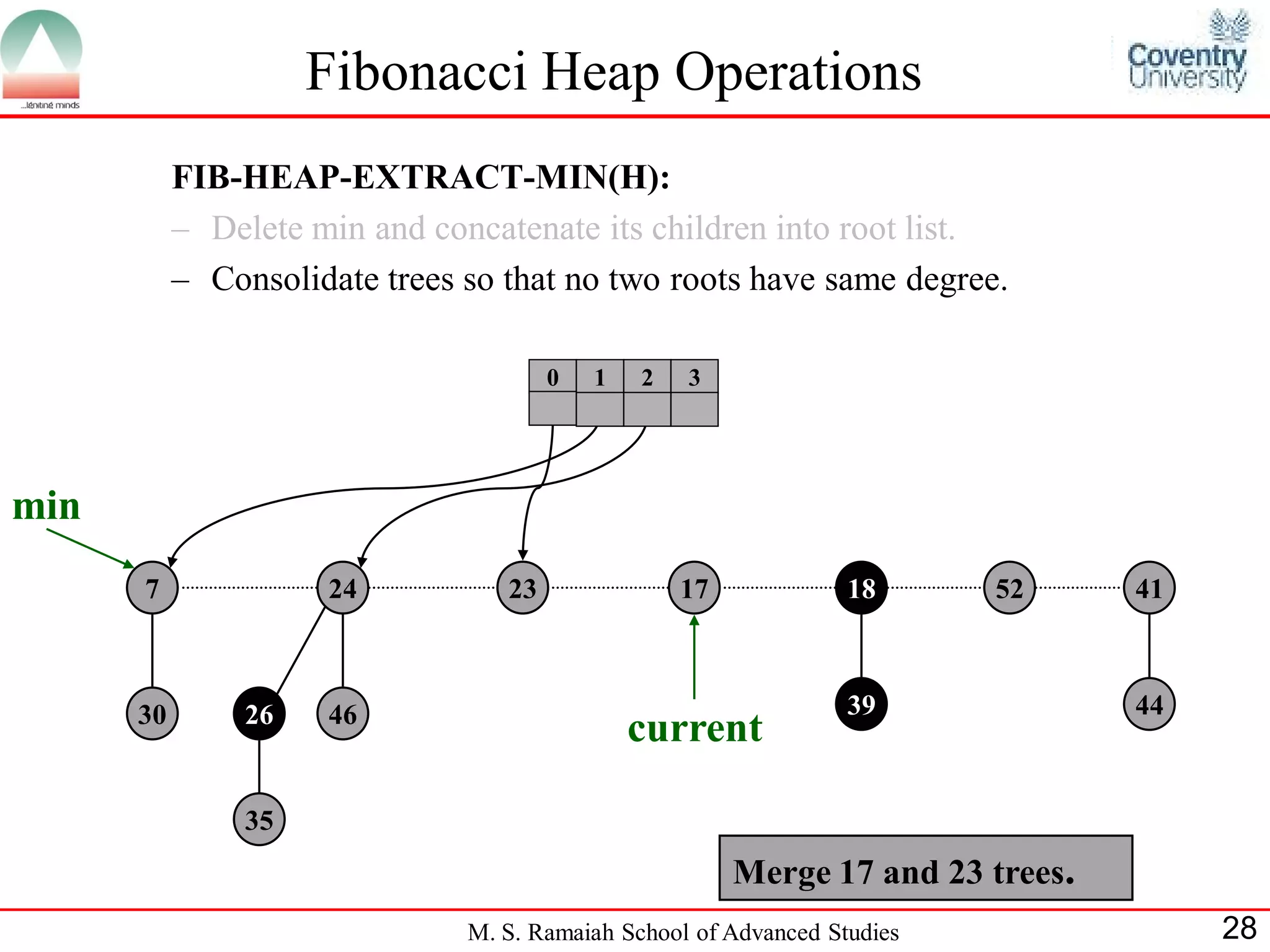
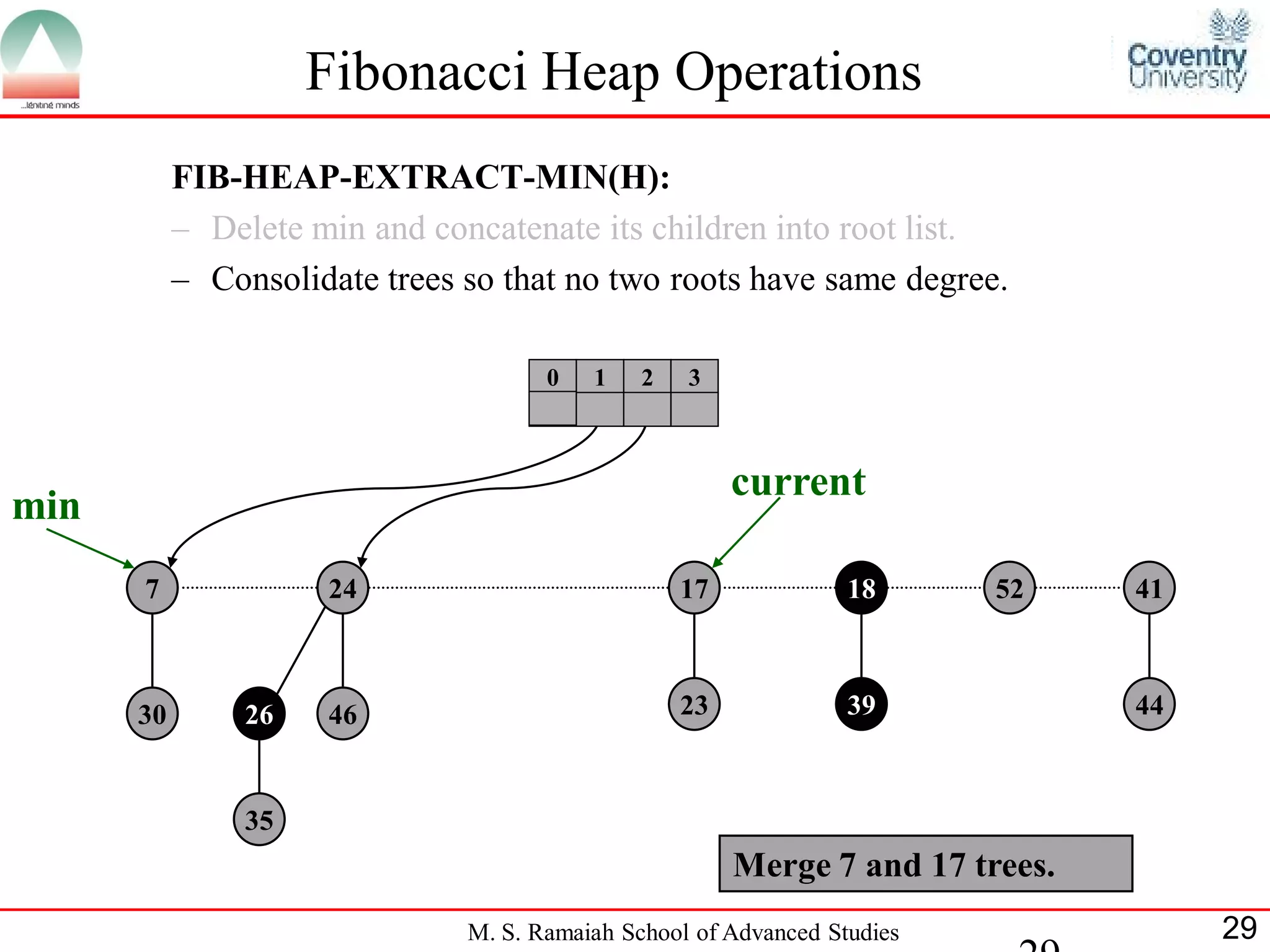
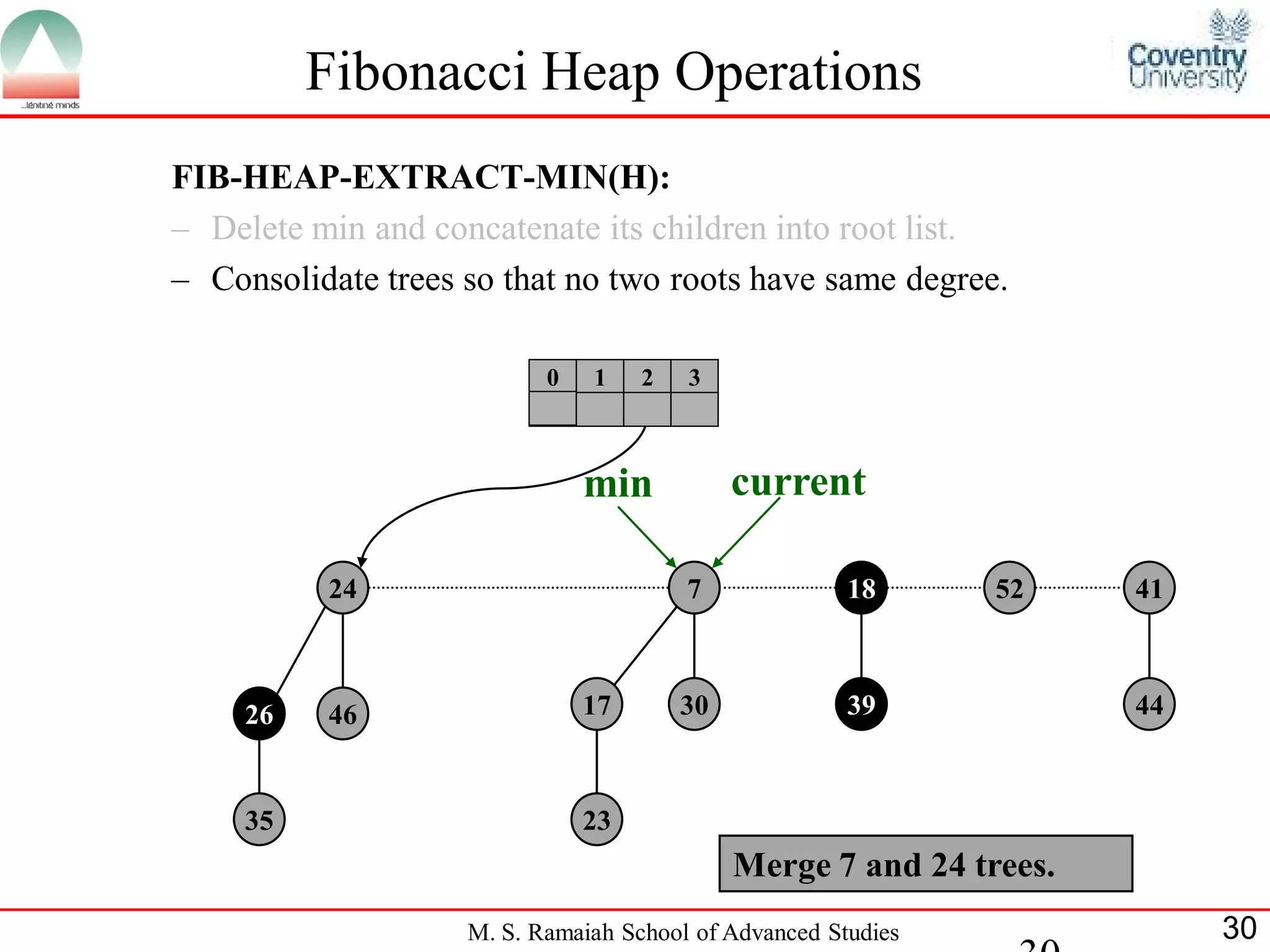
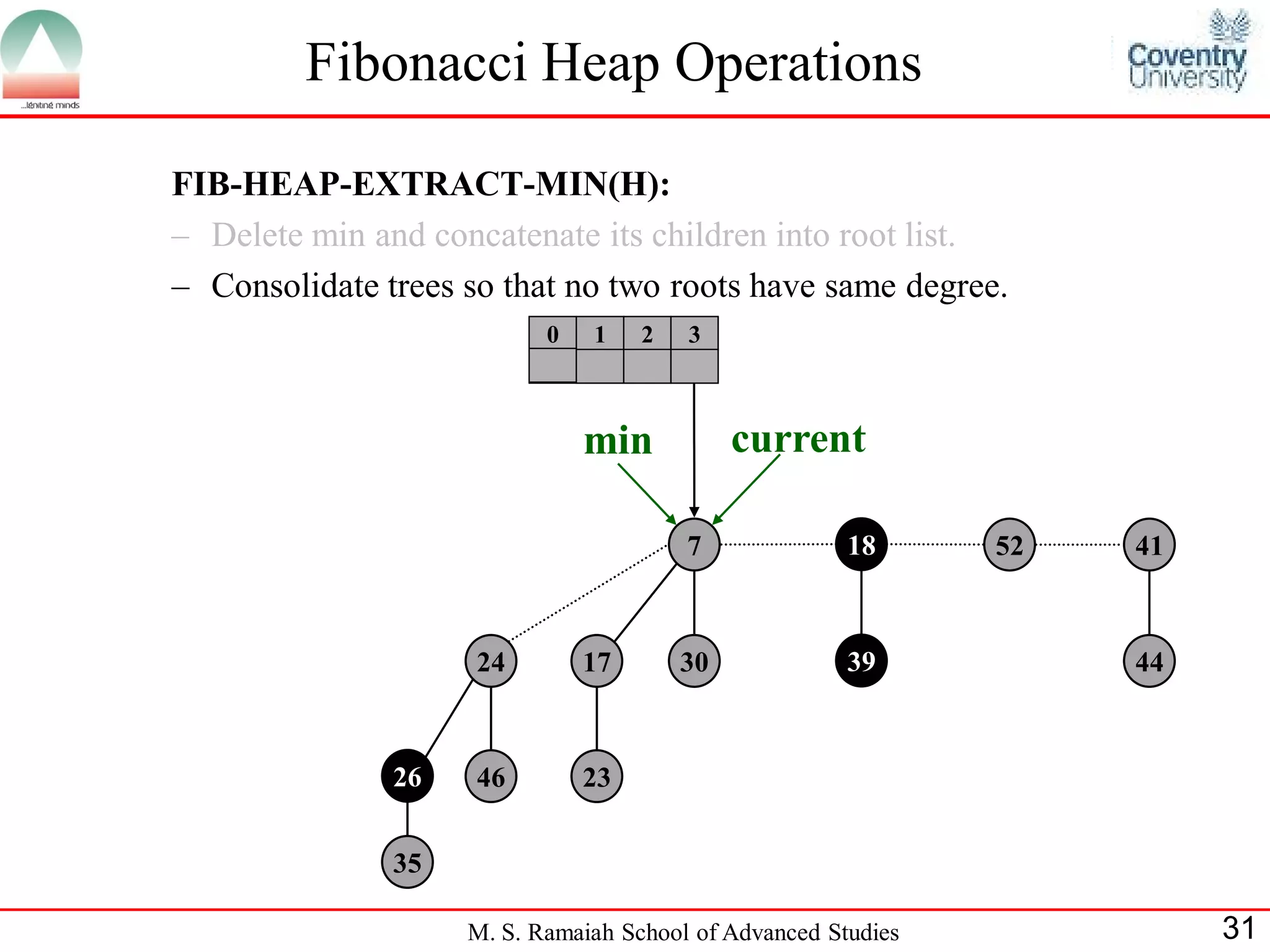
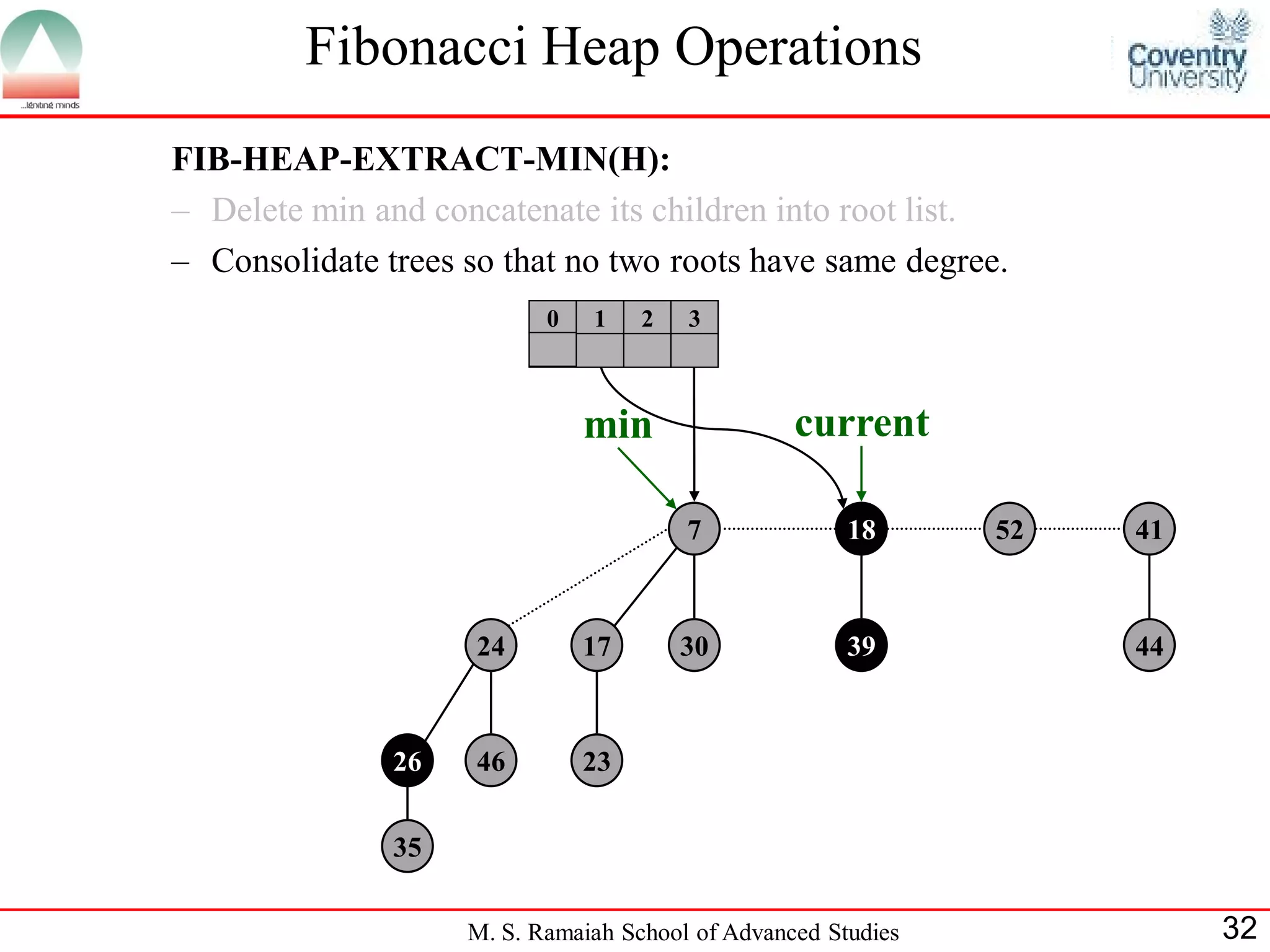
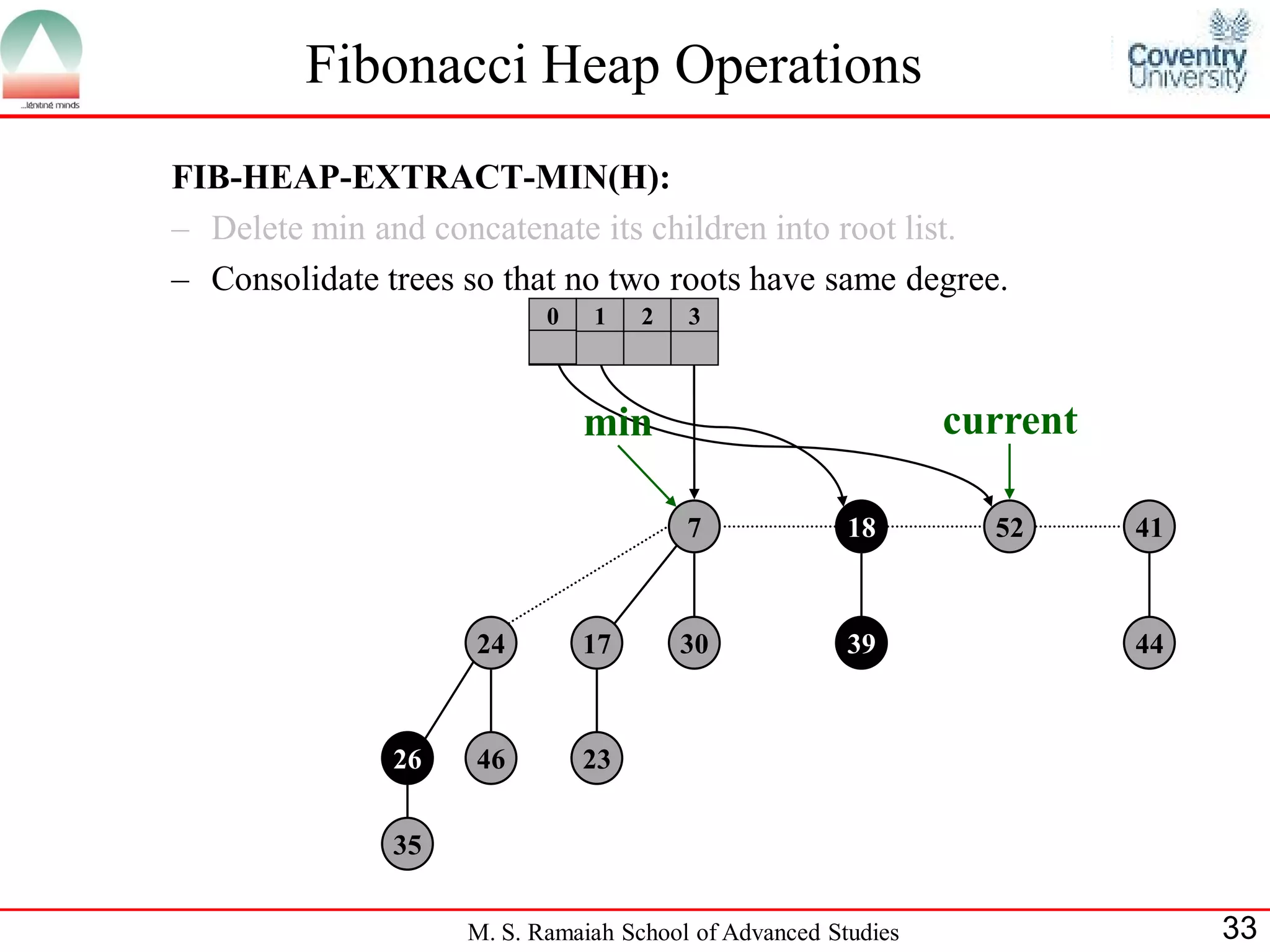
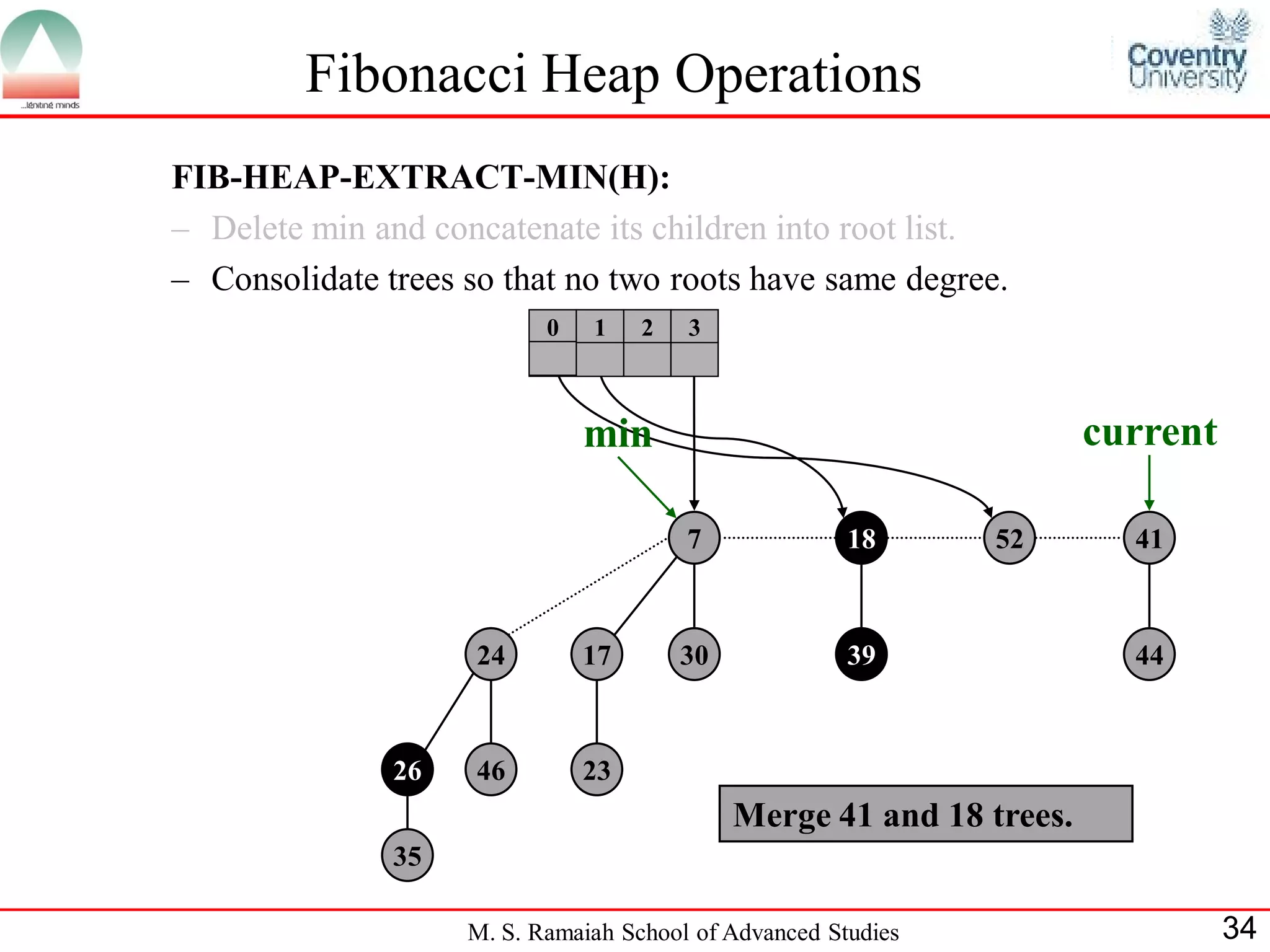
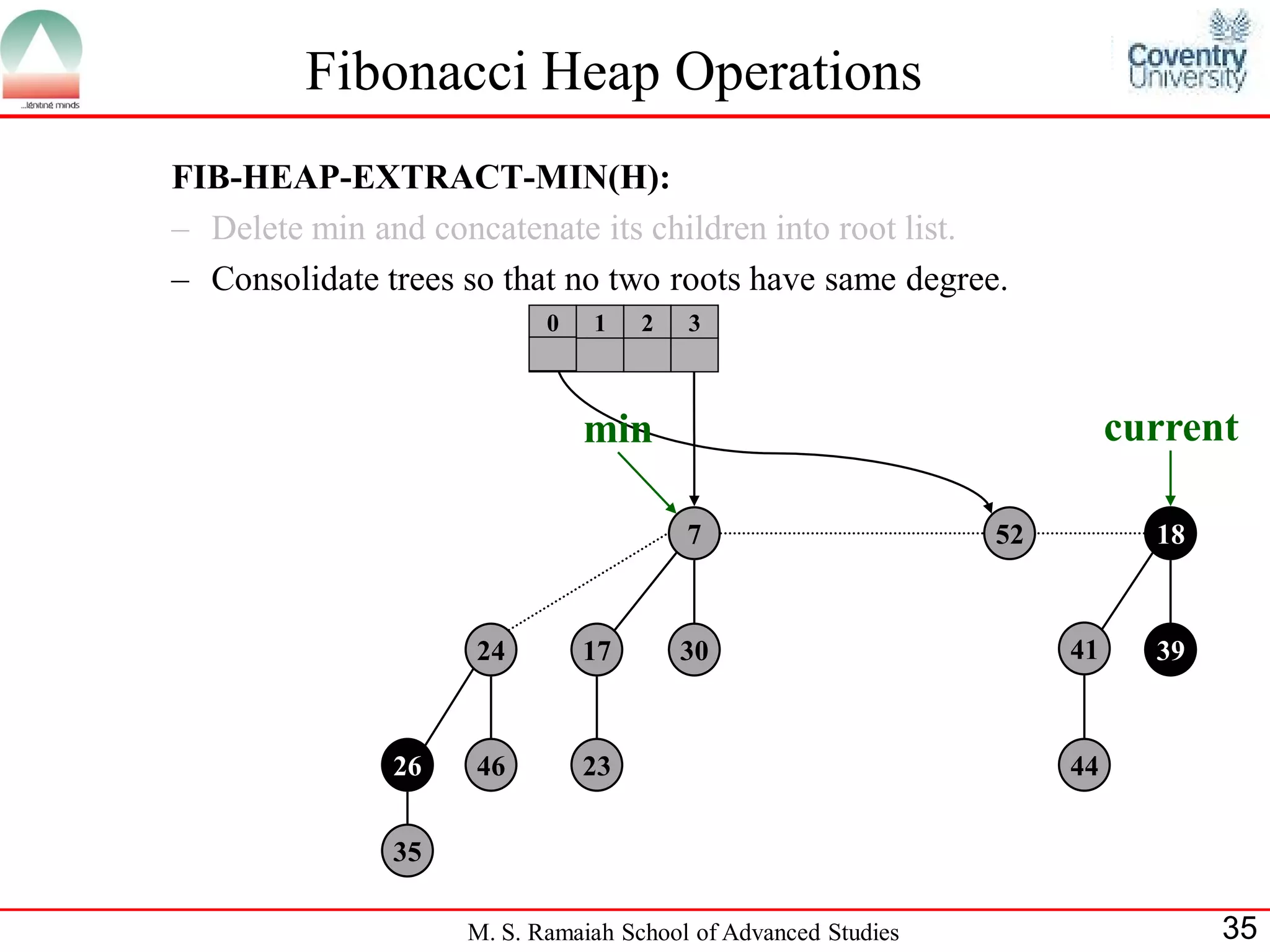
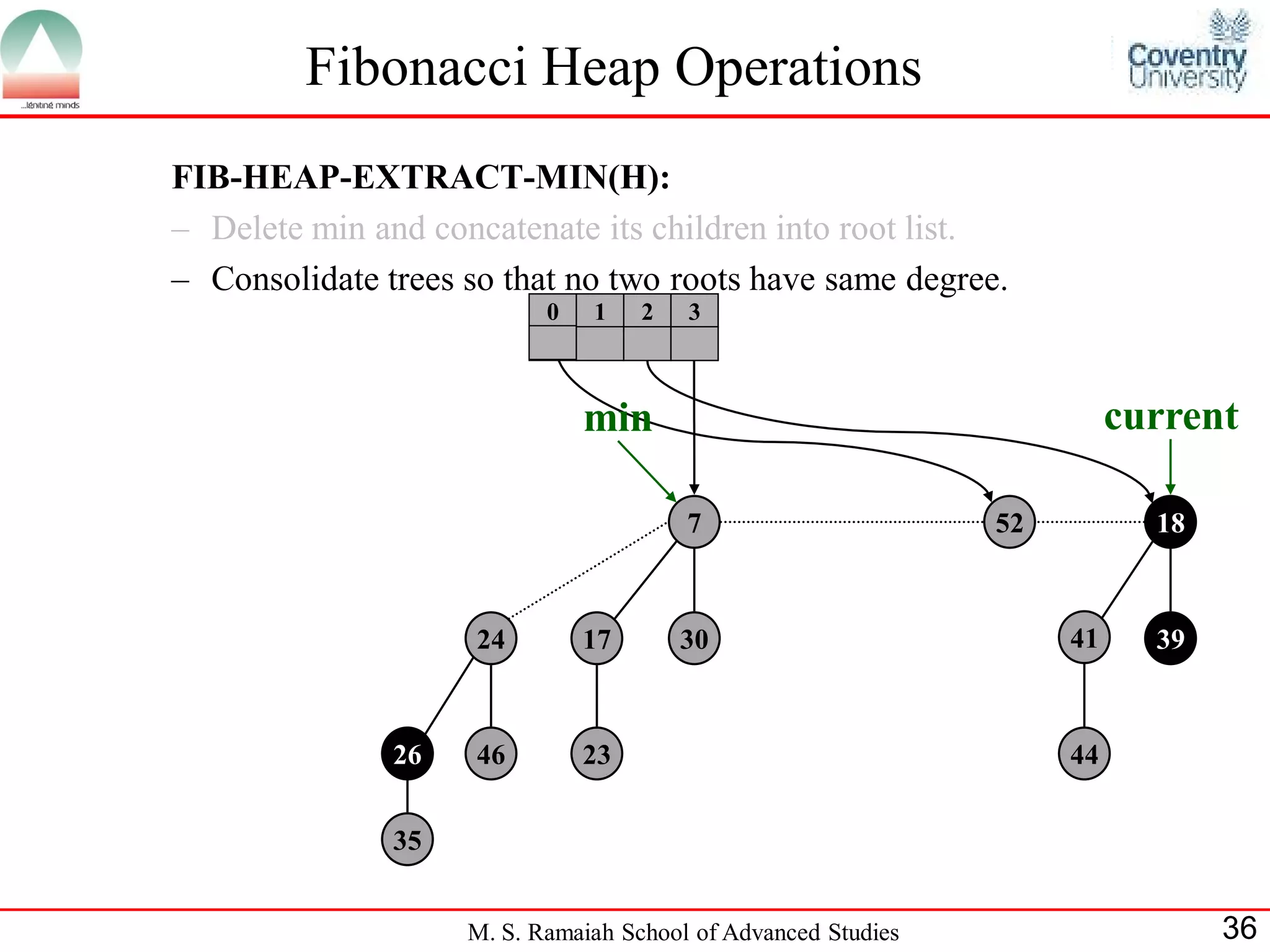
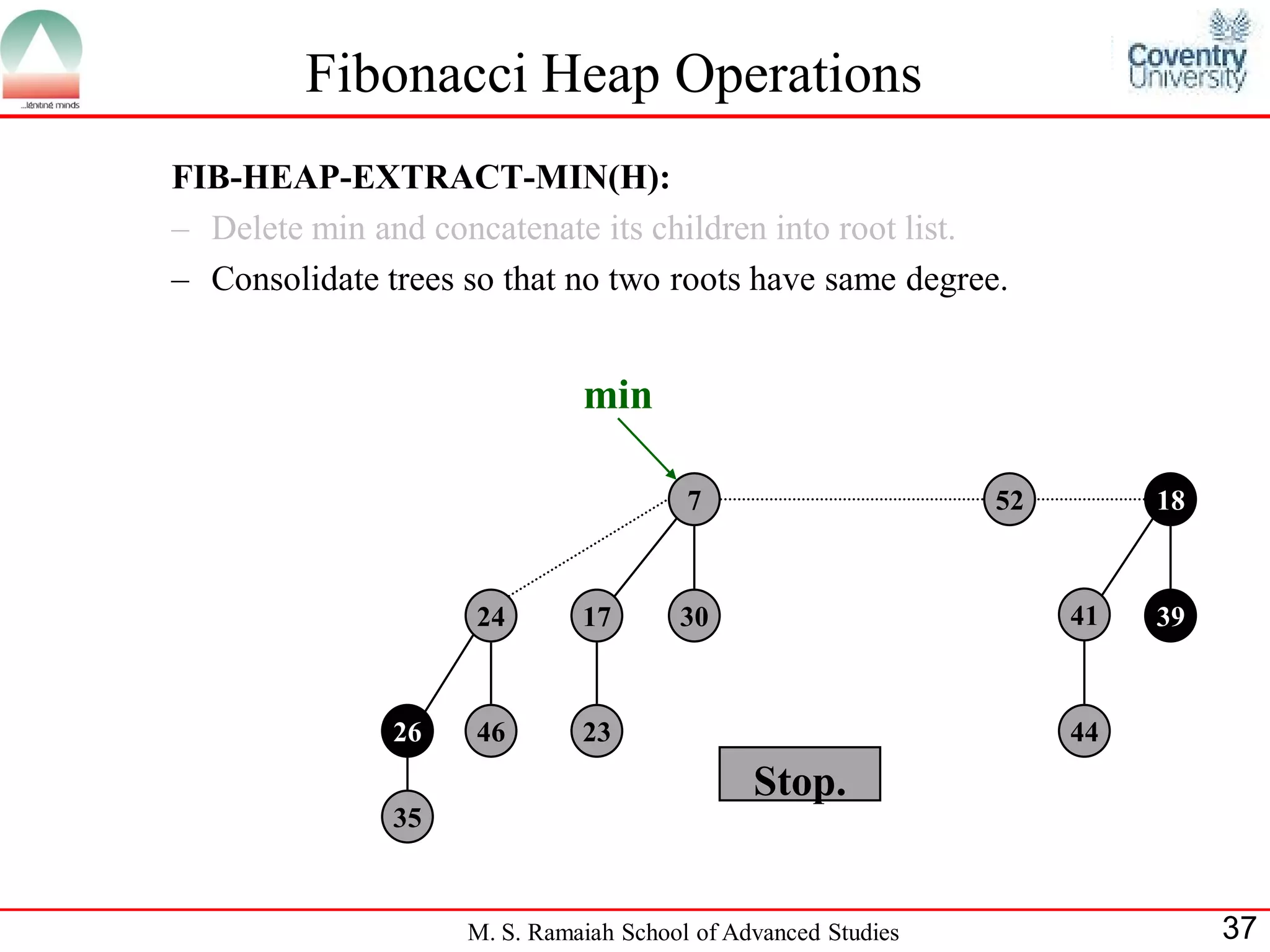
22. Fibonacci Heap Operations
• FIB-HEAP-EXTRACT-MIN makes a root out of each of the
minimum node-s children and removes the minimum node from the
root list.
• Next, it consolidates the root list by linking roots of equal degree until
at most one root remains of each degree.
• Consolidate(H) consolidates the root list of H by executing repeatedly
the following steps until every root in the root list has a distinct degree
value:
– Find two roots x and y from the root list with the same degree, and
with x->key y->key:
– Link y to x: remove y from the root list , and make y a child of x.
This operation is performed by FIB-HEAP-LINK.
• Consolidate(H) uses an auxiliary array A[0::D(H:n)]; if A[i] = y then
y is currently a root with y->degree = i:
M. S. Ramaiah School of Advanced Studies 22

23. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H):
This is the operation where all work delayed by other operations is done.
delayed work = consolidation (or merging) of the trees in the root list.
– Extract min and concatenate its children into root list.
– Consolidate trees so that no two roots have same degree.
min
17 24 23 7 3
30 26 46
18 52 41
35
39 44
Heap H
M. S. Ramaiah School of Advanced Studies 23

24. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H):
– Extract min and concatenate its children into root list.
– Consolidate trees so that no two roots have same degree.
current
min
7 24 23 17 18 52 41
30 26 46 39 44
35
M. S. Ramaiah School of Advanced Studies 24

25. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H):
– Delete min and concatenate its children into root list.
– Consolidate trees so that no two roots have same degree.
0 1 2 3
current
min
7 24 23 17 18 52 41
30 26 46 39 44
35
M. S. Ramaiah School of Advanced Studies 25

26. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H):
– Delete min and concatenate its children into root list.
– Consolidate trees so that no two roots have same degree.
0 1 2 3
current
min
7 24 23 17 18 52 41
30 26 46 39 44
35
M. S. Ramaiah School of Advanced Studies 26

27. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H):
– Delete min and concatenate its children into root list.
– Consolidate trees so that no two roots have same degree.
0 1 2 3
min
7 24 23 17 18 52 41
30 26 46 39 44
current
35
M. S. Ramaiah School of Advanced Studies 27

28. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H):
– Delete min and concatenate its children into root list.
– Consolidate trees so that no two roots have same degree.
0 1 2 3
min
7 24 23 17 18 52 41
30 26 46 39 44
current
35
Merge 17 and 23 trees.
M. S. Ramaiah School of Advanced Studies 28

29. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H):
– Delete min and concatenate its children into root list.
– Consolidate trees so that no two roots have same degree.
0 1 2 3
current
min
7 24 17 18 52 41
30 26 46 23 39 44
35
Merge 7 and 17 trees.
M. S. Ramaiah School of Advanced Studies 29

30. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H):
– Delete min and concatenate its children into root list.
– Consolidate trees so that no two roots have same degree.
0 1 2 3
min current
24 7 18 52 41
26 46 17 30 39 44
35 23
Merge 7 and 24 trees.
M. S. Ramaiah School of Advanced Studies 30

31. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H):
– Delete min and concatenate its children into root list.
– Consolidate trees so that no two roots have same degree.
0 1 2 3
min current
7 18 52 41
24 17 30 39 44
26 46 23
35
M. S. Ramaiah School of Advanced Studies 31

32. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H):
– Delete min and concatenate its children into root list.
– Consolidate trees so that no two roots have same degree.
0 1 2 3
min current
7 18 52 41
24 17 30 39 44
26 46 23
35
M. S. Ramaiah School of Advanced Studies 32

33. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H):
– Delete min and concatenate its children into root list.
– Consolidate trees so that no two roots have same degree.
0 1 2 3
min current
7 18 52 41
24 17 30 39 44
26 46 23
35
M. S. Ramaiah School of Advanced Studies 33

34. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H):
– Delete min and concatenate its children into root list.
– Consolidate trees so that no two roots have same degree.
0 1 2 3
min current
7 18 52 41
24 17 30 39 44
26 46 23
Merge 41 and 18 trees.
35
M. S. Ramaiah School of Advanced Studies 34

35. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H):
– Delete min and concatenate its children into root list.
– Consolidate trees so that no two roots have same degree.
0 1 2 3
min current
7 52 18
24 17 30 41 39
26 46 23 44
35
M. S. Ramaiah School of Advanced Studies 35

36. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H):
– Delete min and concatenate its children into root list.
– Consolidate trees so that no two roots have same degree.
0 1 2 3
min current
7 52 18
24 17 30 41 39
26 46 23 44
35
M. S. Ramaiah School of Advanced Studies 36

37. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H):
– Delete min and concatenate its children into root list.
– Consolidate trees so that no two roots have same degree.
min
7 52 18
24 17 30 41 39
26 46 23 44
Stop.
35
M. S. Ramaiah School of Advanced Studies 37

38. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H): Example 2 [1]
min
23 7 21 3 17 24
30 26 46
18 52 38
35
39 41
M. S. Ramaiah School of Advanced Studies 38

39. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H): Example 2 [1]
23 7 21 18 52 38 17 24
39 41 30 26 46
35
M. S. Ramaiah School of Advanced Studies 39

40. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H): Example 2 [1]
0 1 2 3
x
23 7 21 18 52 38 17 24
39 41 30 26 46
35
M. S. Ramaiah School of Advanced Studies 40

41. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H): Example 2 [1]
0 1 2 3
x
23 7 21 18 52 38 17 24
39 41 30 26 46
35
M. S. Ramaiah School of Advanced Studies 41

42. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H): Example 2 [1]
0 1 2 3
x
23 7 21 18 52 38 17 24
39 41 30 26 46
35
M. S. Ramaiah School of Advanced Studies 42

43. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H): Example 2 [1]
0 1 2 3
x
23 7 21 18 52 38 17 24
39 41 30 26 46
35
Merge 7,23
M. S. Ramaiah School of Advanced Studies 43

44. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H): Example 2 [1]
0 1 2 3
x
7 21 18 52 38 17 24
39 41 30 26 46
23
35
Merge 7,17
M. S. Ramaiah School of Advanced Studies 44

45. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H): Example 2 [1]
0 1 2 3
x
7 21 18 52 38 24
17
39 41 26 46
23
30 35
Merge 7,24
M. S. Ramaiah School of Advanced Studies 45

46. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H): Example 2 [1]
0 1 2 3
x
7 21 18 52 38
17
39 41
23 24
30
26 46
35
M. S. Ramaiah School of Advanced Studies 46

47. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H): Example 2 [1]
0 1 2 3
x
7 21 18 52 38
17
39 41
23 24
30
26 46
35
M. S. Ramaiah School of Advanced Studies 47

48. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H): Example 2 [1]
0 1 2 3
x
7 21 18 52 38
17
39 41
23 24
30
26 46
35
Merge 21,52
M. S. Ramaiah School of Advanced Studies 48

49. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H): Example 2 [1]
0 1 2 3
x
7 21 18 38
17
52 39 41
23 24
30
26 46
35
Merge 18,21
M. S. Ramaiah School of Advanced Studies 49

50. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H): Example 2 [1]
0 1 2 3
x
7 18 38
17 21
39 41
23 24
30 52
26 46
35
M. S. Ramaiah School of Advanced Studies 50

51. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN(H): Example 2 [1]
0 1 2 3
x
7 18 38
17 21
39 41
23 24
30 52
26 46
35
Stop
M. S. Ramaiah School of Advanced Studies 51

52. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN Analysis
• Notation.
– D(n) = max degree of any node in Fibonacci heap with n nodes.
– t(H) = # trees in heap H.
– (H) = t(H) + 2m(H).
• Actual cost. O(D(n) + t(H))
– O(D(n)) work adding min's children into root list and updating
min.
• at most D(n) children of min node
– O(D(n) + t(H)) work consolidating trees.
• work is proportional to size of root list since number of roots
decreases by one after each merging
•  D(n) + t(H) - 1 root nodes at beginning of consolidation
M. S. Ramaiah School of Advanced Studies 52

53. Fibonacci Heap Operations
FIB-HEAP-EXTRACT-MIN Analysis
• The potential before extracting the minimum node is t(H) + 2m(H).
• At most D(n) + 1 roots remain and no nodes become marked during
the operation => the potential after extracting the minimum node is
≤(D(n) + 1) + 2m(H).
=> the amortized cost is at most
P(D(n) + t(H)) + ((D(n) + 1) + 2m(H)) - (t(H) + 2m(H))
= O(D(n)) + O(t(H)) - t(H)
= O(D(n))
because the units of potential can be scaled to dominate the constant
hidden in O(t(H)):
M. S. Ramaiah School of Advanced Studies 53

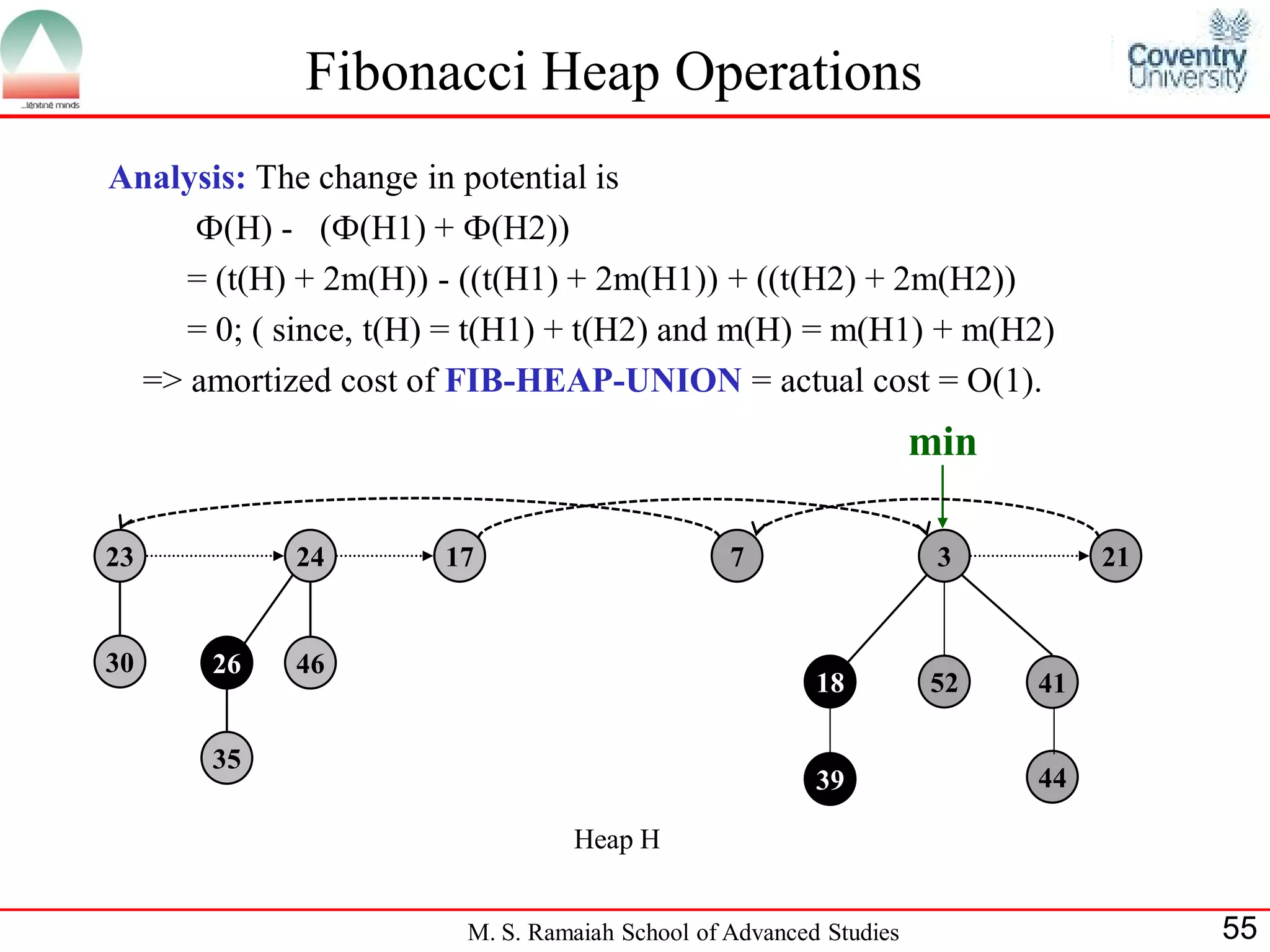
54. Fibonacci Heap Operations
FIB-HEAP-UNION(H1,H2)
1. Concatenate the root list of H1 and H2 into new root list H
2. Set the minimum node of H
3. Set n[H] to total number of nodes
min min
23 24 17 7 3 21
30 26 46
18 52 41
35
39 44
Heap H2
Heap H1
M. S. Ramaiah School of Advanced Studies 54

55. Fibonacci Heap Operations
Analysis: The change in potential is
Ф(H) - (Ф(H1) + Ф(H2))
= (t(H) + 2m(H)) - ((t(H1) + 2m(H1)) + ((t(H2) + 2m(H2))
= 0; ( since, t(H) = t(H1) + t(H2) and m(H) = m(H1) + m(H2)
=> amortized cost of FIB-HEAP-UNION = actual cost = O(1).
min
23 24 17 7 3 21
30 26 46
18 52 41
35
39 44
Heap H
M. S. Ramaiah School of Advanced Studies 55

56. Fibonacci Heap Operations
• FIB-HEAP-DECREASE-KEY(H; x; k)
– Case 1: min-heap property not violated.
• decrease key of x to k
• change heap min pointer if necessary
min
7 18 38
24 17 23 21 39 41
26 45
46 30 52
35 88 72 Decrease 46 to 45.
M. S. Ramaiah School of Advanced Studies 56

57. Fibonacci Heap Operations
• FIB-HEAP-DECREASE-KEY(H; x; k)
– Case 2: parent of x is unmarked.
• decrease key of x to k
• cut off link between x and its parent
• mark parent
• add tree rooted at x to root list, updating heap min pointer
min
7 18 38
24 17 23 21 39 41
26 15
45 30 52
35 88 72 Decrease 45 to 15.
M. S. Ramaiah School of Advanced Studies 57

58. Fibonacci Heap Operations
• FIB-HEAP-DECREASE-KEY(H; x; k)
– Case 2: parent of x is unmarked.
• decrease key of x to k
• cut off link between x and its parent
• mark parent
• add tree rooted at x to root list, updating heap min pointer
min
7 18 38
24 17 23 21 39 41
26 45
15 30 52
35 88 72 Decrease 45 to 15.
M. S. Ramaiah School of Advanced Studies 58

59. Fibonacci Heap Operations
• FIB-HEAP-DECREASE-KEY(H; x; k)
– Case 2: parent of x is unmarked.
• decrease key of x to k
• cut off link between x and its parent
• mark parent
• add tree rooted at x to root list, updating heap min pointer
min
15 7 18 38
72 24 17 23 21 39 41
26 30 52
35 88
M. S. Ramaiah School of Advanced Studies 59

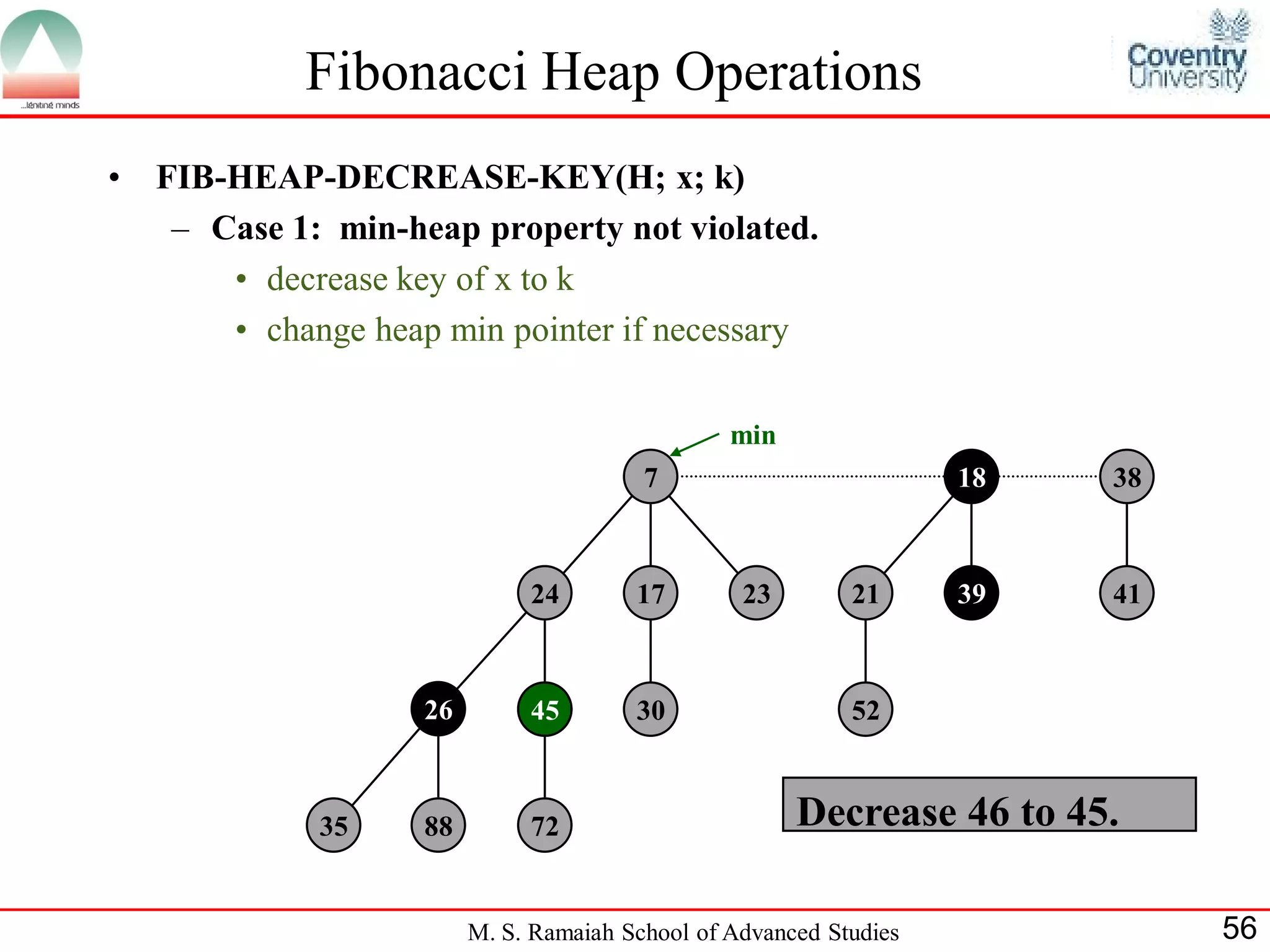
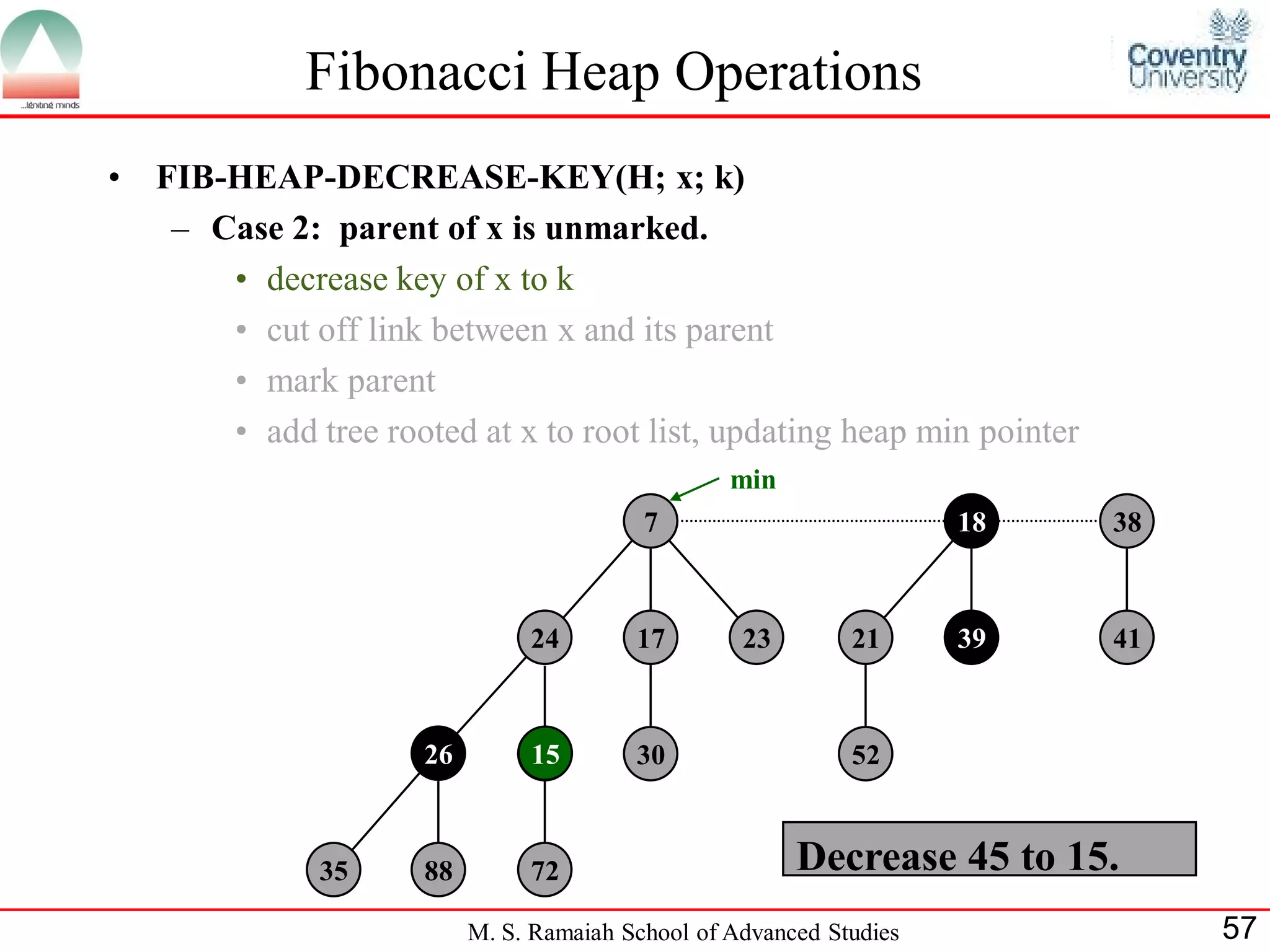
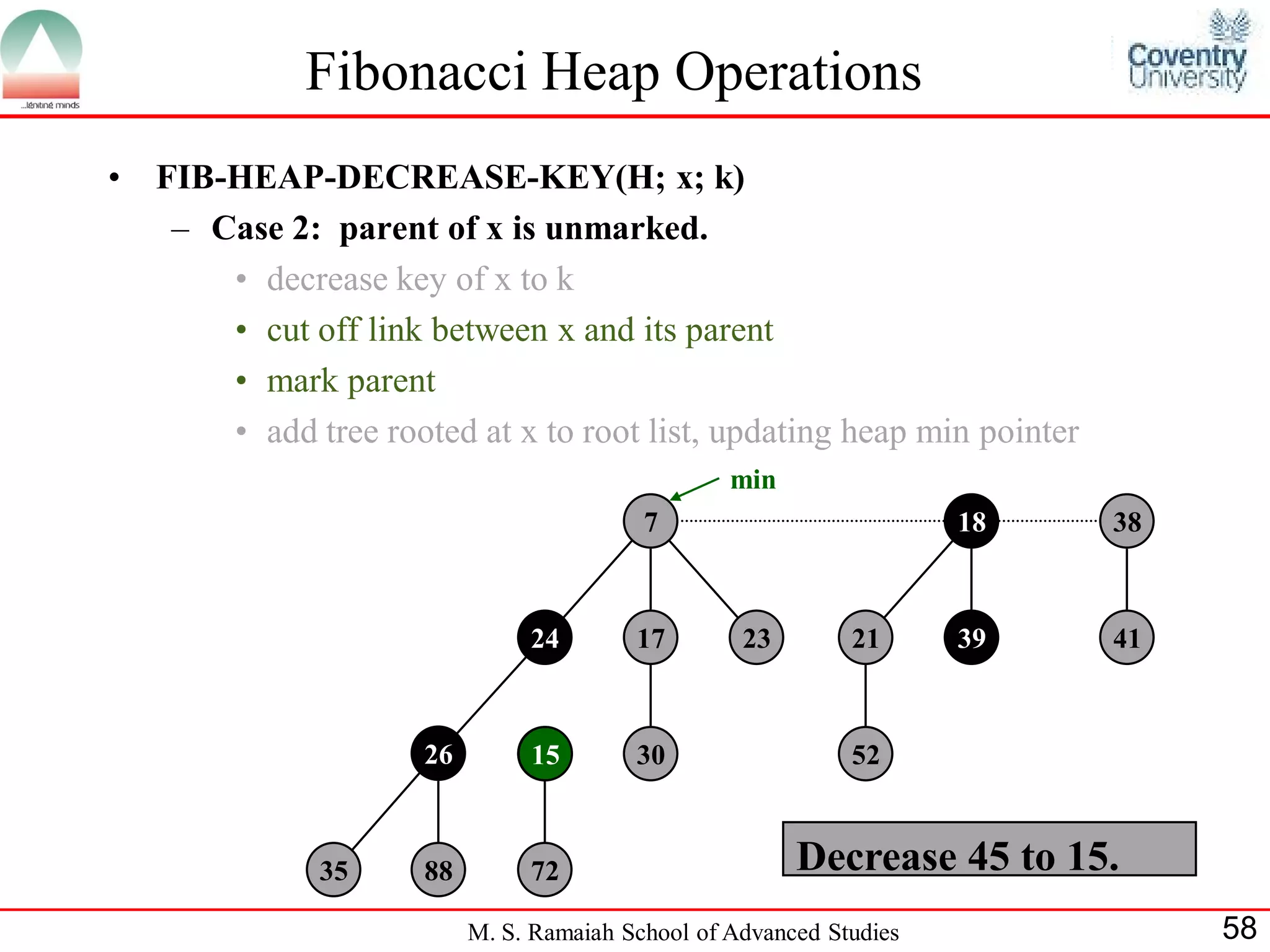
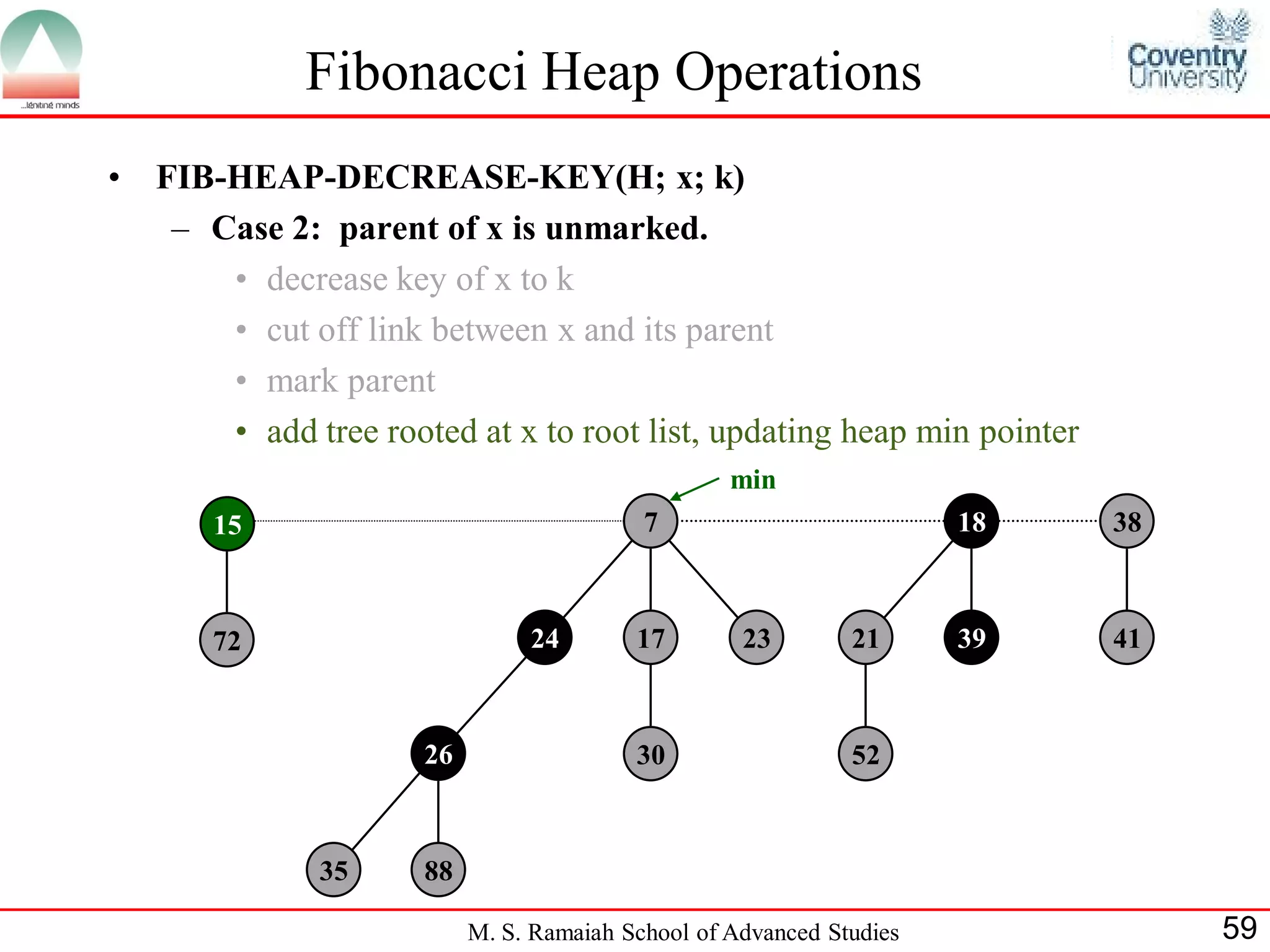
60. Fibonacci Heap Operations
• FIB-HEAP-DECREASE-KEY(H; x; k)
– Case 3: parent of x is marked.
• decrease key of x to k
• cut off link between x and its parent p[x], and add x to root list
• cut off link between p[x] and p[p[x]], add p[x] to root list
– If p[p[x]] unmarked, then mark it.
– If p[p[x]] marked, cut off p[p[x]], unmark, and repeat
min
15 7 18 38
72 24 17 23 21 39 41
26 30 52
35
5 88 Decrease 35 to 5.
M. S. Ramaiah School of Advanced Studies 60

61. Fibonacci Heap Operations
• FIB-HEAP-DECREASE-KEY(H; x; k)
– Case 3: parent of x is marked.
• decrease key of x to k
• cut off link between x and its parent p[x], and add x to root list
• cut off link between p[x] and p[p[x]], add p[x] to root list
– If p[p[x]] unmarked, then mark it.
– If p[p[x]] marked, cut off p[p[x]], unmark, and repeat
min
15 5 7 18 38
72 24 17 23 21 39 41
26 30 52
88 Decrease 35 to 5.
M. S. Ramaiah School of Advanced Studies 61

62. Fibonacci Heap Operations
• FIB-HEAP-DECREASE-KEY(H; x; k)
– Case 3: parent of x is marked.
• decrease key of x to k
• cut off link between x and its parent p[x], and add x to root list
• cut off link between p[x] and p[p[x]], add p[x] to root list
– If p[p[x]] unmarked, then mark it.
– If p[p[x]] marked, cut off p[p[x]], unmark, and repeat
min
15 5 26 7 18 38
72 88 24 17 23 21 39 41
30 52
Decrease 35 to 5.
M. S. Ramaiah School of Advanced Studies 62

63. Fibonacci Heap Operations
• FIB-HEAP-DECREASE-KEY(H; x; k)
– Case 3: parent of x is marked.
• decrease key of x to k
• cut off link between x and its parent p[x], and add x to root list
• cut off link between p[x] and p[p[x]], add p[x] to root list
– If p[p[x]] unmarked, then mark it.
– If p[p[x]] marked, cut off p[p[x]], unmark, and repeat
min
15 5 26 24 7 18 38
72 88 17 23 21 39 41
30 52
M. S. Ramaiah School of Advanced Studies 63

64. Fibonacci Heap Operations
FIB-HEAP-DECREASE-KEY(H; x; k) Analysis
• Notation.
– t(H) = # trees in heap H.
– m(H) = # marked nodes in heap H.
– (H) = t(H) + 2m(H).
• Actual cost. O(c)
– O(1) time for decrease key.
– O(1) time for each of c cascading cuts, plus reinserting in root list.
• Amortized cost. O(1)
– t(H') = t(H) + c
– m(H')  m(H) - c + 2
• each cascading cut unmark a node
• last cascading cut could potentially mark a node
–   c + 2(-c + 2) = 4 - c.
M. S. Ramaiah School of Advanced Studies 64

65. Fibonacci Heap Operations
FIB-HEAP-DELETE(H; x)
– Decrease key of x to -.
– Extract Min or Delete min element in heap.
6 2 1
5 3 4 7
8
9 Delete 9
M. S. Ramaiah School of Advanced Studies 65

66. Fibonacci Heap Operations
FIB-HEAP-DELETE(H; x)
– Decrease key of x to -.
– Extract Min or Delete min element in heap.
min
6 2 1
5 3 4 7
8
- Delete 9
M. S. Ramaiah School of Advanced Studies 66

67. Fibonacci Heap Operations
FIB-HEAP-DELETE(H; x)
– Decrease key of x to -.
– Extract Min or Delete min element in heap.
min
6 2 1 -
5 3 4 7
8
Delete 9
M. S. Ramaiah School of Advanced Studies 67

68. Fibonacci Heap Operations
FIB-HEAP-DELETE(H; x)
– Decrease key of x to -.
– Extract Min or Delete min element in heap.
min
6 2 1 - 8 7
5 3 4
Delete 9
M. S. Ramaiah School of Advanced Studies 68

69. Fibonacci Heap Operations
FIB-HEAP-DELETE(H; x)
– Decrease key of x to -.
– Extract Min or Delete min element in heap.
min
6 2 1 - 8 7
5 3 4
Delete 9
M. S. Ramaiah School of Advanced Studies 69

70. Fibonacci Heap Operations
FIB-HEAP-DELETE(H; x)
– Decrease key of x to -.
– Extract Min or Delete min element in heap.
min
6 1
2 3 4
5 7
8 Delete 9
M. S. Ramaiah School of Advanced Studies 70

71. Fibonacci Heap Operations
FIB-HEAP-DELETE(H; x) Analysis
• The amortized execution time of FIB-HEAP-DELETE(H; x) is the
sum of the amortized time of FIB-HEAP-DECREASE i.e. O(1) and
the amortized time of FIB-HEAP-EXTRACT-MIN(H) i.e. O(D(n))
M. S. Ramaiah School of Advanced Studies 71

72. Conclusion
• Fibonacci heap is a heap data structure consisting of collection of trees.
• It has a better amortized running time of binomial heap.
• It improve Dijkstra's shortest path algorithm
from O(E log V ) to O(E + V log V ).
• It is a heap ordered trees with the minimum node pointed to by a
pointer and some nodes marked.
• Fibonacci heap takes a amortized time of O(1) for make heap, insert,
find min ,union , decrease key and is empty operations and a O(log n)
amortized time for delete-min and delete operation.
M. S. Ramaiah School of Advanced Studies 72

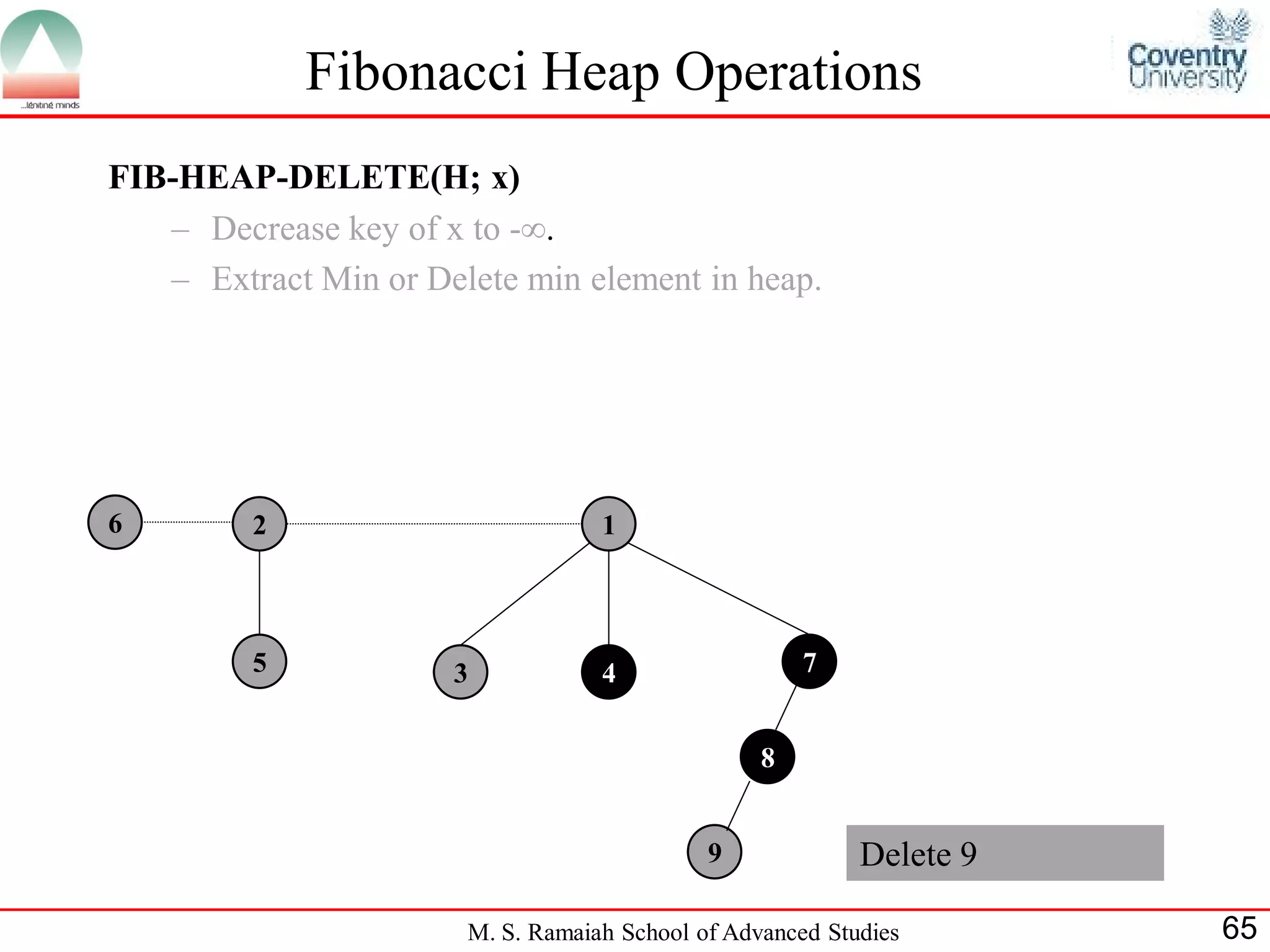
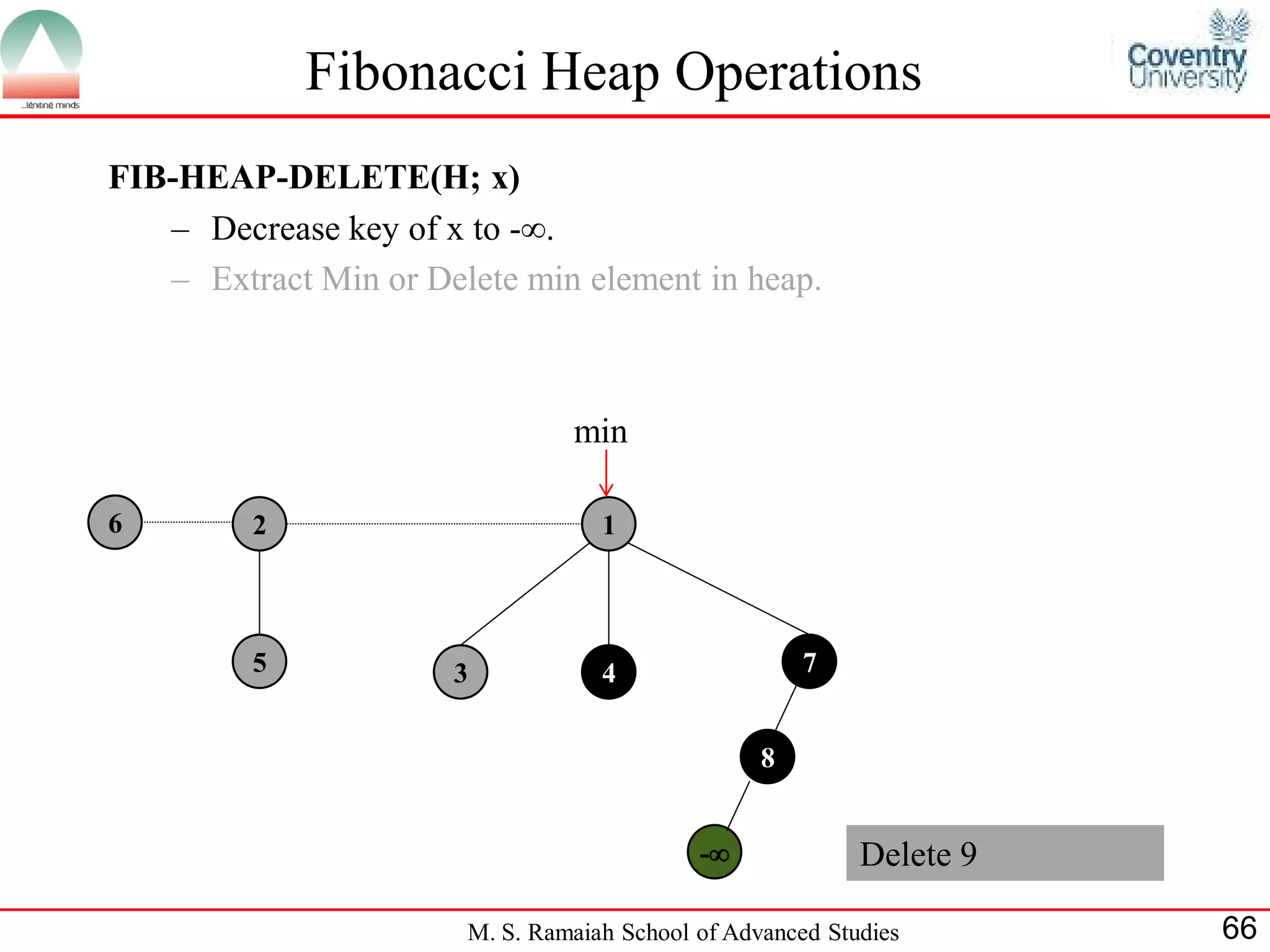
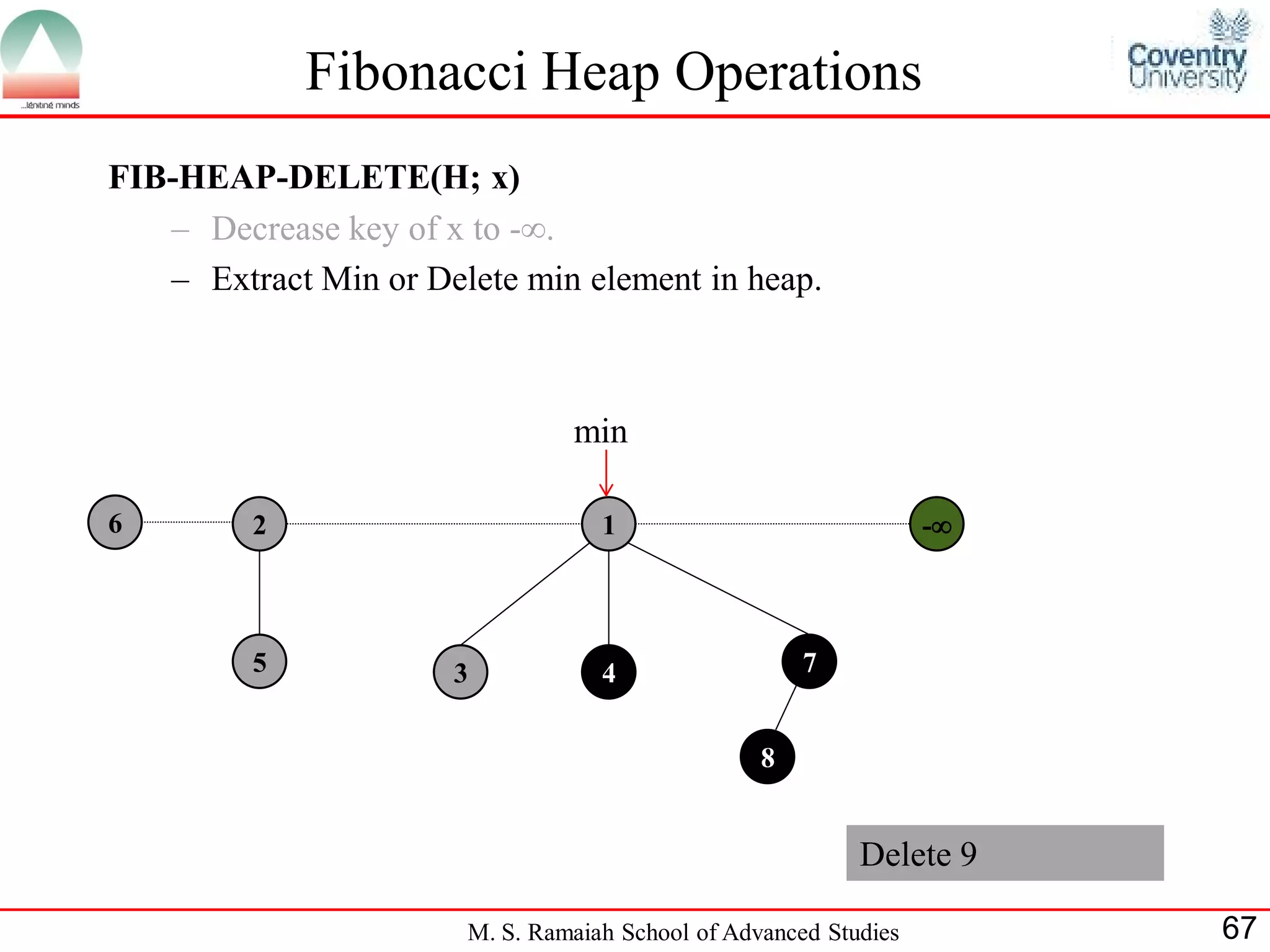
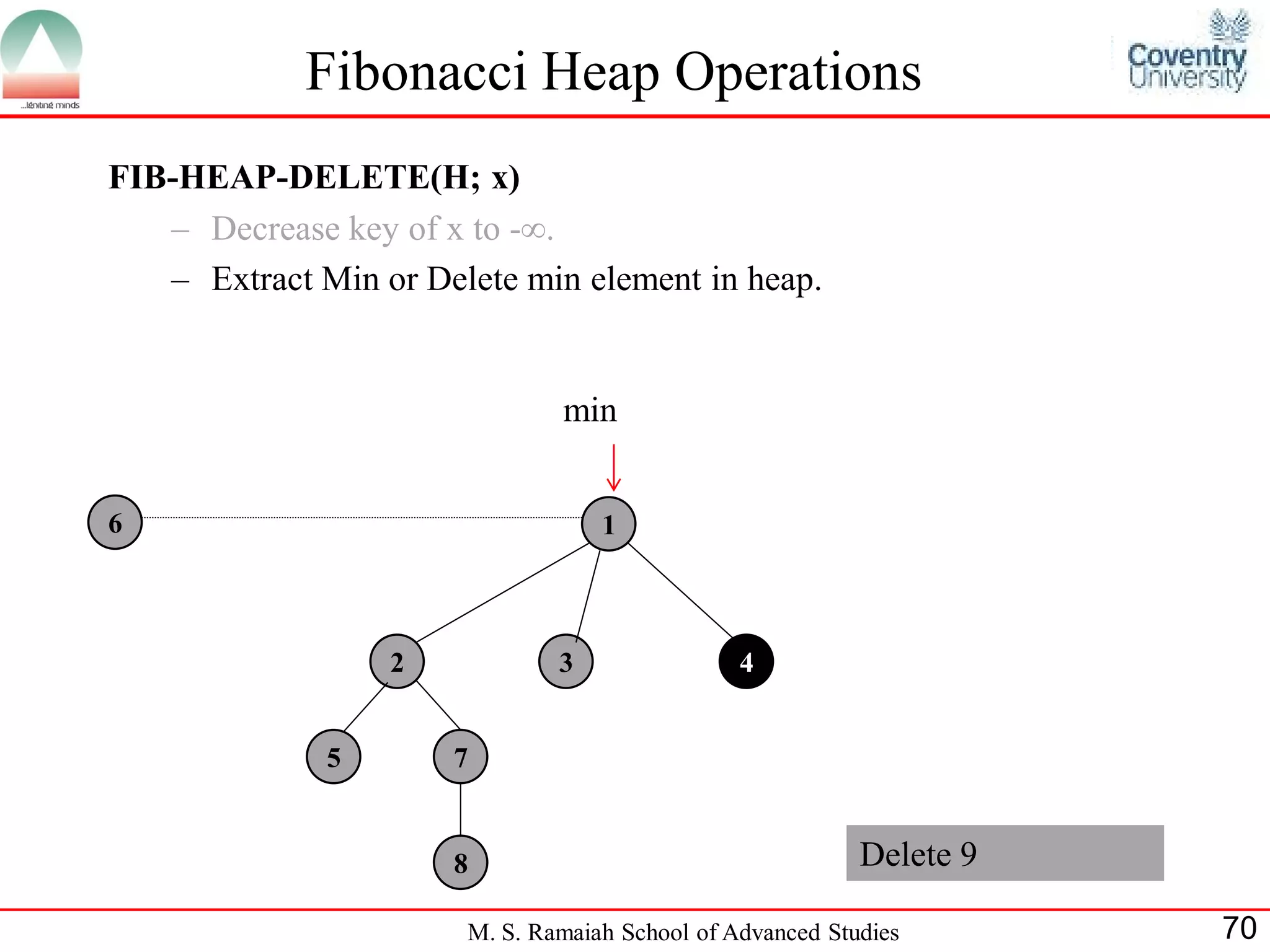
73. References
[1] Cormen T.H, Leiserson C.E., Rivest R.L., and Stein
C,(2009),IntroductiontoAlgorithms,3rdedn,NewDelhi:
Prentice Hall of India
[2] Fredman M and Tarjan R.E.,(July 1987), Fibonacci Heaps
and Their Uses in Improved Network Optimization
Algorithms. Journal of the Association for Computing
Machinery, Vol. 34, No. 3, July 1987, Pages 596-615.
M. S. Ramaiah School of Advanced Studies 73