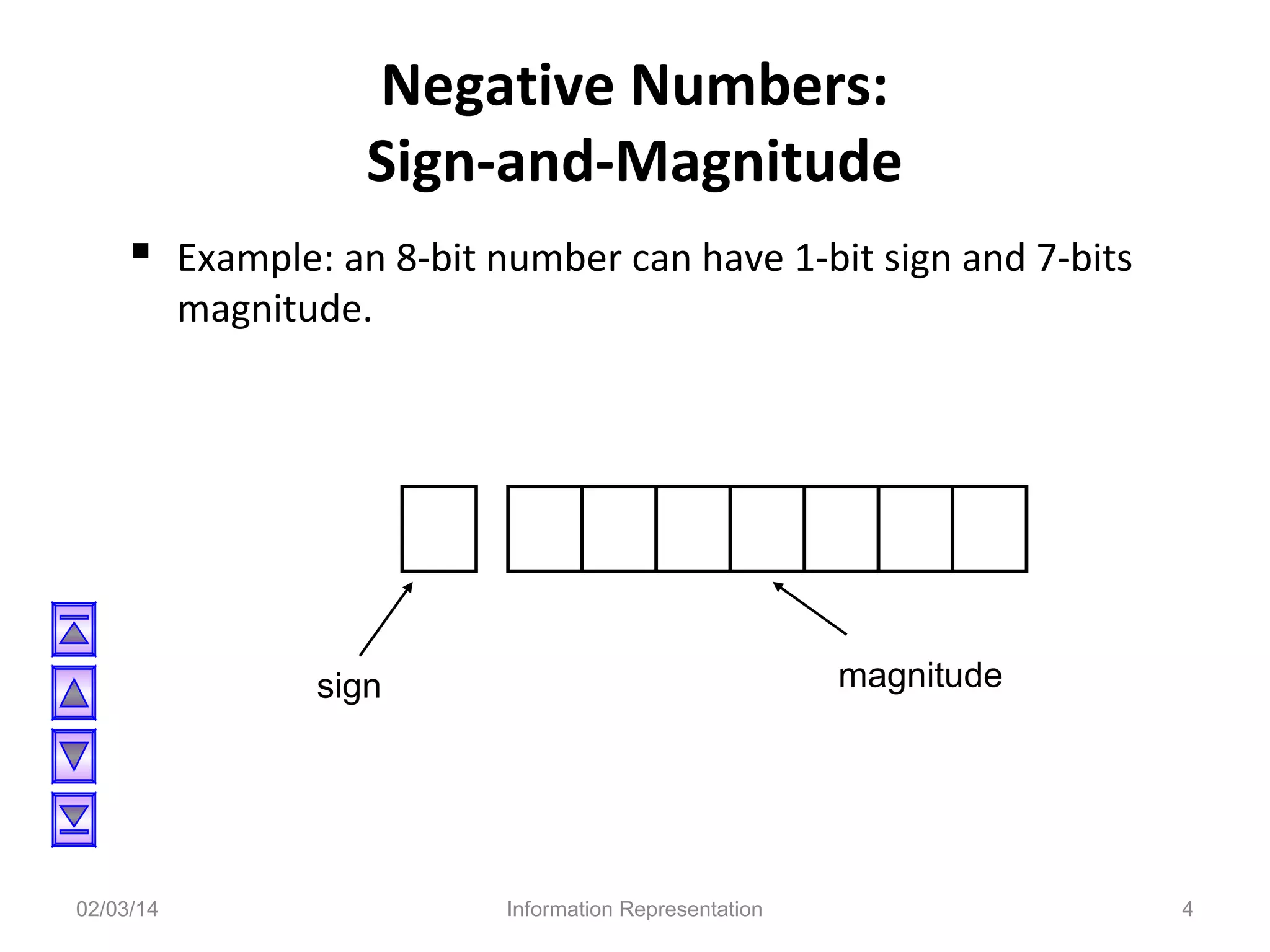
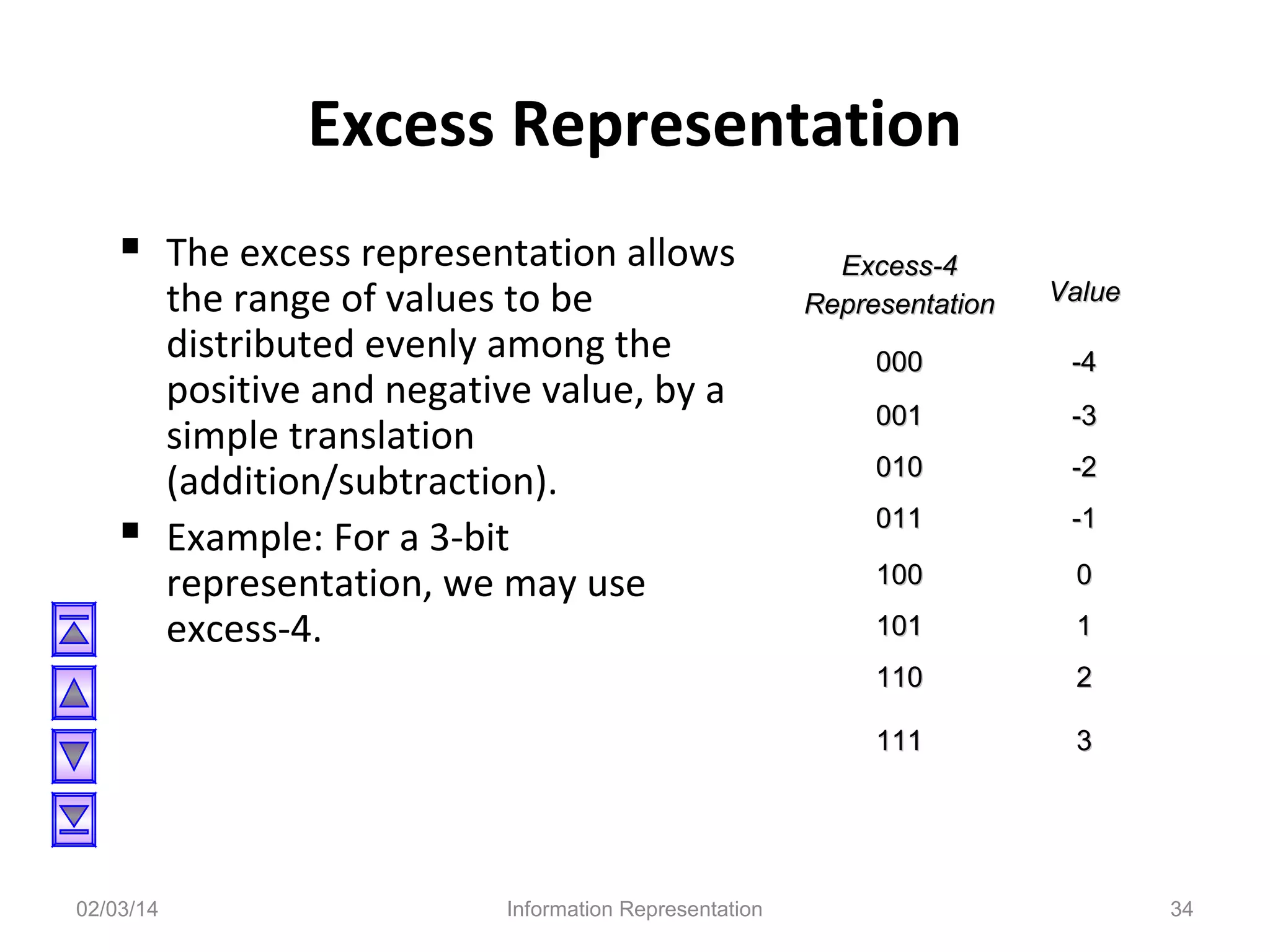
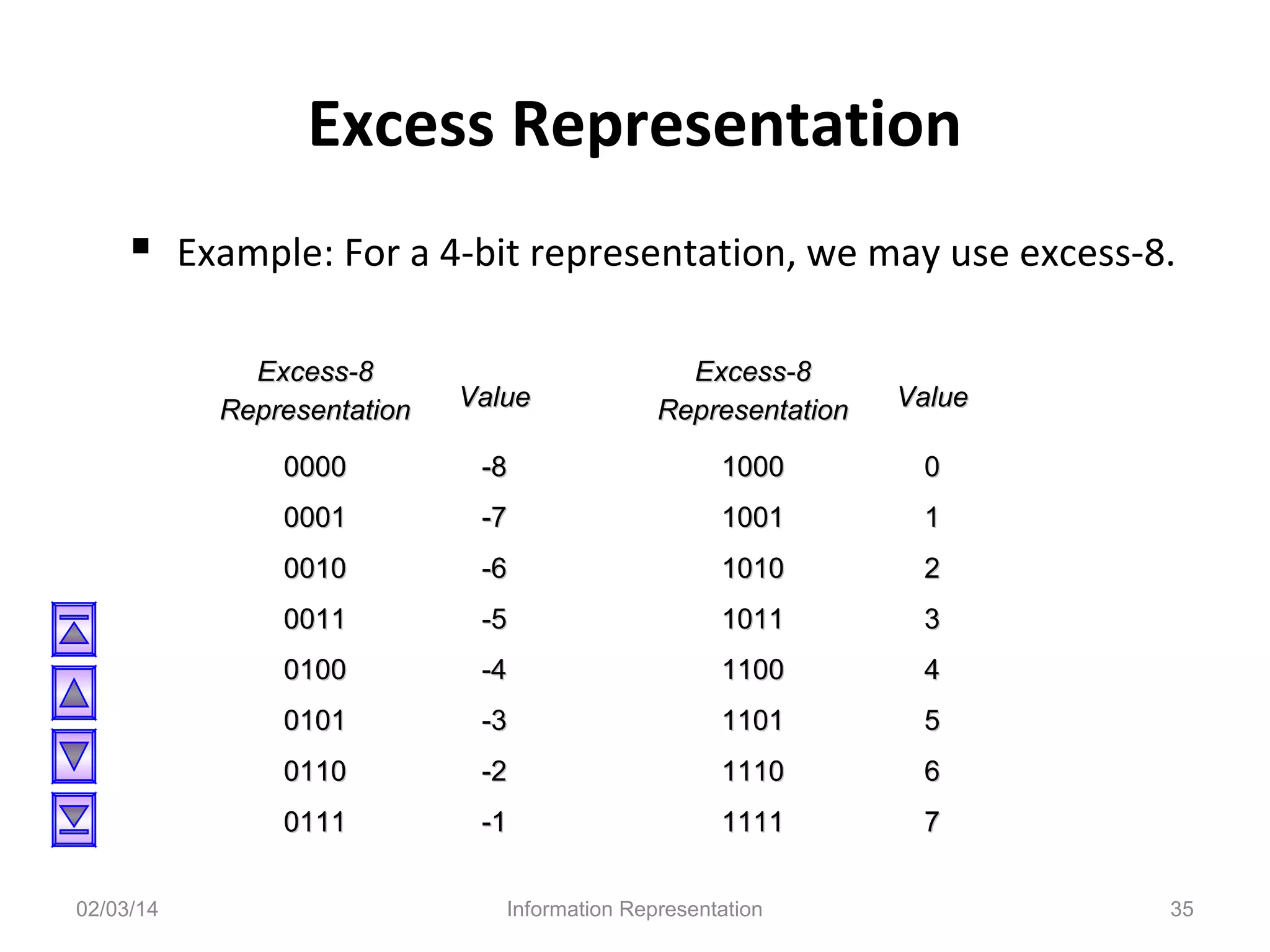
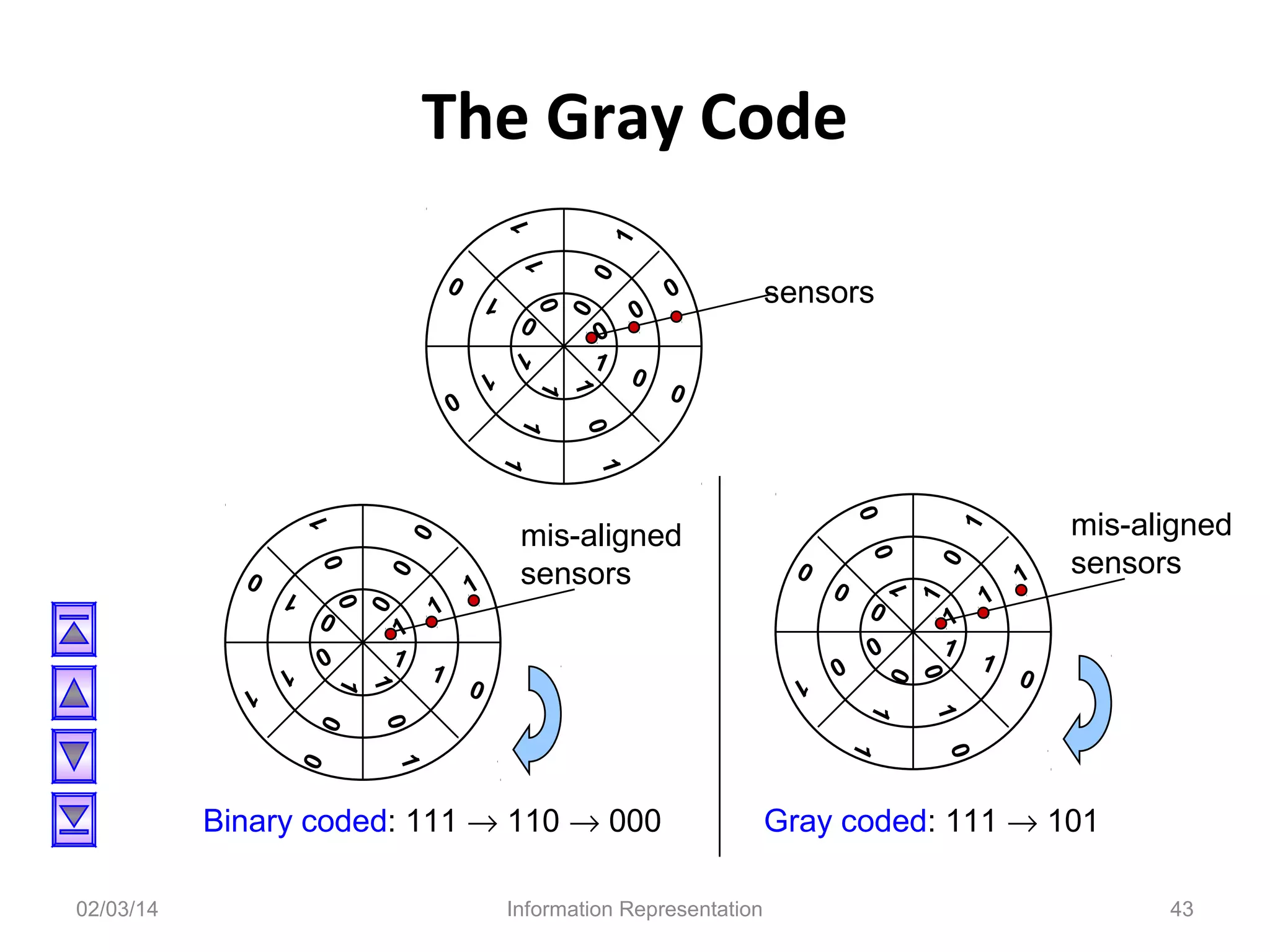
The document discusses various methods for representing negative numbers in binary, including sign-and-magnitude, 1's complement, and 2's complement representations. It explains each method in detail, providing examples of how positive and negative numbers are represented. It also covers related topics like overflow, fixed-point versus floating-point number representations, and excess representation of exponents in floating-point numbers.
















![Diminished-Radix Complements
Given an n-digit number, xr, its (r-1)’s complement is:
(rn - 1) - x
E.g.: (r-1)’s complement, or 9s complement, of (22)10 is:
(102 - 1) - 22 = (77)9s [This means –(22)10 is (77)9s]
(r-1)’s complement, or 1s complement, of (0101)2 is:
(24- 1) - 0101 = (1010)1s [This means –(0101)2 is (1010)1s]
Same as inverting all digits:
(102 - 1) - 22 = 99 - 22 = (77)9s
(24 - 1) - 0101 = 1111 - 0101 = (1010)1s
02/03/14
Information Representation
18](https://image.slidesharecdn.com/lecture3-140203103531-phpapp02/75/Lecture-3-18-2048.jpg)
![Radix Complements
Given an n-digit number, xr, its r’s-complement is:
rn - x
E.g.: r’s-complement, or 10s complement, of (22)10 is:
102 - 22 = (78)10s [This means –(22)10 is (78)10s]
r’s-complement, or 2s complement, of (0101)2 is:
24 - 0101 = (1011)2s [This means –(0101)2 is (1011)2s]
Same as inverting all digits and adding 1:
(102) - 22 = (99+1) - 22
= 77 + 1 = (78)10s
(24) - 0101 = (1111+1) - 0101 = 1010 +1 = (1011)2s
02/03/14
Information Representation
19](https://image.slidesharecdn.com/lecture3-140203103531-phpapp02/75/Lecture-3-19-2048.jpg)



























![Alphanumeric Codes
ASCII table:
LSBs
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
02/03/14
000
NUL
SOH
STX
ETX
EOT
ENQ
ACK
BEL
BS
HT
LF
VT
FF
CR
O
SI
001
DLE
DC1
DC2
DC3
DC4
NAK
SYN
ETB
CAN
EM
SUB
ESC
FS
GS
RS
US
010
SP
!
“
#
$
%
&
‘
(
)
*
+
,
.
/
MSBs
011 100
0
@
1
A
2
B
3
C
4
D
5
E
6
F
7
G
8
H
9
I
:
J
;
K
<
L
=
M
>
N
?
O
Information Representation
101
P
Q
R
S
T
U
V
W
X
Y
Z
[
]
^
_
110
`
a
b
c
d
e
f
g
h
i
j
k
l
m
n
o
111
p
q
r
s
t
u
v
w
x
y
z
{
|
}
~
DEL
50](https://image.slidesharecdn.com/lecture3-140203103531-phpapp02/75/Lecture-3-50-2048.jpg)



