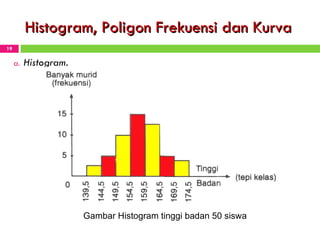
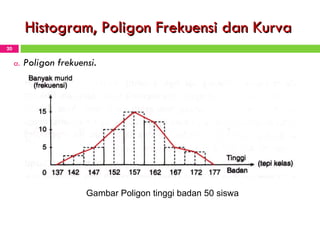
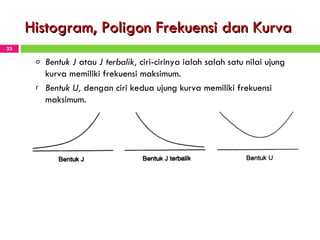
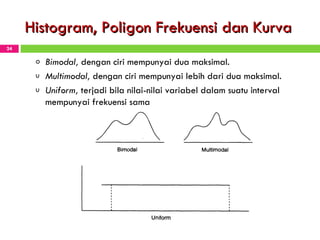
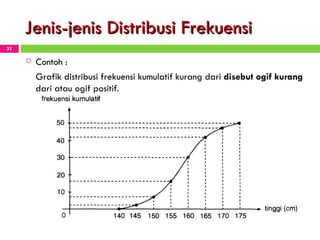
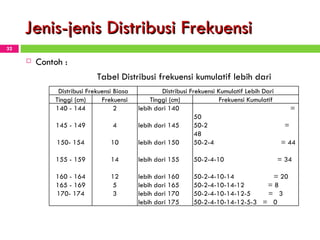
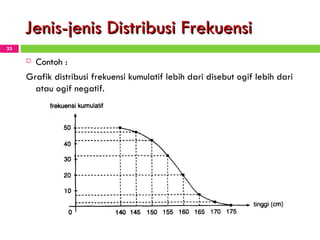
Dokumen tersebut membahas tentang statistika dan penyajian data. Secara singkat, dokumen tersebut menjelaskan bagaimana mahasiswa dapat mengolah data mentah menjadi tabel dan gambar seperti histogram, diagram batang, dan kurva ogive untuk menyajikan data secara sistematis dan menarik.

1. S TATISTIKA I Disusun : Ir. Tri Mulyanto, MT KELAS 2EA21

2. H asil Pembelajaran Pokok Bahasan Penyajian Data . Sub Pokok Bahasan : Pembentukan Tabel Frekuensi . Frekuensi relatif dan kumulatif . Pembuatan Histogram, Diagram Batang, Polygon, Kurva Ogive, Diagram Pie. TIU: M a h a s iswa mampu menyajikan data dalam bentuk tabel dan gambar . Sasaran belajar M a h a s iswa dapat mengolah data mentah menjadi bentuk tabel, dapat menentukan interval kelas dan batas kelas sesuai kebutuhan dan menyajikan data secara menarik. M a h a s iswa dapat menghitung frek. relatif dan kumulatif serta memahami saat pemakaiannya. M a h a s iswa mampu mengolah data menjadi bentuk gambar .

3. Pengertian Data yang telah diperoleh dari suatu penelitian yang masih berupa data acak atau data mentah dapat dibuat menjadi data yang berkelompok, yaitu data yang telah disusun ke dalam kelas-kelas tertentu. Daftar yang memuat data berkelompok disebut distribusi frekuensi atau t abel frekuensi. Jadi, distribusi frekuensi adalah susunan data menurut kelas-kelas interval tertentu atau menurut kategori tertentu dalam sebuah daftar. Dari distribusi frekuensi, dapat diperoleh keterangan atau gambaran sederhana dan sistematis dari data yang diperoleh.

4. Bagian Distribusi Frekuensi (1) 1) Kelas-kelas (class) Kelas adalah kelompok nilai data atau variabel. 2) Batas kelas (class limits) Batas kelas adalah nilai-nilai yang membatasi kelas yang satu dengan kelas yang lain. Terdapat dua batas kelas, yaitu: batas kelas bawah (lower class limits), terdapat di deretan sebelah kiri setiap kelas; batas kelas atas (upper class limits), terdapat di deretan sebelah kanan setiap kelas. Batas kelas merupakan batas semu dari setiap kelas, karena di antara kelas yang satu dengan kelas yang lain masih terdapat lubang tempat angka-angka tertentu.

5. Bagian Distribusi Frekuensi (2) 3) Tepi kelas (class boundary/real limits/true class limits) Tepi kelas disebut juga batas nyata kelas, yaitu batas kelas yang tidak memiliki lubang untuk angka tertentu antara kelas yang satu dengan kelas yang lain. Terdapat dua tepi kelas, yaitu: a) tepi bawah kelas atau batas kelas bawah sebenarnya; b) tepi atas kelas atau batas kelas atas sebenarnya. Penentuan tepi bawah kelas dan tepi atas kelas bergantung pada keakuratan pencatatan data. Misalnya, data dicatat dengan ketelitian sampai satu desimal, maka rumus tepi bawah kelas dan tepi atas kelas ialah sebagai berikut. a) tepi bawah kelas = batas bawah kelas - 0,5; b) tepi atas kelas = batas atas kelas + 0,5.

6. Bagian Distribusi Frekuensi (3) 4) Titik tengah kelas / tanda kelas ( class mid point, class marks ) Titik tengah kelas adalah angka atau nilai data yang tepat terletak di tengah suatu kelas. Titik tengah kelas merupakan nilai yang mewakili kelasnya. Titik tengah kelas = ½ ( batas atas + batas bawah) kelas. 5) Interval kelas (class interval) Interval kelas adalah selang yang memisahkan ke l as yang satu dengan kelas yang lain. 6) Panjang interval kelas atau luas kelas (interval size) Panjang interval kelas adalah jarak antara tepi atas kelas dan tepi bawah kelas. 7) Frekuensi kelas (class frequency) Frekuensi kelas adalah banyaknya data yang termasuk ke dalam kelas tertentu.

7. Bagian Distribusi Frekuensi (4) Contoh: T abel M odal perusahaan PT. "X" Dari distribusi frekuensi di atas: 1. Banyaknya kelas adalah 5. 2. Batas kelas-kelas adalah 50, 59, 60, 69, .... 3. Batas bawah kelas-kelas adalah 50, 60, 70, 80, 90. 4. Batas atas kelas-kelas adalah 59, 69, 79, 89, 99. 5. Batas nyata kelas-kelas adalah 49,5; 59,5; 69,5; 79,5 .... 6. T epi bawah kelas-kelas adalah 49,5; 59,5; 69,5; 79,5; 89,5. 7. Tepi atas kelas-kelas adalah 59,5; 69,5; 79,5; 89,5; 99,5. 8. Titik tengah kelas-kelas adalah 54,5; 64,5; 74,5; 84,5; .... 9. Interval kelas-kelas adalah 50 - 59, 60 - 69, ..., 90 - 99. 10 . Panjang interval kelas-kelas masing-masing 10. 11. Frekuensi kelas-kelas adalah 16, 32, 20, 17, dan 15. Modal (jutaan Rp) Frekuensi ( f ) 50-59 16 60-69 32 70-79 20 80- 89 17 90-99 15 Jumlah 100

8. Bagian Distribusi Frekuensi (5) Beberapa catatan mengenai distribusi frekuensi Kadang-kadang suatu distribusi memiliki panjang interval kelas yang tidak sama, bergantung kepada tujuannya. Kadang-kadang distribusi frekuensi memiliki batas kelas yang berulang, suatu nilai (batas kelas) dipakai sebagai dua batas kelas. K adang-kadang distribusi frekuensi memiliki kelas terbuka, artinya batas kelas atas pada kelas terakhir dan batas kelas bawah pada kelas pertama tidak ada.

9. Penyusunan Distribusi Frekuensi (1) Distribusi frekuensi dapat dibuat dgn mengikuti pedoman berikut. Mengurutkan data dari yang terkecil ke yang terbesar. Menentukan jangkauan (range) dari data. J angkauan = data terbesar - data terkecil. Menentukan banyaknya kelas (k). Banyaknya kelas ditentukan dengan rumus sturgess Keterangan: k = banyaknya kelas n = banyaknya data Hasilnya dibulatkan, biasanya ke atas. k  bulat

10. Penyusunan Distribusi Frekuensi (2) Menentukan panjang interval kelas. Panjang interval kelas ( i ) = Menentukan batas bawah kelas pertama. Batas bawah kelas pertama biasanya dipilih dari data terkecil atau data terkecil yang berasal dari pelebaran jangkauan (data yang lebih kecil dari data terkecil) dan selisihnya harus kurang dari panjang interval kelasnya. Menuliskan frekuensi kelas secara melidi dalam kolom turns atau tally (sistem turns) sesuai banyaknya data.

11. Penyusunan Distribusi Frekuensi (3) Beberapa catatan tentang penyusunan distribusi frekuensi Pada pembuatan distribusi frekuensi, perlu dijaga jangan sampai ada data yang tidak dimasukkan ke dalam kelas atau ada data yang masuk ke dalam dua kelas yang berbeda. Titik tengah kelas diusahakan bilangan bulat/tidak pecahan. Nilai frekuensi diusahakan tidak ada yang nol. Dalam menentukan banyaknya kelas (k), diusahakan : tidak terlalu sedikit, sehingga pola kelompok kabur; banyaknya kelas berkisar 5 sampai 15 buah; jika jangkauan terlalu besar maka banyaknya kelas antara 10 sampai 20.

12. Penyusunan Distribusi Frekuensi (4) Cara lain dalam menetapkan banyaknya kelas ialah: memilih atau menetapkannya sesuai dengan kebutuhan yang diinginkan; menggunakan rumus : Keterangan: R = jangkauan i = panjang interval kelas Cara tersebut dipakai dengan mencoba menetapkan terlebih dahulu panjang interval kelasnya ( i ).

13. Penyusunan Distribusi Frekuensi (5) Contoh soal: Dari hasil pengukuran diameter pipa-pipa yang dibuat oleh sebuah mesin (dalam mm terdekat), diperoleh data sebagai berikut. Buatlah distribusi frekuensi dari data tersebut! 78 72 74 79 74 71 75 74 72 68 72 73 72 74 75 74 73 74 65 72 66 75 80 69 82 73 74 72 79 71 70 75 71 70 70 70 75 76 77 67

14. Penyusunan Distribusi Frekuensi (6) Penyelesaian: Urutan data: Jangkauan ( R ) = 82 – 65 = 17 Banyaknya kelas (k) adalah K = 1 + 3,3 log 40 = 1 + 5,3 = 6,3 Panjang interval kelas (i) adalah : Batas kelas pertama adalah 65 (data terkecil) 65 66 67 68 69 70 70 70 70 71 71 71 72 72 72 72 72 72 73 73 73 74 74 74 74 74 74 74 75 75 75 75 75 76 77 78 79 79 80 82

15. Penyusunan Distribusi Frekuensi (7) Tabelnya Tabel : Pengukuran Diameter pipa-pipa (satuan mm) Diameter Tarus/Tally Frekuensi 65 -67 III 3 68-70 IIII I 6 71 -73 IIII IIII II 12 74-76 IIII IIII I II 13 77-79 IIII 4 80- 82 II 2 Jumlah 40

16. Penyusunan Distribusi Frekuensi (8) Latihan Soal : Berikut ini data mengenai jumlah modal (dalam jutaan Rp) dari 50 orang pada perusahaan "X" Buatlah distribusi frekuensi dari data tersebut! 80 18 69 51 71 92 35 28 60 45 63 59 64 98 47 49 48 64 58 74 85 56 72 38 89 55 28 67 84 78 37 73 65 66 86 96 57 76 57 19 54 76 49 53 83 55 83 47 64 39

17. Histogram, Poligon Frekuensi dan Kurva 1. Histogram dan Poligon Frekuensi Histogram dan poligon frekuensi adalah dua grafik yang sering digunakan untuk menggambarkan distribusi frekuensi. Histogram merupakan grafik batang dari distribusi frekuensi dan poligon frekuensi merupakan grafik garisnya. Pada histogram, batang-batangnya saling melekat atau berimpitan, sedang poligon frekuensi dibuat dengan cara menarik garis dari satu titik tengah batang histogram ke titik tengah batang histogram yang lain. Agar diperoleh poligon tertutup, ha ru s dibuat dua kelas baru dengan panjang kelas sama dengan frekuensi nol pada kedua ujungnya. Pembuatan dua kelas baru itu diperbolehkan karena luas histogram dan poligon yang tertutup sama.

18. Histogram, Poligon Frekuensi dan Kurva Pada pembuatan histogram digunakan sistem salib sumbu. Sumbu mendatar (sumbu X) menyatakan interval kelas (tepi bawah dan tepi atas masing-masing kelas) dan sumbu tegak (sumbu Y) menyatakan frekuensi. Contoh : Tabel D istribusi F rekuensi hasil pengukuran tinggi badan 50 siswa. Interval Kelas Tu rus / Frekuensi Tepi Interval Titik Tengah (Tinggi (cm)) Tally (Banyak Murid) Kelas 140 - 144 II 2 139,5 - 144,5 142 145 - 149 IIII 4 144,5 - 149,5 147 150 - 154 IIII IIII 10 149,5 - 154,5 152 155 - 159 IIII IIII IIII 14 154,5 - 159,5 157 160 - 164 IIII IIII II 12 159,5 - 164,5 162 165 - 169 IIII 5 164,5 - 169,5 167 170 - 174 III 3 169,5 - 174,5 172  f = 50

19. Histogram, Poligon Frekuensi dan Kurva Histogram . Gambar Histogram tinggi badan 50 siswa

20. Histogram, Poligon Frekuensi dan Kurva Poligon frekuensi . Gambar Poligon tinggi badan 50 siswa

21. Histogram, Poligon Frekuensi dan Kurva 2 . Kurva Frekuensi Kurva distribusi frekuensi, disingkat kurva frekuensi yang telah dihaluskan mempunyai berbagai bentuk dengan ciri-ciri tertentu. Bentuk-bentuk kurva frekuensi adalah sebagai berikut. Simetris atau berbentuk lonceng, ciri-cirinya ialah nilai variabel di samping kiri dan kanan yang berjarak sama terhadap titik tengah (yang frekuensinya terbesar) mempunyai frekuensi yang sama. Bentuk kurva simetris sering dijumpai dalam distribusi bermacam-macam variabel, karena itu dinamakan distribusi normal.

22. Histogram, Poligon Frekuensi dan Kurva Tidak simetris atau condong, ciri-cirinya ialah ekor kurva yang satu lebih panjang daripada ekor kurva lainnya. Jika ekor kurva lebih panjang berada di sebelah kanan kurva disebut kurva condong ke kanan (mempunyai kecondongan positif), sebaliknya disebut condong ke kiri (mempunyai kecondongan negatif).

23. Histogram, Poligon Frekuensi dan Kurva Bentuk J atau J terbalik, ciri-cirinya ialah salah satu nilai ujung kurva memiliki frekuensi maksimum. B entuk U, dengan ciri kedua ujung kurva memiliki frekuensi maksimum.

24. Histogram, Poligon Frekuensi dan Kurva Bimodal, dengan ciri mempunyai dua maksimal. Multimodal, dengan ciri mempunyai lebih dari dua maksimal. Uniform, terjadi bila nilai-nilai variabel dalam suatu interval mempunyai frekuensi sama

25. Jenis-jenis Distribusi Frekuensi 1. Distribusi Frekuensi Biasa Distribusi frekuensi biasa adalah distribusi frekuensi yang hanya berisikan jumlah frekuensi dari setiap kelompok data atau kelas. Ada dua jenis distribusi frekuensi biasa, yaitu distribusi frekuensi numerik dan distribusi frekuensi peristiwa atau kategori. a. Distribusi frekuensi numerik Distribusi frekuensi numerik adalah distribusi frekuensi yang pembagian kelasnya dinyatakan dalam angka. T abel P elamar P erusahaan "XYZ", 1990 Umur (tahun) Frekuensi 20-24 15 25-29 20 30- 34 9 35-39 4 40-44 2 Jumlah 50

26. Jenis-jenis Distribusi Frekuensi b . Distribusi frekuensi peristiwa atau kategori Distribusi f rekuensi peristiwa atau kategori adalah distribusi frekuensi yang pembagian kelasnya dinyatakan berdasarkan data atau golongan data yang ada. T abel Hasil pelemparan dadu sebanyak 30 kali Angka Dadu (X) Banyaknya Peristiwa ( f ) 1 4 2 6 3 5 4 3 5 8 6 4 Jumlah 30

27. Jenis-jenis Distribusi Frekuensi 2 . Distribusi Frekuensi Relatif Distribusi frekuensi relatif adalah distribusi frekuensi yang berisikan nilai-nilai hasil bagi antara frekuensi kelas dan jumlah pengamatan yang terkandung dalam kumpulan data yang berdistribusi tertentu. Pada distribusi frekuensi relatif ini, frekuensi relatifnya dirumuskan Misalkan distribusi frekuensi memiliki k buah interval kelas dengan frekuensi masing-masing: f 1 , f 2 , . . ., f k maka distribusi yang terbentuk adalah : Interval kelas Frekuensi Frekuensi relatif Interval kelas ke-1 f 1 Interval kelas ke-2 f 2 • • • • • • • • • Interval kelas ke -k f k Jumlah  f =n

28. Jenis-jenis Distribusi Frekuensi 2 . Distribusi Frekuensi Relatif F rekuensi relatif kadang-kadang dinyatakan dalam bentuk perbandingan desimal, ataupun persen . Contoh : Tabel Distribusi frekuensi relatif. Interval Kelas (Tinggi (cm)) Frekuensi (Banyak Murid) Frekuensi Relatif Perbandingan Desimal Persen 140 - 144 2 2 / 50 0,04 4 145 - 149 4 4 / 50 0,08 8 150 - 154 10 10 / 50 0,20 20 155 - 159 14 14 / 50 0,28 28 160 - 164 12 12 / 50 0,24 24 165 - 169 5 5 / 50 0,10 10 170 - 174 3 3 / 50 0,06 6 Jumlah 50 1 1 100

29. Jenis-jenis Distribusi Frekuensi 3 . Distribusi Frekuensi Kumulatif Distribusi frekuensi kumulatif adalah distribusi frekuensi yang berisikan frekuensi kumulatif. Frekuensi kumulatif adalah frekuensi yang dijumlahkan. Distribusi frekuensi kumulatif memiliki grafik atau kurva yang disebut ogif . Pada ogif dicantumkan frekuensi kumulatifnya dan digunakan nilai batas kelas. Ada dua macam distribusi frekuensi kumulatif, yaitu distribusi frekuensi kumulatif kurang dari dan lebih dari. a. Distribusi frekuensi kumulatif kurang dari Distribusi frekuensi kumulatif kurang dari adalah distribusi frekuensi yang memuat jurnlah frekuensi yang memiliki nilai kurang dari nilai batas kelas suatu interval tertentu.

30. Jenis-jenis Distribusi Frekuensi b. Distribusi frekuensi kum ul atif lebih dari Distribusi frekuensi kumuiatif lebih dari adalah distribusi frekuensi yang memuat jurnlah frekuensi yang memiliki nilai lebih dari nilai batas kelas suatu interval tertentu Contoh : Tabel Distribusi Frekuensi kumulatif kurang dari Distribusi Frekuensi Biasa Distribusi Frekuensi Kumulatif Kurang Dari Tinggi (cm) Frekuensi Tinggi (cm) Frekuensi Kumulatif kurang dari 140 = 0 140 - 144 2 kurang dari 145 0 + 2 = 2 145 - 149 4 kurang dari 150 0+2+4 = 6 150 - 154 10 kurang dari 155 0 + 2 + 4+10 = 16 155 - 159 14 kurang dari 160 0 + 2 + 4 + 10+14 = 30 160 - 164 12 kurang dari 165 0 + 2 + 4 + 10+14+12 = 42 165 - 169 5 kurang dari 170 0 + 2 + 4+10+14 + 12 + 5 = 47 170 - 174 3 kurang dari 175 0 + 2 + 4+10+14+12 + 5 + 3 = 50

31. Jenis-jenis Distribusi Frekuensi Contoh : Grafik distribusi frekuensi kumulatif kurang dari disebut ogif kurang dari atau ogif positif.

32. Jenis-jenis Distribusi Frekuensi Contoh : Tabel Distribusi frekuensi kumulatif lebih dari Distribusi Frekuensi Biasa Distribusi Frekuensi Kumulatif Lebih Dari Tinggi (cm) Frekuensi Tinggi (cm) Frekuensi Kumulatif 140 - 144 2 lebih dari 140 = 50 145 - 149 4 lebih dari 145 50-2 = 48 150- 154 10 lebih dari 150 50-2-4 = 44 155 - 159 14 lebih dari 155 50-2-4-10 = 34 160 - 164 12 lebih dari 160 50-2-4-10-14 = 20 165 - 169 5 lebih dari 165 50-2-4-10-14-12 = 8 170- 174 3 lebih dari 170 50-2-4-10-14-12-5 = 3 lebih dari 175 50-2-4-10-14-12-5-3 = 0

33. Jenis-jenis Distribusi Frekuensi Contoh : Grafik distribusi frekuensi kumulatif lebih dari disebut ogif lebih dari atau ogif negatif.

34. Jenis-jenis Distribusi Frekuensi Contoh soal: Berikut adalah data 50 mahasiswa dalam perolehan nilai statistika pada FE U”X” semester II tahun 2007. Berapa orang yang mendapat nilai antara 44-52 dan 80-88 Berapa % orang yang mendapat nilai antara 53-61 ndan 89-97. Berapa banyak orang yang nilainya kurang dari 44. Berapa banyak orang yang nilainya kurang dari 71. 7 0 91 93 82 78 70 71 92 38 56 7 9 49 48 74 81 95 87 80 80 84 35 83 73 74 43 86 68 92 93 76 81 70 74 97 95 80 53 71 77 63 74 73 68 72 85 57 65 93 83 86

35. Jenis-jenis Distribusi Frekuensi Penyelesaian : Untuk menjawab pertanyaan a diperlukan distribusi frekuensi, untuk menjawab pertanyaan b diperlukan distribusi frekuensi relatif dan untuk menjawab pertanyaan c diperlukan distribusi frekuensi kumulatif. a. Tabel distribusi frekuensi untuk data tersebut ialah sebagai berikut. T abel N ilai S tatistik 50 mhs Mahasiswa FE U”X” Smt II, 1 997 Banyaknya mahasiswa yang mendapat nilai antara 44-52 adalah 2 orang dan antara 80 - 88 adalah 13 orang. Nilai Frekuensi ( f ) 35 -43 3 44-52 2 53 -61 3 62 -70 7 71 -79 13 80- 88 13 89 -97 9 Jumlah 50

36. Jenis-jenis Distribusi Frekuensi b. Tabel distribusi frekuensi relatif untuk data tersebut ialah T abel D istribusi Frekuensi Relatif Nilai S tatistik 50 mhs F EU”X” semester II, 1997 Jadi, mahasiswa yang mendapat nilai antara 53-61 adala h 6% dan yang mendapat nilai antara 89 - 97 adalah 18%. Nilai Frekuensi Frekuensi Relatif (%) 35 -43 3 6 44-52 2 4 53-61 3 6 62-70 7 14 71 -79 13 26 80-88 13 26 89 -97 9 18 Jumlah 50 100

37. Jenis-jenis Distribusi Frekuensi c . Tabel distribusi frekuensi kumulatif untuk data tersebut ialah T abel D istribusi Frekuensi kumulatif Nilai S tatistik 50 mhs F EU”X” semester II, 1997 Jadi, banyaknya mahasiswa yang nilainya kurang dari 44 adalah 3 orang dan yang kurang dari 71 adalah 15 orang. Nilai f Frekuensi Kumulatif ( f kumulatif ) Nilai f t Kurang Dari < 35 0 35 -43 3 < 44 3 44-52 2 < 53 5 53-61 3 < 62 8 62-70 7 < 71 15 71 -79 13 < 80 28 80-88 13 < 89 41 89-97 9 < 98 50

38. Jenis-jenis Distribusi Frekuensi Lati h an soal: Berikut ini adalah mid point dari pengukuran 40 diameter pipa-pipa beserta frekuensinya . S usunlah mi d po int tersebut ke dalam distribusi frekuensi biasa dan gambarkan histogram dan poligonnya! Buatlah distribusi frekuensi relatif! Buatlah distribusi frekuensi kumulatif kurang dari dan lebih dari serta gambarkan ogifnya masing-masing! Mid Point Frekuensi 66 3 69 6 72 12 75 13 78 4 81 2

39. Selesai Terimakasih