An arithmetic progression is a sequence of numbers where each term after the first is calculated by adding a fixed number, called the common difference, to the previous term. The nth term can be calculated as an = a + (n - 1)d, where a is the first term and d is the common difference. An arithmetic progression can be either finite, with a fixed number of terms, or infinite, with an unlimited number of terms. The sum of the first n terms of an arithmetic progression is given by Sn = n/2(2a + (n-1)d).

1. ARITHMETIC PROGRESSIONARITHMETIC PROGRESSION
MADE BY :-MADE BY :-
NAME :- PRANAV GHILDIYALNAME :- PRANAV GHILDIYAL
CLASS :- X DCLASS :- X D

2. What is Arithmetic ProgressionsWhat is Arithmetic Progressions
• An arithmetic progression is a list of numbers in which each term is obtained
by
adding a fixed number to the preceding term except the first term.
• This fixed number is called the common difference of the AP. Remember that it
can be positive, negative or zero.
• Each of the number in the A.P. is known as term.
• A, a+d, a+2d, a+3d with a as first term and common difference d is known as
general form of an A.P.
• There are two types of A.P. FINITE- which has only finite number of terms.
INFINITE- which has infinite number of terms.
Pattern OR A.P.
• A pattern is a type of theme of recurring events or objects, sometimes
referred to as elements of a set of objects. It is different from an A.P. as A.P.
has a common difference between two terms but pattern doesn’t have.

3. Types of progressions
Arithmetic Progression
• an arithmetic progression (AP) isan arithmetic progression (AP) is
a sequence of numbers such that thea sequence of numbers such that the
difference between the consecutivedifference between the consecutive
terms is same. For instance, theterms is same. For instance, the
sequence 3, 5, 7, 9, 11, 13, … is ansequence 3, 5, 7, 9, 11, 13, … is an
arithmetic progression with commonarithmetic progression with common
difference 2.difference 2.
• If the initial term of an arithmeticIf the initial term of an arithmetic
progression is aprogression is a11 and the commonand the common
difference of successive members is d,difference of successive members is d,
then the nth term of the sequence isthen the nth term of the sequence is
given by:given by: aann = a +(n-1)d= a +(n-1)d
• There are two types of A.P. FINITE-There are two types of A.P. FINITE-
which has only finite number of terms.which has only finite number of terms.
INFINITE- which has infinite number ofINFINITE- which has infinite number of
terms.terms.
Geometric progressionGeometric progression
• a geometric progression isa geometric progression is
a sequence of numbers where eacha sequence of numbers where each
term after the first is found byterm after the first is found by
multiplying the previous one by amultiplying the previous one by a
fixed non-zero number calledfixed non-zero number called
the common ratio. For satisfyingthe common ratio. For satisfying
G.P., three consecutive terms a ,bG.P., three consecutive terms a ,b
andand
c shall satisfy the followingc shall satisfy the following
equation: bequation: b22
= ac For example, the= ac For example, the
sequence 2, 6, 18, 54, ... is asequence 2, 6, 18, 54, ... is a
geometric progression with commongeometric progression with common
ratio 3. Similarly 10, 5, 2.5, 1.25, ... isratio 3. Similarly 10, 5, 2.5, 1.25, ... is
a geometric sequence with commona geometric sequence with common
ratio 1/2. The sum of the terms of aratio 1/2. The sum of the terms of a
geometric progression is known asgeometric progression is known as
a geometric series.a geometric series.

4. FINITE AND INFINITE A.P.FINITE AND INFINITE A.P.
Finite
• Arithmetic progressions which
have fixed number of terms is
defined as finite arithmetic
progression.
• Example:-
• 1, 3, 5, 7, c.d. = 2
• –7, –3, 1, 5, 9 c.d. = 4
• 8, 5, 2, –1, –4 c.d. = –3
• Last term is known
Infinite
• Arithmetic progressions which
have unfixed number of terms is
defined as infinite arithmetic
progression.
• Example:-
• 1,8,15,22………….. c.d = 7
• 11,22,33…………… c.d. = 11
• Last term is unknown

5. ARITHMETIC MEANARITHMETIC MEAN
• When three numbers are in A.P., the middle term is called arithmetic mean (AM) of
the two others.
• Let a and b are two numbers.
• And A be the arithmetic mean between two numbers.
• So a A b are in A.P.
• or, A – a = b – A
• or, 2A = a + b
• A =a+b/2
• So, in general
• A.M. = Sum of the numbers/2

6. FORMULAS IN THE CHAPTERFORMULAS IN THE CHAPTER
• aan = a +(n-1)dn = a +(n-1)d
• SSn =n/2[2a+(n-1)d]n =n/2[2a+(n-1)d]
OROR
• SSnn= (a+a= (a+ann))
The sum of first n positive integer isThe sum of first n positive integer is
given bygiven by
• ssnn=n(n+1)/2=n(n+1)/2

7. Derivation of aDerivation of ann
the second term a2 = a + d = a + (2 – 1) d
the third term a3 = a2 + d = (a + d) + d = a + 2d = a + (3 – 1) d
the fourth term a4 = a3 + d = (a + 2d) + d = a + 3d = a + (4 – 1) d
we can say that the nth term an = a + (n – 1) d.
So, the nth term an of the AP with first term a and common
difference d is
given by an = a + (n – 1) d.

8. Derivation of SDerivation of Snn
S = a + (a + d ) + (a + 2d) + . . . + [a + (n – 1) d ] ............................................... (1)
Rewriting the terms in reverse order, we have
S = [a + (n – 1) d] + [a + (n – 2) d ] + . . . + (a + d) + a ........................................(2)
On adding (1) and (2), term-wise. we get
2S =[2a +(n-1)d] + [2a +(n-1)d] + …….[2a +(n-1)d] + [2a +(n-1)d [n times]
or, 2S = n [2a + (n – 1) d ] (Since, there are n terms)
or, S = n/2 [2a + (n – 1) d ]
So, the sum of the first n terms of an AP is given by
S = n/2 [2a + (n – 1) d ]
i.e., S =n/2 (a + an ) ………………………………………………………………… (3)
Now, if there are only n terms in an AP, then an = l, the last term. From (3), we see that
S =n/2 (a + l )

9. Finding aFinding ann,, SSnn, n, d, a, n, d, a

10. GIVEN THATGIVEN THAT
an = a + (n − 1)d
∴ 50 = 5 + (n − 1)3
45 = (n − 1)3
15 = n − 1
n = 16

11. GIVEN THATGIVEN THAT an = a + (n − 1) d,
∴ a13 = a + (13 − 1) d
35 = 7 + 12 d
35 − 7 = 12d
28 = 12d

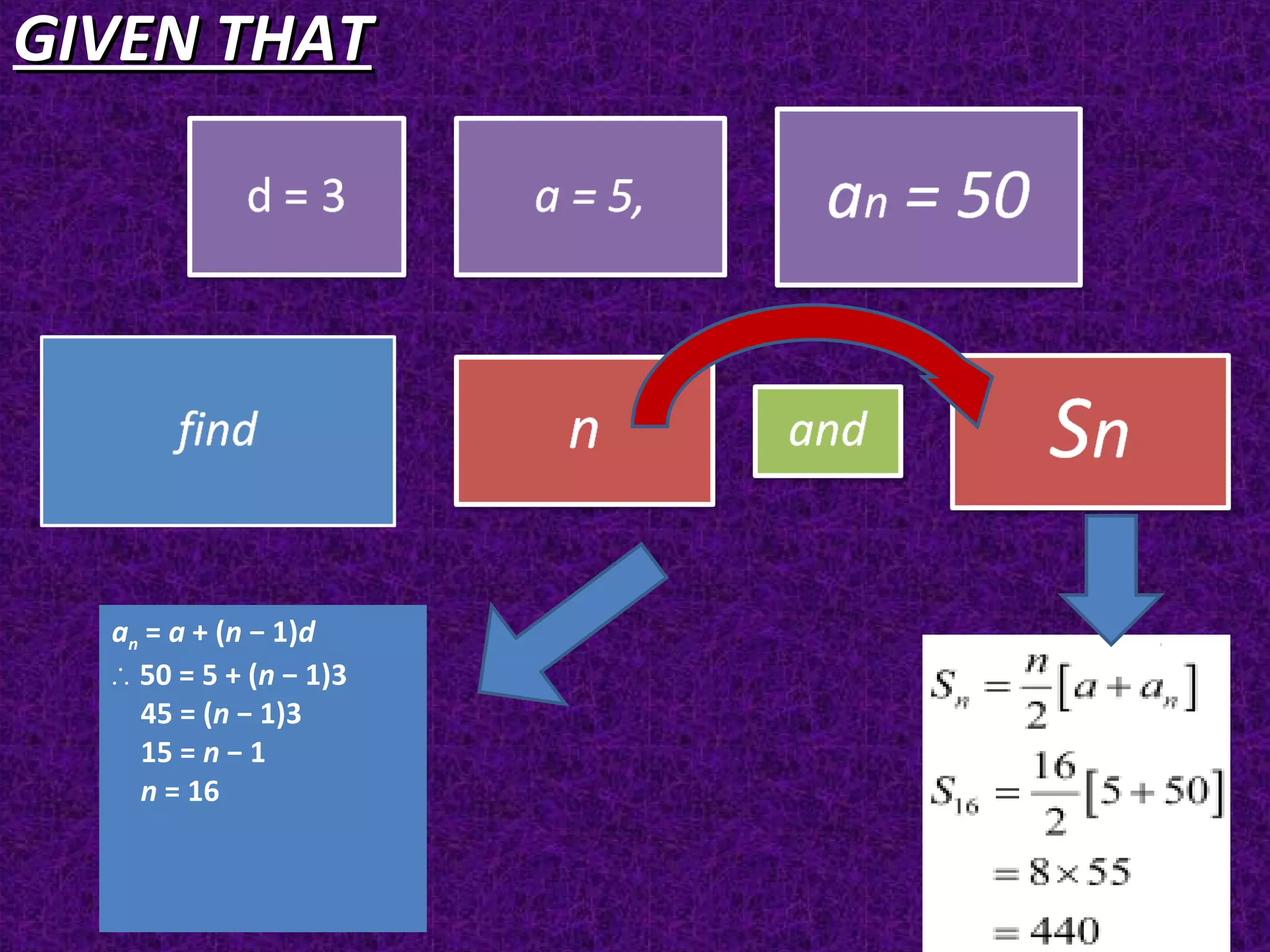
12. GIVEN THATGIVEN THAT
find n and an.
90 = n [2 + (n − 1)4]
90 = n [2 + 4n − 4]
90 = n (4n − 2) = 4n2
− 2n
4n2
− 2n − 90 = 0
4n2
− 20n + 18n − 90 = 0
4n (n − 5) + 18 (n − 5) = 0
(n − 5) (4n + 18) = 0
Either n − 5 = 0 or 4n + 18 =
0
n = 5 or
However, n can neither be
negative nor fractional.
Therefore, n = 5

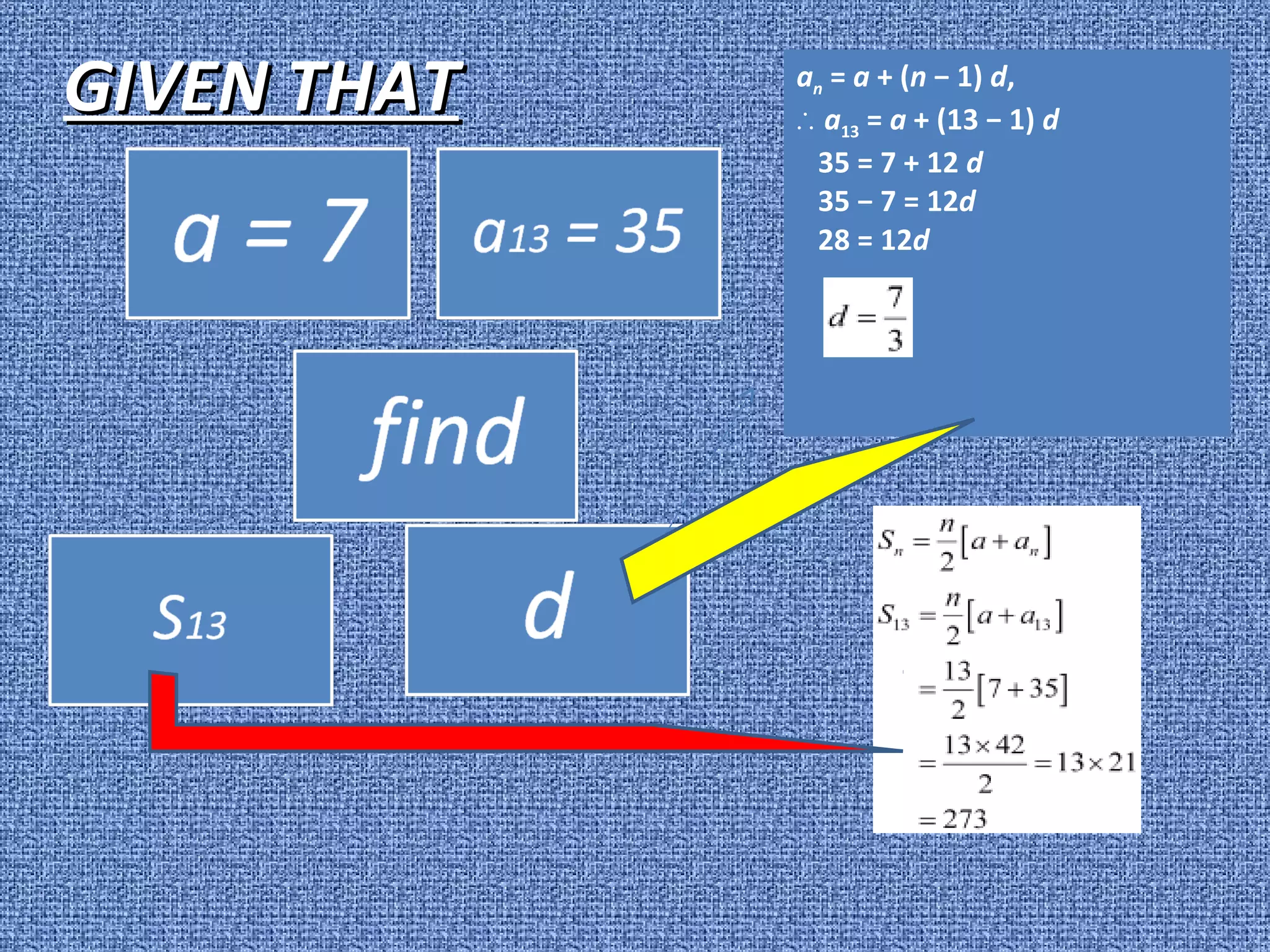
13. a = 3
n = 8
S = 192
a = 3
n = 8
S = 192
as 192 = 4 [6 + 7d]
48 = 6 + 7d
42 = 7d
d = 6
Find
d
GIVEN THAT
GIVEN THAT

14. (16) × (2) = a + 28
32 = a + 28
a = 4
GIVEN THATGIVEN THAT

15. Check whether 301 is a term of the list of numbers
5,11,17,23….
the given list of numbers is an AP. With a = 5 and d = 6.the given list of numbers is an AP. With a = 5 and d = 6.
Let 301 be a term, say, theLet 301 be a term, say, the nth term of the this AP.nth term of the this AP.
We know thatWe know that aann = a + (n – 1) d= a + (n – 1) d
So, 301 = 5 + (So, 301 = 5 + (n – 1) × 6n – 1) × 6
i.e., 301 = 6i.e., 301 = 6n – 1n – 1
So,So, n = 302/6 OR 151/3n = 302/6 OR 151/3
ButBut n should be a positive integer . So, 301 is not an should be a positive integer . So, 301 is not a
term of the given list ofterm of the given list of numbers.numbers.

16. EXAMPLES OF A.P. IN REAL LIFEEXAMPLES OF A.P. IN REAL LIFE
• Increament in salary of a preson in rupees not
in percentage
• If we take installment as increasing order or
decreasing order of rupees this also is in AP
• Days in a month..... 1,2,3,4,......
.
.
.