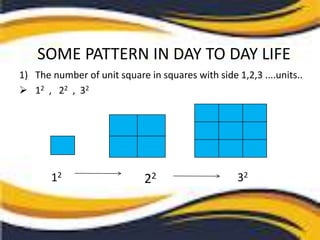
The document defines and provides examples of arithmetic progressions (AP). An AP is a sequence of numbers where each term is calculated by adding a fixed number (the common difference) to the preceding term. Examples given include the heights of students in line increasing by 1 each time, and daily temperatures decreasing by 0.1 degrees each day. Finite APs have a last term, while infinite APs do not. The general form of an AP is shown as a, a+d, a+2d, a+3d, etc., where a is the first term and d is the common difference.

1. ARITHMETIC PROGRESSIONS
GROUP 1
Members:- Akshita bansal, Sadhgi Mehta, Md. Hamiz, Payal
Aggarwal, Kainat Raza, Bhavya Mittal, Md. Zaid

2. What does the term Arithmetic
Progression mean?
 Arithmetic – Mathematical
Numbers
Progression – Moving from one
number to another

3. SOME PATTERN IN DAY TO DAY LIFE
1) The number of unit square in squares with side 1,2,3 ....units..
 12 , 22 , 32
12
22 32

4. SOME REAL LIFE EXAMPLES OF AP

5. SOME REAL LIFE EXAMPLES OF AP

6. What is a sequence?
A sequence is a set of numbers written in a
particular order.
Examples of sequence:-
 1 , 3 , 5 , 7 , 9....
 1 , 4 , 9 , 16 , 25....

7. What are Arithmetic Progressions?
An arithmetic Progressions is a sequence or list
of numbers in which each term is obtained by
adding a fixed number to the preceding term
except the first term.

8. For example:- 1) The heights of some students
of a school standing in a queue in a morning
assembly.
147, 148, 149,..., 157.
2) The minimum temperature recorded for a
week in January,
-3.1 , -3.0 , -2.9 , -2.8 , -2.7 ....

9. For example:-
1 , 2 , 3 , 4 , 5 , 6 ,.......10
So, each of the numbers in the list is called a term.
Here -1 is the fixed number which is the common difference
of the AP. This common number can either be positive,
negative or zero..
-1 -1
-1 -1 -1

10. For example:-
1 , 2 , 3 , 4 , 5 , 6 ,.......10
-1 -1
-1 -1 -1
The first term of the AP is denoted by a1 and then
second term as a2 and so on..The last term of AP is
denoted as an .
The common difference is denoted by d ..

11. General form of an AP
 The General form of an A.P is
a,a+d,a+2d,a+3d...
where ‘d’ is the common difference and ‘a’ is the first
term of AP.

12. Finite and Infinite AP
I. Finite Arithmetic Progressions :- A finite AP is
a sequence of numbers which has a last term.
Examples:-
1) 147,148,149,150,..........,157.
2) 950,900,850,800,.........,50.
3) 200,250,300,350,.........,750
And many more...

13. Finite and Infinite AP
II. Infinite Arithmetic Progressions :- A Infinite AP is
a sequence of numbers which do not have a last
term.
Examples:-
1) 1,2,3,4.....
2) 1,3,5,7....
3) 2,4,6,8......
And many more...

14. For example:-
6 , 9, 12 , 15...
For finding the common difference, we will subtract the
consecutive terms..
a1 = 6
a2 = 9
a3 = 12
a4 = 15
a2 - a1 = 9-6 = 3
a3 - a2 = 12-9 = 3
a4 - a3 = 15-12 = 3
Since, the common difference between the
consecutive terms is same..Hence, it is an
Arithmetic Progression (AP)...