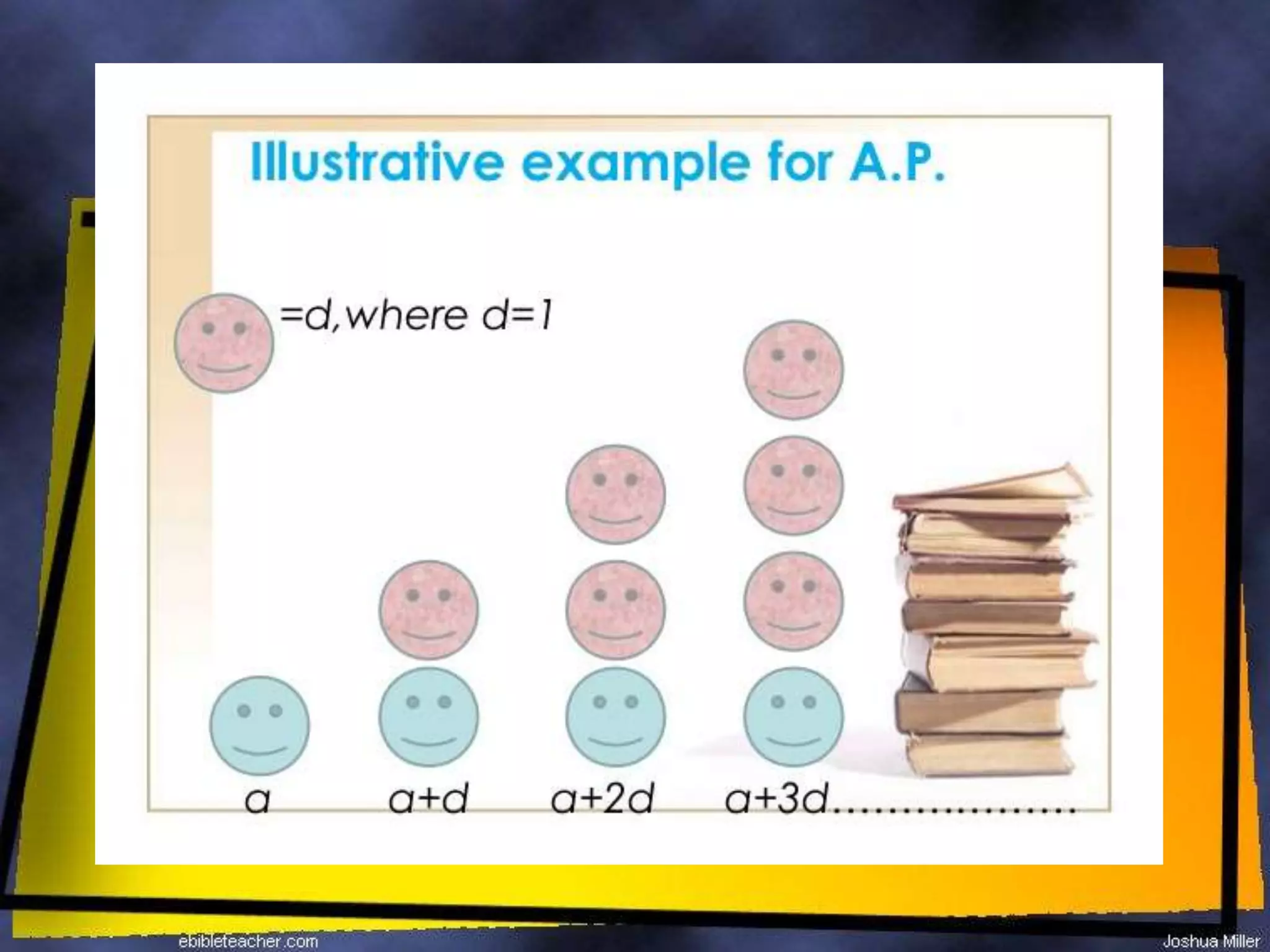
An arithmetic progression (AP) is a sequence where the difference between consecutive terms is constant, exemplified by sequences like 2, 4, 6, 8 and 5, 10, 15, 20. The nth term of an AP can be calculated using the formula an = a + (n-1)d, where 'a' is the first term and 'd' is the common difference. The sum of the first n terms of an AP is given by the formula Sn = n/2(2a + (n-1)d).

1. Arithmetic Progression

2.  Arithmetic Sequence is a sequence of
numbers such that the difference between
the consecutive terms is constant.
 For instance, the sequence 5, 7, 9, 11, 13,
15 … is an arithmetic progression with
common difference of 2. &
 2,6,18,54(next term to the term is to
be obtained by multiplying by 3.
Arithmetic Sequence

4. Arithmetic Progression
If various terms of a sequence are formed by adding a
fixed number to the previous term or the difference
between two successive terms is a fixed number, then the
sequence is called AP.
e.g.1) 2, 4, 6, 8, ……… the sequence of even numbers is
an example of AP
 2) 5, 10, 15, 20, 25….. In this each term is obtained by
adding 5 to the preceding term except first term.

5.  If the initial term of an arithmetic progression is a1
and the common difference of successive members
is d, then the nth term of the sequence (an) is given
by:
 and in general

6. • A finite portion of an arithmetic progression is called a finite
arithmetic progression and sometimes just called an arithmetic
progression. The sum of a finite arithmetic progression is called
an Arithmetic series.
• The behavior of the arithmetic progression depends on the
common difference d. If the common difference is:
 Positive, the members (terms) will grow towards positive infinity.
 Negative, the members (terms) will grow towards negative
infinity.

7. Common Difference




If we take first term of an AP as a and Common Difference as d. Then-nth term of that AP will be An = a + (n-1)d.
For instance--- 3, 7, 11, 15, 19 … d =4 a =3
Notice in this sequence that if we find the difference between any term
and the term before it we always get 4.
 4 is then called the common difference and is denoted with the letter
d.
 To get to the next term in the sequence we would add 4 so a recursive
formula for this sequence is:
an  an1  4
 The first term in the sequence would be a1 which is sometimes just
written as a.

8. Example
Let a=2, d=2, n=12,find An
An=a+(n-1)d
=2+(12-1)2
=2+(11)2
=2+22
Therefore, An=24
Hence solved.

9. The difference between two terms of
an AP
The difference between two terms of
an AP can be formulated as below:nth term – kth term
= t(n) – t(k)
= {a + (n-1)d} – { a + (k-1) d }
= a + nd – d – a – kd + d = nd – kd
Hence,
t(n) – t(k) = (n – k) d

10. General Formulas of AP
• The general forms of an AP is a,(a+d), (a+2d),. .. , a +
( m - 1)d.
i. Nth term of the AP is Tn =a+(n-1)d.
ii. Nth term form the end ={l-(n-1)d}, where l is the
last term of the word.
iii. Sum of 1st n term of an AP is Sn=N/2{2a=(n-1)d}.
iv. Also Sn=n/2 (a+1)
v. Tn =(sn-Sn-1)

11. The sum of n terms, we find as,
Sum = n X [(first term + last term) / 2]
Now last term will be = a + (n-1) d
Therefore,
Sum(Sn) =n X [{a + a + (n-1) d } /2 ]
= n/2 [ 2a + (n+1)d]

12. • Solution.
10)
n - 1 = 80
11)
n = 80 + 1
1)
First term is a = 100 , an = 500
2)
Common difference is d = 105 12)
100 = 5
3)
nth term is an = a + (n-1)d
4)
500 = 100 + (n-1)5
5)
500 - 100 = 5(n – 1)
6)
400 = 5(n – 1)
7)
5(n – 1) = 400
8)
5(n – 1) = 400
9)
n – 1 = 400/5

n = 81
Hence the no. of terms are 81.