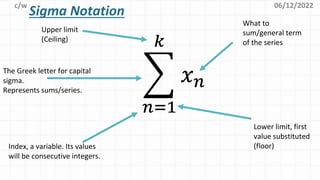
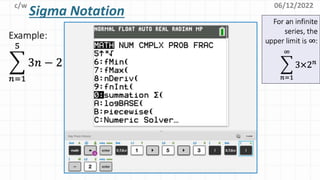
This document provides an introduction to using sigma notation for summation. It defines key terms like sequence, series, and sigma notation. Examples are given to show how to write out sigma notation for different sums. There is also a section on quick practice problems for students to work through. The objectives are for students to be able to recognize sigma notation and apply it to find sums of sequences.

1. 06/12/2022
c/w
▪ Introduction to the
use of sigma
notation for
summation
Learning Objectives:
Students will be able to recognize the concept of
sigma notation.
Apply the concept of sigma notation in finding
sum of sequence.

2. Sequence versus Series
Sequence: list of number in a specific order
Series: sum of the list (or sequence).
06/12/2022
c/w
3, 7, 11, 15, …
3 + 7 + 11 + 15 + …

3. Sigma Notation
06/12/2022
c/w
What to
sum/general term
of the series
Upper limit
(Ceiling)
Index, a variable. Its values
will be consecutive integers.
Lower limit, first
value substituted
(floor)
The Greek letter for capital
sigma.
Represents sums/series.

4. Sigma Notation
06/12/2022
c/w

5. Sigma Notation – More Examples
06/12/2022
c/w

6. Sigma Notation
06/12/2022
c/w

7. Quick Practice
06/12/2022
c/w

8. Quick Practice
06/12/2022
c/w

9. Discussion
06/12/2022
c/w

10. Finite sum of arithmetic series
14/12/2021
Activity

11. Finite sum of arithmetic series
▪
14/12/2021
c/w

12. Finite sum of arithmetic series
14/12/2021
c/w

13. 14/12/2021
c/w

14. Solve in a paper – upload at the end of the
lesson
14/12/2021
c/w

15. Check your understanding 14/12/2021
c/w
The first term of an arithmetic series is a and the common difference is d.
The 18th term of the series is 25 and the 21st term of the series is
(a) Use this information to write down two equations for a and d.
(2)
(b) Show that a = –7.5 and find the value of d.
(2)
The sum of the first n terms of the series is 2750.
(c) Show that n is given by
(4)
(d) Hence find the value of n.
(3)
(Total 11 marks)

16. Check your understanding
14/12/2021
c/w
A particular list of N consecutive integers starts with 1111 as follows:
1111, 1112, 1113, … , 1111 + N − 1
The entire list is shifted D places along the number line and the first number
then excluded, leaving a list of N−1 larger consecutive numbers as follows:
1112 + D, 1113 + D, …, 1111 + N − 1 +D
In each list the sum of the integers is the same.
What are the possibilities for N and D?

17. Plenary
14/12/2021
c/w
Does mathematics always reflect reality?
Are fractals invented or discovered?

18. 14/12/2021
c/w
▪ Apply geometric and
arithmetic sequences in
real life situations
Application of Sequences

19. Simple Interest
▪
14/12/2021
c/w
I – interest
PV – Present value
FV = Future value
n – total years
r – interest rate

20. Compound Interest
▪
14/12/2021
c/w
Durations k Value
Yearly/annum/
annually/p.a
k = 1
Half yearly k = 2
Quarterly k = 4
Monthly k = 12
Future value
present value
Interest rate
Number of
compounding
periods per year
Total
years

21. Simple Interest and Compound Interest
$1000 is invested into an account
that pays 5% per annum on simple
interest 4 years.
14/12/2021
c/w
$1000 is invested into an account that pays
5% per annum compound interest. Interest is
compounded monthly for 4 years.

22. Compound and Simple Interest
Sebastian took out a $35000
loan for a new car. The bank
offered him 2.5% p.a simple
interest for 5 years. Calculate
the total value Sebastian has
to repay the bank.
14/12/2021
c/w
Habib put $5000 into savings
account that pays 4% interest
p.a, compounded monthly.
How much will be in the
account after 4 years if Habib
does not deposit or withdraw
any money?
Leslie got a student loan of
$12090 CAD. If Leslie has to
repay $16000 CAD in 2
years, what is the annual
interest rate if the interest
on the loan is compounded
monthly?

23. Compound Interest
Oliver’s savings account now has a balance of $900. If the interest rate was
1.5% per annum, compounded quarterly, how much did Oliver originally
deposit six years ago if her has not withdrawn or deposited any money since?
14/12/2021
c/w

24. Check your understanding
14/12/2021
c/w
SL - Page 39 Question 1
SL - Page 39 Question 5
SL - Page 40 Question 2
SL - Page 40 Question 7 and 8

25. Button timers - cream
En
d
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
En
d
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
En
d
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
En
d
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
En
d
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
En
d
1
2
3
4
5
6
7
8
9
10

26. 5 minute full circle timers
5 minutes 5 minutes 5 minutes

27. 14/12/2021
c/w
Think – Pair – Share
Discuss in pairs