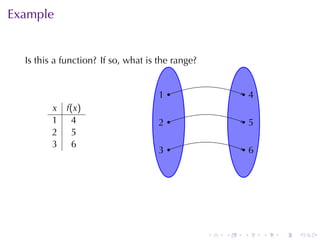
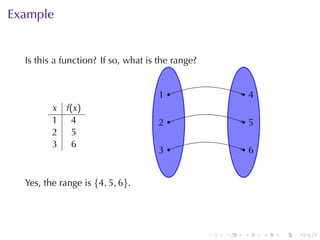
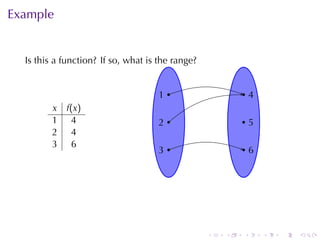
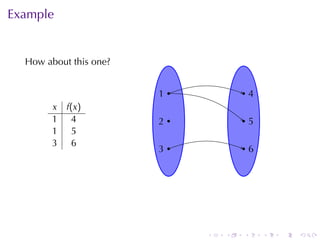
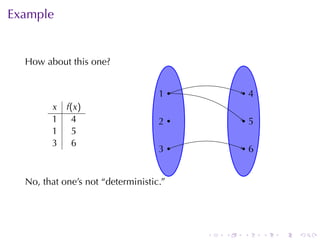
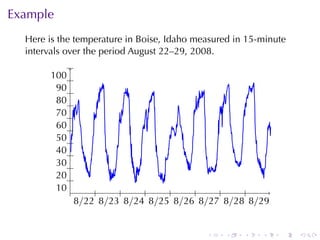
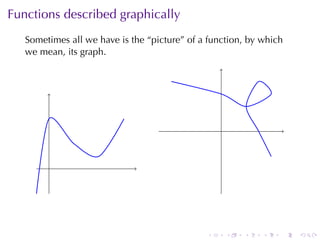
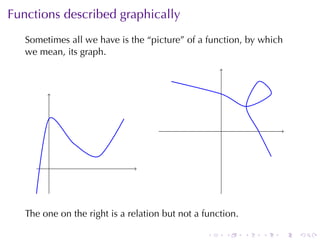
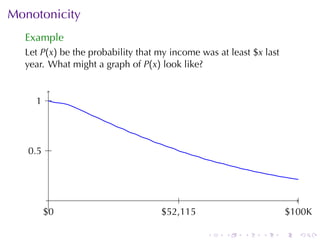
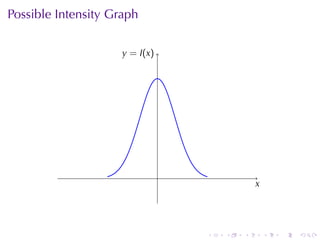
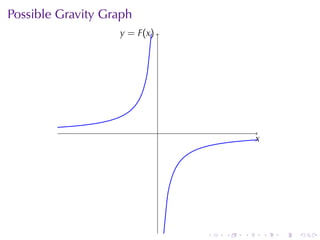
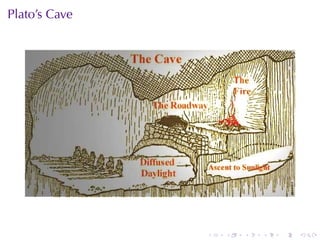
The document provides an overview of functions including definitions, examples, and properties. It defines a function as a relation that assigns each element in the domain to a single element in the range. Examples of functions expressed by formulas, numerically, graphically, and verbally are given. Properties like monotonicity, symmetry, evenness, and oddness are defined and illustrated with examples. The document aims to introduce the fundamental concepts of functions to readers.

1. Section 1.1
Functions
V63.0121.006/016, Calculus I
January 19, 2010
Announcements
Syllabus is on the common Blackboard
Office Hours TBA
. . . . . .

2. Outline
What is a function?
Modeling
Examples of functions
Functions expressed by formulas
Functions described numerically
Functions described graphically
Functions described verbally
Properties of functions
Monotonicity
Symmetry
. . . . . .

3. Definition
A function f is a relation which assigns to to every element x in a
set D a single element f(x) in a set E.
The set D is called the domain of f.
The set E is called the target of f.
The set { f(x) | x ∈ D } is called the range of f.
. . . . . .

4. Outline
What is a function?
Modeling
Examples of functions
Functions expressed by formulas
Functions described numerically
Functions described graphically
Functions described verbally
Properties of functions
Monotonicity
Symmetry
. . . . . .

5. The Modeling Process
. .
Real-world
.
. m
. odel Mathematical
.
Problems Model
s
. olve
.est
t
. i
.nterpret .
Real-world
. Mathematical
.
Predictions Conclusions
. . . . . .

6. Plato’s Cave
. . . . . .

7. The Modeling Process
. .
Real-world
.
. m
. odel Mathematical
.
Problems Model
s
. olve
.est
t
. i
.nterpret .
Real-world
. Mathematical
.
Predictions Conclusions
S
. hadows F
. orms
. . . . . .

8. Outline
What is a function?
Modeling
Examples of functions
Functions expressed by formulas
Functions described numerically
Functions described graphically
Functions described verbally
Properties of functions
Monotonicity
Symmetry
. . . . . .

9. Functions expressed by formulas
Any expression in a single variable x defines a function. In this
case, the domain is understood to be the largest set of x which
after substitution, give a real number.
. . . . . .

10. Example
x+1
Let f(x) = . Find the domain and range of f.
x−1
. . . . . .

11. Example
x+1
Let f(x) = . Find the domain and range of f.
x−1
Solution
The denominator is zero when x = 1, so the domain is all real
numbers excepting one. As for the range, we can solve
x+1 y+1
y= =⇒ x =
x−1 y−1
So as long as y ̸= 1, there is an x associated to y.
. . . . . .

12. No-no’s for expressions
Cannot have zero in the denominator of an expression
Cannot have a negative number under an even root (e.g.,
square root)
Cannot have the logarithm of a negative number
. . . . . .

13. Piecewise-defined functions
Example
Let {
x2 0 ≤ x ≤ 1;
f(x) =
3−x 1 < x ≤ 2.
Find the domain and range of f and graph the function.
. . . . . .

14. Piecewise-defined functions
Example
Let {
x2 0 ≤ x ≤ 1;
f(x) =
3−x 1 < x ≤ 2.
Find the domain and range of f and graph the function.
Solution
The domain is [0, 2]. The range is [0, 2). The graph is piecewise.
. .
2 .
. .
1 . .
. . .
0
. 1
. 2
.
. . . . . .

15. Functions described numerically
We can just describe a function by a table of values, or a diagram.
. . . . . .

16. Example
Is this a function? If so, what is the range?
x f(x)
1 4
2 5
3 6
. . . . . .

17. Example
Is this a function? If so, what is the range?
. .
1 ..
4
x f(x)
1 4 . ..
2 .. .
5
2 5
3 6
. .
3 ..
6
. . . . . .

18. Example
Is this a function? If so, what is the range?
. .
1 ..
4
x f(x)
1 4 . ..
2 .. .
5
2 5
3 6
. .
3 ..
6
Yes, the range is {4, 5, 6}.
. . . . . .

19. Example
Is this a function? If so, what is the range?
x f(x)
1 4
2 4
3 6
. . . . . .

20. Example
Is this a function? If so, what is the range?
. .
1 ..
4
x f(x)
1 4 . ..
2 .. .
5
2 4
3 6
. .
3 ..
6
. . . . . .

21. Example
Is this a function? If so, what is the range?
. .
1 ..
4
x f(x)
1 4 . ..
2 .. .
5
2 4
3 6
. .
3 ..
6
Yes, the range is {4, 6}.
. . . . . .

22. Example
How about this one?
x f(x)
1 4
1 5
3 6
. . . . . .

23. Example
How about this one?
. .
1 ..
4
x f(x)
1 4 . ..
2 .. .
5
1 5
3 6
. .
3 ..
6
. . . . . .

24. Example
How about this one?
. .
1 ..
4
x f(x)
1 4 . ..
2 .. .
5
1 5
3 6
. .
3 ..
6
No, that one’s not “deterministic.”
. . . . . .

25. In science, functions are often defined by data. Or, we observe
data and assume that it’s close to some nice continuous function.
. . . . . .

26. Example
Here is the temperature in Boise, Idaho measured in 15-minute
intervals over the period August 22–29, 2008.
.
1
. 00 .
9
.0.
8
.0.
7
.0.
6
.0.
5
.0.
4
.0.
3
.0.
2
.0.
1
.0. . . . . . . .
8
. /22 . /23 . /24 . /25 . /26 . /27 . /28 . /29
8 8 8 8 8 8 8
. . . . . .

27. Functions described graphically
Sometimes all we have is the “picture” of a function, by which
we mean, its graph.
.
.
. . . . . .

28. Functions described graphically
Sometimes all we have is the “picture” of a function, by which
we mean, its graph.
.
.
The one on the right is a relation but not a function.
. . . . . .

29. Functions described verbally
Oftentimes our functions come out of nature and have verbal
descriptions:
The temperature T(t) in this room at time t.
The elevation h(θ) of the point on the equator at longitude θ.
The utility u(x) I derive by consuming x burritos.
. . . . . .

30. Outline
What is a function?
Modeling
Examples of functions
Functions expressed by formulas
Functions described numerically
Functions described graphically
Functions described verbally
Properties of functions
Monotonicity
Symmetry
. . . . . .

31. Monotonicity
Example
Let P(x) be the probability that my income was at least $x last
year. What might a graph of P(x) look like?
. . . . . .

32. Monotonicity
Example
Let P(x) be the probability that my income was at least $x last
year. What might a graph of P(x) look like?
. .
1
. .5 .
0
. . .
$
.0 $
. 52,115 $
. 100K
. . . . . .

33. Monotonicity
Definition
A function f is decreasing if f(x1 ) > f(x2 ) whenever x1 < x2
for any two points x1 and x2 in the domain of f.
A function f is increasing if f(x1 ) < f(x2 ) whenever x1 < x2
for any two points x1 and x2 in the domain of f.
. . . . . .

34. Examples
Example
Going back to the burrito function, would you call it increasing?
. . . . . .

35. Examples
Example
Going back to the burrito function, would you call it increasing?
Example
Obviously, the temperature in Boise is neither increasing nor
decreasing.
. . . . . .

36. Symmetry
Example
Let I(x) be the intensity of light x distance from a point.
Example
Let F(x) be the gravitational force at a point x distance from a
black hole.
. . . . . .

37. Possible Intensity Graph
y
. = I(x)
.
x
.
. . . . . .

38. Possible Gravity Graph
y
. = F(x)
.
x
.
. . . . . .

39. Definitions
Definition
A function f is called even if f(−x) = f(x) for all x in the
domain of f.
A function f is called odd if f(−x) = −f(x) for all x in the
domain of f.
. . . . . .

40. Examples
Even: constants, even powers, cosine
Odd: odd powers, sine, tangent
Neither: exp, log
. . . . . .