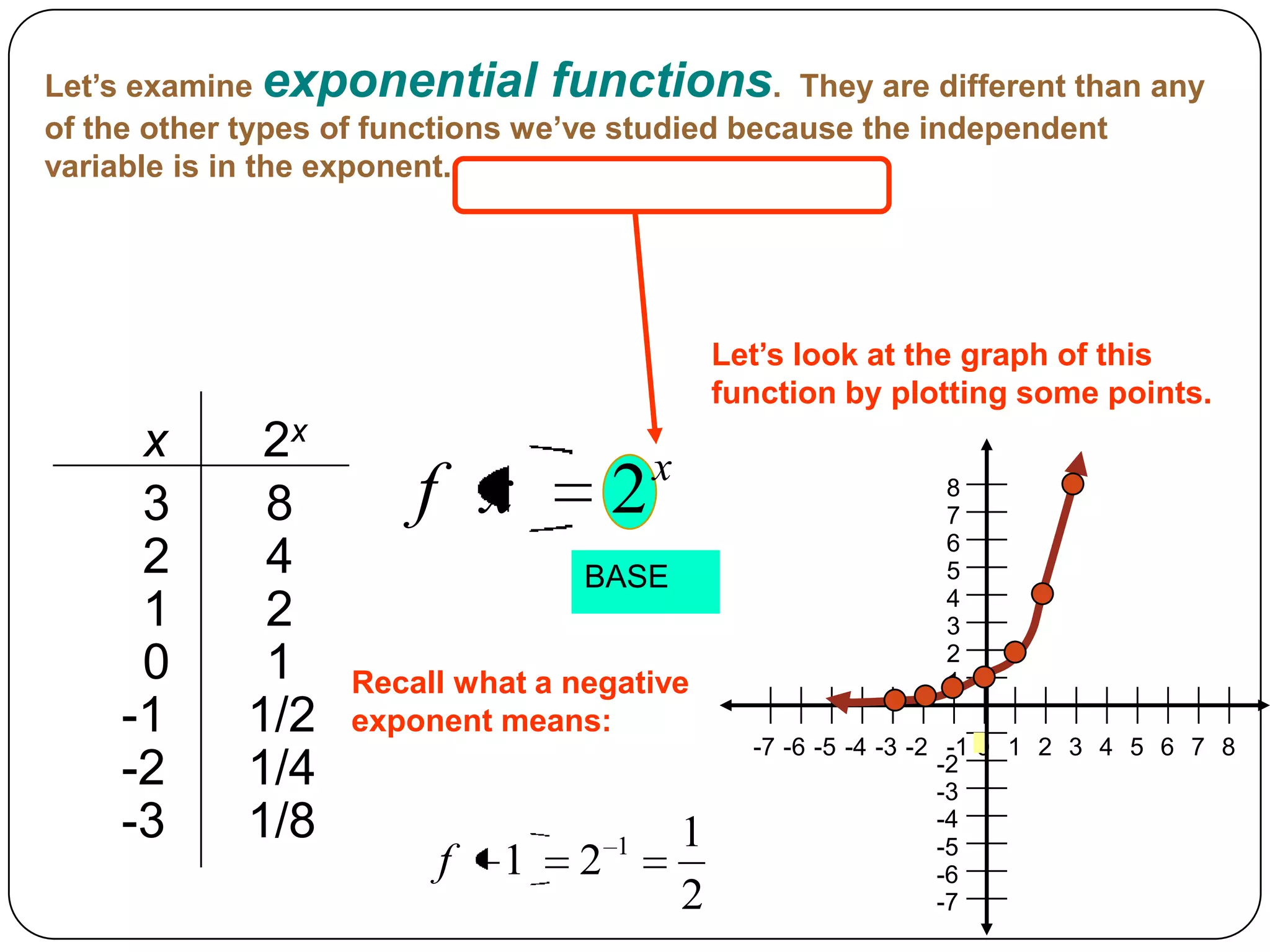
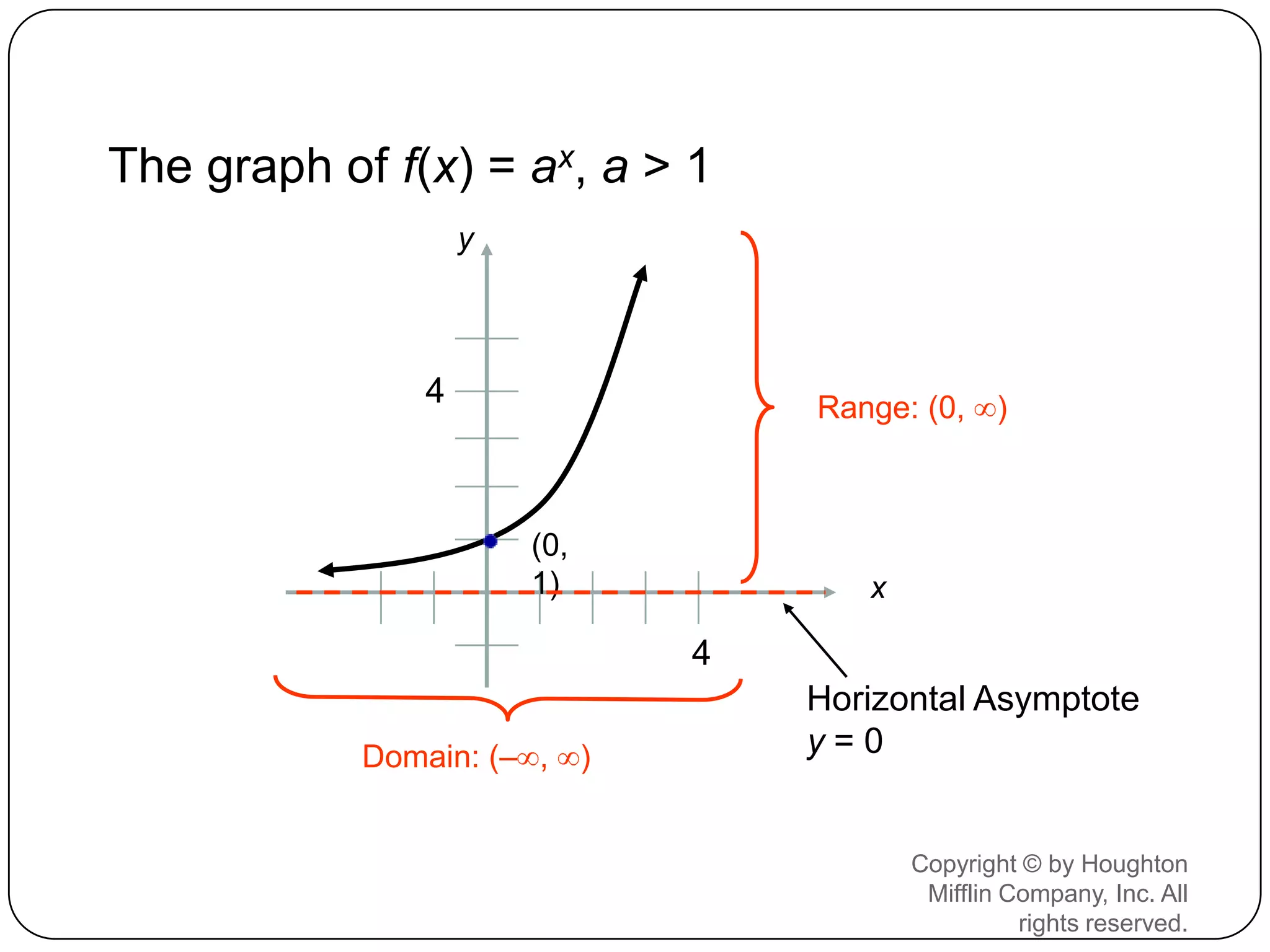
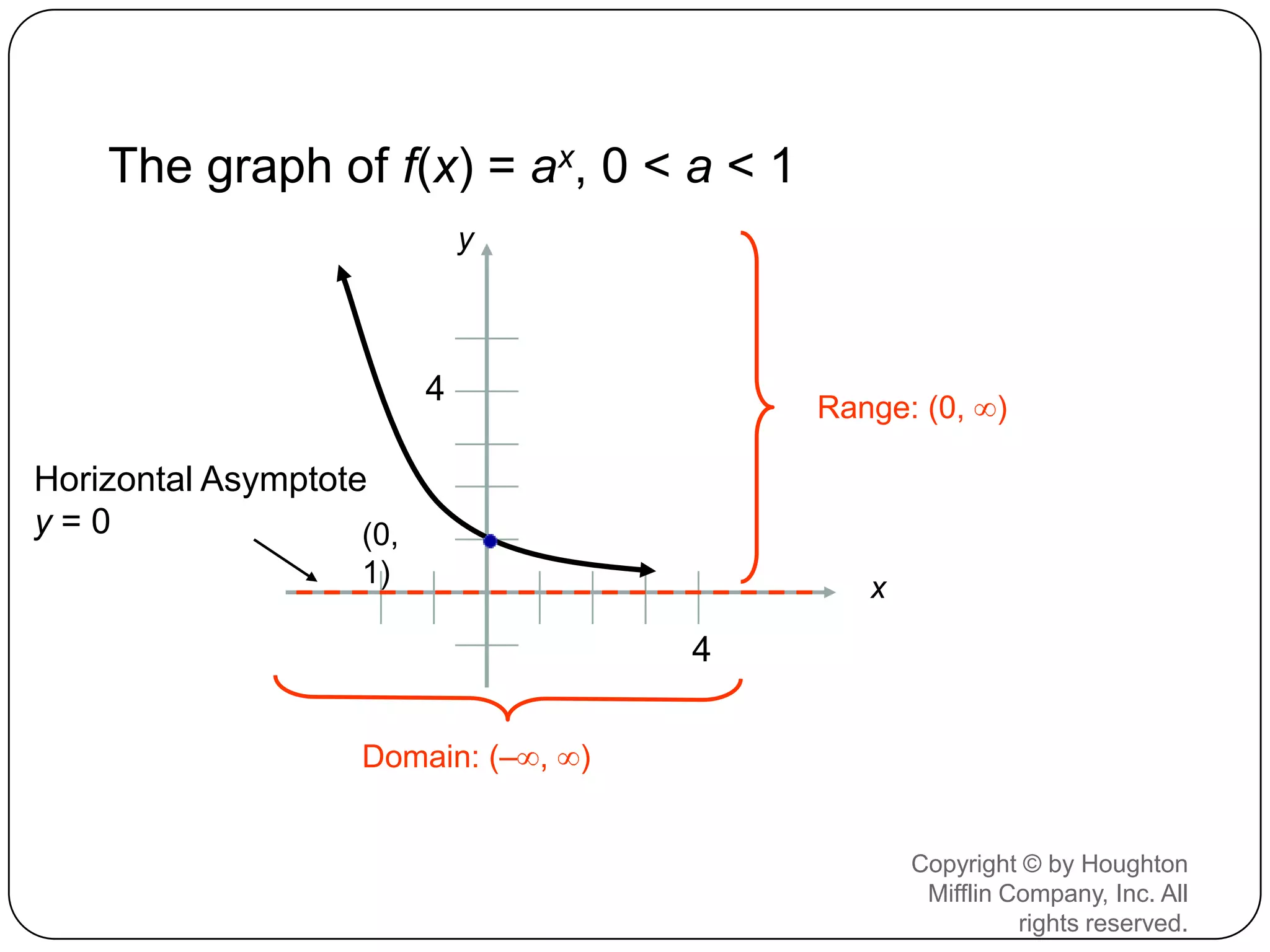
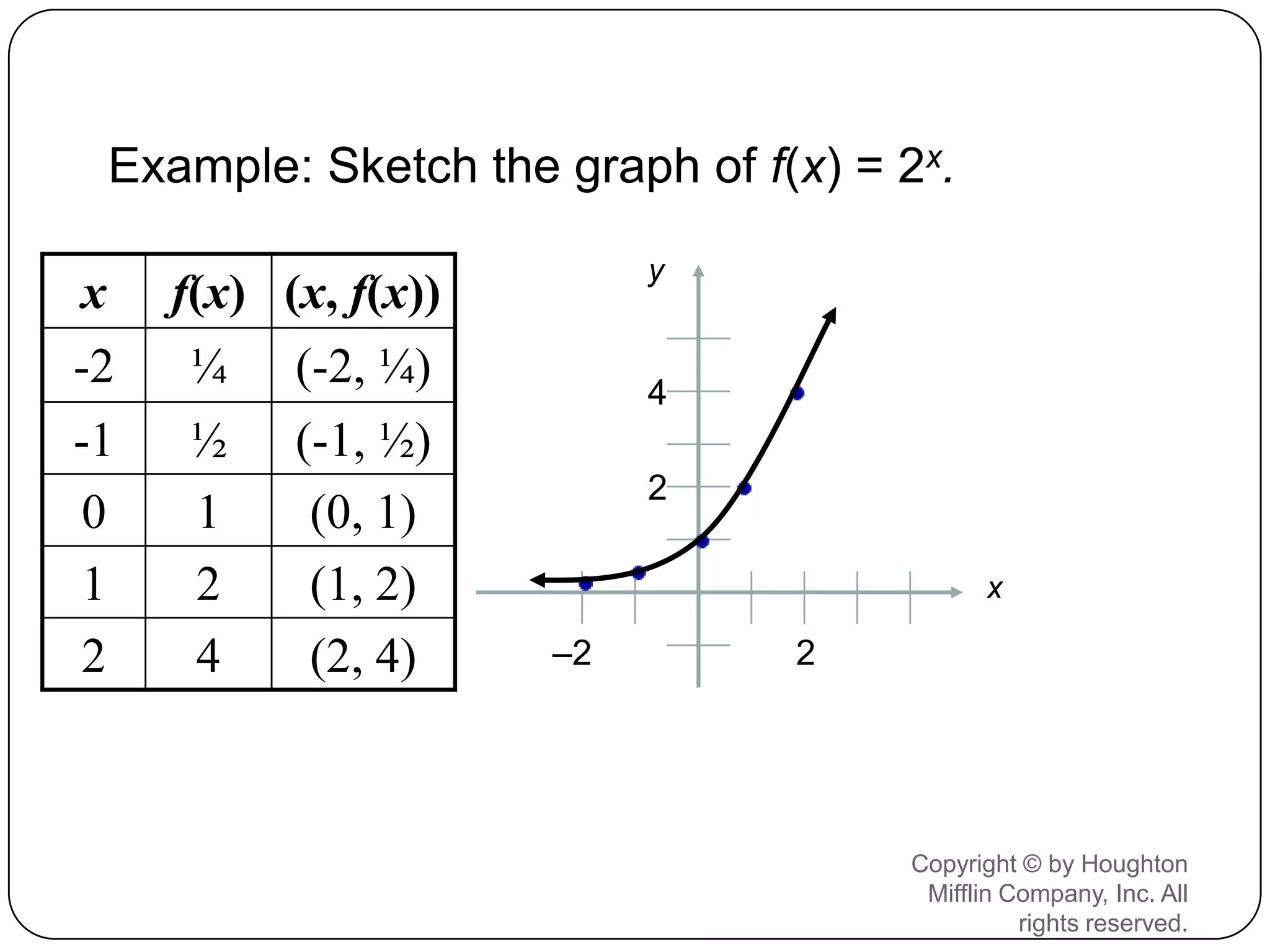
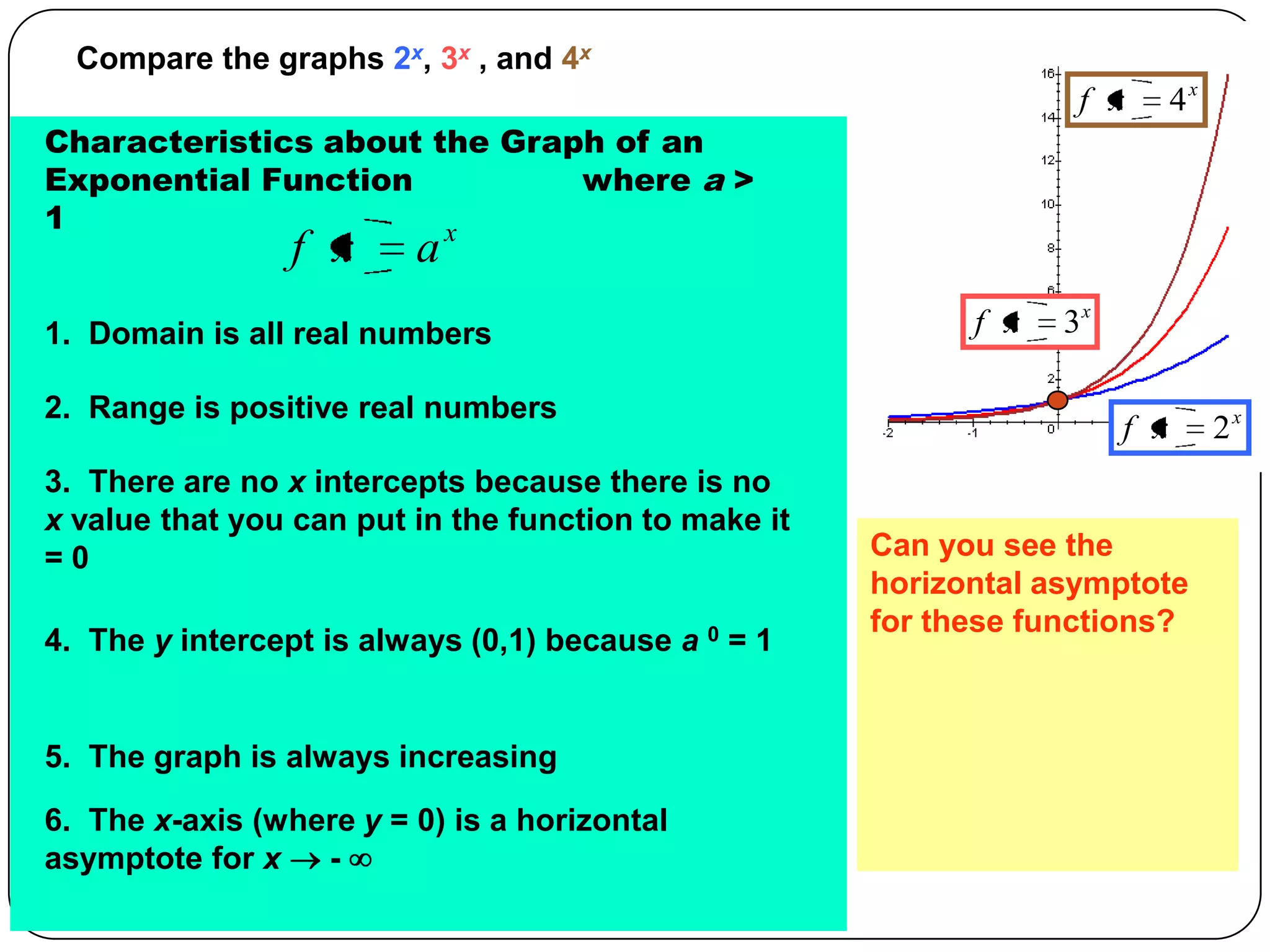
This document discusses exponents and exponential functions. It defines what exponents are, how they are read, and some of their key properties like the product rule for exponents. It also examines exponential functions where the base is raised to the power of x. The graphs of exponential functions where the base is greater than 1, between 0 and 1, and equal to 1 are explored. The graphs are always increasing, have a horizontal asymptote at y=0, and a y-intercept of (0,1). Exponential equations are also briefly covered.

1. Exponents
by
Maluleke Matimba Elliot

2. Introduction
 Exponents represent repeated multiplication. For
example,

3. Introduction
 More generally, for any non-zero real number a and
for any whole number n,
In the exponential expression an, a is called the
base and n is called the exponent.

4. Exponents Are Often Used in
Area Problems to Show the
Feet Are Squared
Length x width = area 15ft
A pool is a rectangle .
Length = 30 ft. 30ft
Width = 15 ft.
2
Area = 30 x 15 = 450
ft.

5. Exponents Are Often Used in
Volume Problems to Show the
Centimeters Are Cubed
Length x width x height =
volume
A box is a rectangle 10
Length = 10 cm. 10
Width = 10 cm. 10
Height = 20 cm.
3
Volume =

6.  a2 is read as ‘a squared’.
 a3 is read as ‘a cubed’.
 a4 is read as ‘a to the fourth power’.
...
 an is read as ‘a to the nth power’.

7. Location of Exponent
 An exponent is a little number high
and to the right of a regular or
base number.
4 Exponent
Base 3

8. Definition of Exponent
 An exponent tells how many
times a number is multiplied by
itself.
4 Exponent
Base 3

9. Some Definitions of Exponents

10. How to read an Exponent
 This exponent is read three to
the fourth power.
4 Exponent
Base 3

11. Properties of Exponents

12. Example:

13. Properties of Exponents
Homework.

14. Example:

15. Ex: All of the properties of rational exponents apply to
real exponents as well. Lucky you!
Simplify:
2 3 2 3
5 5 5
Recall the product of powers property,
am an = am+n

16. Exponential Functions
and Their Graphs

17. The exponential function f with base a is
defined by
f(x) = ax
where a > 0, a 1, and x is any real
number.
For instance,
f(x) = 3x and g(x) = 0.5x
are exponential functions.
Copyright © by Houghton
Mifflin Company, Inc. All
rights reserved.

18. Let’s examine exponential functions. They are different than any
of the other types of functions we’ve studied because the independent
variable is in the exponent.
Let’s look at the graph of this
function by plotting some points.
x 2x x
3 8 f x 2 8
7
6
2 4 BASE 5
4
1 2 3
0 1 Recall what a negative
2
1
-1 1/2 exponent means:
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
-2 1/4 -2
-3
-3 1/8 1 1 -4
-5
f 1 2 -6
2 -7

19. The value of f(x) = 3x when x = 2 is
f(2) = 32 9
=
The value of f(x) = 3x when x = –2 is
1
f(–2) = 3–2
9
=
The value of g(x) = 0.5x when x = 4 is
g(4) = 0.54 0.062
= 5
Copyright © by Houghton
Mifflin Company, Inc. All
rights reserved.

20. The graph of f(x) = ax, a > 1
y
4 Range: (0, )
(0,
1) x
4
Horizontal Asymptote
Domain: (– , ) y=0
Copyright © by Houghton
Mifflin Company, Inc. All
rights reserved.

21. The graph of f(x) = ax, 0 < a < 1
y
4
Range: (0, )
Horizontal Asymptote
y=0 (0,
1) x
4
Domain: (– , )
Copyright © by Houghton
Mifflin Company, Inc. All
rights reserved.

22. Example: Sketch the graph of f(x) = 2x.
y
x f(x) (x, f(x))
-2 ¼ (-2, ¼) 4
-1 ½ (-1, ½)
2
0 1 (0, 1)
1 2 (1, 2) x
2 4 (2, 4) –2 2
Copyright © by Houghton
Mifflin Company, Inc. All
rights reserved.

23. Compare the graphs 2x, 3x , and 4x
f x 4x
Characteristics about the Graph of an
Exponential Function where a >
1 x
f x a
1. Domain is all real numbers f x 3x
2. Range is positive real numbers
f x 2x
3. There are no x intercepts because there is no
x value that you can put in the function to make it
=0 Can these exponential
What is the range of of
Are you they intercept
What is the xthe
What is see domain an
intercept
horizontalincreasing
of these exponential or
exponential function?
functions asymptote
an exponential
of these exponential
for these functions?
functions?
function?
decreasing?
functions?
4. The y intercept is always (0,1) because a 0 = 1
5. The graph is always increasing
6. The x-axis (where y = 0) is a horizontal
asymptote for x -

24. Exponential Equations
 Let a ∈ R – {–1, 0, 1}
(a is a real number other than –1, 0 and
1).
If am = an then m = n.

25. Examples:
 2x = 16
 3x+1 = 81
 22x + 1 = 8x – 1

26. Exercises:

27. References:
Damirdag, M. (2011, 07 23). Power of Real numbers. Retrieved 03 20, 2013, from
Slideshare: http://www.slideshare.net/mstfdemirdag/exponents-8693171
Garcia, J. (2010, July 01). Exponential Functions. Retrieved March 15, 2013, from
slideshare: http://www.slideshare.net/jessicagarcia62/exponential-functions-4772163
Gautani, V. L. (2012, October 28). Multiplication properties of exponents. Retrieved
March 17, 2013, from slideshare: http://www.slideshare.net/sirgautani/multiplication-
properties-of-exponents-14917484
Joshi, N. (2011, 04 01). Laws of Exponents. Retrieved 03 15, 2013, from Slideshare:
http://www.slideshare.net/entranceisolutions/laws-of-exponents-7479833
Yuskaits, M. (2008, 06 05). Exponents. Retrieved 03 17, 2013, from slideshare:
http://www.slideshare.net/hiratufail/exponents1