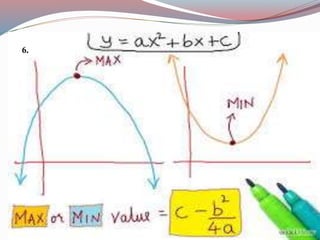
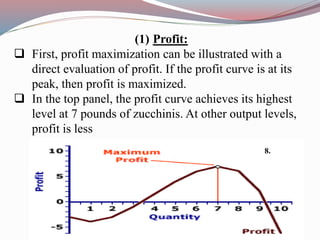
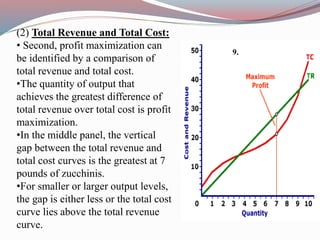
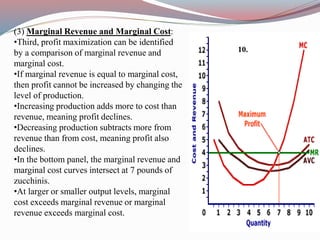
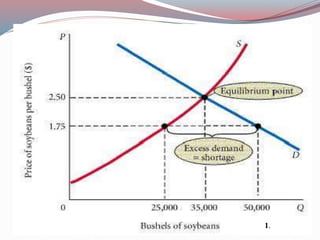
This document defines key concepts in business mathematics including derivatives, differentiation formulas, composite functions, implicit differentiation, marginal revenue, price elasticity, income elasticity, elasticity of supply, market equilibrium, cost minimization, and profit maximization. It provides formulas and explanations for each concept. Profit maximization is discussed as occurring at the level of output where marginal revenue equals marginal cost, where the difference between total revenue and total cost is highest, or at the peak of the profit curve. Cost minimization strategies include eliminating waste, simplifying processes, and negotiating better supplier prices.

1.  LIMIT & DIFFERENTIATION
 Course: BBA
 Subject: Business Mathematics
 Unit-3

2. Definition of Derivative:
 Let f(x) be a function of the variable x.
 The value of f(x) at x = a is f(a).
 When x = a+h, the value of the function f is f(a+h) so (a +
h) – f (a) is the change in the value of the function f, when
the value of x changes from ‘a’ to ‘a+h’.
 Shows the relative changes in the value of the function f,
when the value of a is increased by ‘h’.
(a h) f(a)f
h
 

3.  If the limit of (l) exists, when h → 0, it is called the
derivative of the function f(x) at x = a and it is denoted by
f’(a).
 Therefore,
 For any x in the domain of f,
0
( ) ( )
'( ) lim
h
f a h f a
f a
h
 

0
( ) ( )
'(x) lim
h
f x h f x
f
h
 


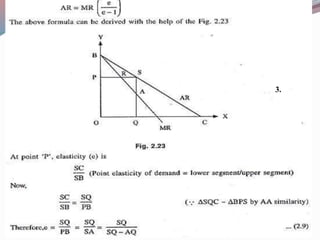
4.  f’(x) is called the derivative of f(x) with respect to x.
 If y= f (x), then the derivative of f is also denoted by dy /
dx or d / dx [f (x)].

5. Formulae for Differentiation:
 If y = c, where c is a constant, dy / dx = 0.
 If y = xn, where n is rational no. dy / dx = n x n-1
 If y = ex, then dy / dx = ex
 if y = ax, where a > 0, then dy/dx = ax logea
 If y = logex, then dy/dx = 1/x.

6. Composite function
 A composite function is a function that is composed of
two other functions. For the two functions f and g, the
composite function or the composition of f and g, is
defined by

7. • The function g(x) is substituted for x into the
function f(x).
• For example, the function F(x)=(2x+6)4 could
be considered as a composition of the
functions, f(x)=x4 and g(x)=2x+6.
• However, it could also be written as a
composition of f(x)=(2x)4 and g(x)=x+3.
Often, a function can be written as a
composition of several different combinations
of functions.

8. Implicit Differentiation
 A function whose value can only be computed indirectly fr
om one or more of the independent variables.
 For example, in the equationx2 + y2 = 1, y is an implicit fu
nction of x.

9. Applications of derivative in economic theory
Today's sophisticated international markets have helped
foster the rapid growth in derivative instruments. In the
hands of knowledgeable investors, derivatives can derive
profit from:
Changes in interest rates and equity markets around the
world
 Currency exchange rate shifts
 Changes in global supply and demand for commodities
such as agricultural products, precious and industrial
metals, and energy products such as oil and natural gas

10.  The two most widely recognized benefits attributed to
derivative instruments are price discovery and risk
management.
 They Improve Market Efficiency for the Underlying Asset
 Derivatives Also Help Reduce Market Transaction Costs

11. Market equilibrium
 Market equilibrium is a market state where the supply in
the market is equal to the demand in the market.
 The equilibrium price is the price of a good or service
when the supply of it is equal to the demand for it in the
market.
 If a market is at equilibrium, the price will not change
unless an external factor changes the supply or demand,
which results in a disruption of the equilibrium.

12.  The operation of the market depends on the interaction
between suppliers and demanders.
 Market equilibrium exists when quantity supplied is equal
to quantity demanded.
 Note that there is just one price where this is true!
 The equilibrium price is the price that will generally
prevail in a perfectly competitive market that is not
subject to governmental intervention.
 When a market is in equilibrium, there is no tendency for
the market price to change. In other words, the
equilibrium price is stable under the existing market
conditions.

13. 1.

14. Marginal Revenue
 Marginal revenue ( MR ) is the change in total revenue
resulting from selling an extra unit of goods.
 MR = TR/Q, where TR = change in TR due to
change in Q, Q = change in Q

15. Price elasticity of supply
 Price elasticity of supply (PES) measures the responsiveness of
quantity supplied to a change in price.
 It is necessary for a firm to know how quickly, and effectively,
it can respond to changing market conditions, especially to
price changes.
 The following equation can be used to calculate PES.
 While the coefficient for PES is positive in value, it may range
from 0, perfectly inelastic, to infinite, perfectly elastic.
2.

16. Income Elasticity Demand
 The Income Elasticity of Demand measures the rate of
response of quantity demand due to a raise (or lowering)
in a consumers income.
 The formula for the Income Elasticity of Demand (IEoD)
is given by:
 IEoD = (% Change in Quantity Demanded)/(%
Change in Income)

17. How Do We Interpret the Income Elasticity of Demand?
 Income elasticity of demand is used to see how sensitive
the demand for a good is to an income change.
 The higher the income elasticity, the more sensitive
demand for a good is to income changes.
 A very high income elasticity suggests that when a
consumer's income goes up, consumers will buy a great
deal more of that good.
 A very low price elasticity implies just the opposite, that
changes in a consumer's income has little influence on
demand.

18. Elasticity of Supply
 We can study the resulting changes in the supply of a
commodity, when its price changes, using the elasticity of
supply.
 Elasticity of supply is defined as
Elasticity of supply = relative change in supply /
relative change in price
 If the supply function is x = g (p), the elasticity of supply
є is given by
Elasticity of supply = (p/x ). (dx/ dp)

19.  Suppose P0 is the initial price of a commodity and X0 is
its supply.
 Suppose, when the price becomes p1 the supply becomes
s1.
 In this case, the elasticity of supply is given by
 Elasticity of supply є =
1 01 2
1 2 1 0
x xp p
p p x x


 

20. Marginal Revenue
 Marginal revenue is defined as follows:
 Marginal Revenue (M. R.) =
Change in total revenue / Change in demand
 If the demand function is p = f(x), then the total revenue R
is given by R = xp = x. f(x).
 The first derivative of R w.r.t. ‘x’ is called the marginal
revenue .
 Thus, M.R. = dR / dx.

21. Relation between average revenue, Marginal
revenue and Price elasticity of demand,
 There is a crucial relationship between the AR, MR and
elasticity of demand, which is used extensively in the
theory of pricing.
 The relationship is expressed in the form of formula,

22. 3.

23. But, AQ is marginal revenue and SQ is average revenue
corresponding to point ‘B’ at OQ level of output.
Hence, equation (2.9) can be written as
4.

24. The above relationship can be utilised to find out the
marginal revenue corresponding to the average revenue
at any given level of quantity sold, provided the price
elasticity of demand is known.
The relation between AR, MR and elasticity of
demand (e) can now be written as
5.

25. Maximum and Minimum Values
DEFINITION:
 A function f has an absolute maximum (or global
maximum) at c if f(c) ≥ f(x) for all x in D, where D is the
domain of f.
 The number f(c) is called the maximum value of f on D.
 Similarly, f has an absolute minimum (or global
minimum) at c if f(c) ≤ f(x) for all x in D and the number
f(c) is called the minimum value of f on D.
 The maximum and minimum values of f are called the
extreme values of f.

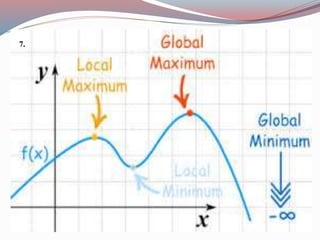
26. DEFINITION:
 A function f has a local maximum (or relative maximum)
at c if f(c) ≥ f(x) when x is near c.
 [This means that f(c) ≥ f(x) for all x in some open interval
containing c.]
 Similarly, f has a local minimum (or relative minimum) at
c if f(c) ≤ f(x) when x is near c.

27. 6.

28. 7.

29. Profit-maximizing
 The profit-maximizing level of output is a production
level that achieves the greatest level of economic
profit given existing market conditions and production
cost.
 For a perfectly competitive firm, this entails adjusting the
production level in response to the going market price.

30. Three Views
 Profit-maximizing output can be identified in one of three
ways--directly with economic profit, with a comparison
of total revenue and total cost, and with a comparison of
marginal revenue and marginal cost.

31. (1) Profit:
 First, profit maximization can be illustrated with a
direct evaluation of profit. If the profit curve is at its
peak, then profit is maximized.
 In the top panel, the profit curve achieves its highest
level at 7 pounds of zucchinis. At other output levels,
profit is less
8.

32. (2) Total Revenue and Total Cost:
• Second, profit maximization can
be identified by a comparison of
total revenue and total cost.
•The quantity of output that
achieves the greatest difference of
total revenue over total cost is profit
maximization.
•In the middle panel, the vertical
gap between the total revenue and
total cost curves is the greatest at 7
pounds of zucchinis.
•For smaller or larger output levels,
the gap is either less or the total cost
curve lies above the total revenue
curve.
9.

33. (3) Marginal Revenue and Marginal Cost:
•Third, profit maximization can be identified
by a comparison of marginal revenue and
marginal cost.
•If marginal revenue is equal to marginal cost,
then profit cannot be increased by changing the
level of production.
•Increasing production adds more to cost than
revenue, meaning profit declines.
•Decreasing production subtracts more from
revenue than from cost, meaning profit also
declines.
•In the bottom panel, the marginal revenue and
marginal cost curves intersect at 7 pounds of
zucchinis.
•At larger or smaller output levels, marginal
cost exceeds marginal revenue or marginal
revenue exceeds marginal cost.
10.

34. Cost Minimization
Strategies:
 Cost minimization aims to achieve the most cost-effective
way of delivering goods and services to the required level
of quality

35. Two approaches to cost minimization
(1) Possible sources of cost reductions (1):
 Eliminating waste & avoiding duplication ( lean
production )
 Simplifying processes and procedures
 Outsourcing non-core activities (e.g. transaction
processing, payroll, call handling)
 Negotiating better pricing with suppliers

36. (2) Possible sources of cost reductions (2)
 Pruning product ranges and customer accounts to
eliminate unprofitable business
 Using the most effective methods of training and
recruitment
 Introducing flexible working practices
 Aggressive control of overheads (e.g. banning
first/business class travel)

37. References:
1.https://lh3.ggpht.com/4jGqQc8XqZ8YrsVQ6LG0cPWEDDZnsqPM
a_zElCl2jWnA1reUw1H53VvUTahTpDsFqylfdw=s110
2.https://lh6.ggpht.com/IwP2fWoHPdaGqS_7mTM9xMT2VibScixvst
nvfvDkV2FDxbos_bcydDknlfylMJ04kM4dKw=s170.
3.https://lh6.ggpht.com/SHhJAGE4Fr4xXx7OpJPP2IOXx5yu7v7oY6
LvDZgq_anJKyRqPN4zwU03TQKKNUHwWg=s95.
4.https://lh6.ggpht.com/Lb7MNLpKXHaPudD_16mEoFlr1eVa8nPl7F
QlciKafgjBDvrLCxYgK4uFkicKPCNfvM7agQ=s170
5.https://lh6.ggpht.com/SHhJAGE4Fr4xXx7OpJPP2IOXx5yu7v7oY6
LvDZgq_anJKyRqPN4z-wU03TQKKNUHwWg=s95
6.https://lh6.ggpht.com/KaYAXA_Wzq8B5S7tF0TCZzbgIkFd9SrkR
Y9VGw0ld_0HPi7hqIpN_z8eCgAp-8eBxLncXg=s114

38. 7.https://lh5.ggpht.com/EiVgOUFxNQ_WubV8Y1Rl84bkUMrd
kmkjfutANj7Sd_cmeQTcWVQJpjy9iPboWXcauITw=s135
8. https://lh5.ggpht.com/eIXqTyak-aF0bimeguqNRGJN5UN71-
5qsCWuJ5Bj-J0tt6bO_IXhsb-o2_RSviygwVHQg=s135
9.https://lh3.ggpht.com/mvp5ltydSYbE2o46kzwIfMY99bgDtKZ
Wvbcm_SvOAH9wMZSugUSYymSOtLelaQaCxJxLSI=s89
10.https://lh3.ggpht.com/zmgXy_Je603OaHZNvbYjQQUNJ7TP
aWh3fBZChjle1vS1ERB-At3aCiinvnEmlia7AsfrRg=s89
11. Business Mathematics by A. G. Patel and G.C Patel – Atul
Prakashan.

39. Web Sources:
 www.thefreedictionary.com/implicit+function
 www.yourarticlelibrary.com/.../price-elasticity/...average-
revenue-margin.
 economics.about.com/cs/micfrohelp/a/supply_elast.htm
 http://en.wikipedia.org/wiki/Profit_maximization