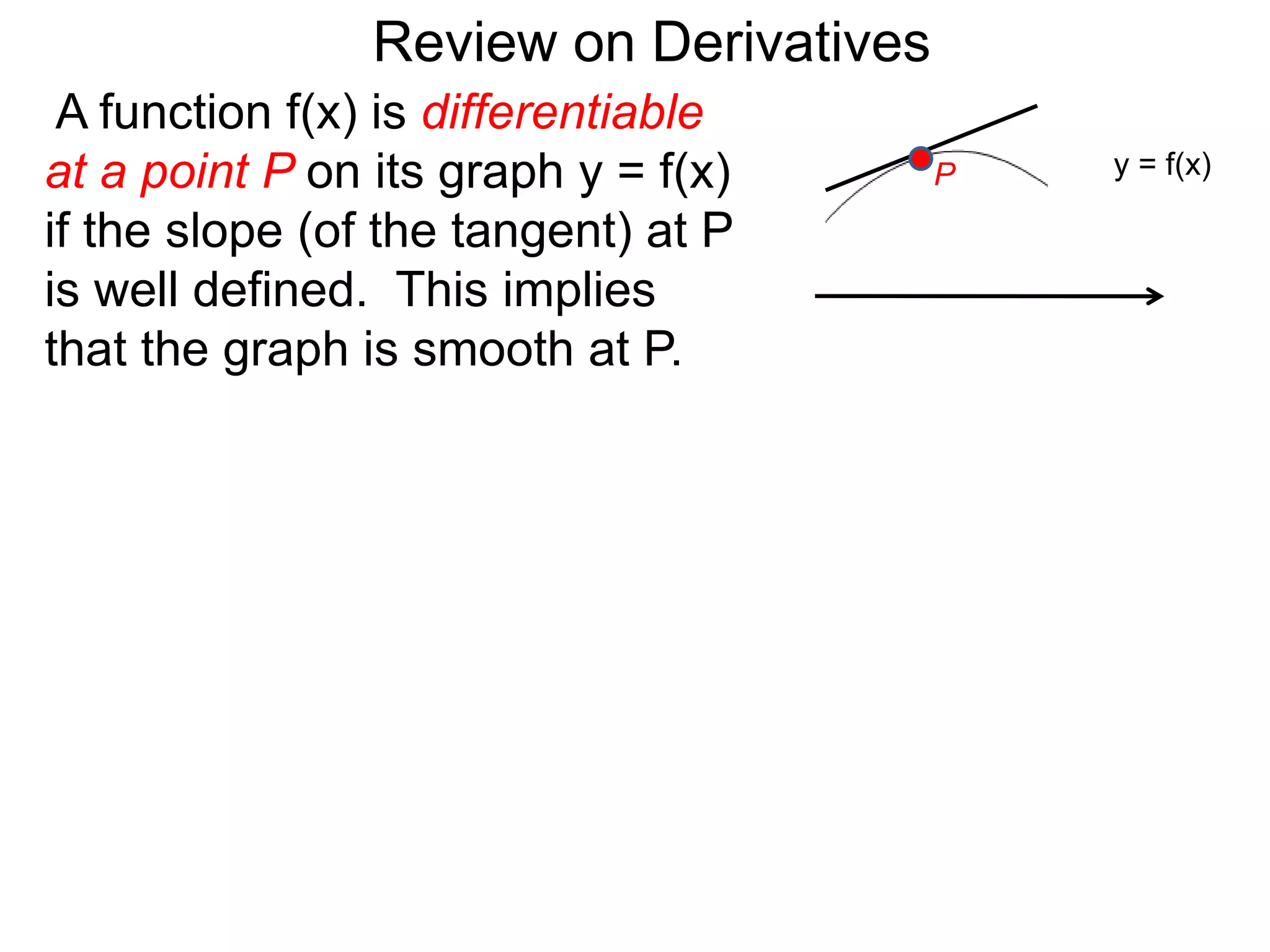
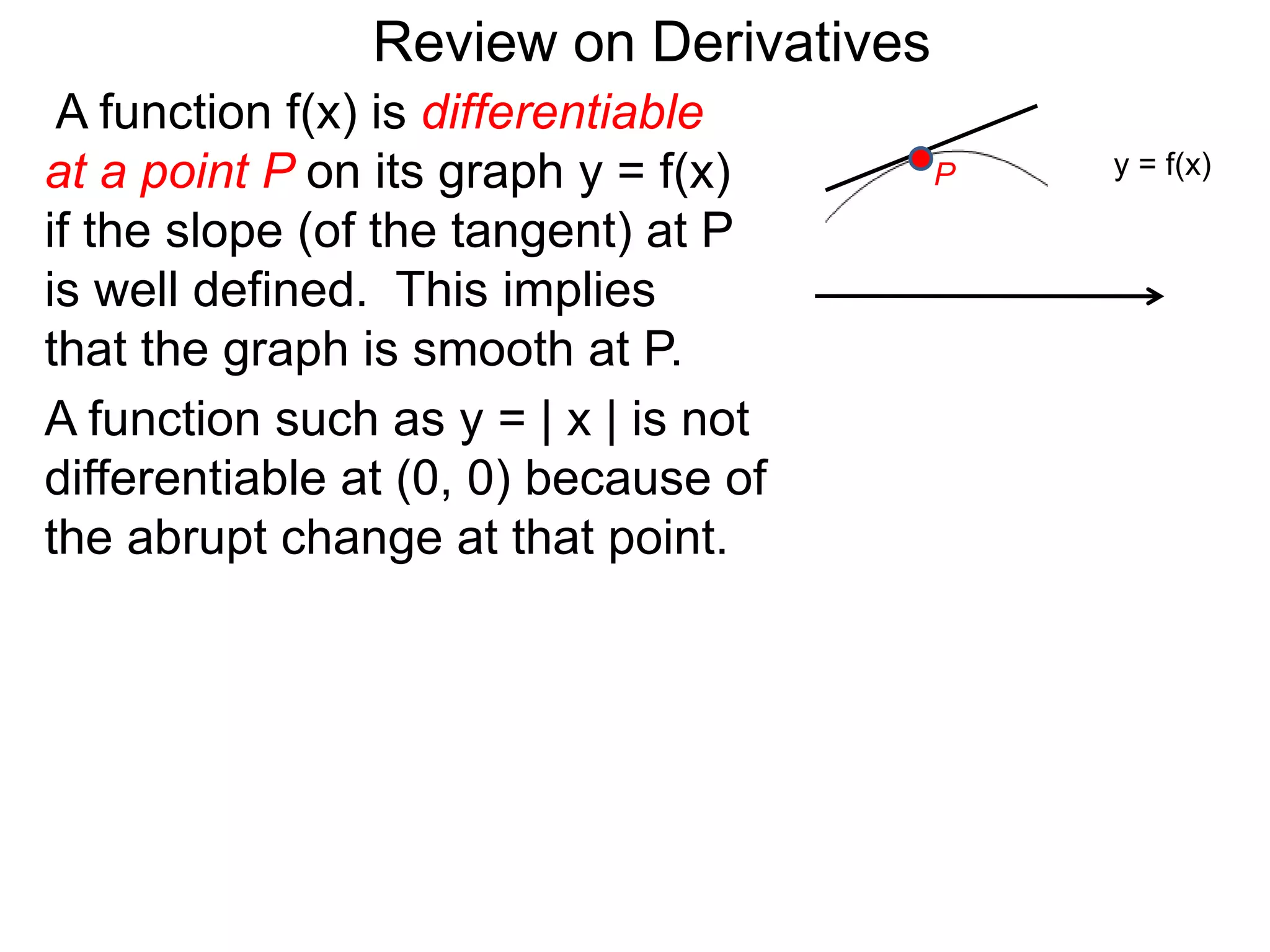
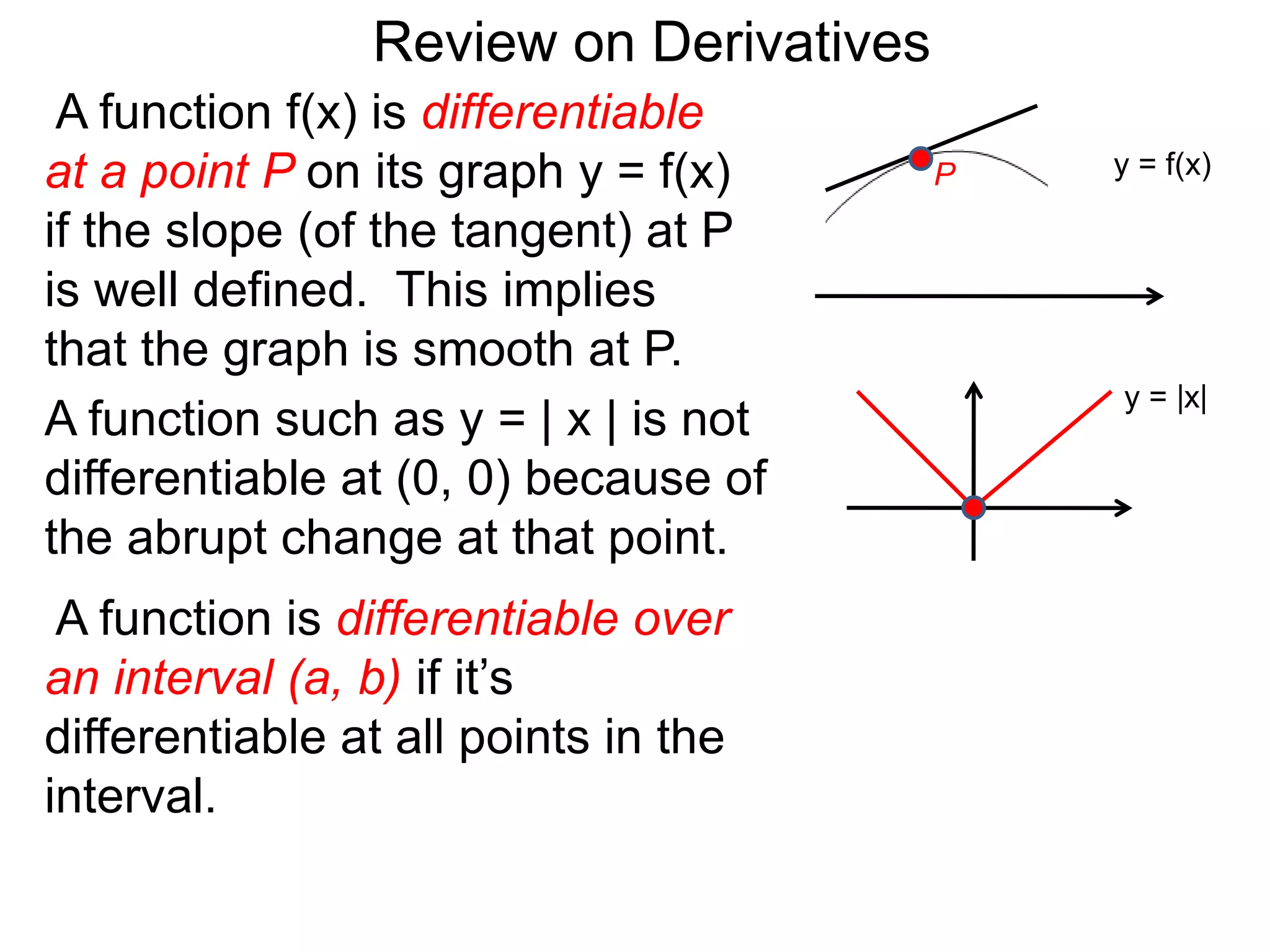
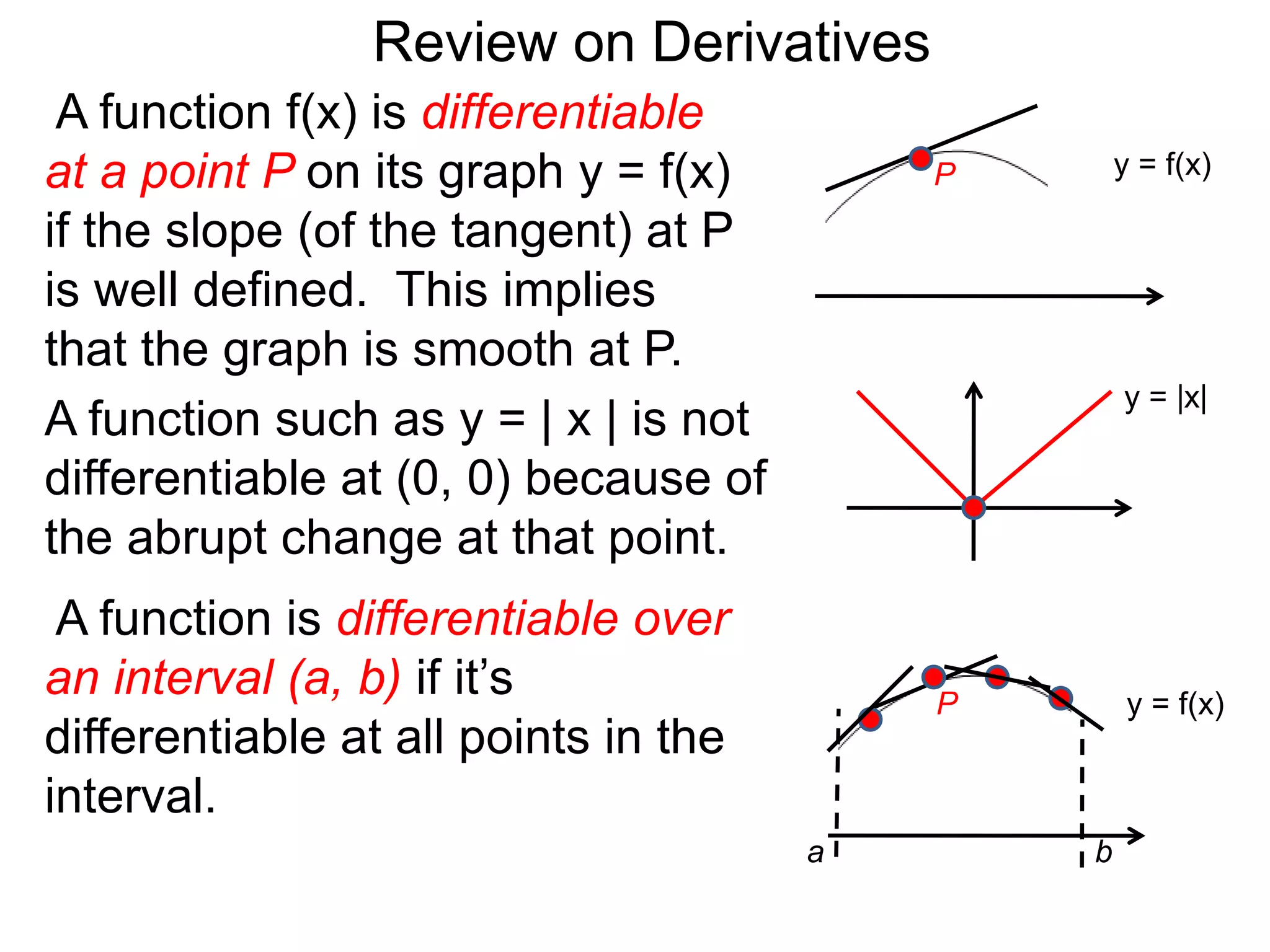
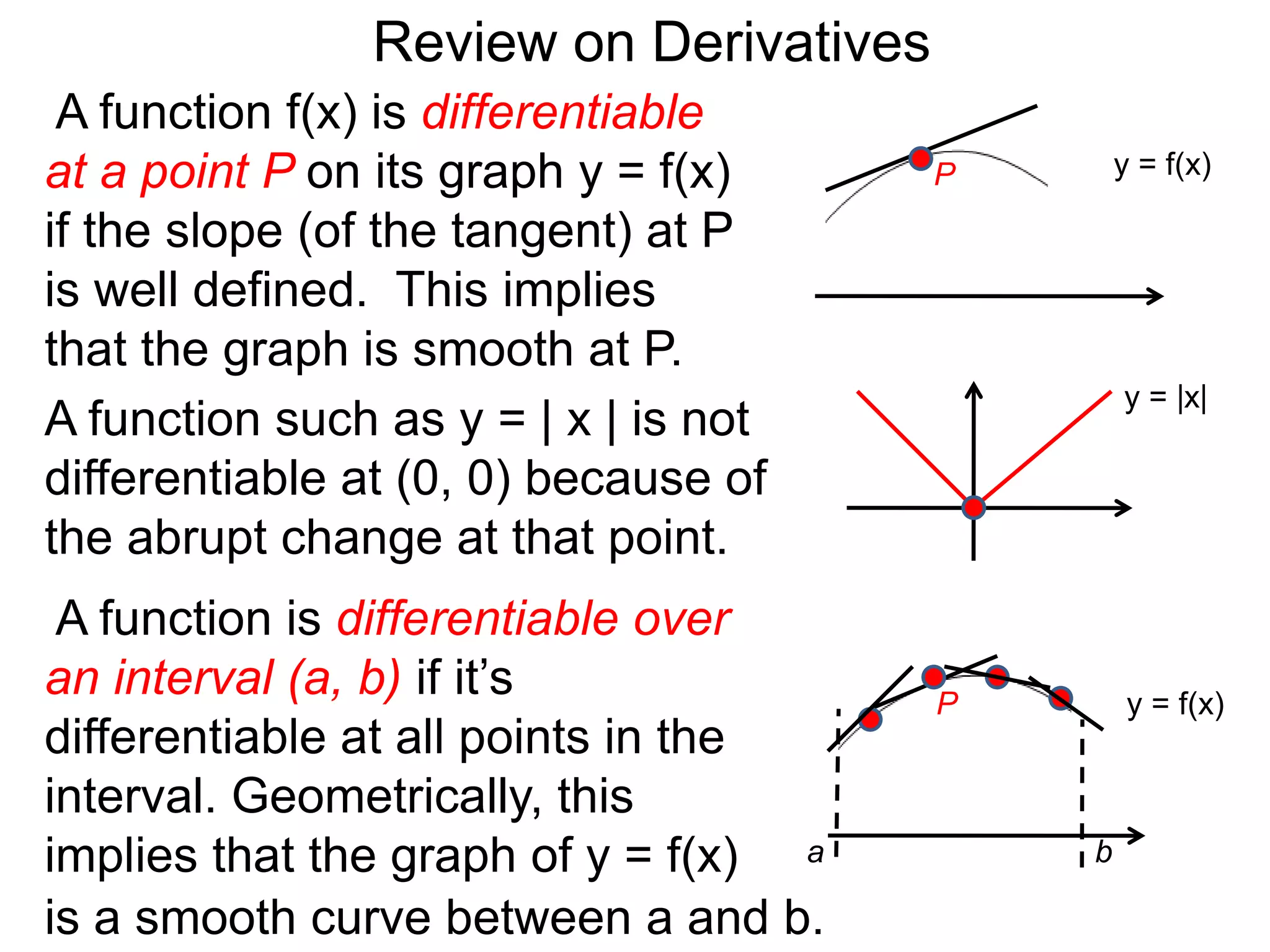
The document provides an overview of the concept of derivatives. It states that a function is differentiable at a point if the slope of its tangent line at that point is well-defined. It also notes that a function is differentiable over an interval if it is differentiable at every point in the interval. The document then discusses how derivatives can be systematically calculated by taking the derivatives of basic functions like power, trigonometric, logarithmic and exponential functions, and understanding how derivatives behave under operations like addition, subtraction, multiplication, division and function composition.

1. Review on Derivatives
http://www.lahc.edu/math/frankma.htm

2. A function f(x) is differentiable
at a point P on its graph y = f(x)
if the slope (of the tangent) at P
is well defined.
Review on Derivatives

3. A function f(x) is differentiable
at a point P on its graph y = f(x)
if the slope (of the tangent) at P
is well defined.
y = f(x)
Review on Derivatives
P

4. A function f(x) is differentiable
at a point P on its graph y = f(x)
if the slope (of the tangent) at P
is well defined. This implies
that the graph is smooth at P.
y = f(x)
Review on Derivatives
P

5. A function f(x) is differentiable
at a point P on its graph y = f(x)
if the slope (of the tangent) at P
is well defined. This implies
that the graph is smooth at P.
A function such as y = | x | is not
differentiable at (0, 0) because of
the abrupt change at that point.
y = f(x)
Review on Derivatives
P

6. A function f(x) is differentiable
at a point P on its graph y = f(x)
if the slope (of the tangent) at P
is well defined. This implies
that the graph is smooth at P.
A function such as y = | x | is not
differentiable at (0, 0) because of
the abrupt change at that point.
y = f(x)
y = |x|
Review on Derivatives
P

7. A function f(x) is differentiable
at a point P on its graph y = f(x)
if the slope (of the tangent) at P
is well defined. This implies
that the graph is smooth at P.
A function such as y = | x | is not
differentiable at (0, 0) because of
the abrupt change at that point.
y = f(x)
y = |x|
A function is differentiable over
an interval (a, b) if it’s
differentiable at all points in the
interval.
Review on Derivatives
P

8. A function f(x) is differentiable
at a point P on its graph y = f(x)
if the slope (of the tangent) at P
is well defined. This implies
that the graph is smooth at P.
A function such as y = | x | is not
differentiable at (0, 0) because of
the abrupt change at that point.
y = f(x)
y = |x|
A function is differentiable over
an interval (a, b) if it’s
differentiable at all points in the
interval.
Review on Derivatives
P
y = f(x)P
a b

9. A function f(x) is differentiable
at a point P on its graph y = f(x)
if the slope (of the tangent) at P
is well defined. This implies
that the graph is smooth at P.
A function such as y = | x | is not
differentiable at (0, 0) because of
the abrupt change at that point.
y = f(x)
y = |x|
A function is differentiable over
an interval (a, b) if it’s
differentiable at all points in the
interval. Geometrically, this
implies that the graph of y = f(x)
Review on Derivatives
P
y = f(x)P
a b
is a smooth curve between a and b.

10. Review of Derivatives
The slopes–formula of the graph for y = f(x) may be
“derived” from f(x).

11. Review of Derivatives
The slopes–formula of the graph for y = f(x) may be
“derived” from f(x). Therefore it’s called the derivative
of f(x) and it’s denoted as f ’(x) or .df
dx

12. Review of Derivatives
The slopes–formula of the graph for y = f(x) may be
“derived” from f(x). Therefore it’s called the derivative
of f(x) and it’s denoted as f ’(x) or .df
dx
y = f(x)P
x

13. Review of Derivatives
The slopes–formula of the graph for y = f(x) may be
“derived” from f(x). Therefore it’s called the derivative
of f(x) and it’s denoted as f ’(x) or .df
dx
y = f(x)P
f ’(x) = slope of
the tangent at x
x

14. Review of Derivatives
The slopes–formula of the graph for y = f(x) may be
“derived” from f(x). Therefore it’s called the derivative
of f(x) and it’s denoted as f ’(x) or .df
dx
Rules for Finding the Derivatives
y = f(x)P
f ’(x) = slope of
the tangent at x
x

15. Review of Derivatives
The slopes–formula of the graph for y = f(x) may be
“derived” from f(x). Therefore it’s called the derivative
of f(x) and it’s denoted as f ’(x) or .df
dx
Rules for Finding the Derivatives
The slope at a generic point
P = (x, y) is the limit as h  0
of the difference quotient (slope),
y = f(x)P
f ’(x) = slope of
the tangent at x
x

16. Review of Derivatives
The slopes–formula of the graph for y = f(x) may be
“derived” from f(x). Therefore it’s called the derivative
of f(x) and it’s denoted as f ’(x) or .df
dx
Rules for Finding the Derivatives
The slope at a generic point
P = (x, y) is the limit as h  0
of the difference quotient (slope),
y = f(x)Pi.e. f ’(x)≡ lim Δy
Δxh  0
f ’(x) = slope of
the tangent at x
x

17. Review of Derivatives
The slopes–formula of the graph for y = f(x) may be
“derived” from f(x). Therefore it’s called the derivative
of f(x) and it’s denoted as f ’(x) or .df
dx
Rules for Finding the Derivatives
The slope at a generic point
P = (x, y) is the limit as h  0
of the difference quotient (slope),
f(x + h) – f(x)
h
y = f(x)Pi.e. f ’(x)
h  0
≡ lim Δy
Δxh  0
≡ lim
f ’(x) = slope of
the tangent at x
x

18. Review of Derivatives
The slopes–formula of the graph for y = f(x) may be
“derived” from f(x). Therefore it’s called the derivative
of f(x) and it’s denoted as f ’(x) or .df
dx
Rules for Finding the Derivatives
The slope at a generic point
P = (x, y) is the limit as h  0
of the difference quotient (slope),
f(x + h) – f(x)
h
The existence of this limit means that we are able to
“balance” a tangent line at P and that the limit is the
slope of this line.
y = f(x)Pi.e. f ’(x)
h  0
≡ lim Δy
Δxh  0
≡ lim
f ’(x) = slope of
the tangent at x
x

19. Review of Derivatives
Elementary mathematics functions are functions built
from three basic families.

20. Review of Derivatives
Elementary mathematics functions are functions built
from three basic families.
* the power functions xp

21. Review of Derivatives
Elementary mathematics functions are functions built
from three basic families.
* the power functions xp
* the trig. functions such as sin(x), cos(x) and their
inverses arcsin(x), arccos(x)

22. Review of Derivatives
Elementary mathematics functions are functions built
from three basic families.
* the power functions xp
* the trig. functions such as sin(x), cos(x) and their
inverses arcsin(x), arccos(x)
* the log–function ln(x) and exponential functions ex.

23. Review of Derivatives
Elementary mathematics functions are functions built
from three basic families.
* the power functions xp
* the trig. functions such as sin(x), cos(x) and their
inverses arcsin(x), arccos(x)
* the log–function ln(x) and exponential functions ex.
New formulas are constructed from these basic ones,
with real numbers, using the algebraic operations
+, – , *, / , and the composition operation “○” of
functions.

24. Review of Derivatives
Elementary mathematics functions are functions built
from three basic families.
* the power functions xp
* the trig. functions such as sin(x), cos(x) and their
inverses arcsin(x), arccos(x)
* the log–function ln(x) and exponential functions ex.
New formulas are constructed from these basic ones,
with real numbers, using the algebraic operations
+, – , *, / , and the composition operation “○” of
functions.
Hence, to calculate derivatives systematically we find
I. the derivatives of the basic functions,

25. Review of Derivatives
Elementary mathematics functions are functions built
from three basic families.
* the power functions xp
* the trig. functions such as sin(x), cos(x) and their
inverses arcsin(x), arccos(x)
* the log–function ln(x) and exponential functions ex.
New formulas are constructed from these basic ones,
with real numbers, using the algebraic operations
+, – , *, / , and the composition operation “○” of
functions
Hence, to calculate derivatives systematically we find
I. the derivatives of the basic functions,
II. understand how the operations +, – , *, / and
function composition behave under differentiation.

26. Review of Derivatives
The basic derivatives that we know up to now are

27. Review of Derivatives
(Derivatives of xp)
The basic derivatives that we know up to now are

28. Review of Derivatives
(Derivatives of xp)
(Derivatives of the trigonometric functions)
dsin(x)
dx
dcos(x)
dx
dtan(x)
dx
dcot(x)
dx
dsec(x)
dx
dcsc(x)
dx
The basic derivatives that we know up to now are

29. Review of Derivatives
(Derivatives of xp)
If f(x) = xp then f ’(x) = pxp–1 or dxp
dx = pxp–1
(Derivatives of the trigonometric functions)
dsin(x)
dx = cos(x)
dcos(x)
dx = –sin(x)
dtan(x)
dx = sec2(x)
dcot(x)
dx = –csc2(x)
dsec(x)
dx = sec(x) tan(x)
dcsc(x)
dx = –csc(x)cot(x)
The basic derivatives that we know up to now are

30. Review of Derivatives
(Derivatives of xp)
If f(x) = xp then f ’(x) = pxp–1 or dxp
dx = pxp–1
(Derivatives of the trigonometric functions)
dsin(x)
dx = cos(x)
dcos(x)
dx = –sin(x)
dtan(x)
dx = sec2(x)
dcot(x)
dx = –csc2(x)
dsec(x)
dx = sec(x) tan(x)
dcsc(x)
dx = –csc(x)cot(x)
The basic derivatives that we know up to now are
Derivatives “respect” the operations of +, – , and
constant multiplication.

31. Review of Derivatives
(Derivatives of xp)
If f(x) = xp then f ’(x) = pxp–1 or dxp
dx = pxp–1
(Derivatives of the trigonometric functions)
dsin(x)
dx = cos(x)
dcos(x)
dx = –sin(x)
dtan(x)
dx = sec2(x)
dcot(x)
dx = –csc2(x)
dsec(x)
dx = sec(x) tan(x)
dcsc(x)
dx = –csc(x)cot(x)
The basic derivatives that we know up to now are
Derivatives “respect” the operations of +, – , and
constant multiplication.
But for the operations *, /, and function–composition,
the derivative behaves differently.

32. Review of Derivatives
(Derivatives of xp)
If f(x) = xp then f ’(x) = pxp–1 or dxp
dx = pxp–1
(Derivatives of the trigonometric functions)
dsin(x)
dx = cos(x)
dcos(x)
dx = –sin(x)
dtan(x)
dx = sec2(x)
dcot(x)
dx = –csc2(x)
dsec(x)
dx = sec(x) tan(x)
dcsc(x)
dx = –csc(x)cot(x)
The basic derivatives that we know up to now are
Derivatives “respect” the operations of +, – , and
constant multiplication.
But for the operations *, /, and function–composition,
the derivative behaves differently. Specifically,
derivative of composed–function obeys the Chain Rule.

33. Review of Derivatives
(Derivative Rules for ±, and Constant Multiplication.)
a. (cf) ’ = c(f) ’.
Let f = f(x), g = g(x) and c be a constant and that
the prime ( )’ operation means derivative taken with
respect to x.
b. (f ± g) ’ = (f) ’ ± (g) ’.

34. Review of Derivatives
(Derivative Rules for ±, and Constant Multiplication.)
a. (cf) ’ = c(f) ’.
Let f = f(x), g = g(x) and c be a constant and that
the prime ( )’ operation means derivative taken with
respect to x.
b. (f ± g) ’ = (f) ’ ± (g) ’.
These two facts may be phrased together as
(af ± bg) ’ = a(f) ’ ± b(g)’ where a and b are numbers.

35. Review of Derivatives
(Derivative Rules for ±, and Constant Multiplication.)
a. (cf) ’ = c(f) ’.
Let f = f(x), g = g(x) and c be a constant and that
the prime ( )’ operation means derivative taken with
respect to x.
b. (f ± g) ’ = (f) ’ ± (g) ’.
These two facts may be phrased together as
(af ± bg) ’ = a(f) ’ ± b(g)’ where a and b are numbers.
Example A.
a. Find the derivative of (2sin(x) + x – 2)
3

36. Review of Derivatives
(Derivative Rules for ±, and Constant Multiplication.)
a. (cf) ’ = c(f) ’.
Let f = f(x), g = g(x) and c be a constant and that
the prime ( )’ operation means derivative taken with
respect to x.
b. (f ± g) ’ = (f) ’ ± (g) ’.
These two facts may be phrased together as
(af ± bg) ’ = a(f) ’ ± b(g)’ where a and b are numbers.
Example A.
a. Find the derivative of (2sin(x) + x – 2)
3
(2sin(x) + x – 2)
[ ]’3

37. Review of Derivatives
(Derivative Rules for ±, and Constant Multiplication.)
a. (cf) ’ = c(f) ’.
Let f = f(x), g = g(x) and c be a constant and that
the prime ( )’ operation means derivative taken with
respect to x.
b. (f ± g) ’ = (f) ’ ± (g) ’.
These two facts may be phrased together as
(af ± bg) ’ = a(f) ’ ± b(g)’ where a and b are numbers.
Example A.
a. Find the derivative of (2sin(x) + x – 2)
3
(2sin(x) + x – 2) 1
[ ]’= 33
[2sin(x) + x – 2] ’

38. Review of Derivatives
(Derivative Rules for ±, and Constant Multiplication.)
a. (cf) ’ = c(f) ’.
Let f = f(x), g = g(x) and c be a constant and that
the prime ( )’ operation means derivative taken with
respect to x.
b. (f ± g) ’ = (f) ’ ± (g) ’.
These two facts may be phrased together as
(af ± bg) ’ = a(f) ’ ± b(g)’ where a and b are numbers.
Example A.
a. Find the derivative of (2sin(x) + x – 2)
3
(2sin(x) + x – 2) 1
[ ]’= 33
[2sin(x) + x – 2] ’
1=
3
(2cos(x) + 1)

39. Review of Derivatives
b. Find the slope and the equation of the tangent line
at x = 0 for f(x) = .
(2sin(x) + x – 2)
3

40. Review of Derivatives
b. Find the slope and the equation of the tangent line
at x = 0 for f(x) = .
(2sin(x) + x – 2)
3
At x = 0, f(0) = –2/3, hence the tangent line is based
at (0, –2/3).

41. Review of Derivatives
b. Find the slope and the equation of the tangent line
at x = 0 for f(x) = .
(2sin(x) + x – 2)
3
At x = 0, f(0) = –2/3, hence the tangent line is based
at (0, –2/3). The slope of the tangent is
f ’(0)

42. Review of Derivatives
b. Find the slope and the equation of the tangent line
at x = 0 for f(x) = .
(2sin(x) + x – 2)
3
At x = 0, f(0) = –2/3, hence the tangent line is based
at (0, –2/3). The slope of the tangent is
1f ’(0) = 3
(2cos(x) + 1) | x=0

43. Review of Derivatives
b. Find the slope and the equation of the tangent line
at x = 0 for f(x) = .
(2sin(x) + x – 2)
3
At x = 0, f(0) = –2/3, hence the tangent line is based
at (0, –2/3). The slope of the tangent is
1f ’(0) = 3
(2cos(x) + 1) | x=0 = 1
So by the tangent line formula y = f(x0)’(x – x0) + y0
we have the tangent line as y = x – 2/3.

44. Review of Derivatives
b. Find the slope and the equation of the tangent line
at x = 0 for f(x) = .
(2sin(x) + x – 2)
3
At x = 0, f(0) = –2/3, hence the tangent line is based
at (0, –2/3). The slope of the tangent is
1f ’(0) = 3
(2cos(x) + 1) | x=0 = 1
So by the tangent line formula y = f(x0)’(x – x0) + y0
we have the tangent line as y = x – 2/3.
Graphically, there are 4 possibilities at P = (0, –2/3).

45. Review of Derivatives
b. Find the slope and the equation of the tangent line
at x = 0 for f(x) = .
(2sin(x) + x – 2)
3
At x = 0, f(0) = –2/3, hence the tangent line is based
at (0, –2/3). The slope of the tangent is
1f ’(0) = 3
(2cos(x) + 1) | x=0 = 1
So by the tangent line formula y = f(x0)’(x – x0) + y0
we have the tangent line as y = x – 2/3.
Graphically, there are 4 possibilities at P = (0, –2/3).
P

46. Review of Derivatives
b. Find the slope and the equation of the tangent line
at x = 0 for f(x) = .
(2sin(x) + x – 2)
3
At x = 0, f(0) = –2/3, hence the tangent line is based
at (0, –2/3). The slope of the tangent is
1f ’(0) = 3
(2cos(x) + 1) | x=0 = 1
So by the tangent line formula y = f(x0)’(x – x0) + y0
we have the tangent line as y = x – 2/3.
Graphically, there are 4 possibilities at P = (0, –2/3).
P
P

47. Review of Derivatives
b. Find the slope and the equation of the tangent line
at x = 0 for f(x) = .
(2sin(x) + x – 2)
3
At x = 0, f(0) = –2/3, hence the tangent line is based
at (0, –2/3). The slope of the tangent is
1f ’(0) = 3
(2cos(x) + 1) | x=0 = 1
So by the tangent line formula y = f(x0)’(x – x0) + y0
we have the tangent line as y = x – 2/3.
Graphically, there are 4 possibilities at P = (0, –2/3).
P
P
P

48. Review of Derivatives
b. Find the slope and the equation of the tangent line
at x = 0 for f(x) = .
(2sin(x) + x – 2)
3
At x = 0, f(0) = –2/3, hence the tangent line is based
at (0, –2/3). The slope of the tangent is
1f ’(0) = 3
(2cos(x) + 1) | x=0 = 1
So by the tangent line formula y = f(x0)’(x – x0) + y0
we have the tangent line as y = x – 2/3.
Graphically, there are 4 possibilities at P = (0, –2/3).
P
P
P P

49. Review of Derivatives
b. Find the slope and the equation of the tangent line
at x = 0 for f(x) = .
(2sin(x) + x – 2)
3
At x = 0, f(0) = –2/3, hence the tangent line is based
at (0, –2/3). The slope of the tangent is
1f ’(0) = 3
(2cos(x) + 1) | x=0 = 1
So by the tangent line formula y = f(x0)’(x – x0) + y0
we have the tangent line as y = x – 2/3.
Graphically, there are 4 possibilities at P = (0, –2/3).
P
P
Ex. Which is it (without graphing it or using the 2nd
derivative)? Hint: Examine f ’(x) at 0+ and 0-.
P P

50. Review of Derivatives
(The Product and Quotient Rules for Derivative .)
Let f = f(x), g = g(x) and that the prime ( )’ operation
means derivative taken with respect to x, then
(fg)’ =
f
g( )’=

51. Review of Derivatives
(The Product and Quotient Rules for Derivative .)
Let f = f(x), g = g(x) and that the prime ( )’ operation
means derivative taken with respect to x, then
(fg)’ = (f)’g + f(g)’ (The Product Rule)
f
g( )’=

52. Review of Derivatives
(The Product and Quotient Rules for Derivative .)
Let f = f(x), g = g(x) and that the prime ( )’ operation
means derivative taken with respect to x, then
f
g( )’=
g2
g(f)’ – f(g)’
(fg)’ = (f)’g + f(g)’ (The Product Rule)
(The Quotient Rule)

53. Review of Derivatives
(The Product and Quotient Rules for Derivative .)
Let f = f(x), g = g(x) and that the prime ( )’ operation
means derivative taken with respect to x, then
f
g( )’=
g2
g(f)’ – f(g)’
(fg)’ = (f)’g + f(g)’ (The Product Rule)
(The Quotient Rule)
Example B. Find the derivative.
a. x2cos(x)

54. Review of Derivatives
(The Product and Quotient Rules for Derivative .)
Let f = f(x), g = g(x) and that the prime ( )’ operation
means derivative taken with respect to x, then
f
g( )’=
g2
g(f)’ – f(g)’
(fg)’ = (f)’g + f(g)’ (The Product Rule)
(The Quotient Rule)
Example B. Find the derivative.
a. x2cos(x)
[x2cos(x)]’

55. Review of Derivatives
(The Product and Quotient Rules for Derivative .)
Let f = f(x), g = g(x) and that the prime ( )’ operation
means derivative taken with respect to x, then
f
g( )’=
g2
g(f)’ – f(g)’
(fg)’ = (f)’g + f(g)’ (The Product Rule)
(The Quotient Rule)
Example B. Find the derivative.
a. x2cos(x)
[x2cos(x)]’
= (x2)’cos(x) + x2[cos(x)]’

56. Review of Derivatives
(The Product and Quotient Rules for Derivative .)
Let f = f(x), g = g(x) and that the prime ( )’ operation
means derivative taken with respect to x, then
f
g( )’=
g2
g(f)’ – f(g)’
(fg)’ = (f)’g + f(g)’ (The Product Rule)
(The Quotient Rule)
Example B. Find the derivative.
a. x2cos(x)
[x2cos(x)]’
= (x2)’cos(x) + x2[cos(x)]’
= 2xcos(x) – x2sin(x)

57. Review of Derivatives
(The Product and Quotient Rules for Derivative .)
Let f = f(x), g = g(x) and that the prime ( )’ operation
means derivative taken with respect to x, then
f
g( )’=
g2
g(f)’ – f(g)’
(fg)’ = (f)’g + f(g)’ (The Product Rule)
(The Quotient Rule)
Example B. Find the derivative.
a. x2cos(x)
[x2cos(x)]’
= (x2)’cos(x) + x2[cos(x)]’
= 2xcos(x) – x2sin(x)
b. cos(x)
x2

58. Review of Derivatives
(The Product and Quotient Rules for Derivative .)
Let f = f(x), g = g(x) and that the prime ( )’ operation
means derivative taken with respect to x, then
f
g( )’=
g2
g(f)’ – f(g)’
(fg)’ = (f)’g + f(g)’ (The Product Rule)
(The Quotient Rule)
Example B. Find the derivative.
a. x2cos(x)
[x2cos(x)]’
= (x2)’cos(x) + x2[cos(x)]’
= 2xcos(x) – x2sin(x)
b. cos(x)
x2
[ cos(x)
x2
]’

59. Review of Derivatives
(The Product and Quotient Rules for Derivative .)
Let f = f(x), g = g(x) and that the prime ( )’ operation
means derivative taken with respect to x, then
f
g( )’=
g2
g(f)’ – f(g)’
(fg)’ = (f)’g + f(g)’ (The Product Rule)
(The Quotient Rule)
Example B. Find the derivative.
a. x2cos(x)
[x2cos(x)]’
= (x2)’cos(x) + x2[cos(x)]’
= 2xcos(x) – x2sin(x)
b. cos(x)
x2
[ cos(x)
x2
]’
=
cos2(x)

60. Review of Derivatives
(The Product and Quotient Rules for Derivative .)
Let f = f(x), g = g(x) and that the prime ( )’ operation
means derivative taken with respect to x, then
f
g( )’=
g2
g(f)’ – f(g)’
(fg)’ = (f)’g + f(g)’ (The Product Rule)
(The Quotient Rule)
Example B. Find the derivative.
a. x2cos(x)
[x2cos(x)]’
= (x2)’cos(x) + x2[cos(x)]’
= 2xcos(x) – x2sin(x)
b. cos(x)
x2
[ cos(x)
x2
]’
=
cos2(x)
cos(x)(x2)’

61. Review of Derivatives
(The Product and Quotient Rules for Derivative .)
Let f = f(x), g = g(x) and that the prime ( )’ operation
means derivative taken with respect to x, then
f
g( )’=
g2
g(f)’ – f(g)’
(fg)’ = (f)’g + f(g)’ (The Product Rule)
(The Quotient Rule)
Example B. Find the derivative.
a. x2cos(x)
[x2cos(x)]’
= (x2)’cos(x) + x2[cos(x)]’
= 2xcos(x) – x2sin(x)
b. cos(x)
x2
[ cos(x)
x2
]’
=
cos2(x)
cos(x)(x2)’ – (cos(x))’x2

62. Review of Derivatives
(The Product and Quotient Rules for Derivative .)
Let f = f(x), g = g(x) and that the prime ( )’ operation
means derivative taken with respect to x, then
f
g( )’=
g2
g(f)’ – f(g)’
(fg)’ = (f)’g + f(g)’ (The Product Rule)
(The Quotient Rule)
Example B. Find the derivative.
a. x2cos(x)
[x2cos(x)]’
= (x2)’cos(x) + x2[cos(x)]’
= 2xcos(x) – x2sin(x)
b. cos(x)
x2
[ cos(x)
x2
]’
=
cos2(x)
cos(x)(x2)’ – (cos(x))’x2
=
cos2(x)
2xcos(x) + x2sin(x)

63. Review of Derivatives
(Derivative Rule for Composition–The Chain Rule)

64. Review of Derivatives
(Derivative Rule for Composition–The Chain Rule)
The Chain Rule gives the multiplying effect of the
rates of change under composition.

65. Review of Derivatives
(Derivative Rule for Composition–The Chain Rule)
The Chain Rule gives the multiplying effect of the
rates of change under composition. For instance,
let u = f(x) = 5x and y = g(u) = 3u.

66. Review of Derivatives
(Derivative Rule for Composition–The Chain Rule)
The Chain Rule gives the multiplying effect of the
rates of change under composition. For instance,
let u = f(x) = 5x and y = g(u) = 3u. The slope of u = 5x
is 5,

67. Review of Derivatives
(Derivative Rule for Composition–The Chain Rule)
The Chain Rule gives the multiplying effect of the
rates of change under composition. For instance,
let u = f(x) = 5x and y = g(u) = 3u. The slope of u = 5x
is 5, and the slope of y = g(u) = 3u as a function of u
is 3.

68. Review of Derivatives
(Derivative Rule for Composition–The Chain Rule)
The Chain Rule gives the multiplying effect of the
rates of change under composition. For instance,
let u = f(x) = 5x and y = g(u) = 3u. The slope of u = 5x
is 5, and the slope of y = g(u) = 3u as a function of u
is 3. The composition g(f(x)) where y is a function of x
is y = 3(5x) = 15x

69. Review of Derivatives
(Derivative Rule for Composition–The Chain Rule)
The Chain Rule gives the multiplying effect of the
rates of change under composition. For instance,
let u = f(x) = 5x and y = g(u) = 3u. The slope of u = 5x
is 5, and the slope of y = g(u) = 3u as a function of u
is 3. The composition g(f(x)) where y is a function of x
is y = 3(5x) = 15x which has a slope of (3)(5) = 15.

70. Review of Derivatives
(Derivative Rule for Composition–The Chain Rule)
The Chain Rule gives the multiplying effect of the
rates of change under composition. For instance,
let u = f(x) = 5x and y = g(u) = 3u. The slope of u = 5x
is 5, and the slope of y = g(u) = 3u as a function of u
is 3. The composition g(f(x)) where y is a function of x
is y = 3(5x) = 15x which has a slope of (3)(5) = 15.
(The Chain Rule)
Let u = f(x) and y = g(u) so that y = g(f(x)),
dy
dx =
dy
du
du
dx
then

71. Review of Derivatives
(Derivative Rule for Composition–The Chain Rule)
The Chain Rule gives the multiplying effect of the
rates of change under composition. For instance,
let u = f(x) = 5x and y = g(u) = 3u. The slope of u = 5x
is 5, and the slope of y = g(u) = 3u as a function of u
is 3. The composition g(f(x)) where y is a function of x
is y = 3(5x) = 15x which has a slope of (3)(5) = 15.
(The Chain Rule)
Let u = f(x) and y = g(u) so that y = g(f(x)),
dy
dx =
dy
du
du
dx
then
or [g(f(x))]’ = g’(f(x)) * f ’(x)

72. Review of Derivatives
(Derivative Rule for Composition–The Chain Rule)
The Chain Rule gives the multiplying effect of the
rates of change under composition. For instance,
let u = f(x) = 5x and y = g(u) = 3u. The slope of u = 5x
is 5, and the slope of y = g(u) = 3u as a function of u
is 3. The composition g(f(x)) where y is a function of x
is y = 3(5x) = 15x which has a slope of (3)(5) = 15.
(The Chain Rule)
Let u = f(x) and y = g(u) so that y = g(f(x)),
dy
dx =
dy
du
du
dx
then
or [g(f(x))]’ = g’(f(x)) * f ’(x)
derivative taken
with respect to x

73. Review of Derivatives
(Derivative Rule for Composition–The Chain Rule)
The Chain Rule gives the multiplying effect of the
rates of change under composition. For instance,
let u = f(x) = 5x and y = g(u) = 3u. The slope of u = 5x
is 5, and the slope of y = g(u) = 3u as a function of u
is 3. The composition g(f(x)) where y is a function of x
is y = 3(5x) = 15x which has a slope of (3)(5) = 15.
(The Chain Rule)
Let u = f(x) and y = g(u) so that y = g(f(x)),
dy
dx =
dy
du
du
dx
then
or [g(f(x))]’ = g’(f(x)) * f ’(x)
derivative taken
with respect to x
derivative taken
with respect to u

74. Review of Derivatives
(Derivative Rule for Composition–The Chain Rule)
The Chain Rule gives the multiplying effect of the
rates of change under composition. For instance,
let u = f(x) = 5x and y = g(u) = 3u. The slope of u = 5x
is 5, and the slope of y = g(u) = 3u as a function of u
is 3. The composition g(f(x)) where y is a function of x
is y = 3(5x) = 15x which has a slope of (3)(5) = 15.
(The Chain Rule)
Let u = f(x) and y = g(u) so that y = g(f(x)),
dy
dx =
dy
du
du
dx
then
or [g(f(x))]’ = g’(f(x)) * f ’(x)
derivative taken
with respect to x
derivative taken
with respect to u
derivative taken
with respect to x

75. Review of Derivatives
Example C. Let u = x2 and y = sin(u),
express y as a function of x and find dy/dx.

76. Review of Derivatives
Example C. Let u = x2 and y = sin(u),
express y as a function of x and find dy/dx.
y = sin(u) = sin(x2),

77. Review of Derivatives
Example C. Let u = x2 and y = sin(u),
express y as a function of x and find dy/dx.
y = sin(u) = sin(x2),
dy
dx =
dy
du
du
dx

78. Review of Derivatives
Example C. Let u = x2 and y = sin(u),
express y as a function of x and find dy/dx.
y = sin(u) = sin(x2),
dy
dx =
dy
du
du
dx
=
dsin(u)
du
dx2
dx

79. Review of Derivatives
Example C. Let u = x2 and y = sin(u),
express y as a function of x and find dy/dx.
y = sin(u) = sin(x2),
dy
dx =
dy
du
du
dx
=
dsin(u)
du
dx2
dx
= 2xcos(u)

80. Review of Derivatives
Example C. Let u = x2 and y = sin(u),
express y as a function of x and find dy/dx.
y = sin(u) = sin(x2),
dy
dx =
dy
du
du
dx
=
dsin(u)
du
dx2
dx
= 2xcos(u) = 2xcos(x2)

81. Review of Derivatives
Example C. Let u = x2 and y = sin(u),
express y as a function of x and find dy/dx.
y = sin(u) = sin(x2),
dy
dx =
dy
du
du
dx
=
dsin(u)
du
dx2
dx
= 2xcos(u) = 2xcos(x2)
Applying the chain rule to the basic functions yields
useful specific rules for calculation.

82. Review of Derivatives
Example C. Let u = x2 and y = sin(u),
express y as a function of x and find dy/dx.
y = sin(u) = sin(x2),
dy
dx =
dy
du
du
dx
=
dsin(u)
du
dx2
dx
= 2xcos(u) = 2xcos(x2)
let y = sin(u) and u = u(x) so that y = sin(u(x)),
Applying the chain rule to the basic functions yields
useful specific rules for calculation. For example,

83. Review of Derivatives
Example C. Let u = x2 and y = sin(u),
express y as a function of x and find dy/dx.
y = sin(u) = sin(x2),
dy
dx =
dy
du
du
dx
=
dsin(u)
du
dx2
dx
= 2xcos(u) = 2xcos(x2)
let y = sin(u) and u = u(x) so that y = sin(u(x)),
then [sin(u(x))]’
Applying the chain rule to the basic functions yields
useful specific rules for calculation. For example,
derivative taken
with respect to x

84. Review of Derivatives
Example C. Let u = x2 and y = sin(u),
express y as a function of x and find dy/dx.
y = sin(u) = sin(x2),
dy
dx =
dy
du
du
dx
=
dsin(u)
du
dx2
dx
= 2xcos(u) = 2xcos(x2)
let y = sin(u) and u = u(x) so that y = sin(u(x)),
then [sin(u(x))]’ = [sin(u)]’ * u(x)’
derivative taken
with respect to x
derivative taken
with respect to u
derivative taken
with respect to u
Applying the chain rule to the basic functions yields
useful specific rules for calculation. For example,

85. Review of Derivatives
Example C. Let u = x2 and y = sin(u),
express y as a function of x and find dy/dx.
y = sin(u) = sin(x2),
dy
dx =
dy
du
du
dx
=
dsin(u)
du
dx2
dx
= 2xcos(u) = 2xcos(x2)
let y = sin(u) and u = u(x) so that y = sin(u(x)),
then [sin(u(x))]’ = [sin(u)]’ * u(x)’ = cos(u)*(u)’.
derivative taken
with respect to x
derivative taken
with respect to u
derivative taken
with respect to u
Applying the chain rule to the basic functions yields
useful specific rules for calculation. For example,

86. Review of Derivatives
Similarly if u = u(x) and y = cos(u) or up, we get the
following specific chain rules formulas .

87. Review of Derivatives
Similarly if u = u(x) and y = cos(u) or up, we get the
following specific chain rules formulas .
a. [sin(u)]’ =
b. [cos(u)]’ =
c. [up] ’ =
(Specific Chain Rule Formulas)

88. Review of Derivatives
Similarly if u = u(x) and y = cos(u) or up, we get the
following specific chain rules formulas .
a. [sin(u)]’ = cos(u)*(u)’
b. [cos(u)]’ =
c. [up] ’ =
(Specific Chain Rule Formulas)

89. Review of Derivatives
Similarly if u = u(x) and y = cos(u) or up, we get the
following specific chain rules formulas .
a. [sin(u)]’ = cos(u)*(u)’
b. [cos(u)]’ = –sin(u)*(u)’
c. [up] ’ =
(Specific Chain Rule Formulas)

90. Review of Derivatives
Similarly if u = u(x) and y = cos(u) or up, we get the
following specific chain rules formulas .
a. [sin(u)]’ = cos(u)*(u)’
b. [cos(u)]’ = –sin(u)*(u)’
c. [up] ’ = pup–1(u)’
(Specific Chain Rule Formulas)

91. Review of Derivatives
Similarly if u = u(x) and y = cos(u) or up, we get the
following specific chain rules formulas .
a. [sin(u)]’ = cos(u)*(u)’
b. [cos(u)]’ = –sin(u)*(u)’
c. [up] ’ = pup–1(u)’
where u = u(x)
and ( )’ is the derivative with respect to x.
(Specific Chain Rule Formulas)

92. Review of Derivatives
Similarly if u = u(x) and y = cos(u) or up, we get the
following specific chain rules formulas .
a. [sin(u)]’ = cos(u)*(u)’
b. [cos(u)]’ = –sin(u)*(u)’
c. [up] ’ = pup–1(u)’
where u = u(x)
and ( )’ is the derivative with respect to x.
(Specific Chain Rule Formulas)
Example D. Find the derivative of cos[(x2+1)3]
(cos[(x2+1)3])’

93. Review of Derivatives
a. [sin(u)]’ = cos(u)*(u)’
b. [cos(u)]’ = –sin(u)*(u)’
c. [up] ’ = pup–1(u)’
where u = u(x)
and ( )’ is the derivative with respect to x.
Example D. Find the derivative of cos[(x2+1)3]
(cos[(x2+1)3])’
u(x)
Similarly if u = u(x) and y = cos(u) or up, we get the
following specific chain rules formulas .
(Specific Chain Rule Formulas)

94. Review of Derivatives
a. [sin(u)]’ = cos(u)*(u)’
b. [cos(u)]’ = –sin(u)*(u)’
c. [up] ’ = pup–1(u)’
where u = u(x)
and ( )’ is the derivative with respect to x.
Example D. Find the derivative of cos[(x2+1)3]
(cos[(x2+1)3])’ = –sin[u] [(x2+1)3] ’
u(x) u’
Similarly if u = u(x) and y = cos(u) or up, we get the
following specific chain rules formulas .
(Specific Chain Rule Formulas)

95. Review of Derivatives
a. [sin(u)]’ = cos(u)*(u)’
b. [cos(u)]’ = –sin(u)*(u)’
c. [up] ’ = pup–1(u)’
where u = u(x)
and ( )’ is the derivative with respect to x.
Example D. Find the derivative of cos[(x2+1)3]
(cos[(x2+1)3])’ = –sin[(x2+1)3] [(x2+1)3]’
Similarly if u = u(x) and y = cos(u) or up, we get the
following specific chain rules formulas .
(Specific Chain Rule Formulas)

96. Review of Derivatives
a. [sin(u)]’ = cos(u)*(u)’
b. [cos(u)]’ = –sin(u)*(u)’
c. [up] ’ = pup–1(u)’
where u = u(x)
and ( )’ is the derivative with respect to x.
Example D. Find the derivative of cos[(x2+1)3]
(cos[(x2+1)3])’ = –sin[(x2+1)3] [(x2+1)3]’
the new u(x) for u3
Similarly if u = u(x) and y = cos(u) or up, we get the
following specific chain rules formulas .
(Specific Chain Rule Formulas)

97. Review of Derivatives
a. [sin(u)]’ = cos(u)*(u)’
b. [cos(u)]’ = –sin(u)*(u)’
c. [up] ’ = pup–1(u)’
where u = u(x)
and ( )’ is the derivative with respect to x.
Example D. Find the derivative of cos[(x2+1)3]
(cos[(x2+1)3])’ = –sin[(x2+1)3] [(x2+1)3]’
the new u(x) for u3
= –sin[(x2+1)3] [3(x2+1)2] (x2+1)’
the new u’
Similarly if u = u(x) and y = cos(u) or up, we get the
following specific chain rules formulas .
(Specific Chain Rule Formulas)

98. Review of Derivatives
a. [sin(u)]’ = cos(u)*(u)’
b. [cos(u)]’ = –sin(u)*(u)’
c. [up] ’ = pup–1(u)’
where u = u(x)
and ( )’ is the derivative with respect to x.
Example D. Find the derivative of cos[(x2+1)3]
(cos[(x2+1)3])’ = –sin[(x2+1)3] [(x2+1)3]’
the new u(x) for u3
= –sin[(x2+1)3] [3(x2+1)2] (x2+1)’
the new u’
= –sin[(x2+1)3] [3(x2+1)2] 2x
Similarly if u = u(x) and y = cos(u) or up, we get the
following specific chain rules formulas .
(Specific Chain Rule Formulas)

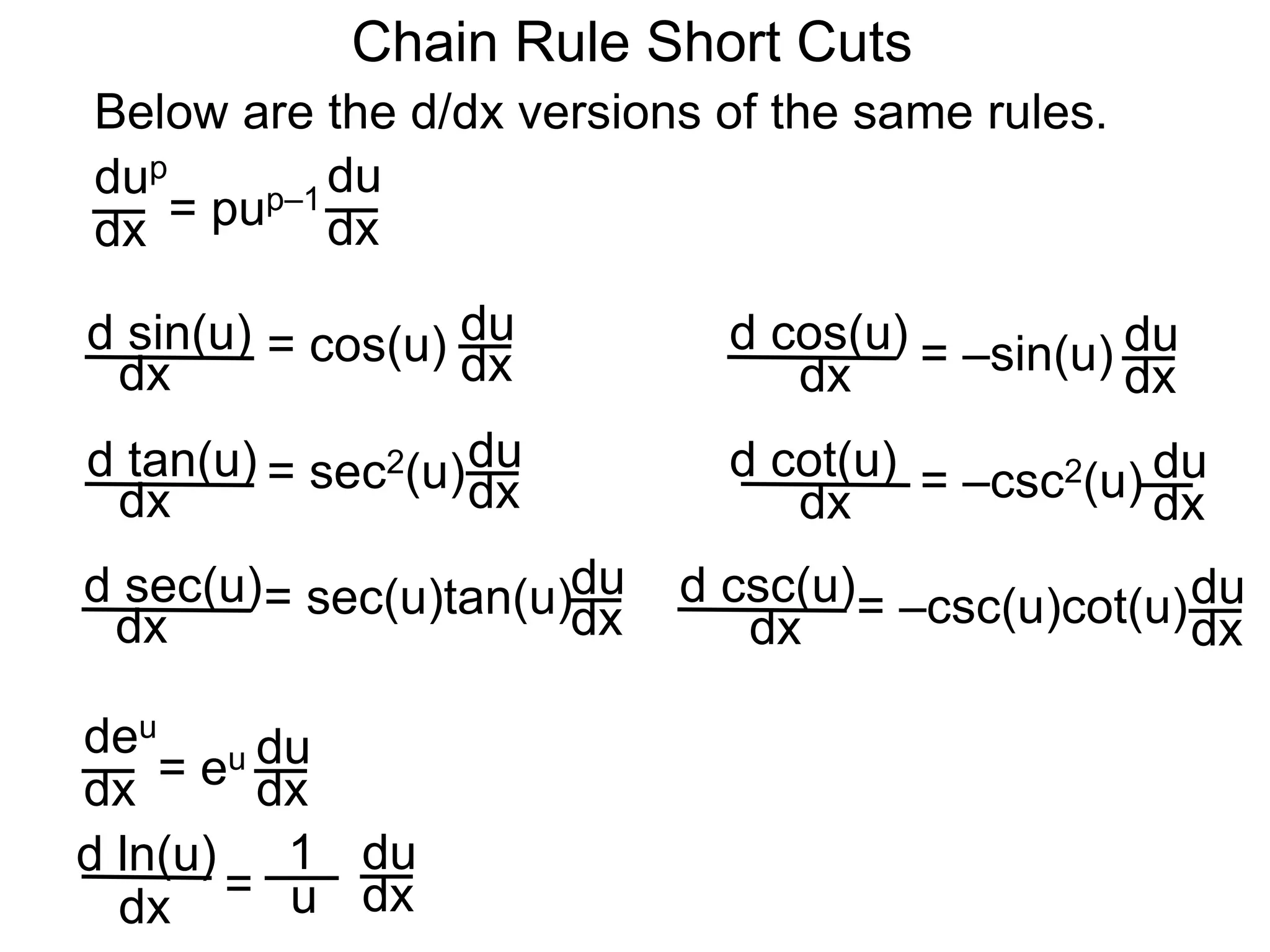
99. Chain Rule Short Cuts
[sin(u)] ' = sin'(u) = cos(u)(u)'
(Chain Rule Short Cuts)
(The Power Chain Rule)
[up]' = pup–1(u)'
(The Trig. Chain Rules)
[tan(u)] ' = tan'(u) = sec2(u)(u)'
[sec (u)] ' = sec'(u) = sec(u)tan(u)(u)'
[csc (u)] ' = csc'(u) = –csc(u)cot(u)(u)'
[cos(u)] ' = cos'(u) = –sin(u)(u)'
[cot(u)] ' = cot'(u) = –csc2(u)(u)'
(The Derivatives of Log and Exponential Functions)
and [eu]' = eu(u)'
and [ln(u)]' = (u)'
u
[ex]' = ex
[ln(x)]' = x
1

100. dup
dx
d sin(u)
dx
Chain Rule Short Cuts
Below are the d/dx versions of the same rules.
= pup–1
du
dx
= cos(u) du
dx
d cos(u)
dx = –sin(u) du
dx
d tan(u)
dx
= sec2(u)du
dx
d cot(u)
dx = –csc2(u) du
dx
d sec(u)
dx
= sec(u)tan(u)du
dx
d csc(u)
dx = –csc(u)cot(u)du
dx
deu
dx = eu du
dx
d ln(u)
dx =
du
dxu
1