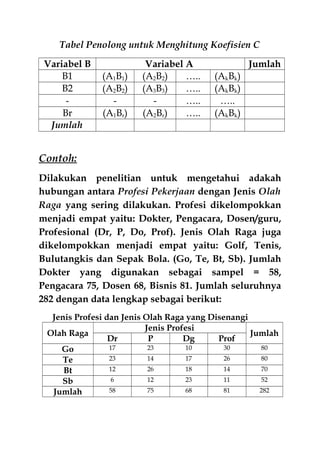
Dokumen tersebut membahas beberapa uji statistik nonparametrik untuk menguji hipotesis, yaitu: (1) Uji Chi Kuadrat untuk satu dan dua sampel yang digunakan untuk data nominal, (2) Koefisien kontingensi untuk mengukur hubungan antar variabel nominal. Contoh penerapannya adalah menguji apakah profesi pekerjaan berhubungan dengan jenis olahraga yang disenangi, yang menunjukkan adanya hubungan signifikan antara

1. Analisis Data Non-parametrik
1. Uji Chi Kuadrat (x2
) satu sampel
Chi kuadrat (x2
) satu sampel dapat digunakan
untuk menguji hipotesis populasi jika data sampelnya
berbentuk nominal atau data frekuensi. Rumus untuk
menghitung nilai x2
adalah:
Dimana:
x2
= Chi kuadrat
fp = frekuensi pengamatan
fh = frekuensis harapan
k = banyaknya kategori
Langkah-langkah pengujian hipotesis:
1. Rumuskan H0 dan H1 sesuai permasalahan yang
diteliti
2. Hitung statistik x2
(x2
hitung)
3. Tentukan nilai kritis (nilai x2
tabel) pada taraf
signifikansi α tertentu (α=0.01 atau 0.05), yaitu x2
tabel
= x2
(1-α; dk=k-1). Tentukan daerah kritis (daerah
penolakan Ho)

2. 4. Pengambilan keputusan
Dengan membandingkan nilai x2
hitung dengan x2
tabel
maka kesimpulannya adalah:
• Jika x2
hitung ≤ x2
tabel, maka terima H0
• Jika x2
hitung > x2
tabel, maka tolak H0
Contoh: Kasus Pilpres
Di suatu daerah pemilihan, salah satu lembaga survey
ingin mengetahui apakah politisi, pengusaha, atau
militer mempunyai peluang yang sama untuk menjadi
Presiden pada Pilpres 2009. Responden diminta untuk
memilih salah satu dari tiga kategori calon Presiden
yang diminati. Sampel sebagai sumber data diambil
secara random sebanyak 600 orang. Dari sampel
tersebut ternyata 225 orang memilih politisi, 165
orang memilih pengusaha, dan 210 orang memilih
militer. Ujilah hipotesis yang menyatakan bahwa
“ketiga kategori calon Presiden tidak mempunyai
peluang yang sama untuk dipilih”.
0 x2
tab
daerah kritis
α

3. Jawab:
1. Rumusan Hipotesis:
H0: Ketiga kategori calon Presiden mempunyai
peluang sama untuk dipilih.
H1: Ketiga kategori calon Presiden tidak
mempunyai peluang sama untuk dipilih.
2. Menghitung statistik x2
Tabel data frekuensi pengamatan dan frekuensi harapan
Kategori Calon Presiden
Jumlah
Politisi Pengusaha Militer
Frekuensi
pengamatan
(fp)
225 165 210 600
Frekuensi
harapan (fh)
200 200 200 600
Sehingga:
Jadi x2
hitung = 24.75

4. 3. Nilai kritis pada α= 0.05
x2
tabel = x2
(1-α; dk = k-1) = x2
(1-0.05; dk = 3-1) =x2
(0.95; 2)=5.99
4. Daerah kritis pada α= 0.05
5. Kesimpulan
Karena x2
hitung = 24.75 > x2
tabel = 5.99, atau jatuh pada
daerah kritis, maka Ho ditolak. Kita simpulkan
bahwa pada tingkat signifikansi α= 0.05, ketiga
kategori calon Presiden peluangnya tidak sama
untuk dipilih. Kalau dilihat frekuensi pengamatan
per kategori, maka calon Presiden yang berlatar
belakang politisi paling diminati masyarakat.
0 5.99

5. 2. Chi Square (x2
) dua sampel (Tabel
Kontingensi
Chi square dapat digunakan untuk menguji
hipotesis komparatif dua sampel yang tidak
berkorelasi bila datanya berbentuk nominal. Cara
perhitungannya dapat menggunakan Tabel
kontingensi 2 x 2 (dua baris x dua kolom) sebagai
berikut:
Tabel Kontingensi
Sampel
Frekuensi pada: Jumlah
SampelObjek I Objek II
Sampel A a b a+b
Sampel B c D c+d
Jumlah a+c b+d N
n = jumlah sampel
Rumus yang digunakan untuk menguji hipotesis,
adalah sebagai berikut:
Contoh: Kecenderungan pembaca dalam memilih
jenis Surat Kabar (Koran)
Penelitian dilakukan untuk mengetahui adakah
hubungan antara tingkat pendidikan masyarakat

6. dengan jenis koran yang dibaca. Pendidikan
masyarakat dikelompokkan menjadi dua, yaitu
lulusan SLTA dan Perguruan Tinggi (PT). Sampel
pertama sebanyak 80 orang lulusan SLTA dan sampel
kedua sebanyak 70 orang lulusan PT. Berdasarkan
angket yang diberikan kepada sampel lulusan SLTA,
maka dari 80 orang, yang memilih koran X sebanyak
60 orang, dan Koran Y sebanyak 20 orang. Selanjutnya
dari kelompok sampel lulusan PT, dari 70 orang, yang
memilih koran X sebanyak 30 orang dan koran Y
sebanyak 40 orang.
Berdasarkan hal tersebut:
1. Rumusan Hipotesis:
Ho: Tidak terdapat perbedaan tingkat pendidi-kan
masyarakat dalam memilih dua jenis koran
yang dibaca
H1: Terdapat perbedaan tingkat pendidikan
masyarakat dalam memilih dua jenis koran
yang dibaca
2. Menghitung nilai chi square
Data hasil penelitian tersebut selanjutnya disusun
ke dalam table sbb:
Sampel
Jenis Koran Jumlah
sampelKoran X Koran Y
Lulusan SLTA 60 20 80
Lulusan PT 30 40 70
Jumlah 90 60 150

7. Berdasarkan nilai dalam table tersebut, maka harga
Chi Kuadrat dapat dihitung:
3. Kriteria pengujian hipotesis:
Dengan taraf kesalahan 5%, dk= 1 maka harga x2
tabel
= 3.841. Ternyata nilai x2
hitung > nilai x2
tabel, dengan
demikian Ho ditolak dan H1 diterima.
4. Kesimpulan:
Jadi terdapat perbedaan tingkat pendidikan dalam
memilih jenis Surat Kabar yang dibaca, dimana
lulusan SLTA cenderung memilih Surat Kabar X
dan lulusan Perguruan Tinggi cenderung memilih
Surat Kabar Y.

8. Koefisien Kontingensi (Tabel Silang)
Koefisien kontingensi digunakan untuk menghitung
hubungan antar variabel bila dataya berbentuk
nominal. Teknik ini mempunyai kaitan erat dengan
Chi Kuadrat yang digunakan untuk menguji hipotesis
komparatif k sampel independen. Rumus yang
digunakan mengandung nilai Chi Kuadrat seperti
berikut:
Harga Chi Kuadrat dicari dengan rumus:
Keputusan penerimaan dan penolakan Ho pada taraf
signifikansi α diberikan adalah:
Jika X2
< X2
(1-α);(r-1)(k-1) maka terima Ho
Jika X2
≥ X2
(1-α);(r-1)(k-1) maka tolak Ho
Untuk memudahkan perhitungan, maka data-data
hasil penelitian perlu disusun ke dalam tabel yang
modelnya ditunjukkan pada tabel berikut:

9. Tabel Penolong untuk Menghitung Koefisien C
Variabel B Variabel A Jumlah
B1 (A1B1) (A2B2) ….. (AkBk)
B2 (A2B2) (A3B3) ….. (AkBk)
- - - ….. …..
Br (A1Br) (A2Br) ….. (AkBk)
Jumlah
Contoh:
Dilakukan penelitian untuk mengetahui adakah
hubungan antara Profesi Pekerjaan dengan Jenis Olah
Raga yang sering dilakukan. Profesi dikelompokkan
menjadi empat yaitu: Dokter, Pengacara, Dosen/guru,
Profesional (Dr, P, Do, Prof). Jenis Olah Raga juga
dikelompokkan menjadi empat yaitu: Golf, Tenis,
Bulutangkis dan Sepak Bola. (Go, Te, Bt, Sb). Jumlah
Dokter yang digunakan sebagai sampel = 58,
Pengacara 75, Dosen 68, Bisnis 81. Jumlah seluruhnya
282 dengan data lengkap sebagai berikut:
Jenis Profesi dan Jenis Olah Raga yang Disenangi
Olah Raga
Jenis Profesi
Jumlah
Dr P Dg Prof
Go 17 23 10 30 80
Te 23 14 17 26 80
Bt 12 26 18 14 70
Sb 6 12 23 11 52
Jumlah 58 75 68 81 282

10. Berdasarkan hal tersebut lakukan pengujian hipotesis
pada taraf kesalahan α = 0.05.
Pengujian Hipotesis:
1. Rumusan Hipotesis:
Ho: Tidak ada hubungan yang positif dan
signifikan antara jenis Profesi dengan jenis
Olahraga yang disenangi
H1: Ada hubungan yang positif dan signifikan
antara jenis Profesi dengan jenis olahraga yang
disenangi
2. Perhitungan Nilai Chi Kuadrat
Untuk menghitung frekuensi yang diharapkan (fh)
pertama-tama dihitung berapa persen dari masing-
masing sampel yang menyenangi olah raga Golf,
Tenis, Bulu Tangkis, dan Sepak Bola.
Dari sini dapat dihitung prosentase:
i. Keempat sampel yang menyenangi olah raga
golf, adalah:
ii. Keempat sampel yang menyenangi olahraga
tennis, adalah:

11. iii. Keempat sampel yang menyenangi olahraga
bulu tangkis, adalah:
iv. Keempat sampel yang menyenangi olahraga
sepak bola adalah:
Selanjutnya masing-masing fh (frekuensi yang
diharapkan) kelompok yang menyenangi setiap
jenis olah raga dapat dihitung:
a. Yang menyenangi golf:
1) fh Dokter = 0.284 x 58 = 16.472
2) fh Pengacara = 0.284 x 75 = 21.300
3) fh Dosen = 0.284 x 68 = 19.312
4) fh Bisnis = 0.284 x 81 = 23.004
=80
b. Yang menyenangi tennis:
1) fh Dokter = 0.284 x 58 = 16.472
2) fh Pengacara = 0.284 x 75 = 21.300

12. 3) fh Dosen = 0.284 x 68 = 19.312
4) fh Bisnis = 0.284 x 81 = 23.004
=80
c. Yang menyenangi bulu tangkis:
1) fh Dokter = 0.248 x 58 = 14.384
2) fh Pengacara = 0.248 x 75 = 18.600
3) fh Dosen = 0.248 x 68 = 16.864
4) fh Bisnis = 0.248 x 81 = 20.088
=70
d. Yang menyenangi sepak bola:
1) fh Dokter = 0.184 x 58 = 10.672
2) fh Pengacara = 0.184 x 75 = 13.800
3) fh Dosen = 0.184 x 68 = 12.512
4) fh Bisnis = 0.184 x 81 = 14.904
=52
Berdasarkan hasil perhitungan tersebut, selanjutnya
dimasukkan dalam tabel berikut:
Jenis Profesi dan Jenis Olah Raga yang Disenangi
Olah
Raga
Dr P Do Bi
Jml
fo fh fo fh fo fh fo fh
Go 17 16.472 23 21.300 10 19.312 30 23.004 80

13. Te 23 16.472 14 21.300 17 19.312 26 23.004 80
Bt 12 14.384 26 18.600 18 16.864 14 10.088 70
Sb 6 10.672 12 13.800 23 12.512 11 14.904 52
Jml 58 75 68 81 282
Selanjutnya harga Chi Kuadrat dapat dihitung dengan
rumus:
Dalam hal ini O (observation) = fo dan E (Expectation) = fh
x2
= 0.017 + 0.136 + 4.490 + 2.128 + 2.587 + 2.502 + 0.277 + 0.390 + 0.395 +
2.944+ 0.077 + 1.845 + 2.045 + 0.235 + 8.791 + 1.023
x2
= 29.881
Selanjutnya untuk menghitung koefisien kontingensi
C, maka harga tersebut dimasukkan dalam rumus
berikut:

14. Jadi besarnya koefisien antara jenis profesi dengan
kesenangan olah raga = 0.31.
3. Nilai kritis pada α = 0.05
Harga dk = (k-1) (r-1), k = jumlah sampel = 4 dan r =
jumlah kategori olahraga = 4. Jadi dk = (4-1)(4-1) = 9.
Berdasakan dk = 9 dan taraf kesalahan 0.05, maka
harga Chi Kuadrat tabel = 16.92. Karena nilai Chi
Kuadrat hitung lebih besar dari tabel (29.881 >
15.51) maka Ho ditolak dan H1 diterima.
4. Kesimpulan
Jenis profesi pekerjaan mempunyai hubungan
signifikan dengan jenis olahraga yang disenangi
sebesar 0.31.
Data yang ada pada sampel dan angka korelasi
mencerminkan keadaan populasi dimana sampel
diambil. Dari data terlihat 37% (30:81) pebisnis
cenderung menyenanagi Golf. Sedangkan hanya
14.7% (10:68) dosen yang menyenangi Golf. 33.3%
dosen menyenangi sepak bola (data fiktif).