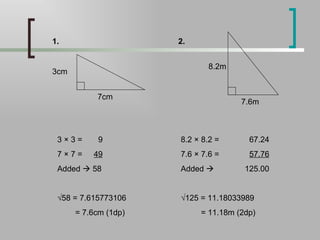
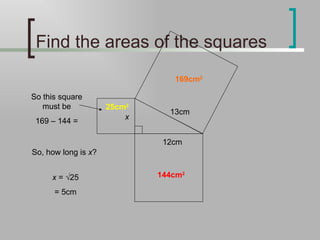
Pythagoras' theorem states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. The document explains how to use Pythagoras' theorem to find the length of any side of a right-angled triangle if the other two sides are known. It provides examples of calculating missing side lengths and notes that the theorem can be rearranged to find a non-hypotenuse side if the hypotenuse is known instead. Correct notation for showing working is emphasized.

1. Pythagoras’ Theorem Finding missing sides in Right-Angled Triangles

2. Introduction Pythagoras was a Greek (of course!) mathematician who worked out a simple way of calculating the length of any side of a right-angled triangle, using the lengths of the other two sides … if I know how long these sides are? How long is this side… for example… or…

3. How it works… Pythagoras discovered that the three sides of a right-angled triangle have a relationship to each other. He found that if you draw a square on each of the three sides, the area of the two smallest squares adds together to make the area of the biggest square. Look at the next slide to see what I mean...

4. The Pythagoras Relation… Now we all know that yellow plus red makes orange don’t we? Well, the two small squares , added together make the big square. Click here for puzzle

5. Here’s an example for you… How big is the side marked x ? Remember that the two small squares add to make the big one? So how big are the two small squares? x 3m 4m A=9m 2 A=16m 2

6. So how big is the biggest square? x 3m 4m A=9m 2 A=16m 2 A=25m 2 So, if the big square has an area of 25m 2 , what is the length of one of its sides? Side x would have to be 5m

7. Now try this one: What is the length of side x ? 5mm 12mm x

8. Draw squares on the sides. A= 25mm 2 A=144mm 2 5mm 12mm x What is the area of the x square? Remember that the two small squares add together to make the big one A=169mm 2

9. So how long is the side? The length of x is 13mm. This is because A= 25mm 2 A=144mm 2 A=169mm 2 5mm 12mm 5mm 12mm x

10. Now try these…. (the answers won’t be whole numbers so you will have to use the square root key ( ) on your calculator) 3cm 7cm 1. x 6 miles 2 miles 3. x 2.5km 3.8km 4. x 8.2m 7.6m 2. x

11. 3 × 3 = 9 7 × 7 = 49 Added  58 √ 58 = 7.615773106 = 7.6cm (1dp) 8.2 × 8.2 = 67.24 7.6 × 7.6 = 57.76 Added  125.00 √ 125 = 11.18033989 = 11.18m (2dp) 8.2m 7.6m 2. 3cm 7cm 1.

12. 2.5 × 2.5 = 6.25 3.8 × 3.8 = 14.44 Added  20.69 √ 20.69 = 4.5486261662 = 4.55km (2dp) 6 × 6 = 36 2 × 2 = 4 Added  40 √ 40 = 6.3245553203 = 6.3 miles (1dp) 2.5km 3.8km 4. 6 miles 2 miles 3.

13. Notation Remember that you will have to show in a test how you got these answers. Although the way that the answers were set out in the previous slides was clear, it’s better to set out your answers like this…

14. We know that a square on the x side is equal to the squares on the other two sides added together. So, that’s what we write… X 2 = 3 2 + 7 2 = 9 + 49 = 58 X = √58 = 7.615773 = 7.6cm (1dp) This line shows that the big square is equal to the two small squares added together. You can leave out this bit if you like, but always use units, round sensibly, and show your rounding. 3 cm 7 cm 1. x

15. Some exercises for you to try… Ex. Page Ex. Page Remember to always include units and round sensibly. A good guide is to round to one more decimal place than the measurements you have been given.

16. But what if…? Up until now, we have been finding the length of the hypotenuse, having been told the length of the other two sides. We know this side… … and this side… … and so we can find out this side.

17. But what if we already know the hypotenuse? What happens if we know the length of the hypotenuse, and we want to find the length of one of the other two sides? We know this side… … and this side… … and we want to find out this side.

18. Remember the idea of squares? Yellow plus Red makes Orange ! Well if the Yellow square plus the Red square equals the Orange square… … then the Orange square minus the Red square equals the Yellow square!

19. Here’s how we do this. 13cm 12cm x How long is side x ? Draw squares on the sides

20. Find the areas of the squares 169cm 2 144cm 2 25cm 2 So, how long is x ? x = √25 = 5cm 13cm 12cm x So this square must be 169 – 144 =

21. Remember Correct Notation… 13cm 12cm x X 2 = 13 2 - 12 2 = 169 - 144 = 25 X = √25 = 5cm (1dp)

22. Some exercises for you to try… Ex. Page Ex. Page Remember to always include units and round sensibly. A good guide is to round to one more decimal place than the measurements you have been given.