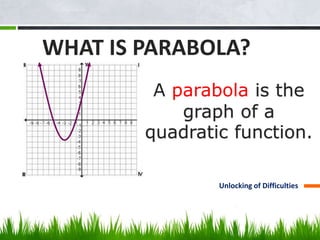
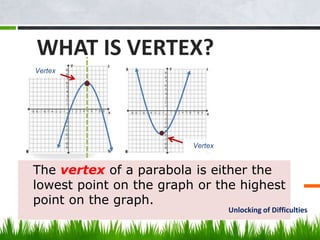
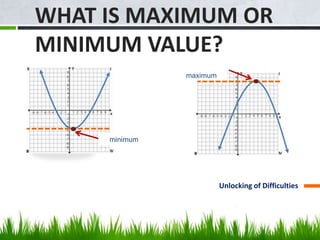
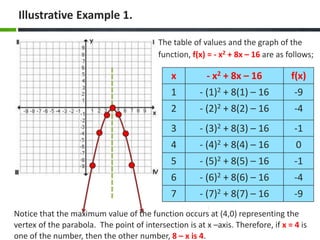
This document discusses solving problems involving quadratic functions. It provides examples of finding the maximum or minimum value of quadratic functions, including finding the dimensions of a rectangle that will maximize its area given a fixed perimeter. It also discusses key concepts related to quadratic functions like parabolas, vertices, axes of symmetry, and finding the zeros of a function. Examples are provided to illustrate solving problems requiring the application of these quadratic function concepts.

1. PROBLEM SOLVING
INVOLVING QUADRATIC
Reynaldo B. Pantino FUNCTION

2. Objectives:
Determine the
maximum or the
minimum value
of
f(x) =ax2 + bx
+ c.
Write the given
and the unknown
quantity of the
problem.
Solve and show
the solution of
solving the
problem.

3. A professional pyro-technician shoots fireworks vertically into
the air off of a building that is 80 feet tall. The initial 80 feet velocity tall
of
the firework initial velocity
is 64 feet per second.
64 feet per second
When
will the fireworks reach their maximum height?
What is the maximum height reached by the fireworks?
maximum height
h = –16t2 + v0t + h0
– b
2a
t =

4. WHAT IS PARABOLA?
A parabola is the
graph of a
quadratic function.
Unlocking of Difficulties

5. WHAT IS VERTEX?
Vertex
Vertex
The vertex of a parabola is either the
lowest point on the graph or the highest
point on the graph.
Unlocking of Difficulties

6. WHAT IS AXIS OF
SYMMETRY?
The axis of symmetry is the line that
divides the parabola into two equal
parts.
Unlocking of Difficulties
Axis of symmetry

7. WHAT IS MAXIMUM OR
MINIMUM VALUE?
When a parabola opens up and the vertex
is the lowest point the y-coordinate of the
vertex is the minimum.
When a parabola opens down and the
vertex is the highest point the y-coordinate
of the vertex is the maximum.
Unlocking of Difficulties

8. WHAT IS MAXIMUM OR
MINIMUM VALUE?
Unlocking of Difficulties
minimum
maximum

9. WHAT IS ZERO OF A
FUNCTION?
Zero of a function is a number x such
that f(x) = 0.
Example. F(x) = x2 – 4x + 4.
What is the value of x such that f(x) will
be zero?
Unlocking of Difficulties

10. Illustrative Example 1.
1. Find two real numbers whose sum is 8 and whose product is 16.
Solution:
Let x be one of the numbers. Then 8 – x is the other number. If the
product of the two numbers is 16, then,
x(8 – x) = 16
8x – x2 = 16
- x2 + 8x – 16 = 0 by factoring we have (x - 4)(-x + 4) = 0
x = 4 ( one of the number)
What is 8 – x ?
Since x = 4 then 8 – (4) = 4 (other number)

11. Illustrative Example 1.
The table of values and the graph of the
function, f(x) = - x2 + 8x – 16 are as follows;
x - x2 + 8x – 16 f(x)
1 - (1)2 + 8(1) – 16 -9
2 - (2)2 + 8(2) – 16 -4
3 - (3)2 + 8(3) – 16 -1
4 - (4)2 + 8(4) – 16 0
5 - (5)2 + 8(5) – 16 -1
6 - (6)2 + 8(6) – 16 -4
7 - (7)2 + 8(7) – 16 -9
Notice that the maximum value of the function occurs at (4,0) representing the
vertex of the parabola. The point of intersection is at x –axis. Therefore, if x = 4 is
one of the number, then the other number, 8 – x is 4.

12. Illustrative Example 2.
A projectile is launched from a point 40 meters above the
ground. The height at ground level h in meters after t
seconds is given by the function, h(t) = 40t – 5t2. How
many seconds after the launch will the projectile hit the
ground?
Solution:
At the ground level, the value of h will be 0. Thus,
the quadratic equation is; 0 = 40t – 5t2
0 = 40t – 5t2
0 = 5t(8 – t) by common factor
5t = 0 solve for the value of t
t = 0
8 – t = 0
t = 8

13. Illustrative Example 2.
Since t represents the time in seconds
after the launch, t ≠ 0. The projectile will
hit the ground 8 seconds after launch.
You can always solve this equation by
looking for the zeros of the related
quadratic function.
Axis of symmetry: Vertex
t = - b /2a h(t) = 40t – 5t2
= - 40/2(-5) h(4) = 40(4) – 5(4)2
= 4 = 80

14. 2 4 6 8
120
100
Axis of symmetry
80
60
40
20
0
Illustrative Example 2.
Thus, the vertex of the graph is the
point (4,80) where the maximum
value occurs. The graph and table of
values is given below;
x 40t – 5t2 f(x)
0 40(0) – 5(0)2 0
1 40(1) – 5(1)2 35
2 40(2) – 5(2)2 60
3 40(3) – 5(3)2 75
4 40(4) – 5(4)2 80
5 40(5) – 5(5)2 75
6 40(6) – 5(6)2 60
7 40(7) – 5(7)2 35
8 40(8) – 5(8)2 0
Maximum value
vertex
(4,80)

15. Illustrative Example 3.
One hundred meters of fencing is used to
fence a rectangular region. What
dimensions of the rectangle will maximize
the area of the region?
Solution:
The formula for the perimeter of a
rectangle is P = 2(l + w)
Since P = 100 meters, the length plus the
width is 50 meters.
Thus, let x be the length of the rectangle
50 – x is the width of the
rectangle
Since A = lw for the area of the rectangle,
A (x) = x(50 – x)
= 50x – x2
The area is a
quadratic function
of the length.
The maximum value
occurs when;
x = -b /2a
Thus; x = -50/2(-1)
= 25
The length should be
25 m and the width
should be 25 m. The
rectangle that gives
the maximum area is
a square with an
area of 625 m2.

16. Activity 1. Find the maximum or the minimum value of
each quadratic function
1.) f(x) = x2 – 5x + 6 6.) f(x) = -x2 + 4x – 3
2.) f(x) = x2 – 10x + 21 7.) f(x) = -x2 – 5x – 3
3.) f(x) = x2 – 6x – 6 8.) f(x) = -2x2 + 2x - 5
4.) f(x) = x2 – 2x + 4 9.) f(x) = 2x2 + 2x – 4
5.) f(x) = 2x2 – x + 6 10.) f(x) = 6x2 – x + 2

17. Activity 2. Solve at least 2 of the following problems.
1.) Find the two real numbers whose sum is 4 and whose product is a
maximum.
2.) The perimeter of a rectangle is 38 meters. Find the dimensions of
the rectangle that will contain the greatest area.
3.) Find the number of computer units x that needs to be sold to
produce a maximum profit P (in pesos) if P = 900x – 0.1x2.
4.) The height in feet of a ball t seconds after being tossed upwards is
given by the function h(t) = 84t – 16t2.
a. After how many seconds will it hit the ground?
b. What is its maximum height?
5.) The sum of two numbers is 22 and the sum of their squares is 250.
Find the numbers.

18. Quiz. (1 whole sheet of paper)
1. The sum of two numbers is 16 and the
sum of their squares is 146. Find the
numbers.
2. The perimeter of a rectangle is 138
meters and the area is 1080 square
meters. Find the length and the width of
the rectangle.