Embed presentation
Downloaded 150 times











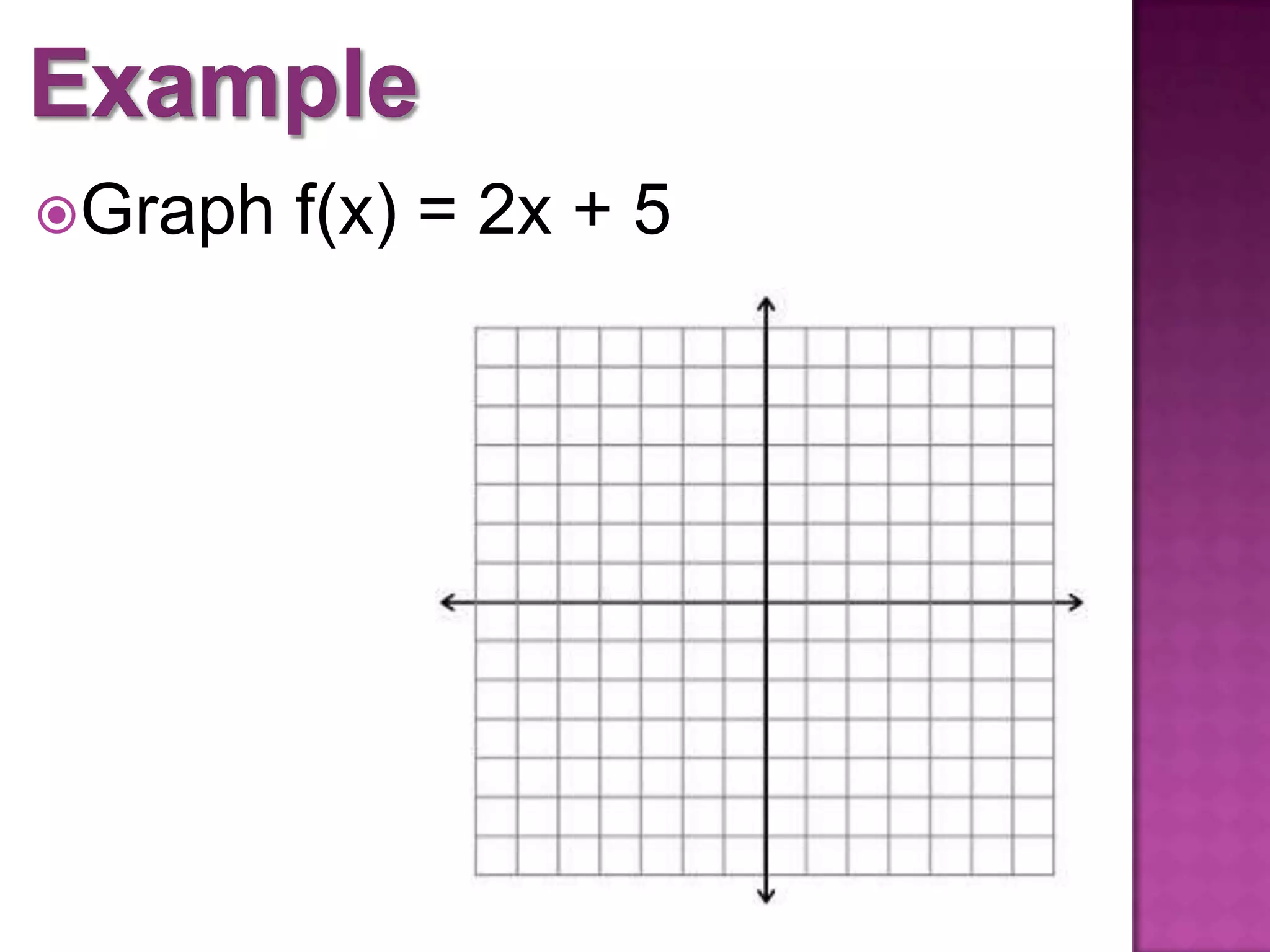
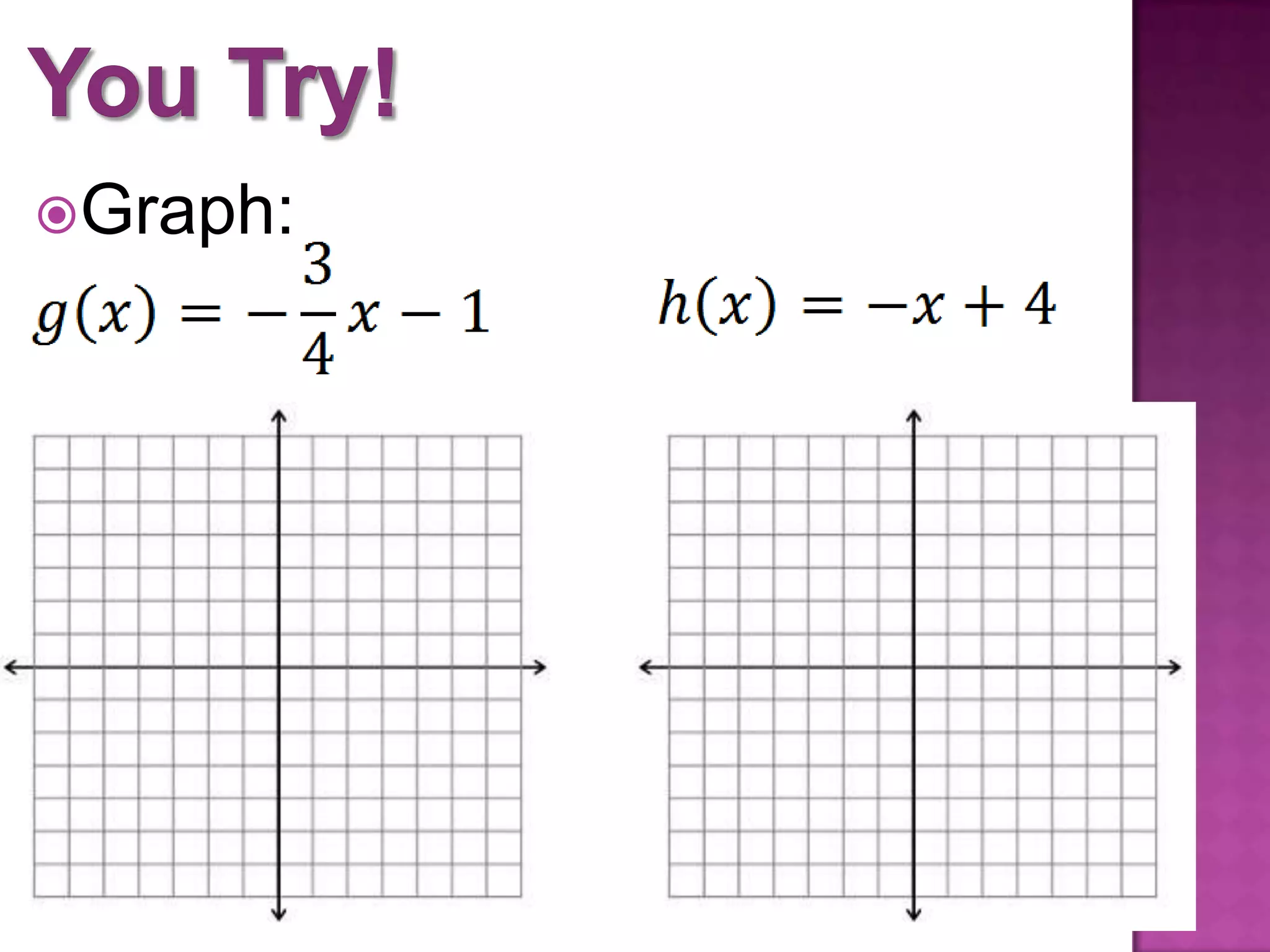
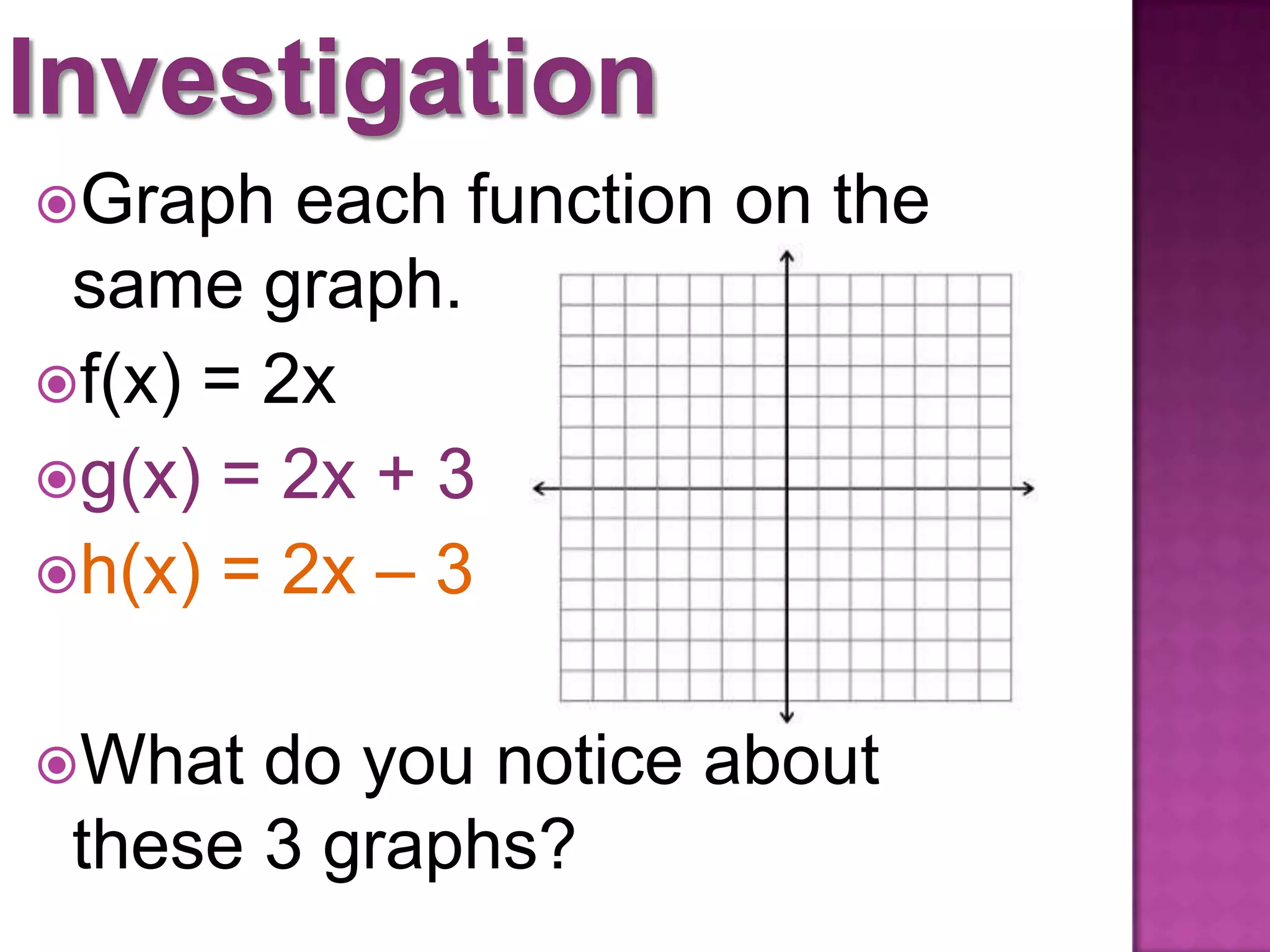

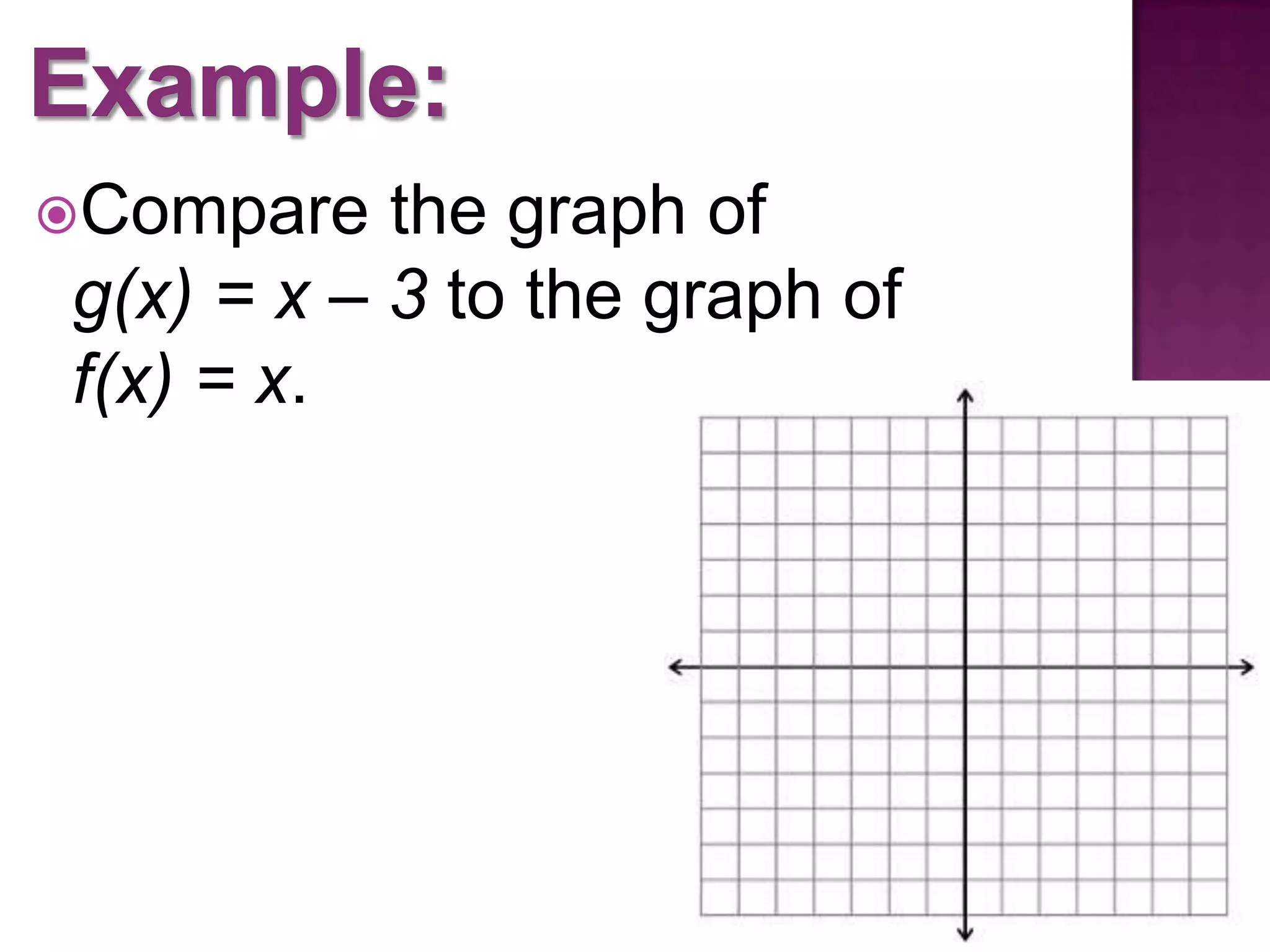
This document introduces function notation and how to evaluate functions. It explains that f(x) represents the output of the function f for a given input x. Examples show different functions defined using this notation, such as f(x) = 2x + 1. The document also demonstrates how to evaluate functions for given x-values, find x-values for which a function is a certain amount, and graph functions using this notation. It compares translating and shifting graphs of functions.
Introduction to linear functions using f(x) notation and examples with various function forms.
Methods to evaluate functions for specific x values, including examples of finding outputs for various functions.
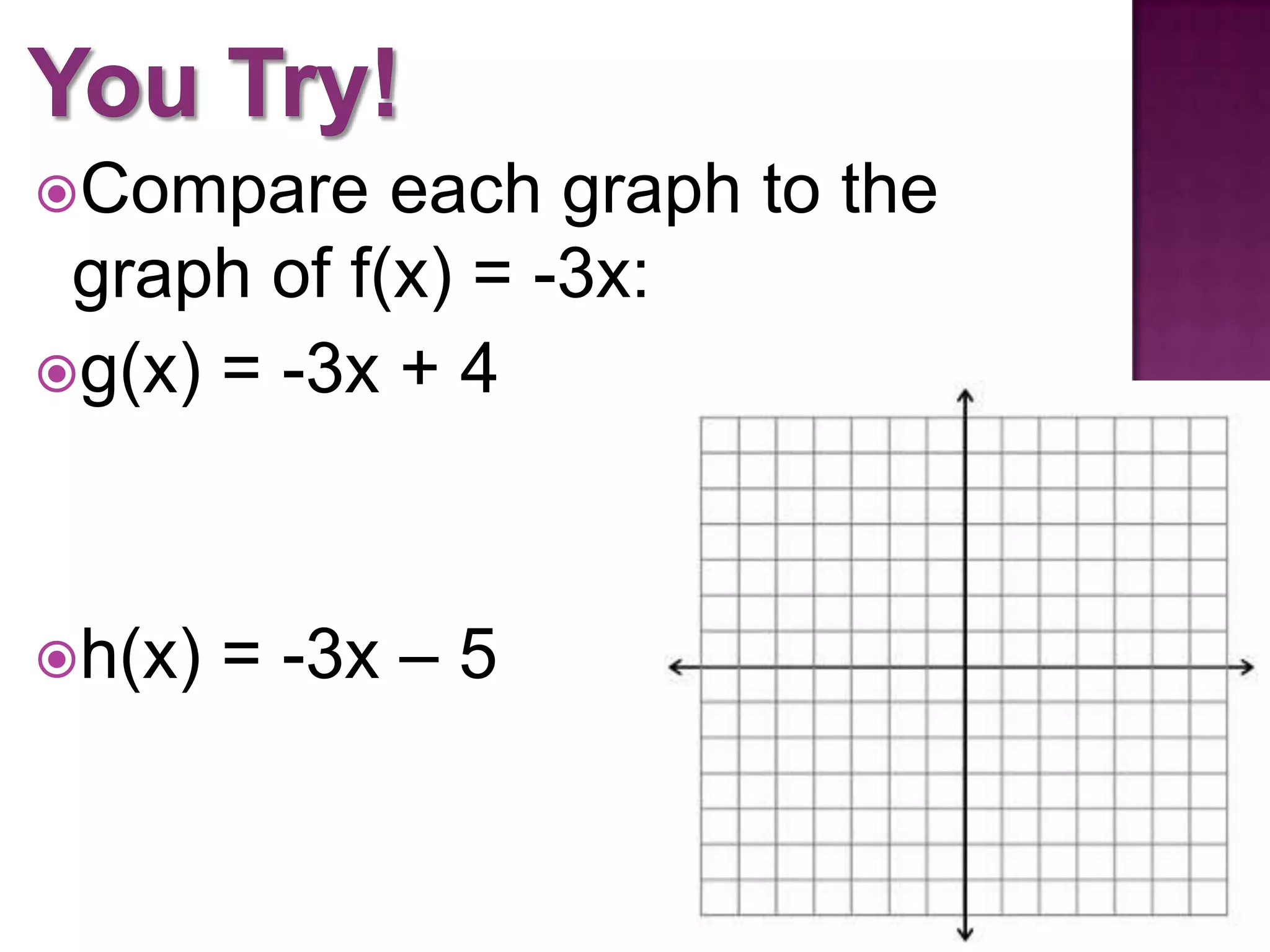
Graphing functions based on f(x) notation and understanding vertical translations and comparisons among different graphs.
















