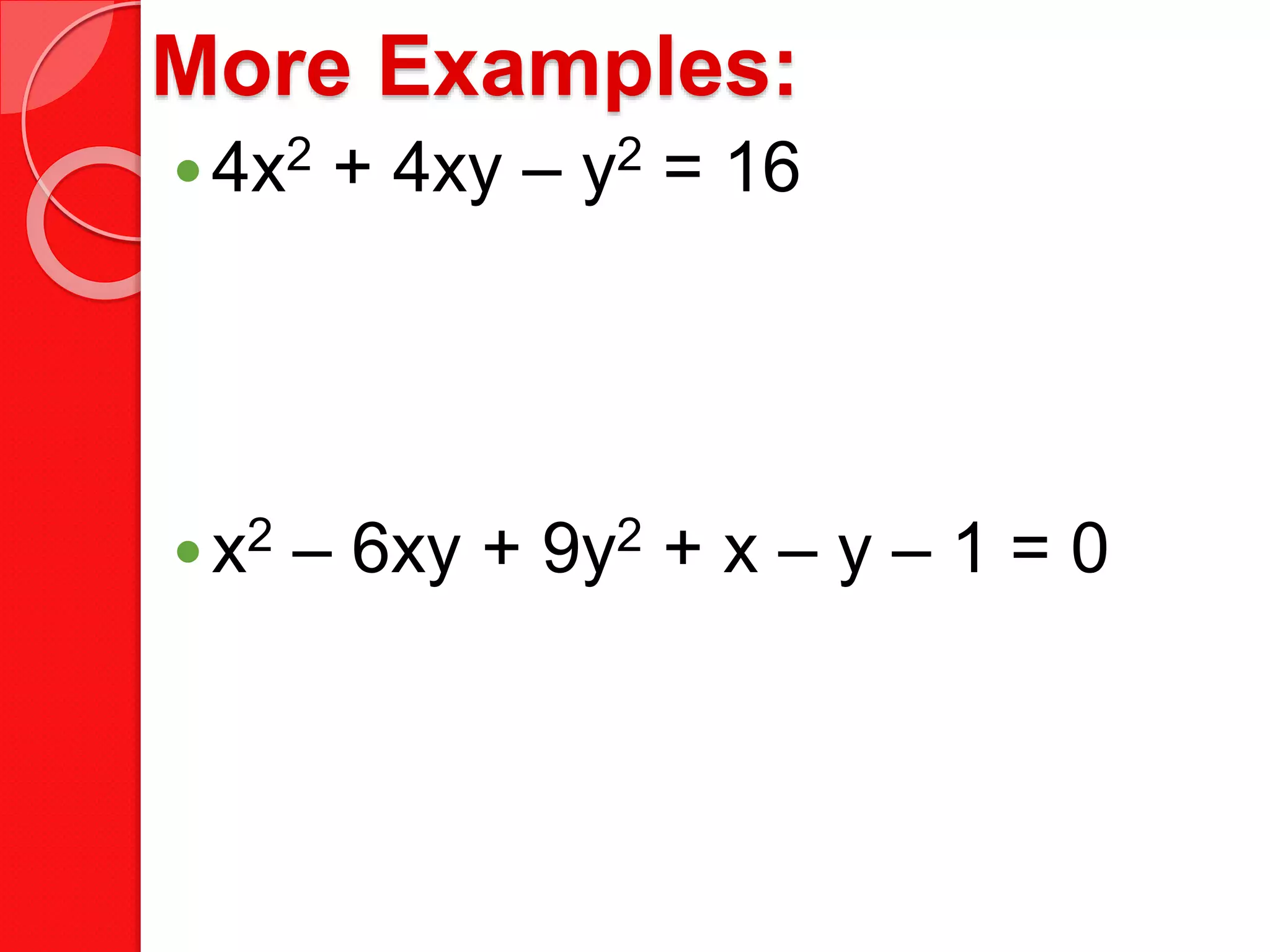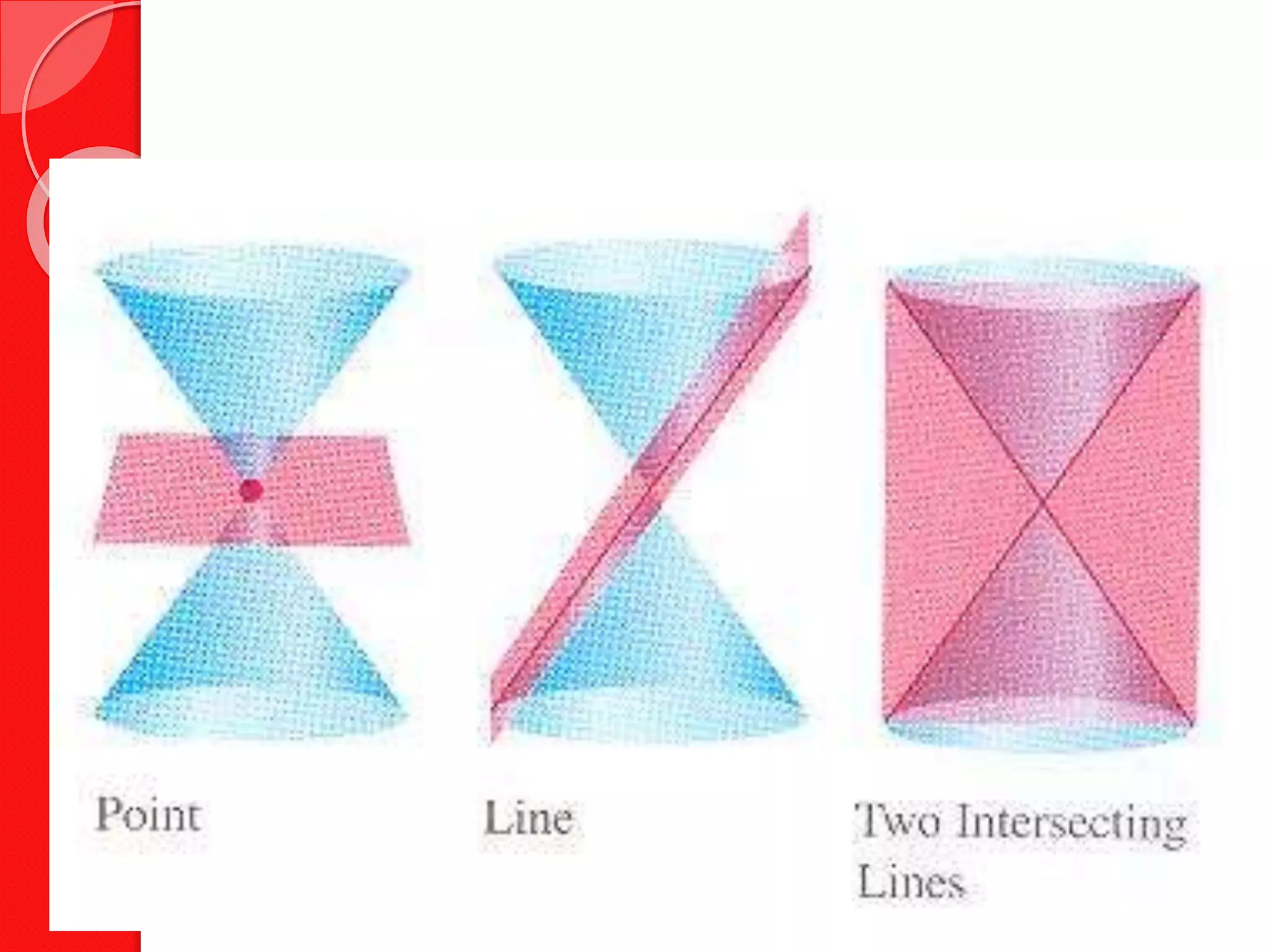
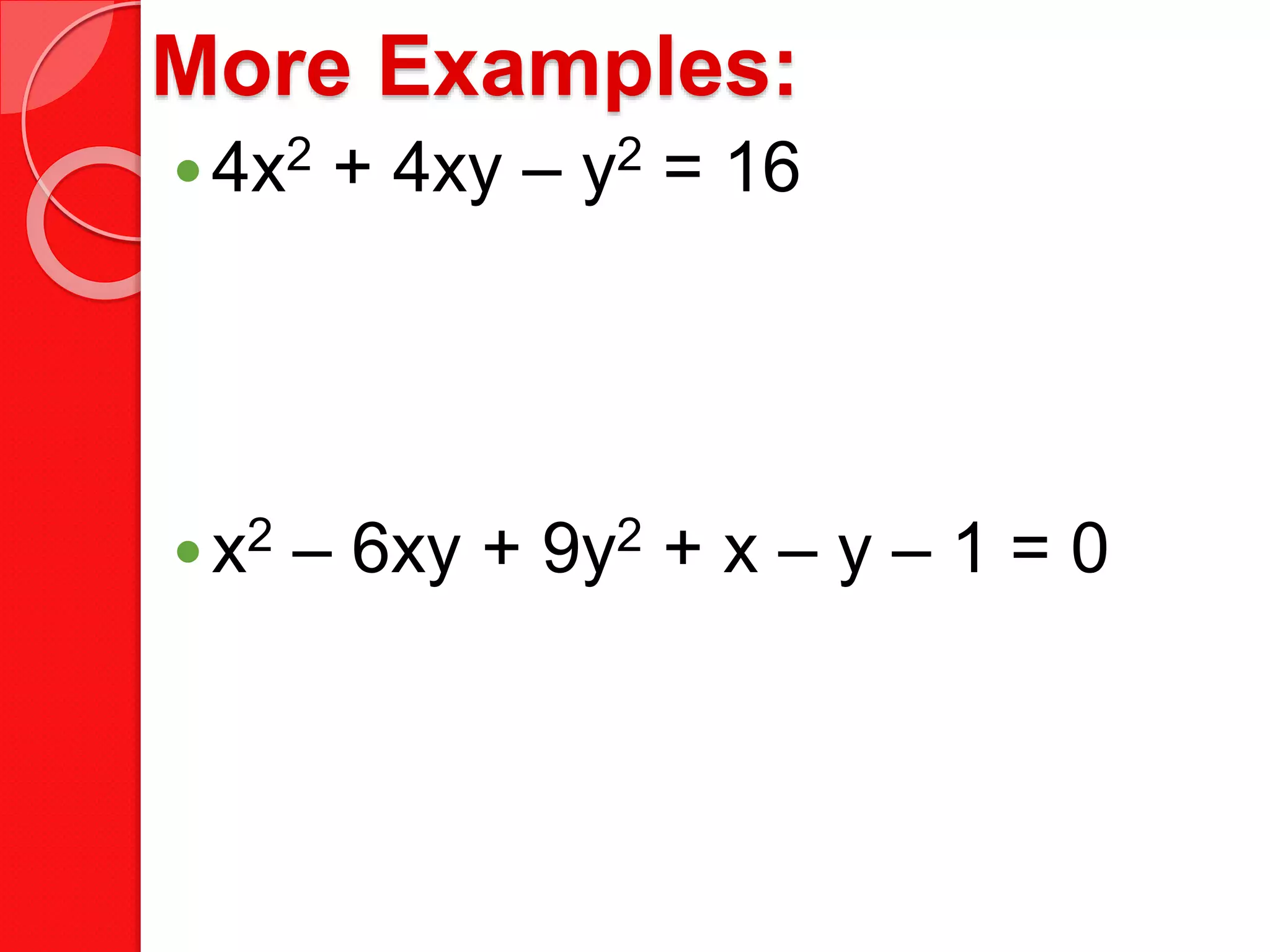
This document discusses classifying second-degree equations as different types of conic sections. It provides the general form of a second-degree equation, explains how to use the discriminant to determine if the graph is a circle, ellipse, parabola, or hyperbola, and gives examples of identifying the conic section from different equations. Key aspects covered include degenerate conics, the general form containing terms for x2, xy, y2, x, y, and the constant, and using the discriminant calculated from the equation coefficients to classify the conic section.

1. 6-7 A New Look at
Conic Sections
Objective:
Classify second-degree equations.

2. Degenerate Conics
Degenerate (adj.):
 having lost the physical, mental, or
moral qualities considered normal
and desirable; showing evidence of
decline.
 lacking some property, order, or
distinctness of structure previously
or usually present, in particular.

4. General Form
Ax2 + Bxy + Cy2 +Dx +Ey + F = 0
(where A, B, and C are not all 0)

5. The Discriminant
If B2 – 4AC is:
◦< 0 and A = C, B = 0  circle
◦< 0 and A ≠ C  ellipse
◦= 0  parabola
◦> 0  hyperbola
(As long as graph is not degenerate.)

6. Example:
Identify the graph of the
equation x2 – 2xy + 3y2 – 1 = 0

7. More Examples:
4x2 + 4xy – y2 = 16
x2 – 6xy + 9y2 + x – y – 1 = 0