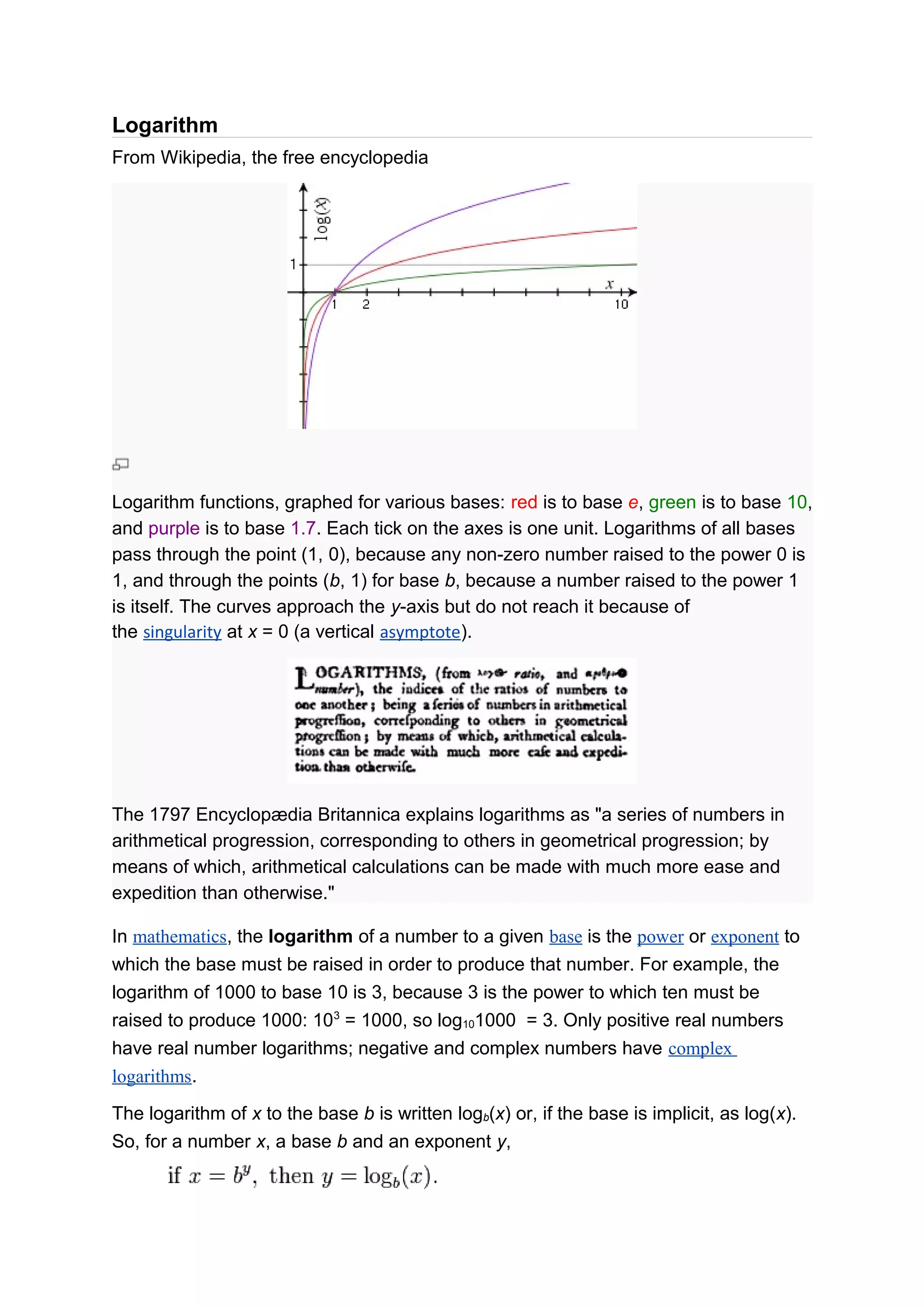
Logarithms are mathematical functions that represent the exponent to which a base must be raised to produce a given number. They simplify complex calculations by turning multiplication into addition and division into subtraction. Logarithms find applications across various fields such as statistics, physics, and computer science.

1. Logarithm
From Wikipedia, the free encyclopedia
Logarithm functions, graphed for various bases: red is to base e, green is to base 10,
and purple is to base 1.7. Each tick on the axes is one unit. Logarithms of all bases
pass through the point (1, 0), because any non-zero number raised to the power 0 is
1, and through the points (b, 1) for base b, because a number raised to the power 1
is itself. The curves approach the y-axis but do not reach it because of
the singularity at x = 0 (a vertical asymptote).
The 1797 Encyclopædia Britannica explains logarithms as "a series of numbers in
arithmetical progression, corresponding to others in geometrical progression; by
means of which, arithmetical calculations can be made with much more ease and
expedition than otherwise."
In mathematics, the logarithm of a number to a given base is the power or exponent to
which the base must be raised in order to produce that number. For example, the
logarithm of 1000 to base 10 is 3, because 3 is the power to which ten must be
raised to produce 1000: 103
= 1000, so log101000 = 3. Only positive real numbers
have real number logarithms; negative and complex numbers have complex
logarithms.
The logarithm of x to the base b is written logb(x) or, if the base is implicit, as log(x).
So, for a number x, a base b and an exponent y,

2. The bases used most often are 10 for the common logarithm, e for the natural
logarithm, and 2 for the binary logarithm.
An important feature of logarithms is that they reduce multiplication to addition, by
the formula:
That is, the logarithm of the product of two numbers is the sum of the logarithms of
those numbers.
Similarly, logarithms reduce division to subtraction by the formula:
That is, the logarithm of the quotient of two numbers is the difference between the
logarithms of those numbers.
The use of logarithms to facilitate complicated calculations was a significant
motivation in their original development. Logarithms have applications in fields as
diverse as statistics, chemistry, physics, astronomy, computer science, economics,
music, and engineering.
Logarithm of positive real numbers
[Definition
The graph of the function f(x) = 2x
(red) together with a depiction of log2
(3) ≈ 1.58.
The logarithm of a positive real number y with respect to another positive real
number b, where b is not equal to 1, is the real number x such that

3. That is, the x-th power of b must equal y.[1][2]
The logarithm x is denoted logb(y). (Some European countries write b
log(y) instead.
[3]
) The number b is referred to as the base. For b = 2, for example, this means
since 23
= 2 · 2 · 2 = 8. The logarithm may be negative, for example
since
The right image shows how to determine (approximately) the logarithm. Given the
graph (in red) of the function f(x) = 2x
, the logarithm log2(y) is the For any given
number y (y = 3 in the image), the logarithm of y to the base 2 is the x-coordinate of
the intersection point of the graph and the horizontal line intersecting the vertical
axis at 3.
Above, the logarithm has been defined to be the solution of an equation. For this to
be meaningful, it is thus necessary to ensure that there is always exactly one such
solution. This is done using three properties of the function f(x) = bx
: in the case b >
1, this function f(x) is strictly increasing, that is to say, f(x) increases when x does so.
Secondly, the function takes arbitrarily big values and arbitrarily small positive
values. Thirdly, the function is continuous. Intuitively, the function does not "jump": the
graph can be drawn without lifting the pen. These properties, together with
the intermediate value theorem ofelementary calculus ensure that there is indeed exactly
one solution x to the equation
f(x) = bx
= y,
for any given positive y. When 0 < b < 1, a similar argument is used, except that f(x)
= bx
is decreasing in that case.
[edit]Identities
Main article: Logarithmic Identities
The above definition of the logarithm implies a number of properties.
[edit]Logarithm of products
Logarithms map multiplication to addition. That is to say, for any two positive real
numbers x and y, and a given positive base b, the identity
logb(x · y) = logb(x) + logb(y).

4. For example,
log3(9 · 27) = log3(243) = 5,
since 35
= 243. On the other hand, the sum of log3(9) = 2 and log3(27) = 3 also
equals 5. In general, that identity is derived from the relation of powers and
multiplication:
bs
· bt
= bs + t.
Indeed, with the particular values s = logb(x) and t = logb(y), the preceding equality
implies
logb(bs
· bt
) = logb(bs + t
) = s + t = logb(bs
) + logb(bt
).
By virtue of this identity, logarithms make lengthy numerical operations easier to
perform by converting multiplications to additions. The manual computation process
is made easy by using tables of logarithms, or a slide rule. The property of common
logarithms pertinent to the use of log tables is that any decimal sequence of the same
digits, but different decimal-point positions, will have identical mantissas and differ
only in their characteristics.
Logarithm of powers
A related property is reduction of exponentiation to multiplication. Another way of
rephrasing the definition of the logarithm is to write
x = blog
b
(x)
.
Raising both sides of the equation to the p-th power (exponentiation) shows
xp
= (blog
b
(x)
)p
= bp · log
b
(x)
.
thus, by taking logarithms:
logb(xp
) = p logb(x).
In prose, the logarithm of the p-th power of x is p times the logarithm of x. As an
example,
log2(64) = log2(43
) = 3 · log2(4) = 3 · 2 = 6.
Besides reducing multiplication operations to addition, and exponentiation to
multiplication, logarithms reduce division to subtraction, and roots to division. For
example,