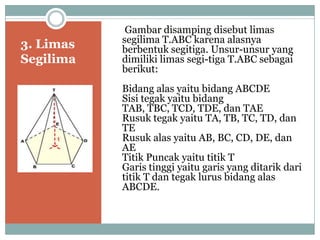
Dokumen ini membahas tentang prisma dan limas, termasuk pengertian, jenis-jenis, serta rumus untuk menghitung volume dan luas permukaan. Prisma diklasifikasikan berdasarkan bentuk alasnya seperti segitiga, segiempat, dan lainnya, sedangkan limas juga memiliki jenis berdasarkan bentuk alas. Contoh soal disertakan untuk mengilustrasikan cara perhitungan volume dan luas permukaan pada prisma dan limas.

1. K E L O M P O K :
1 . D E A N D R E S U G I A N T O ( 8 )
2 . D I O S U S E N O W O N G S O ( 1 0 )
3 . G R A C E L L A P A T R I C I A ( 1 6 )
4 . S A N N I A J U W I C A ( 2 7 )
5 . S H E L L Y N H A R T O N O ( 2 9 )
TUGAS MATEMATIKA

2. Prisma
Pengertian Prisma
Suatu bangun ruang yang bentuk dan ukuran sisi atas dengan sisi
bawah sama serta rusuk-rusuk tegak yang sejajar disebut prisma.
Sebuah bangun prisma ditentukan oleh bentuk alasnya. Maksudnya
bahwa penamaan suatu prisma berdasarkan bentuk alasnya,
contohnya, suatu bangun prisma yang alasnya berbentuk segitiga
maka dinamakan prisma segitiga, prisma yang alasnya berbentuk
segiempat maka dinamakan prisma segiempat, prisma yang
alasnya berbentuk segi-lima maka dinamakan prisma segi-lima, dan
seterunya.
Jenis-Jenis Prisma
Seperti yang dijelaskan di atas bahwa penamaan prisma detentukan
oleh bentuk alasnya maka prisma ada banyak jenis. Berikut adalah
beberapa diantaranya:

4. 1. Prisma Segitiga
 Memiliki 5 sisi
 Memiliki 6 titik sudut
 Memiliki 9 rusuk
 Memiliki 6 diagonal sisi

5. 2. Prisma segiempat
 Memiliki 6 sisi
 Memiliki 8 titik sudut
 Memiliki 12 rusuk
 Memiliki 12 diagonal sisi

6. 3. Prisma Segilima
 Memiliki 7 sisi
 Memiliki 10 titik sudut
 Memiliki 15 rusuk
 Memiliki 20 diagonal sisi

7. 4. Prisma segienam
 Memiliki 8 sisi
 Memiliki 18 rusuk
 Memiliki 12 titik sudut

8. 5. Prisma Segi n
 Banyak sisi = n+2
 Banyak rusuk = n x 3
 Banyak titik sudut = n x 2

9. Rumus-Rumus Limas
1. Volume Limas
Untuk mencari besar volume limas digunakan rumus:
Volume Limas = 1/3 x Luas Alas x t
2. Luas Permukaan
Untuk mencari luas permukaan limas digunakan rumus:
L= Jumlah Luas bidang-bidang sisinya.
Contoh Soal Limas
1/. Suatu limas segiempat alasnya berbentuk persegi dan volumenya 1.350 cm3. Apabila tinggi
limas tersebut 18 cm, tentukan panjang sisi alasnya?
Penyelesaian
Dik : V = 1.350 cm3 dan tinggi = 18 cm
V = 1/3 x L x t
1.350 = 1/3 L. 18
1350 = 6 L

10. Contoh Soal prisma
1. Sebuah prisma segitiga tegak alasnya berbentuk segitiga siku-siku, dengan panjang rusuk alasnya 4 cm,
3 cm, 5 cm dengan tinggi prisma 10 cm. Hitunglah:
a. Volume prisma
b. Luas permukaan prisma
Penyelesaian
Luas segitiga = ½ x alas x tinggi
= ½ x 4 cm x 3 cm
= ½ x 12 cm2
= 6 cm2
Luas selubung prisma = [(4 x 10) + (5 x 10) + (3 x 10)]
= (40 + 50 + 30) cm2
= 120 cm2
1. Volume Prisma Segitiga = Luas alas x tinggi
= 6 cm2 x 10 cm
= 60 cm3
2. Luas permukaan prisma
= Luas alas + luas atas + luas selubungnya
= 6 cm2 + 6 cm2 + 120 cm2
= 132 cm2
2.Suatu bangun prisma segitiga terbuat dari karton, alasnya berbentuk segitiga siku-siku dengan sisi siku-
siku 3 cm dan 4 cm. Apabila tinggi prisma 5 cm, berapa luas karton yang diperlukan?
Penyelesaian
BC2 = 32 + 42
= 9 + 15 = 25
BC = 25 = 5 cm
Luas sisi Alas ABC = Luas sisi Atas DEF = ½ x 3 x 4 = 6 cm2
Luas selubung ABED = 4 cm x 5 cm = 20 cm2
Luas selubung ACFD = 3 cm x 5 cm = 15 cm2
Luas selubung BCFE = 5 cm x 5 cm = 25 cm2
Jadi, luas karton yang diperlukan (luas sisi prisma)
= 6 cm2 + 6 cm2 + 20 cm2 + 15 cm2 + 25 cm2 = 72 cm2

11. Limas
Limas adalah bangun ruang yang dibatasi oleh
sebuah segi-n dan beberapa segitiga yang alasnya
berimpit dengan segi-n tersebut dan bertemu pada
satu titik di luar bidang alas.
Jenis-jenis Limas
Jenis Limas ada 4 berdasarkan bentuk alasnya.

12. 1. Limas
Segitiga
Gambar di samping disebut limas
segitiga T.ABC karena alasnya
berbentuk segitiga. Unsur-unsur yang
dimiliki limas segi-tiga T.ABC sebagai
berikut:
Bidang alas yaitu bidang ABC
Sisi tegak yaitu bidang TAB, TBC,dan
TAC
Rusuk tegak yaitu TA, TB, dan TC
Rusuk alas yaitu AB, BC, dan AC
Titik Puncak yaitu titik T
Garis tinggi yaitu garis yang ditarik dari
titik T dan tegak lurus bidang alas ABC.

13. 2. Limas
Segiempat
Gambar di samping disebut limas
segiempat T.ABCD karena alasnya
berbentuk segiempat. Unsur-unsur
yang dimiliki limas segiempat T.ABCD
sebagai berikut:
Bidang alas yaitu bidang ABCD
Sisi tegak yaitu bidang
TAB, TBC, TCD, dan TAD
Rusuk tegak yaitu TA, TB, TC, dan TD
Rusuk alas yaitu AB, BC, CD, dan DA
Titik Puncak yaitu titik T
Garis tinggi yaitu garis yang ditarik dari
titik T dan tegak lurus bidang alas
ABCD.

14. 3. Limas
Segilima
Gambar disamping disebut limas
segilima T.ABC karena alasnya
berbentuk segitiga. Unsur-unsur yang
dimiliki limas segi-tiga T.ABC sebagai
berikut:
Bidang alas yaitu bidang ABCDE
Sisi tegak yaitu bidang
TAB, TBC, TCD, TDE, dan TAE
Rusuk tegak yaitu TA, TB, TC, TD, dan
TE
Rusuk alas yaitu AB, BC, CD, DE, dan
AE
Titik Puncak yaitu titik T
Garis tinggi yaitu garis yang ditarik dari
titik T dan tegak lurus bidang alas
ABCDE.

15. Limas Segi-n
Untuk limas segi-n memiliki unsur-unsur yaitu
Bidang sisi = n + 1
Titik sudut = n + 1
Rusuk = 2 n