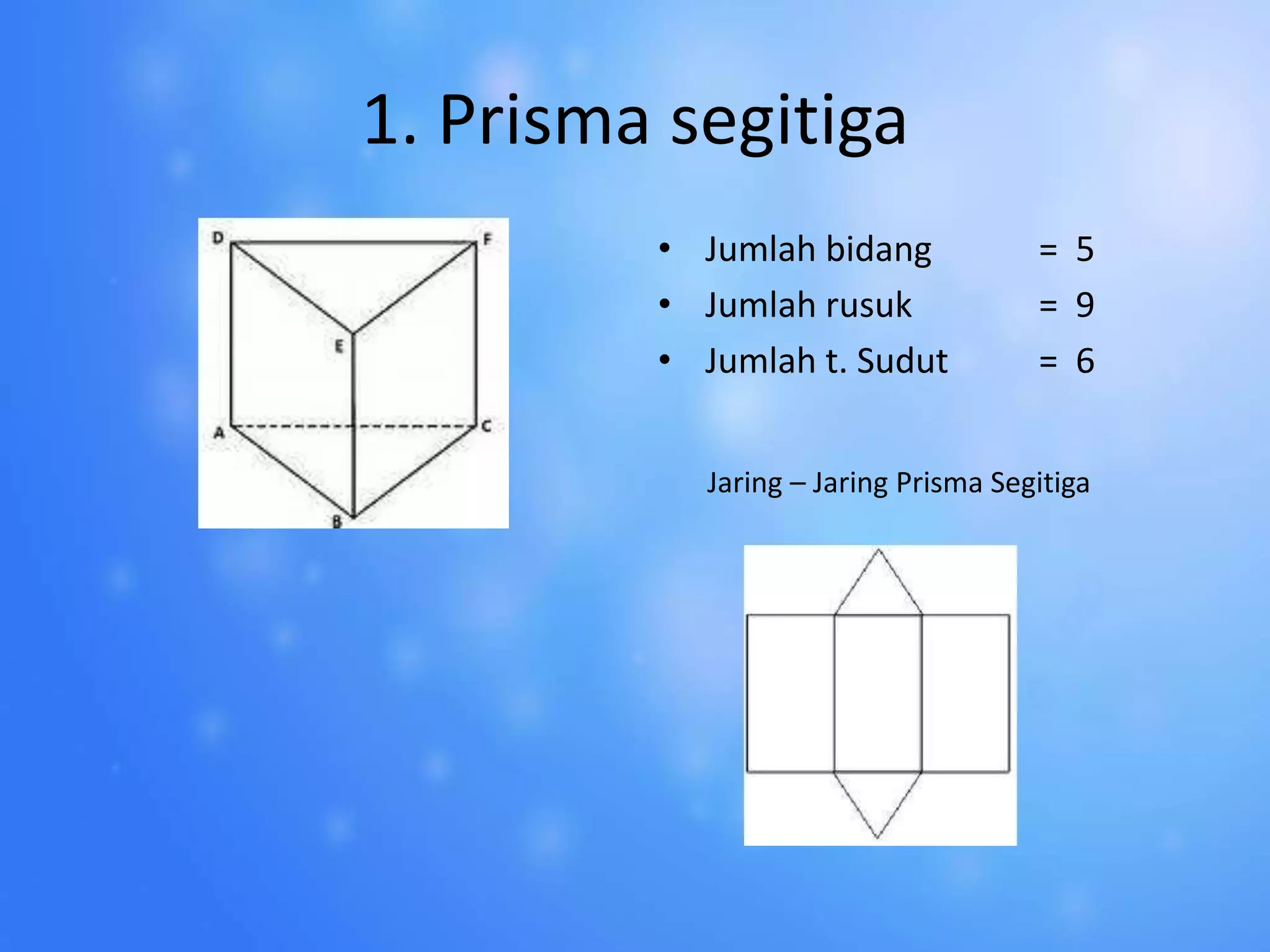
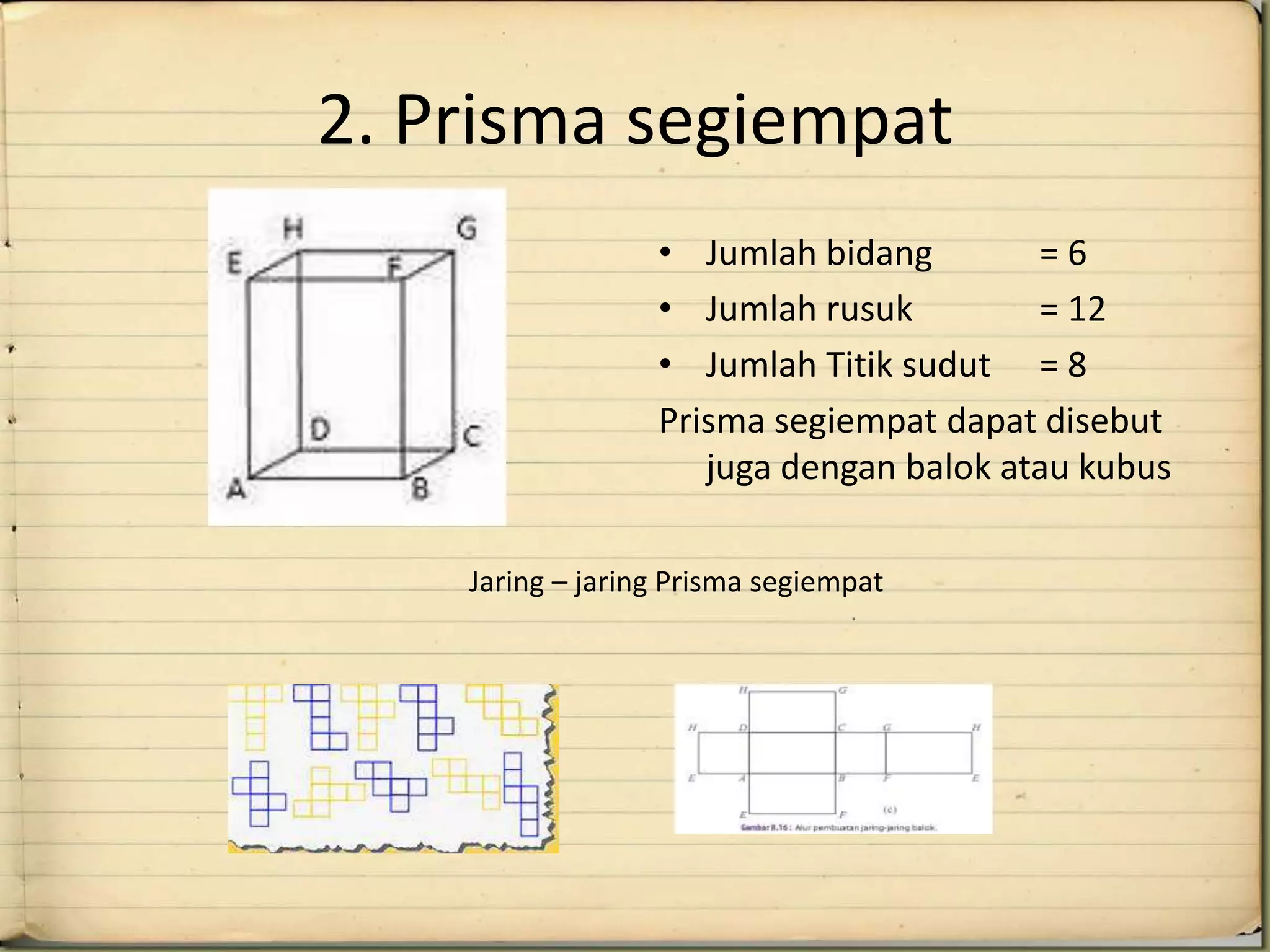
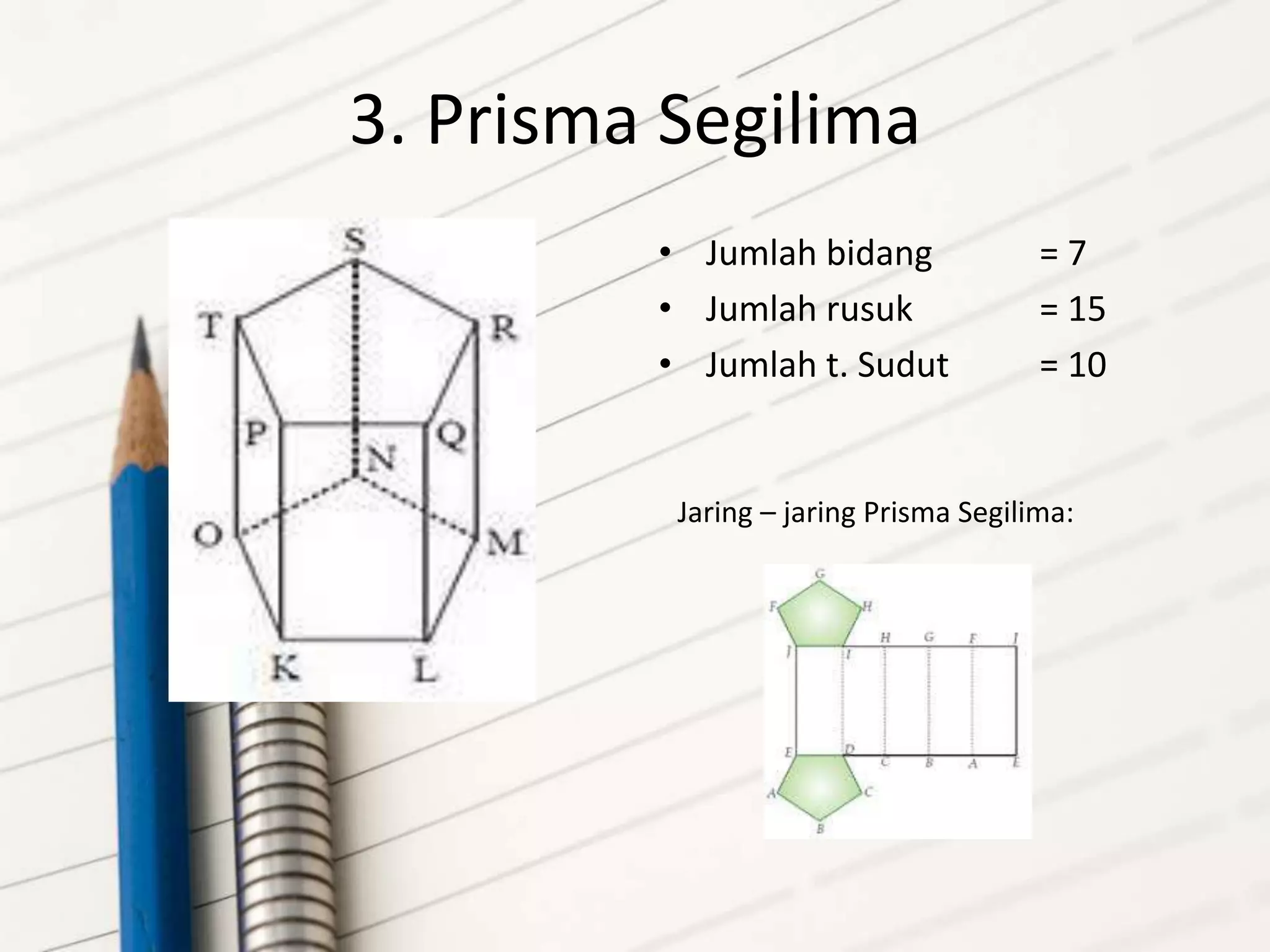
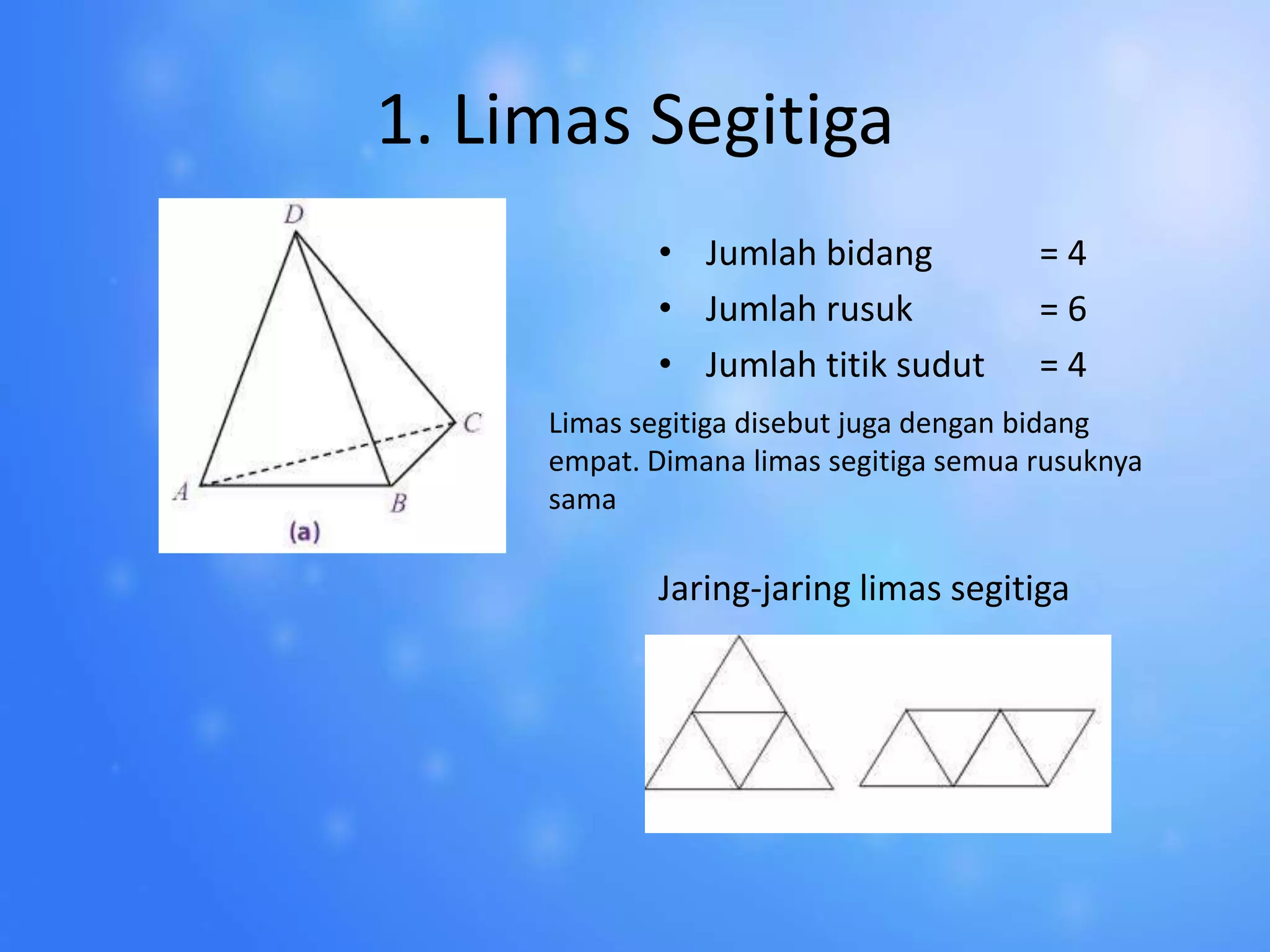
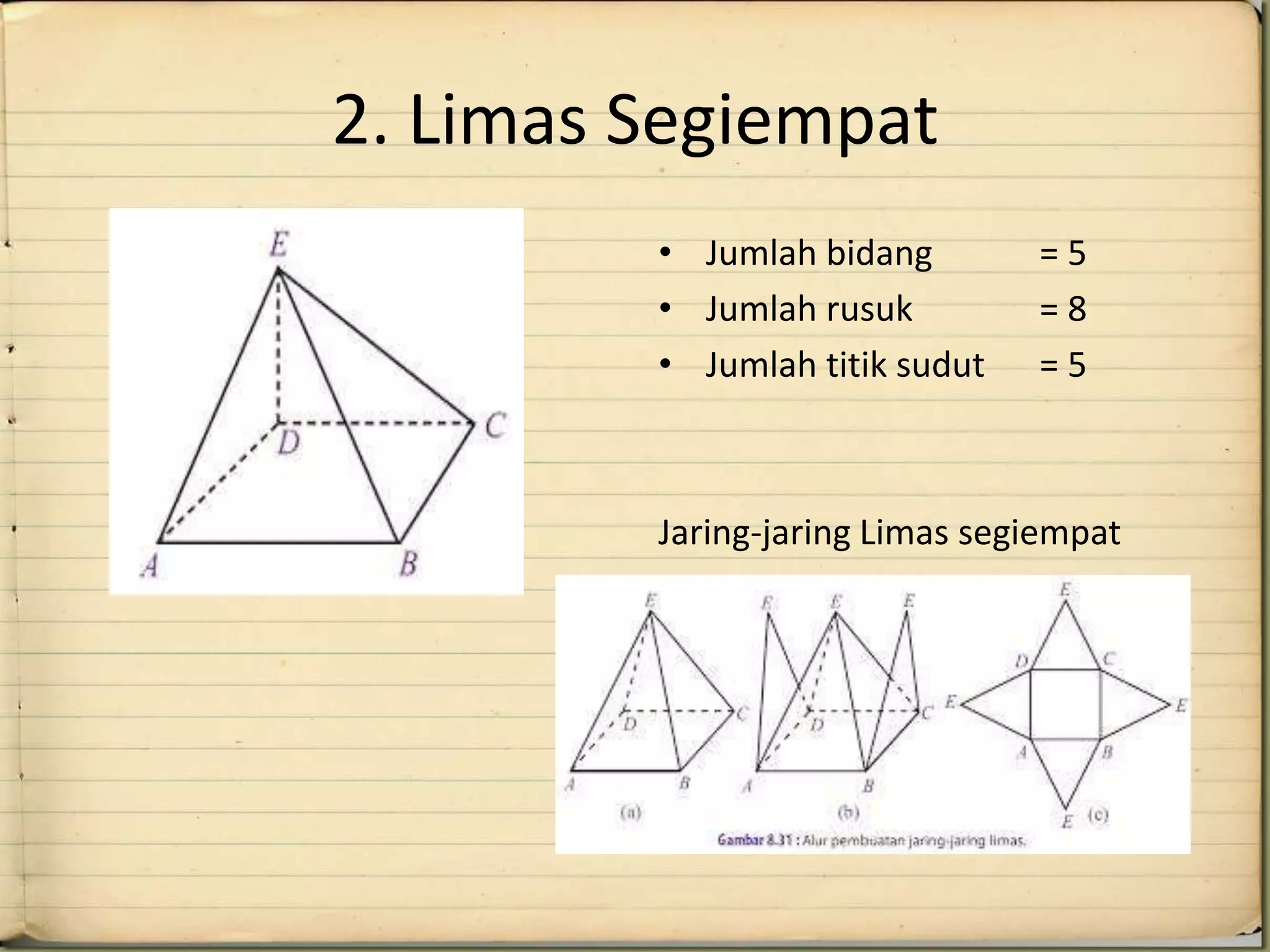
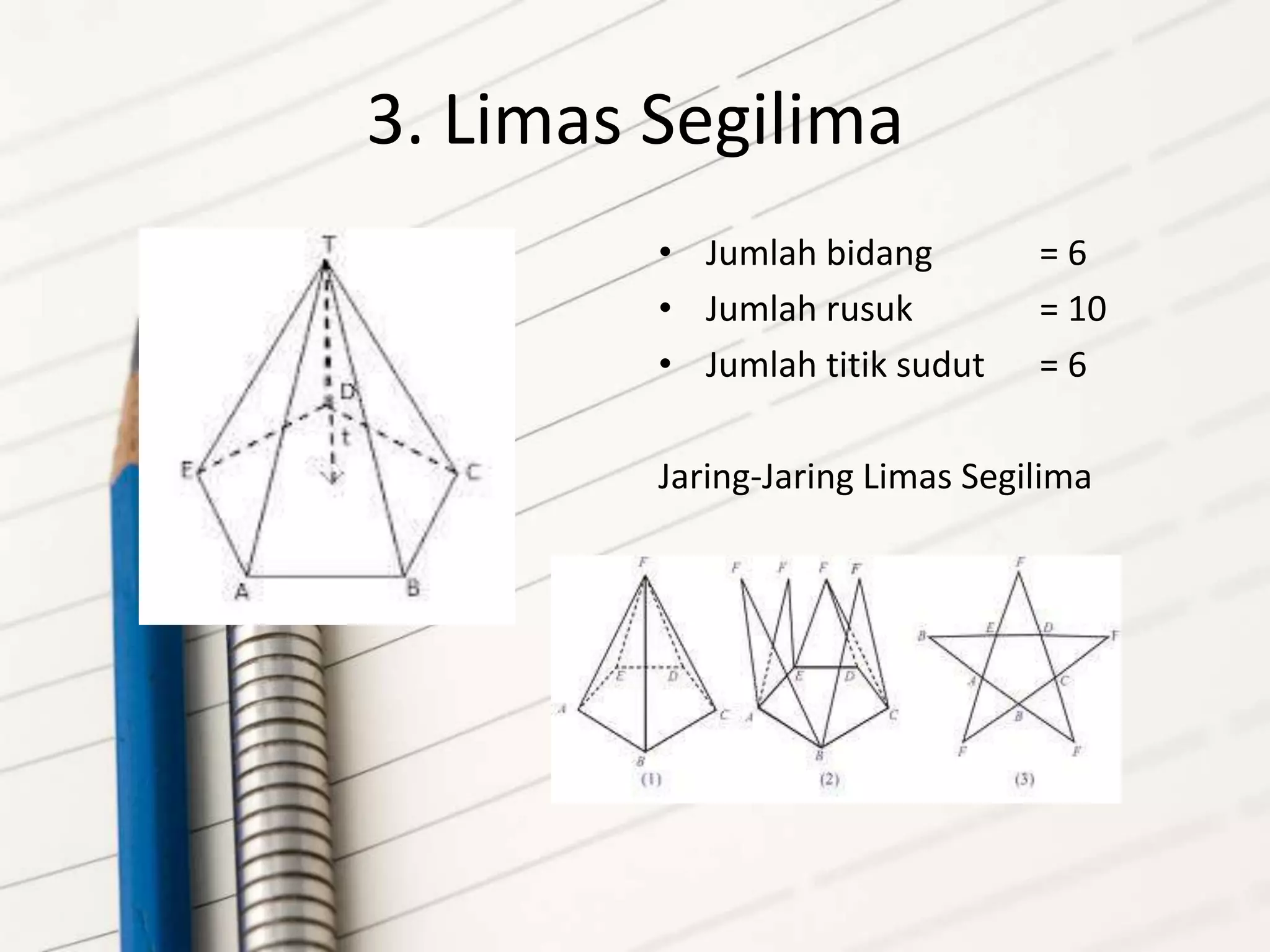
Dokumen tersebut membahas tentang prisma dan limas, termasuk definisi, contoh, rumus, dan jaring-jaringnya. Prisma dijelaskan sebagai bangun ruang yang dibatasi oleh dua bidang sejajar, sedangkan limas dibatasi oleh satu alas dan sisi tegak berbentuk segitiga. Diberikan pula contoh prisma segitiga, segiempat, dan segilima serta limas yang sama.

1. Tugas Matematika
Prisma & Limas
Kelompok:
-Karen Ng (23)
-Kelnia Mellenia (24)
-Sherin Agustina (44)

2. Prisma
• Prisma adalah bangun ruang yang dibatasi oleh 2 buah bidang,
berbentuk segi banyak yang sejajar dan sisi-sisi tegak yang
berpotongan menurut rusuk-rusuk yang sejajar
• Sifat-sifat prisma adalah sebagai berikut :
– Prisma memiliki bentuk alas dan atap yang kongruen.
Pada gambar terlihat bahwa segitiga ABC dan DEF memiliki ukuran dan
bentuk yang sama.
– Setiap sisi bagian samping prisma berbentuk persegipanjang. Prisma
segitiga pada gambar dibatasi oleh tiga persegipanjang di setiap sisi
sampingnya, yaitu ABED, BCFE, dan ACFD.
– Prisma memiliki rusuk tegak.

3. • Contoh - contoh Prisma:
1. Prisma segitiga
2. Prisma segiempat
3. Prisma segilima,dll
• Rumus :
Prisma Segi-n :
– Jumlah titik sudut : 2n
– Jumlah bidang : n+2
– Jumlah rusuk : 3n
– Jumlah diagonal bidang : n(n-1)
– Jumlah diagonal ruang : n(n-3)
– Volume : Luas alas x tinggi
– Luas permukaan : (2 x luas alas) + jumlah luas sisi tegak

4. 1. Prisma segitiga
• Jumlah bidang = 5
• Jumlah rusuk = 9
• Jumlah t. Sudut = 6
Jaring – Jaring Prisma Segitiga

5. 2. Prisma segiempat
• Jumlah bidang = 6
• Jumlah rusuk = 12
• Jumlah Titik sudut = 8
Prisma segiempat dapat disebut
juga dengan balok atau kubus
Jaring – jaring Prisma segiempat

6. 3. Prisma Segilima
• Jumlah bidang = 7
• Jumlah rusuk = 15
• Jumlah t. Sudut = 10
Jaring – jaring Prisma Segilima:

7. Limas
• Limas adalah bangun ruang yang dibatasi oleh alas berbentuk segi –n yang
kemudian dari sisi alas tersebut dibentuk sisi tegak berbentuk segitiga yang
bertemu pada satu titik puncak.
• Limas beraturan adalah limas yang alasnya berupa segi n beraturan dan
proyeksi titik puncak pada alas berimpit dengan titik pusat alas.
Contoh-contoh limas :
- Limas segitiga
- Limas segiempat
- Limas segilima
- dll

8. Rumus
Limas Segi – n
- Jumlah titik sudut = n+1
- Jumlah bidang = n+1
- Jumlah rusuk = 2n
- Jumlah diagonal bidang = n-3
- Tidak memiliki diagonal ruang
- Volume = ⅓ x luas alas x tinggi
- Luas Permukaan = Luas alas + jumlah luas sisi tegak

9. 1. Limas Segitiga
• Jumlah bidang = 4
• Jumlah rusuk = 6
• Jumlah titik sudut = 4
Jaring-jaring limas segitiga
Limas segitiga disebut juga dengan bidang
empat. Dimana limas segitiga semua rusuknya
sama

10. 2. Limas Segiempat
• Jumlah bidang = 5
• Jumlah rusuk = 8
• Jumlah titik sudut = 5
Jaring-jaring Limas segiempat

11. 3. Limas Segilima
• Jumlah bidang = 6
• Jumlah rusuk = 10
• Jumlah titik sudut = 6
Jaring-Jaring Limas Segilima