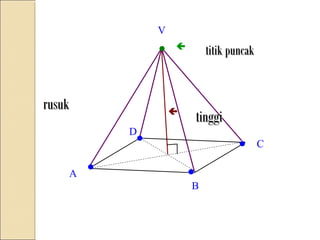
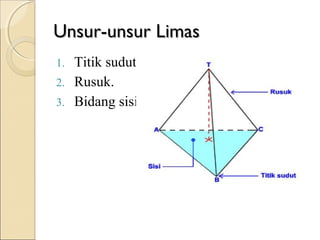
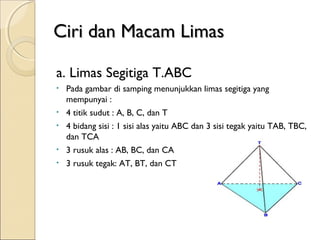
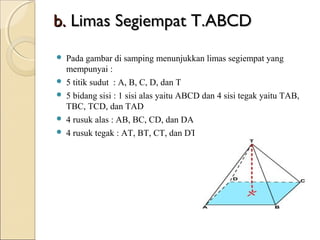
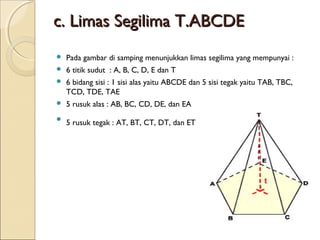
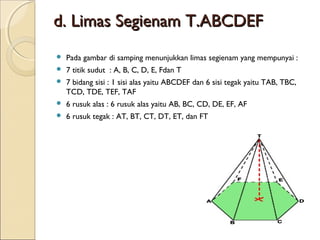
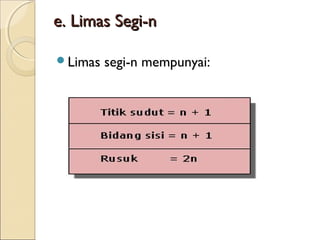
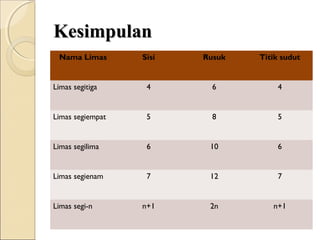
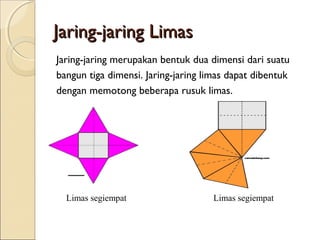
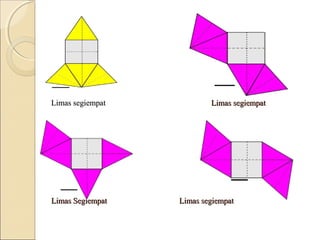
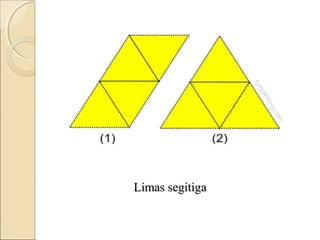
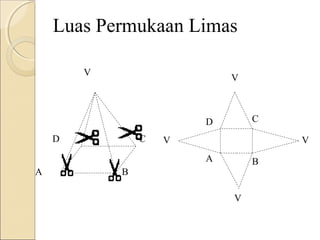
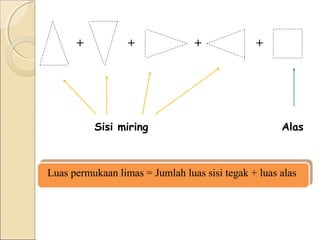
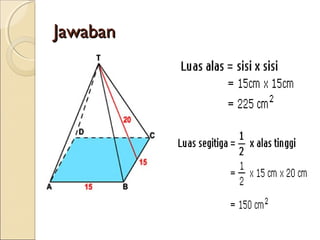
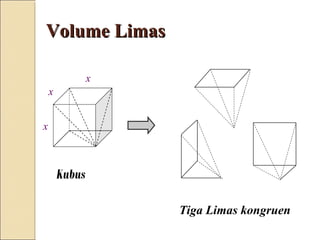
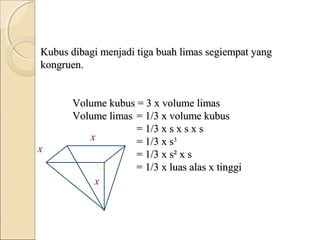
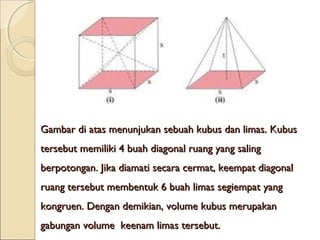
Dokumen ini membahas tentang limas, termasuk definisi, sifat, ciri-ciri, dan macam-macam limas seperti limas segitiga, segiempat, segilima, dan segienam. Juga dijelaskan mengenai jaring-jaring limas, luas permukaan, dan volume limas dengan contoh soal perhitungan. Secara umum, volume limas dihitung sebagai 1/3 kali luas alas dikali tinggi.

1. 1.
2.
3.
4.
5.
Bastian Anggit Sulistyo
Oktarina Indrawati
Azizah Niken Mawar
Nunung Setyadi
Bayu Dwi Santosa
12144600006
12144600010
12144600018
12144600025
12144600034
LIMAS

2. DEFINISI LIMAS
Limas adalah suatu
bangun ruang yang
dibatasi oleh sebuah
segibanyak (segi-n)
dan segitiga-segitiga
yang mempunyai titik
puncak persekutuan di
luar bidang
segibanyak itu.

3. V
titik puncak
 
rusuk

D
tinggi

A



B
C

4. Unsur-unsur Limas
Titik sudut.
2. Rusuk.
3. Bidang sisi.
1.

5. Sifat-sifat Limas
Bidang atas berupa sebuah titik (lancip).
2. Bidang bawah berupa bangun datar.
3. Bidang sisi tegak berupa segitiga.
4. Limas mempunyai diagonal bidang dan
tidak mempunyai diagonal ruang.
1.

6. Ciri dan Macam Limas
a. Limas Segitiga T.ABC
•
•
•
•
•
Pada gambar di samping menunjukkan limas segitiga yang
mempunyai :
4 titik sudut : A, B, C, dan T
4 bidang sisi : 1 sisi alas yaitu ABC dan 3 sisi tegak yaitu TAB, TBC,
dan TCA
3 rusuk alas : AB, BC, dan CA
3 rusuk tegak: AT, BT, dan CT

7. b. Limas Segiempat T.ABCD





Pada gambar di samping menunjukkan limas segiempat yang
mempunyai :
5 titik sudut : A, B, C, D, dan T
5 bidang sisi : 1 sisi alas yaitu ABCD dan 4 sisi tegak yaitu TAB,
TBC, TCD, dan TAD
4 rusuk alas : AB, BC, CD, dan DA
4 rusuk tegak : AT, BT, CT, dan DT

8. c. Limas Segilima T.ABCDE

Pada gambar di samping menunjukkan limas segilima yang mempunyai :

6 titik sudut : A, B, C, D, E dan T

6 bidang sisi : 1 sisi alas yaitu ABCDE dan 5 sisi tegak yaitu TAB, TBC,
TCD, TDE, TAE

5 rusuk alas : AB, BC, CD, DE, dan EA

5 rusuk tegak : AT, BT, CT, DT, dan ET

9. d. Limas Segienam T.ABCDEF

Pada gambar di samping menunjukkan limas segienam yang mempunyai :

7 titik sudut : A, B, C, D, E, Fdan T

7 bidang sisi : 1 sisi alas yaitu ABCDEF dan 6 sisi tegak yaitu TAB, TBC,
TCD, TDE, TEF, TAF

6 rusuk alas : 6 rusuk alas yaitu AB, BC, CD, DE, EF, AF

6 rusuk tegak : AT, BT, CT, DT, ET, dan FT

10. e. Limas Segi-n
Limas
segi-n mempunyai:

11. Kesimpulan
Nama Limas
Sisi
Rusuk
Titik sudut
Limas segitiga
4
6
4
Limas segiempat
5
8
5
Limas segilima
6
10
6
Limas segienam
7
12
7
n+1
2n
n+1
Limas segi-n

12. Jaring-jaring Limas
Jaring-jaring merupakan bentuk dua dimensi dari suatu
bangun tiga dimensi. Jaring-jaring limas dapat dibentuk
dengan memotong beberapa rusuk limas.
Limas segiempat
Limas segiempat

13. Limas segiempat
Limas Segiempat
Limas segiempat
Limas segiempat

14. Limas segitiga

15. Luas Permukaan Limas
V
V
C
D
D
C
V
V
A
A
B
B
V

16. +
+
Sisi miring
+
+
Alas
Luas permukaan limas = Jumlah luas sisi tegak + luas alas
Luas permukaan limas = Jumlah luas sisi tegak + luas alas

17. Contoh Soal
Sebuah limas segi empat beraturan, rusuk
rusuk alasnya 15 cm dan jarak dari puncak
ke rusuk alas 20 cm. Tentukan luas sisi
limas !

18. Jawaban

19. Luas limas = jumlah luas sisi tegak + luas alas
Luas limas = (4 x 150 cm²) + 225 cm²
= 600 cm² + 225 cm²
= 825 cm²
Jadi luas sisi limas 825 cm².
http://mediapemb.blogspot.com

20. Volume Limas
Volume atau bisa juga disebut
kapasitas
adalah penghitungan seberapa banyak
ruang yang bisa ditempati dalam suatu
objek.
Volume limas dapat ditentukan dengan
membelah sebuah kubus menjadi tiga atau
enam buah limas yang kongruen.

21. Volume Limas
x
x
x
Kubus
Tiga Limas kongruen

22. Kubus dibagi menjadi tiga buah limas segiempat yang
kongruen.
x
Volume kubus = 3 x volume limas
Volume limas = 1/3 x volume kubus
= 1/3 x s x s x s
x
= 1/3 x s3
= 1/3 x s² x s
= 1/3 x luas alas x tinggi
x

23. Gambar di atas menunjukan sebuah kubus dan limas. Kubus
tersebut memiliki 4 buah diagonal ruang yang saling
berpotongan. Jika diamati secara cermat, keempat diagonal
ruang tersebut membentuk 6 buah limas segiempat yang
kongruen. Dengan demikian, volume kubus merupakan
gabungan volume keenam limas tersebut.

25. 6 x volume limas = volume kubus
Volume limas
= 1/6 x s x s x s
= 1/6 x s 2 x s
= 1/6 x s2 x 2s/2
= 2/6 x s2 x s/2
= 1/3 x s2 x s/2
Oleh karena s2 merupakan luas alas kubus dan s/2
merupakan tinggi limas maka,
Volume limas
= 1/3 x s2 x s/2
= 1/3 x luas alas limas x tinggi limas

26. Kesimpulan
Volume limas = 1/3 x Luas alas x Tinggi
Volume limas = 1/3 x Luas alas x Tinggi

27. Contoh soal
Hitunglah volume limas yang mempunyai
tinggi 30 cm dan luas alas 100 cm² !

28. Jawaban