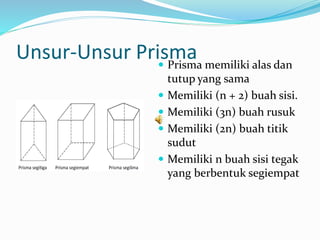
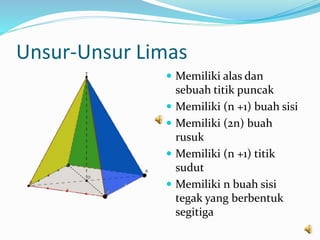
Dokumen ini menjelaskan tentang prisma dan limas, termasuk definisi, unsur-unsur, rumus luas permukaan, dan volume masing-masing bangun ruang. Contoh soal dengan penyelesaian juga disertakan untuk mengilustrasikan cara menghitung luas permukaan dan volume. Ringkasan mencakup berbagai jenis prisma dan limas serta rumus-rumus yang diperlukan untuk perhitungan tersebut.

1. DISUSUN OLEH HARUM, S.Pd
APRIL 2020
Disusun Oleh
HARUM, S.Pd

2. PRISMA
 Prisma adalah bangun
ruang yang
mempunyai bidang
alas dan bidang atas
sejajar serta kongruen.
Prisma diberi nama
sesuai dengan bidang
alasnya. Bila alasnya
berbentuk segitiga
maka disebut prisma
segitiga dst.

3. Unsur-Unsur Prisma Prisma memiliki alas dan
tutup yang sama
 Memiliki (n + 2) buah sisi.
 Memiliki (3n) buah rusuk
 Memiliki (2n) buah titik
sudut
 Memiliki n buah sisi tegak
yang berbentuk segiempat

4. LUAS PERMUKAAN DAN VOLUME
PRISMA
 PRISMA: Luas
permukaan prisma dapat
dihitung dengan jaring-
jaring prisma. Caranya
adalah dengan
menjumlahkan semua
luas bangun datar pada
jaring-jaring prisma.

5. Volume Prisma

6. LIMAS
Limas adalah suatu bangun ruang yang dibatasi oleh sebuah
segi banyak (segi n) dan segitiga-segitiga yang mempunyai
titik puncak persekutuan di luar bidang segibanyak itu.

7. Unsur-Unsur Limas
 Memiliki alas dan
sebuah titik puncak
 Memiliki (n +1) buah sisi
 Memiliki (2n) buah
rusuk
 Memiliki (n +1) titik
sudut
 Memiliki n buah sisi
tegak yang berbentuk
segitiga

8. Luas Permukaan Limas
 Luas permukaan limas
dapat dihitung dengan
jaring-jaring limas.
Caranya adalah dengan
menjumlahkan semua
luas bangun datar pada
jaring-jaring limas. Luas
limas = luas segiempat
ABCD + 4 kali luas
segitiga jaring2 limas.

9. Jadi luas permukaan limas adalah

10. VOLUME LIMAS  Dari gambar di atas, terdapat 6 bangun Limas,
yaitu Limas T.ABCD, Limas T.BCGF, Limas
T.CDHG, Limas T.ADHE, Limas T.ABFE, dan
Limas T.EFGH. Limas-limas tersebut memiliki
bentuk alas yang sama, yaitu berbentuk
persegi dengan panjang sisinya adalah serta
meliki tinggi yang sama pula, yaitu . Oleh
karena itu, dapat disimpulkan bahwa
 6 x Volume Limas = Volume Kubus
= s3
= s2 x s
Volume Limas = 1/6 x s2 x s
= 1/6 x s2 x 2t
= 1/3 x s2 x t
Karena alasnya berbentuk persegi dan luas persegi
= s x s, berakibat
= 1/3 x s2 x t
 Jadi, Rumus Volume Limas adalah
V limas = 1/3 x luas alas x tinggi

11. CONTOH SOAL
1. Sebuah prisma alasnya
berbentuk segitiga siku-siku
dengan panjang sisi 8 cm, 10
cm serta 12 cm dan tinggi
prisma tersebut adalah 15 cm.
Tanpa menggambar prisma
tersebut dahulu, tentukan
luas permukaan prisma?
 Pembahasan :
 Diketahui :
 sisi segitiga : 8 cm, 10 cm, 12 cm
tinggi prisma : 15 cm
 Ditanya : Luas permukaan prisma
?
 Jawab :
 Rumus:
Luas permukaan prisma = (2×luas
alas) + (keliling alas×tinggi)
Luas permukaan prisma =
2×(½×8×10) + {(8+10+12)×15}
Luas permukaan prisma = 80 +
450
Luas permukaan prisma = 530
cm²

12.  Diketahui:
 Prisma tersebut merupakan
prisma segi-3 dengan bentuk alas
segitiga siku-siku t = 7 cm
* Alas Prisma berbentuk segitiga
siku-siku dengan masing-masing
sisi tegak
a = 3 cm, dapat disebut alas
segitiga
b = 4 cm, dapat disebut tinggi
segitiga
 Tentukan volume prisma segitiga
tersebut.

13.  Penyelesaian:
 Volume Prisma
 V = Luas alas × t
Karena alas prisma
berbentuk segitiga,
dapat dihitung
a = 3 cm, sebagai alas (a)
dan b = 4 cm sebagai
tinggi (t)
 La = ½ × a × t
La = ½ × 3 cm × 4 cm
La = 6 cm²
 Sehingga Volume Prisma
V = Luas alas × t
V = 6 cm² × 7 cm
V = 42 cm³

14.  Sebuah prisma telah di
ketahui volume nya yaitu
240 cm3. Dan alas dari
prisma tersebut
berbentuk segitiga siku-
siku dengan panjang
siku” nya yaitu masing”
nya adalah sepanjang
8cm dan 6 cm. Lalu
berapa kah tinggi dari
bangun ruang prisma
tersebut?
 Jawaban :
 Diketahui:
 Volume nya = 240 cm3
 Alas nya = 8 cm dan 6 cm
Ditanya : Berapakah tinggi
dari prisma tersebut?
Volume prisma = luas alas x
tinggi prisma
240cm3 = ( ½ x a x t ) x tinggi
prisma
240cm3 = ( ½ x 8 cm x 6 cm )
x tinggi prisma
240cm3 = 24 cm x tinggi
prisma
 Tinggi prisma = 240cm3 :
24cm = 10cm

15. 1. Suatu limas segiempat alasnya berbentuk segiempat, volumenya 1.350 cm
dengan tinggi limas 18 cm, tentukan volume limas.
1. PENYELESAIAN
2. Dik. V = 1.350 cm3, t = 18 cm,
Dit. S
Jawab:
V = 1/3 x L alas x tinggi
1.350 = 1/3 x Luas alas x 18
1.350 = 6 luas alas
Luas = 1.350/6
Luas = 225 cm2
Karena alas prisma berbentu persegi maka panjang sisi alas prisma
adalah:
L = s2
225 = s2
S = 15 cm

16. 2. Dik. T = 20 cm, a = 3 cm, b = 4 cm
Ditanya: Luas prisma
Jawab.
C=
Luas alas = ½ x 3 x 4 = 6 cm
Keliling alas = 3 + 4 + 5 = 12 cm
Luas prisma = (2x luas alas) + (kel.alas x t)
= (2 x 6) + (12 x 20)
= 12 +240
= 252
Jadi luas prisma adalah 252 cm2
52516943 22

2. Sebuah prisma tingginya 20 cm, dengan alas segitiga siku-siku, panjang
sisi siku-siku adalah 3 cm dan 4 cm. Tentukan luas prirma

17. 3. Sebuah bangun berbentuk limas dengan alas berbentuk persegi dengan
sisi 12 cm. Tentukanlah volume limas tersebut jika tingginya 30 cm!
Penyelesaian:
Diketahui: sisi = 12 cm, tinggi limas = 30 cm
Ditanya: Volume limas
Jawab: Volume limas = 1/3 x luas alas x tinggi
V = 1/3 x (12x12) x 30
V= 1.440 cm3

18. 4. Sebuah limas segiempat persegi dengan panjang sisi 10 cm dengan dengan
tinggi limas 12 cm, maka berapa nilai luas permukaan limas segiempat
tersebut?
Penyelesaian;
Diketahui :
luas alas = 10×10 = 100 cm2
tinggi limas = 12 cm
Ditanya : luas permukaan limas
Jawab. Luas permukaan limas= luas alas + jumlah luas sisi tegak
luas alas = sisi x sisi = 10 x 10 = 100 cm2
jumlah luas sisi tegak = jumlah luas segitiga sisi tegak =4 x luas segitiga QRT
dengan perhitungan pytagoras segitiga TOB, maka tinggi BT adalah 13 cm.
sehingga,
luas segitiga QRT = 1/2 x QR x BT =1/2 x 10 x 13 = 65 cm2
jumlah luas sisi tegak = 4 x luas segitiga QRT = 4 x 65 = 260
Jadi, luas permukaan limas = 100 + 260 = 360 cm2

19. SOAL LATIHAN
 1. Sebuah limas mempunyai 5 titik sudut, dengan
tinggi 4 cm, sisinya berukuran 6 cm.
a. limas apakah yang dimaksud?
b. berapakah luas permukaannya?
2. Sebuah prisma dengan alas persegi memiliki sisi
sepanjang 55 cm, sedangkan tinggi prisma adalah 40
cm, tentukan volume prisma tersebut.