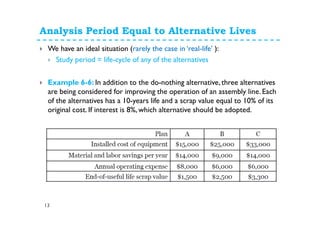
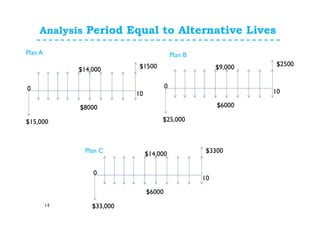
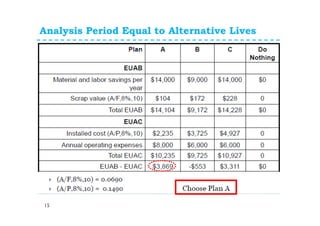
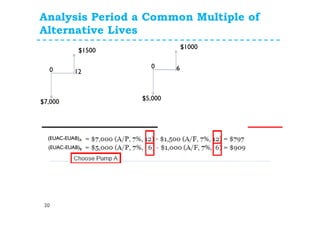
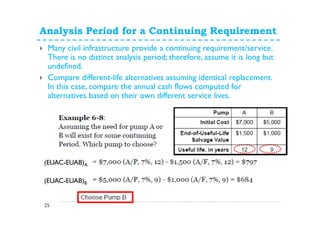
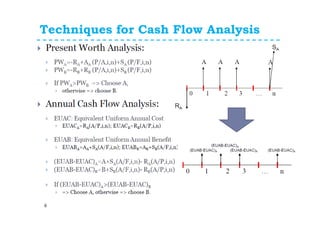
This document provides an overview of annual cash flow analysis techniques for engineering economic evaluations. It defines equivalent uniform annual cost (EUAC) and equivalent uniform annual benefits (EUAB) and explains how to use them to compare alternatives over different time periods, including having the same analysis length, different lengths, infinite lengths, or other periods. The document outlines key concepts like converting cash flows to EUAC/EUAB and discusses analysis periods for alternatives with equal lives, a common multiple of lives, a continuing requirement, or an infinite period. It includes examples of problems applying these techniques. The assignment at the end instructs students to complete 5 problems from the chapter.

1. 7. Annual Cash Flow Analysis
Dr. Mohsin Siddique
Assistant Professor
msiddique@sharjah.ac.ae
Ext: 29431
Date: 18/11/2014
Engineering Economics
University of Sharjah
Dept. of Civil and Env. Engg.

2. 2
Part I

3. Outcome of Today’s Lecture
3
After completing this lecture…
The students should be able to:
Define equivalent uniform annual cost (EUAC) and Equivalent
uniform annual benefits (EUAB)
Resolve an engineering economic analysis problem into its annual
cash flow equivalent
Conduct an equivalent uniform annual worth (EUAW) analysis
for a single investment
Use EUAW, EUAC, and EUAB to compare alternatives with equal,
common multiple, or continuous lives, or over some fixed study
period.

4. Techniques for Cash Flow Analysis
4
Present Worth Analysis
Annual Cash Flow Analysis
Rate of Return Analysis
Incremental Analysis
OtherTechniques:
Future Worth Analysis
Benefit-Cost Ratio Analysis
Payback Period Analysis

5. Annual Cash Flow Analysis
5
Concepts of Annual Cash Flow Analysis
Comparing Alternatives using Annual Cash Flow Analysis:
Same-Length Analysis Period
Different-Length Analysis Periods
Infinite-Length Analysis Period
Other Analysis Periods

6. Techniques for Cash Flow Analysis
6

7. Problem 6-1
7
Compute the value of C for the following diagram, based on “10%
interest rate.
C = $15 + $15 (A/G, 10%, 4)
= $15 + $15 (1.381) = $35.72
0
$15
4 0
G=$15
4
0
= +

8. Problem 6-8
8
As shown in the cash flow diagram, there is an annual disbursement of
money that varies from year to year from $100 to $300 in a fixed pattern
that repeats forever. If interest is 10%, compute the value of A, also
continuing forever, that is equivalent to the fluctuating disbursements.

9. Problem 6-8
9
Pattern
repeats
infinitely
There is a repeating series:; 100 – 200 – 300 – 200. Solving this series for A
gives us the A for the infinite series.

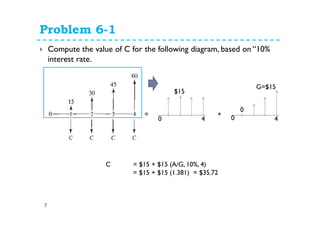
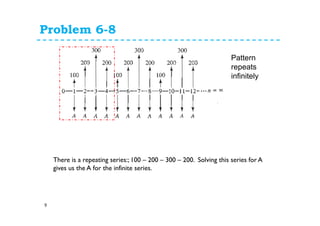
10. Problem 6-8
10
A= $100 + [$100 (P/F, 10%, 2) + $200 (P/F, 10%, 3) + $100 (P/F, 10%, 4)] (A/P, 10%, 4)
= $100 + [$100 (0.8254) + $200 (0.7513) + $100 (0.6830)] (0.3155)
= $100 + [$301.20] (0.3155)
= $195.03
0
$100
4 0
200
4
+
100100

11. Annual Cash Flow Analysis
11
The basic idea is to convert all cash flows to a series of EUAW (equivalent
uniform annual worth):
Net EUAW = EUAB -EUAC
EUAC: Equivalent Uniform Annual Cost
EUAB: Equivalent Uniform Annual Benefit
An expenditure increases EUAC and a receipt of money decreases EUAC.
To convert a PW of a cost to EUAC, use:
EUAC = (PW of cost) (A/P, i%, n)
Where there is salvage value?
A = F(A/F, i%, n)
A salvage value will reduce EUAC and increase EUAB
When there is an arithmetic gradient, use the (A/G, i%, n) factor.
If there are irregular cash flows, try to first find PW of these flows; then,
EUAC may be calculated from this PW.
Criteria for selection of an alternative:
Maximize Net EUAW (EUAB –EUAC)
Minimize EUAC OR Maximize EUAB

12. Analysis Period
12
Five different analysis-period situations occur:
1.Analysis Period Equal to Alternative Lives
2.Analysis Period a Common Multiple
3.Analysis Period for a Continuing Requirement
4. Infinite Analysis Period
5. Some Other Analysis Period:
Analysis period may be equal to life of the shorter-life
alternative, the longer-life alternative, or something
different. In this case, terminal values at the end of a
specific year become very important.

13. Analysis Period Equal to Alternative Lives
13
We have an ideal situation (rarely the case in ‘real-life’ ):
Study period = life-cycle of any of the alternatives
Example 6-6: In addition to the do-nothing alternative, three alternatives
are being considered for improving the operation of an assembly line. Each
of the alternatives has a 10-years life and a scrap value equal to 10% of its
original cost. If interest is 8%, which alternative should be adopted.

14. Analysis Period Equal to Alternative Lives
14
$6000
$25,000
$9,000 $2500
0
10
$8000
$15,000
$14,000 $1500
0
10
$6000
$33,000
$14,000 $3300
0
10
Plan A Plan B
Plan C

15. Analysis Period Equal to Alternative Lives
15

16. Problem 6-32
16

17. Problem 6-32
17
Around the Lake Under the Lake
First Cost $75,000 $125,000
Maintenance $3,000/yr $2,000/yr
Annual Power Loss $7,500/yr $2,500/yr
Property Taxes $1,500/yr $2,500/yr
Salvage Value $45,000 $25,000
Useful Life 15 years 15 years

18. Problem 6-32
18
0 15
$75,000
$3000
$7500
$1500
$45000
0 15
$125,000
$2000
$2500
$2500
$25000
Around the Lake Under the Lake
Around the Lake
EUAC = $75,000 (A/P, 7%, 15) + $12,000 - $45,000 (A/F, 7%, 15)
= $75,000 (0.1098) + $12,000 - $45,000 (0.0398)
= $18,444
Under the Lake
EUAC = $125,000 (A/P, 7%, 15) + $7,000 - $25,000 (A/F, 7%, 15)
= $125,000 (0.1098) + $7,000 - $25,000 (0.0398)
= $19,730
Go around the lake.

19. Analysis Period a Common Multiple of
Alternative Lives
19
Assume a replacement with an identical item with same cost and
performance.When the lives of two alternatives vary, one can use a
common multiple of the two lives to determine the better project.
Nevertheless, compare alternatives based on their own service lives.
Example 6-7: Two pumps are being considered for purchase. If interest is
7%, which pump should be bought. Assume that Pump B will be replaced
after its useful life by the same one.

20. Analysis Period a Common Multiple of
Alternative Lives
20
(EUAC-EUAB)A
(EUAC-EUAB)B
0
$7,000
$1500
12
0
$5,000
$1000
6

21. Analysis Period with a Repeatability
Assumption
21
If two or more alternatives have
unequal lives, only evaluate the
annual worth (AW) for one life
cycle of each alternative
The annual worth of one cycle
is the same as the annual worth
of all future cycles
Under the circumstances of identical replacement (repeatability):

22. Problem 6-37
22

23. Problem 6-37
23
Machine X
EUAC= $5,000 (A/P, 8%, 5)= $5,000 (0.2505) = $1,252
MachineY
EUAC= $8,000(A/P, 8%, 12) + $150 - $2,000 (A/F, 8%, 12)
=8000(0.1327) +150 -2000( 0.0527) = $1,106
Select MachineY.
$5,000
0 5
$150
$8,000
$2000
0
12
Machine X MachineY

24. 24
Part II

25. Analysis Period for a Continuing Requirement
25
Many civil infrastructure provide a continuing requirement/service.
There is no distinct analysis period; therefore, assume it is long but
undefined.
Compare different-life alternatives assuming identical replacement.
In this case, compare the annual cash flows computed for
alternatives based on their own different service lives.
(EUAC-EUAB)A
(EUAC-EUAB)B

26. Infinite Analysis Period
26
At times we may have an alternative with a finite useful life in an infinite
analysis period situation.
With identical replacement:
EUAC for infinite analysis period = EUAC for limited life

27. Infinite Analysis Period
27
EUAC for infinite analysis period = P (A/P ,i, ∞)+ any other annual (costs-benefits)
(A/P, i,∞) = i
(EUAC-EUAB)A= $100(A/P,8%, ∞) -$10.00 = $100* 0.08 -$10.00 = $-2.00
(EUAC-EUAB)B= $150(A/P,8%,20) -$17.62 = $150 * 0.1019-$17.62 =$-2.34
(EUAC-EUAB)C= $200(A/P,8%,5) -$55.48 = $200 * 2.505 -$55.48 =$-5.38
Select alternative C

28. Problem 6-41
28

29. Problem 6-41
29
Because we may assume identical replacement, we may compare 20 years
of B with an infinite life for A by EUAB – EUAC.
Alternative A
EUAB – EUAC (for an inf. period) = $16 - $100 (A/P, 10%, ∞)
= $16 - $100 (0.10)= +$6.00
Alternative B
EUAB – EUAC (for 20 yr. period) = $24 - $150 (A/P, 10%, 20)
= $24 - $150 (0.1175)= +$6.38
Choose Alternative B.

30. Summary
30
Popular analysis technique:
Easily understood -results are reported in $ per time period,
usually $ per year
AW method is often preferred to the PW method
Only have to evaluate one life cycle of an alternative
Assumption for AW method: Cash flows in one cycle are assumed
to replicate themselves in future cycles
No need to convert lifetimes of all projects to their least common
multiple!
AW offers an advantage for comparing different-life alternatives
For infinite life alternatives, simply multiply P by i to get AW value

31. Assignment # 7
31
6.7, 6.16, 6.21, 6.29, 6.42
Date of Submission: _____________
Assignment should be hand written

32. 32
ThankYou
Feel Free to Contact
msiddique@sharjah.ac.ae
Tel. +971 6 5050943 (Ext. 2943)