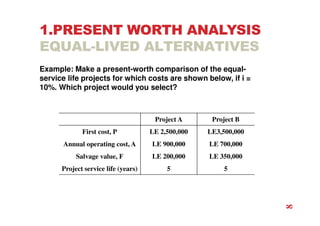
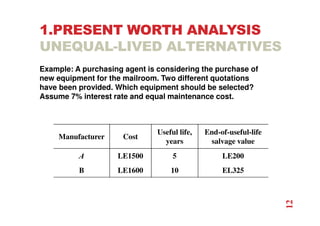
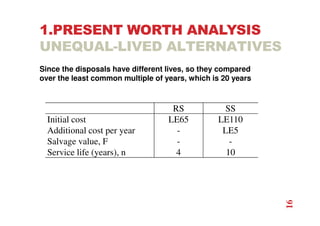
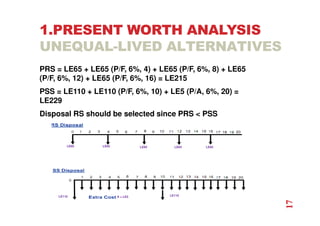
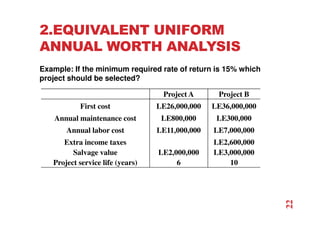
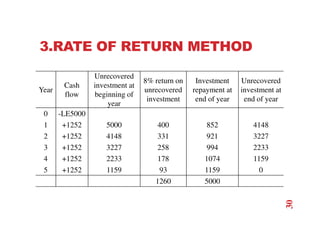
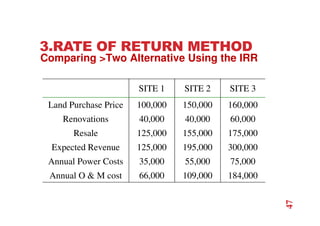
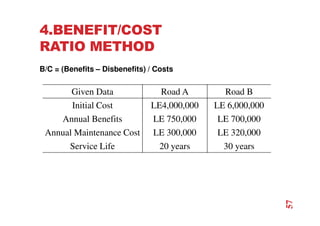
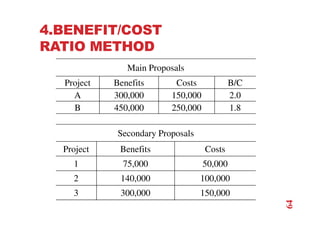
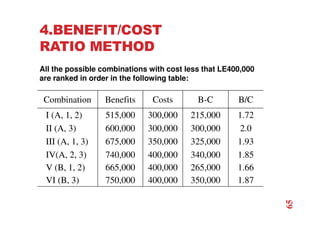
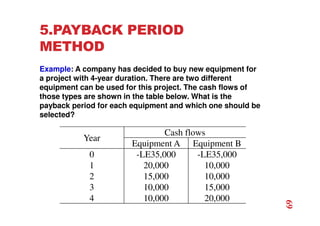
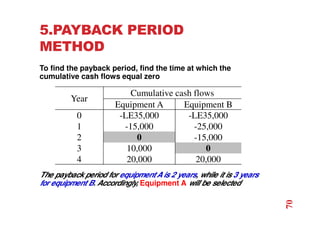
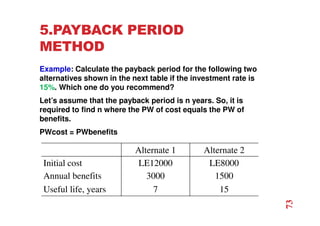
The document discusses economic evaluation methods for investment alternatives, highlighting techniques such as present worth analysis, life cycle costing, and rate of return method. It emphasizes the importance of establishing criteria for investment decisions, assessing cash flows, and comparing projects with different service lives. Additionally, it illustrates these methods through various examples to demonstrate practical applications in decision-making.



































































![INFLATION
i’ = i + f + if = 0.12 + 0.11 + 0.12 × 0.11 = 0.243 = 24.3%
Pa = LE60,000
Pb = A[ ((1 + i’)n – 1)) / (i’(1 + i’)n )]
= 16000 [(1.24312 -1) / 0.243(1.24312)] = LE61,003
Pc = 50000 / (1.243)3 + 80000 / (1.243)5 = LE52,996
Then, option b is preferred
81](https://image.slidesharecdn.com/6-241223083443-bd2bc9ac/85/6-alternative_analysis_cb311_spring-2015-1-pdf-81-320.jpg)

