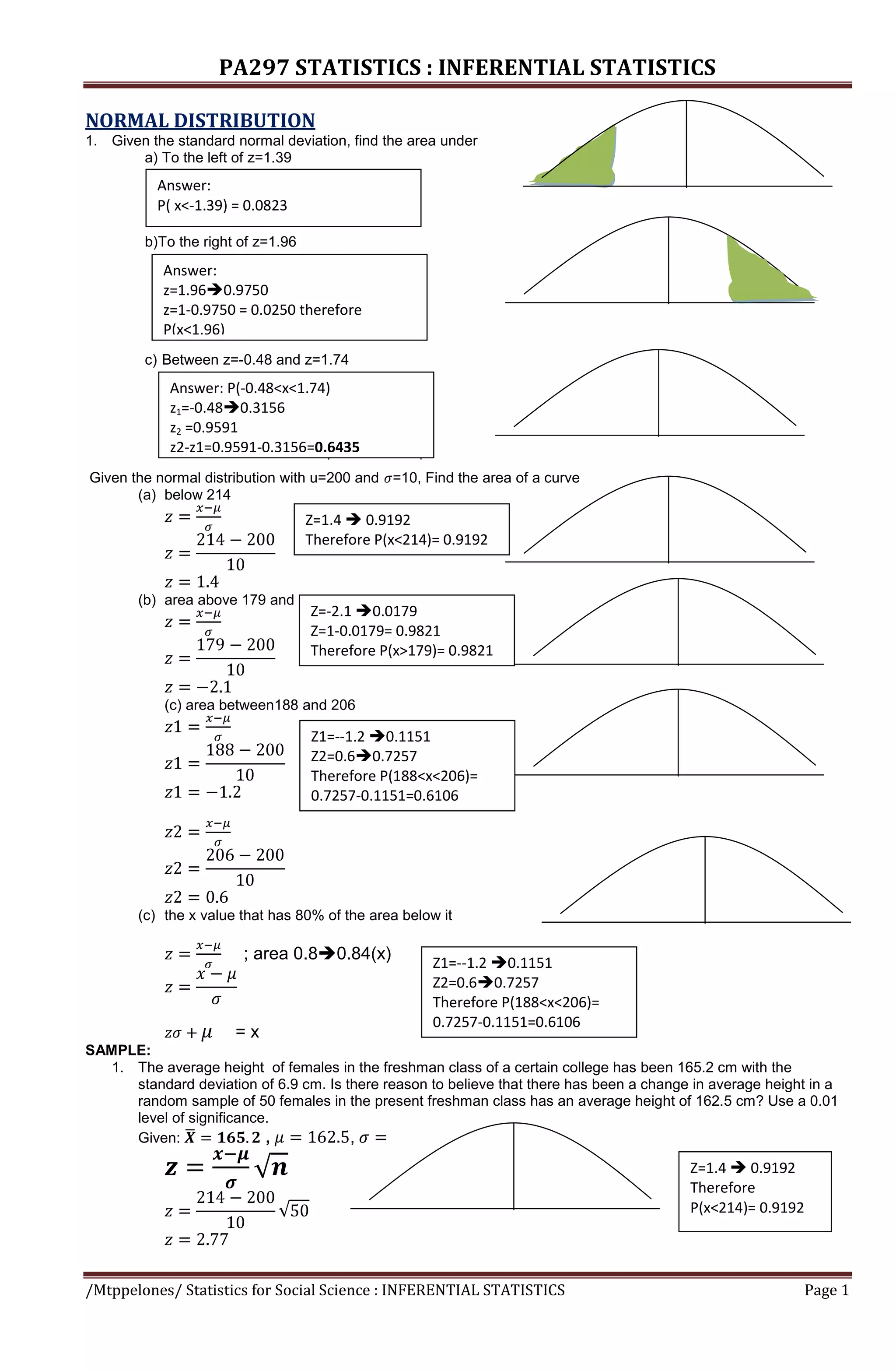
The document discusses key concepts in statistical inference including estimation, confidence intervals, hypothesis testing, and types of errors. It provides examples and formulas for estimating population means from sample data, calculating confidence intervals, stating the null and alternative hypotheses, and making decisions to accept or reject the null hypothesis based on a significance level.

1. NORMAL DISTRIBUTION<br />Given the standard normal deviation, find the area under

2. To the left of z=1.39

3. Answer:P( x<-1.39) = 0.0823

4. To the right of z=1.96Answer:z=1.960.9750z=1-0.9750 = 0.0250 thereforeP(x<1.96)<br /> Between z=-0.48 and z=1.74Answer: P(-0.48<x<1.74)z1=-0.480.3156z2 =0.9591z2-z1=0.9591-0.3156=0.6435<br /> Given the normal distribution with u=200 and σ=10, Find the area of a curve<br />below 214

5. Z=1.4 0.9192Therefore P(x<214)= 0.9192z=x-μσ

6. z=214-20010

7. z=1.4

8. Z=-2.1 0.0179Z=1-0.0179= 0.9821Therefore P(x>179)= 0.9821area above 179 and z=x-μσ<br />z=179-20010<br />z=-2.1<br />(c) area between188 and 206Z1=--1.2 0.1151Z2=0.60.7257Therefore P(188<x<206)= 0.7257-0.1151=0.6106z1=x-μσ<br />z1=188-20010<br />z1=-1.2<br />z2=x-μσ<br />z2=206-20010<br />z2=0.6<br />the x value that has 80% of the area below it Z1=--1.2 0.1151Z2=0.60.7257Therefore P(188<x<206)= 0.7257-0.1151=0.6106z=x-μσ; area 0.80.84(x)<br />z=x-μσ