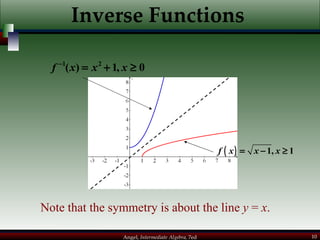
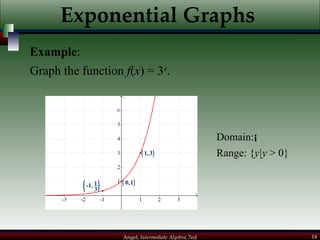
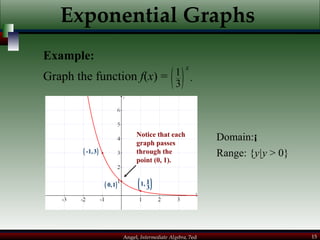
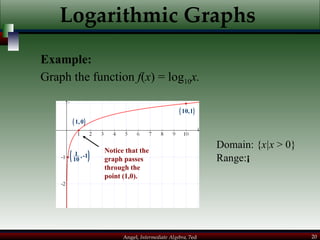
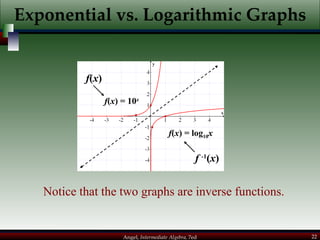
This document provides an overview of exponential and logarithmic functions. It covers composite and inverse functions, exponential functions, logarithmic functions, properties of logarithms, common logarithms, exponential and logarithmic equations, and natural exponential and logarithmic functions. Example problems are provided to illustrate each concept.

1. Exponential and Logarithmic Functions Chapter 9

2. Chapter Sections 9.1 – C omposite and Inverse Functions 9.2 – Exponential Functions 9.3 – Logarithmic Functions 9.4 – Properties of Logarithms 9.5 – Common Logarithms 9.6 – Exponential and Logarithmic Equations 9.7 – Natural Exponential and Natural Logarithmic Functions

3. § 9.1 Composite and Inverse Functions

4. Composite Functions The composite function is defined as x + 2 is substituted into each x in f ( x ). g ( x ) is substituted into each x in f ( x ). Example: Given f ( x ) = x 2 – 3, and g ( x ) = x + 2, find .

5. Composite Functions Example: Given f ( x ) = x 2 – 3, and g ( x ) = x + 2, find x 2 - 3 is substituted into each x in g ( x ). f ( x ) is substituted into each x in g ( x ).

6. One-to-One Functions For a function to be one-to-one, it must not only pass the vertical line test, but also the horizontal line test. A function is a one-to-one function if each value in the range corresponds with exactly one value in the domain. x y Function x y Not a one-to-one function x y One-to one function

7. Inverse Functions Function: {(2, 6), (5,4), (0, 12), (4, 1)} If f ( x ) is a one-to-one function with ordered pairs of the form ( x , y ), its inverse function , f -1 ( x ), is a one-to-one function with ordered pairs of the form ( y , x ). Inverse Function: {(6, 2), (4,5), (12, 0), (1, 4)} Only one-to-one functions have inverse functions. Note that the domain of the function becomes the range of the inverse function, and the range becomes the domain of the inverse function.

8. Inverse Functions Replace f ( x ) with y . Interchange the two variables x and y . Solve the equation for y . Replace y with f –1 ( x ). (This gives the inverse function using inverse function notation.) To Find the Inverse Function of a One-to-One Function Example: Find the inverse function of Graph f ( x ) and f ( x ) –1 on the same axes.

9. Inverse Functions Replace f ( x ) with y . Interchange x and y . Solve for y . Replace y with f –1 ( x ) . Example continued:

10. Inverse Functions Note that the symmetry is about the line y = x .

11. Composites and Inverses If two functions f ( x ) and f –1 ( x ) are inverses of each other, . Example: Show that . and

12. § 9.2 Exponential Functions

13. Exponential Functions For any real number a > 0 and a  1, f ( x ) = a x is an exponential function. For all exponential functions of this form, The domain of the function is The range of the function is The graph passes through the points

14. Exponential Graphs Example : Graph the function f ( x ) = 3 x . Range: { y|y > 0} Domain:

15. Exponential Graphs Range: { y|y > 0} Notice that each graph passes through the point (0, 1). Example: Domain: Graph the function f ( x ) =

16. § 9.3 Logarithmic Functions

17. Exponential Functions For all positive numbers a , where a  1, y = log a x means x = a y . y = log a x logarithm (exponent) base number means x = a y number base exponent

18. Exponential Functions Exponential Form Logarithmic Form 5 0 = 1 log 10 1= 0 2 3 = 8 log 2 8= 3

19. Logarithmic Functions For all logarithmic functions of the form y = log a x or f ( x ) = log a x , where a > 0, a  1, and x > 0, The domain of the function is . The range of the function is . The graph passes through the points

20. Logarithmic Graphs Domain: { x|x > 0} Graph the function f ( x ) = log 10 x. Notice that the graph passes through the point (1,0). Example: Range:

21. Exponential vs. Logarithmic Graphs Exponential Function Logarithmic Function y = a x ( a > 0, a  1) y = log a x ( a > 0, a  1) Domain: Range: Points on Graph: x becomes y y becomes x

22. Exponential vs. Logarithmic Graphs Notice that the two graphs are inverse functions. f ( x ) f - 1 ( x ) f ( x ) = log 10 x f ( x ) = 10 x

23. § 9.4 Properties of Logarithms

24. Product Rule For positive real numbers x , y , and a , a  1, Product Rule for Logarithms Example: log 5 (4 · 7) = log 5 4 + log 5 7 log 10 (100 · 1000) = log 10 100 + log 10 1000 = 2 + 3 = 5

25. Quotient Rule For positive real numbers x , y , and a , a  1, Quotient Rule for Logarithms Example: Property 1

26. Power Rule If x and y are positive real numbers, a  1, and n is any real number, then Power Rule for Logarithms Example : Property 2

27. Additional Properties If a > 0, and a  1, Additional Properties of Logarithms Example : Property 5 Property 4

28. Combination of Properties Example : Write the following as the logarithm of a single expression. Power Rule Product Rule Quotient Rule

29. § 9.5 Common Logarithms

30. Common Logarithms The common logarithm of a positive real number is the exponent to which the base 10 is raised to obtain the number. If log N = L , then 10 L = N. The antilogarithm is the same thing as the inverse logarithm. If log N = L , then N = antilog L . log 962 = 2.98318 Number Exponent antilog 2.98318 = 962 Number Exponent Example :

31. § 9.6 Exponential and Logarithmic Equations

32. Properties If x = y , a x = a y . If a x = a y , then x = y . If x = y , then log b x = log b y ( x > 0, y > 0). If log b x = log b y , then x = y ( x > 0, y > 0). Properties for Solving Exponential and Logarithmic Equations Properties 6a-6d

33. Solving Equations Example : Rewrite each side with the same base. Property 6b. Solve for x .

34. Solving Equations Example : Product Rule Property 6d. Check: Stop! Logs of negative numbers are not real numbers. True

35. § 9.7 Natural Exponential and Natural Logarithmic Functions

36. Definitions The natural exponent function is f ( x ) = e x where e  2.71823. Natural logarithms are logarithms to the base e. Natural logarithms are indicated by the letters ln. log e x = ln x Example : ln 1 = 0 ( e 0 = 1) ln e = 1 ( e 1 = e )

37. Change of Base Formula For any logarithm bases a and b , and positive number x, Change of Base Formula This is very useful because common logs or natural log can be found using a calculator. Example : Note that the natural log could have also been used.

38. Properties Notice that these are the same properties as those for the common logarithms. Properties for Natural Logarithms Product Rule Power Rule Quotient Rule Additional Properties for Natural Logarithms and Natural Exponential Expressions Property 7 Property 8

39. Solving Equations Example : Solve the following equation. Product Rule Simplify Property 6d Solve for x . Check solutions in original equation. (You will notice that only the positive 7 yields a true statement.)

40. Applications In 2000, a lake had 300 trout. The growth in the number of trout is estimated by the function g ( t ) = 300 e 0.07 t where t is the number of years after 2000. How many trout will be in the lake in a) 2003? b) 2010? In the year 2000, t = 0 . (Notice that f (0) =300 e 0.07(0) = 300 e 0 = 300, the original number of trout.) In the year 2003, t = 3. g (3) = 300 e 0.07(3) = 300 e 0.21 = 300(1.2337)  370 trout in 2003 . In the year 2010, t = 10. g (10) = 300 e 0.07(10) = 300 e 0.70 = 300(2.0138)  604 trout in 2010 . Example: