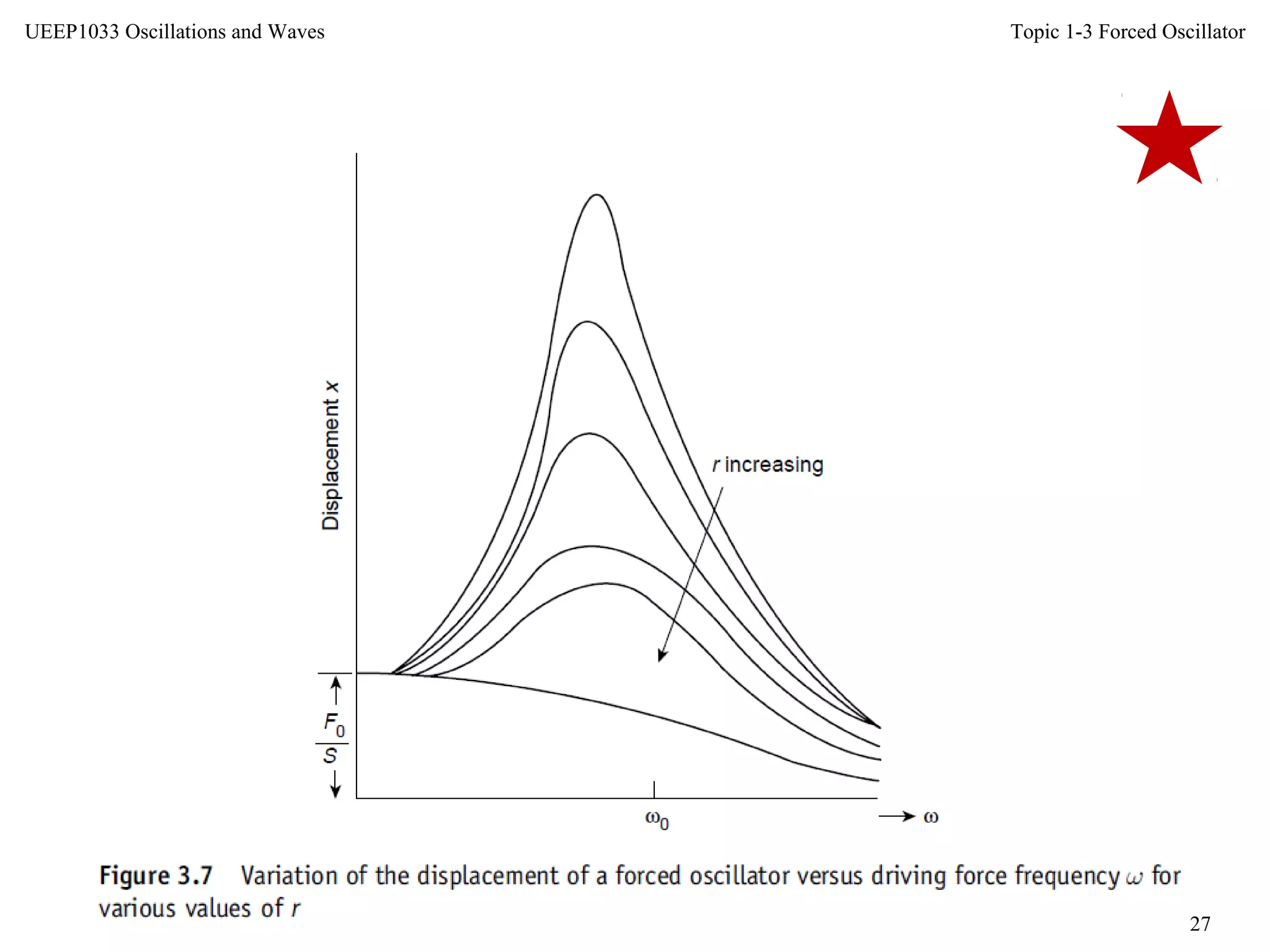
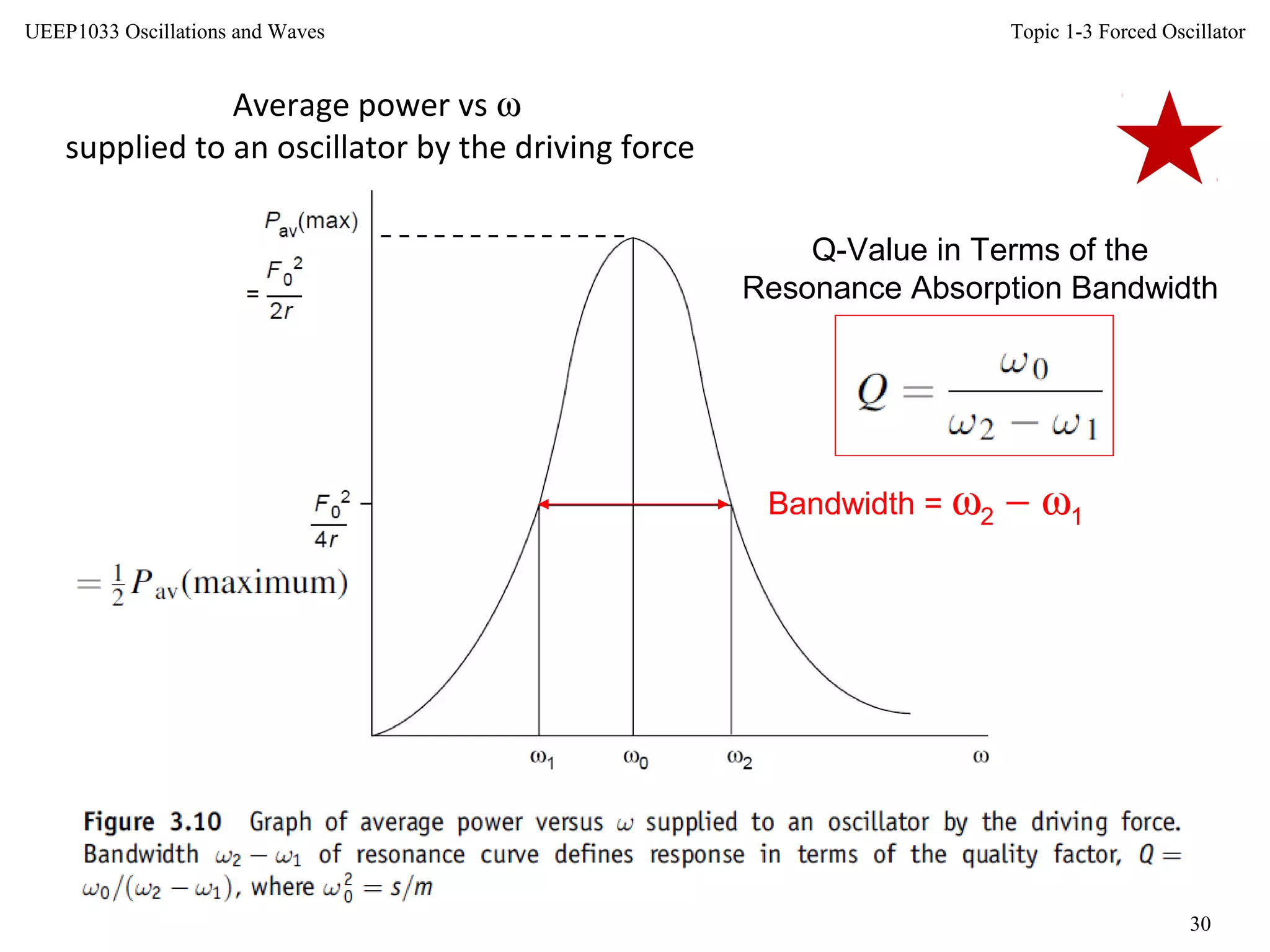
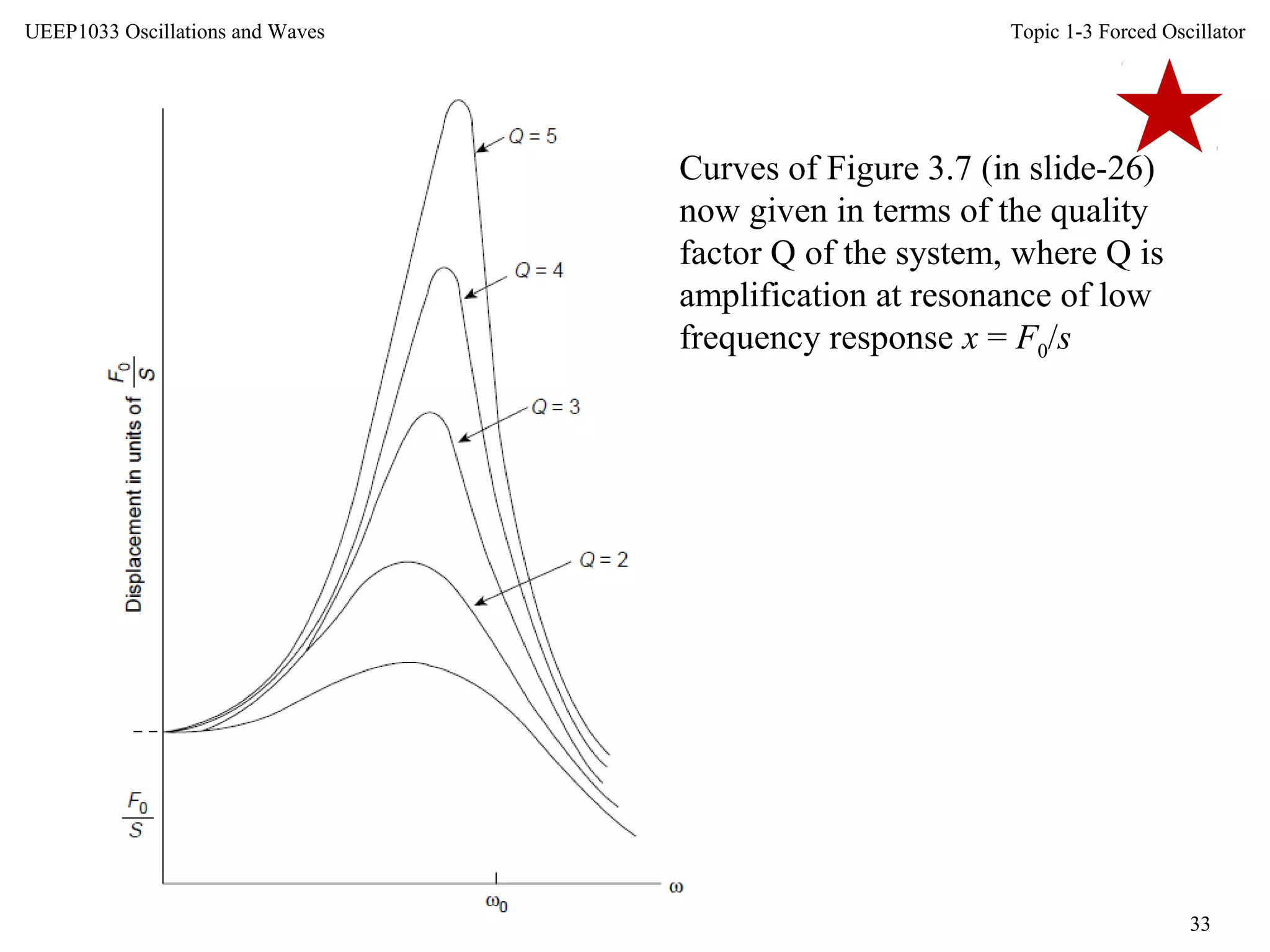
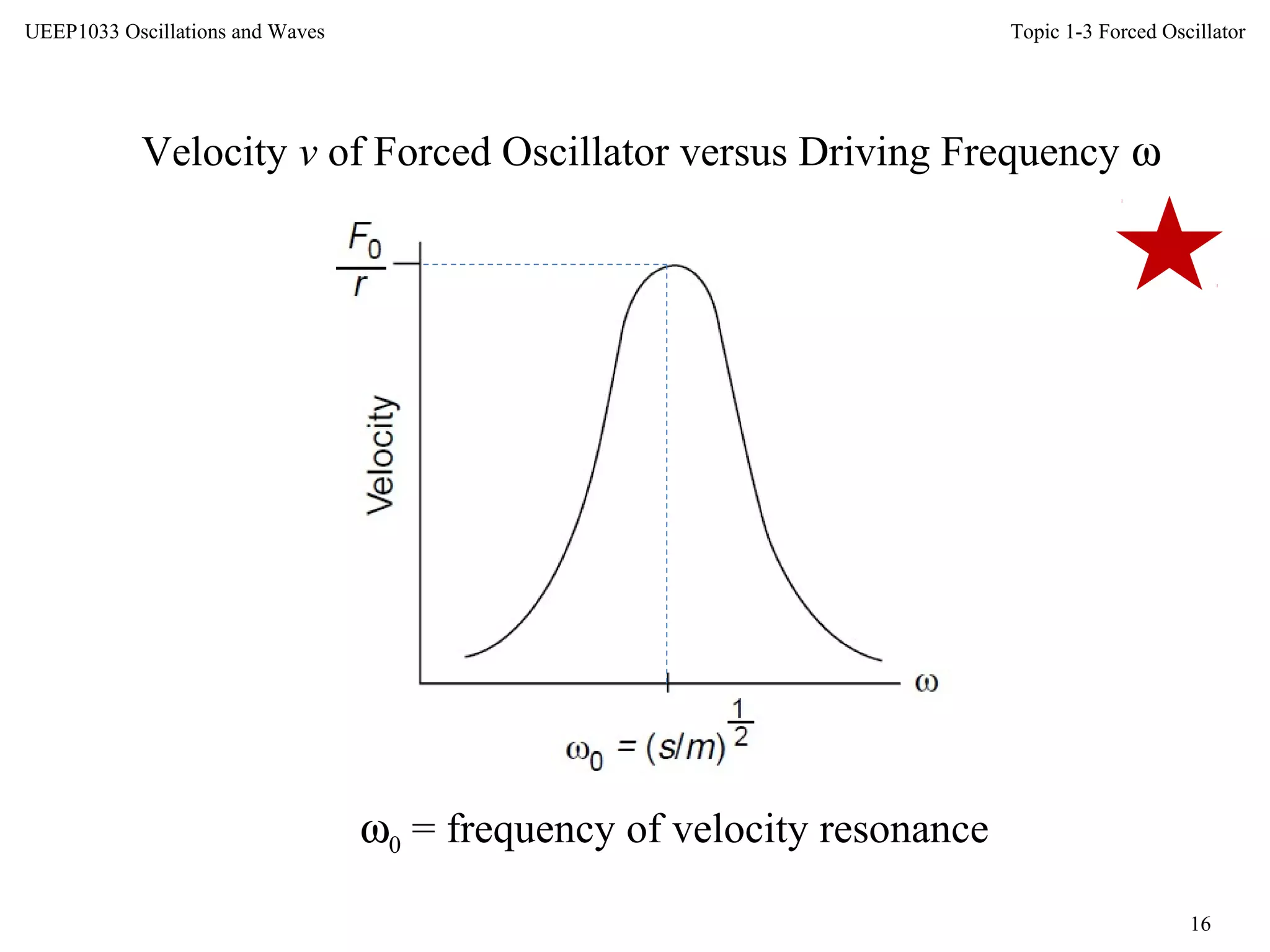
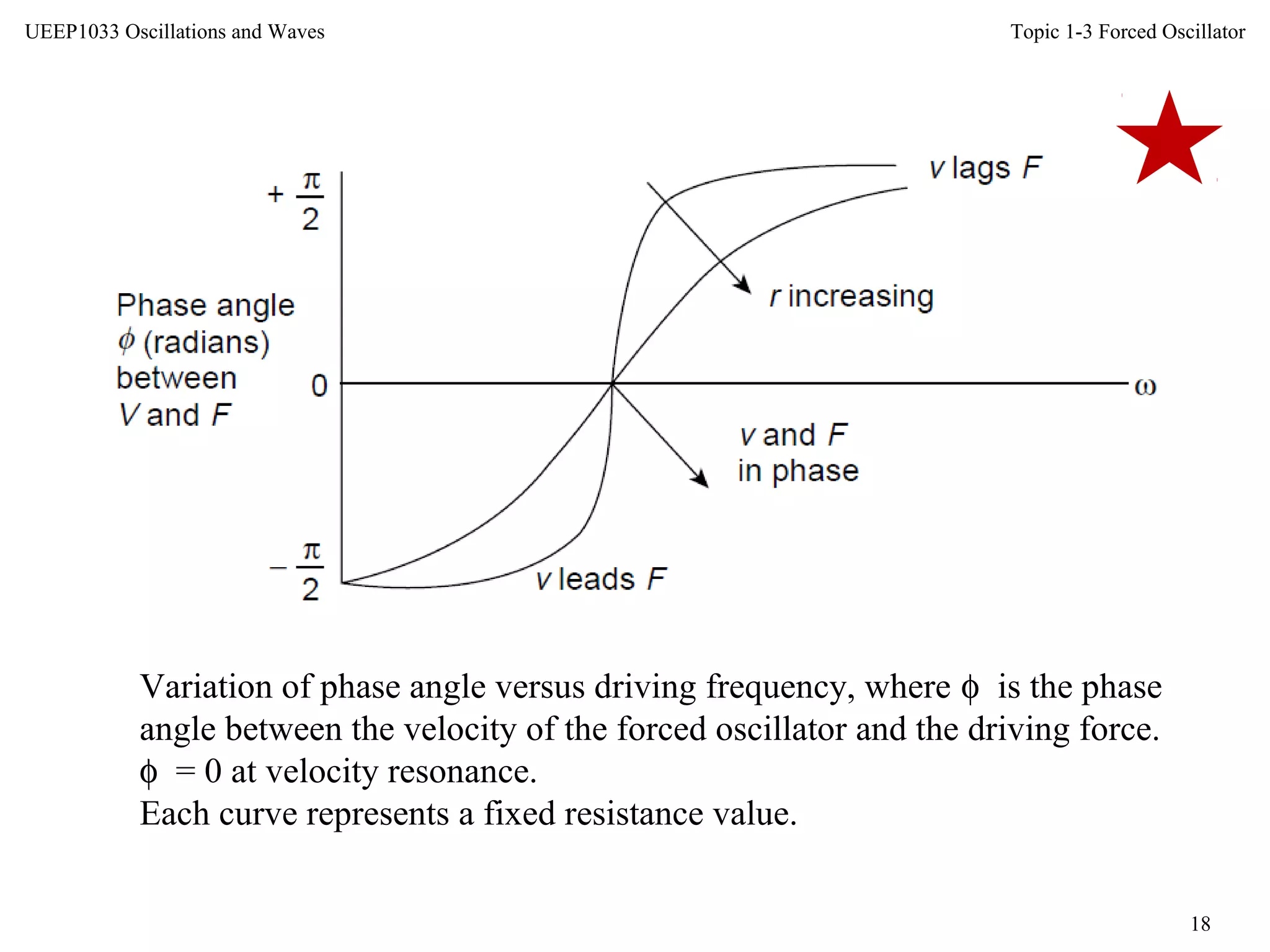
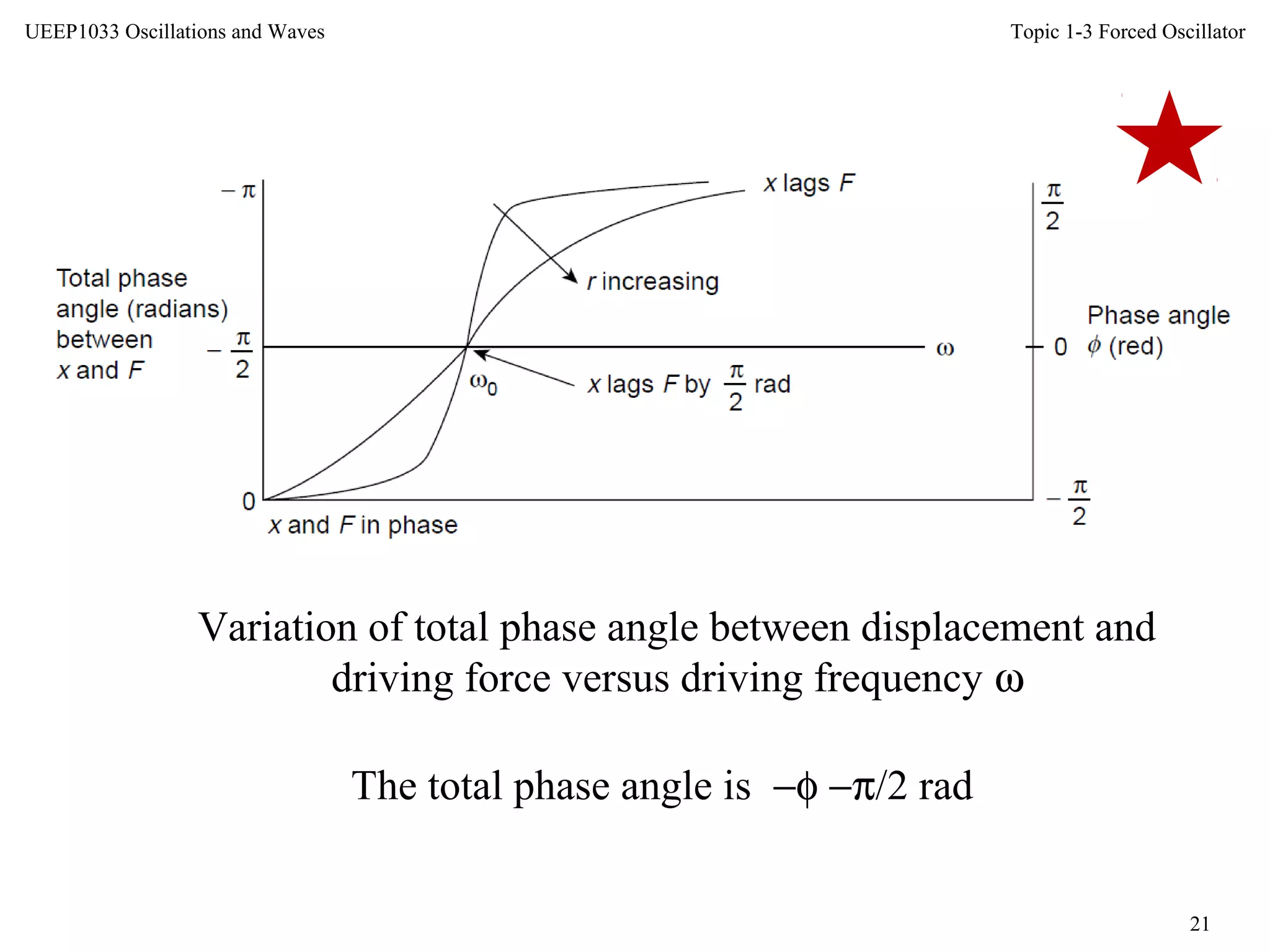
This document discusses forced oscillators and their behavior. It describes how a forced oscillator has both a transient term that decays over time and a steady-state term that describes the oscillator's long-term behavior. The steady-state behavior is defined by the phase difference between the oscillator's displacement and the driving force, as well as the maximum displacement amplitude. The document also examines how the oscillator's velocity, displacement, impedance, power input, and Q-factor vary with the driving force frequency.
















![Topic 1-3 Forced Oscillator
22
UEEP1033 Oscillations and Waves
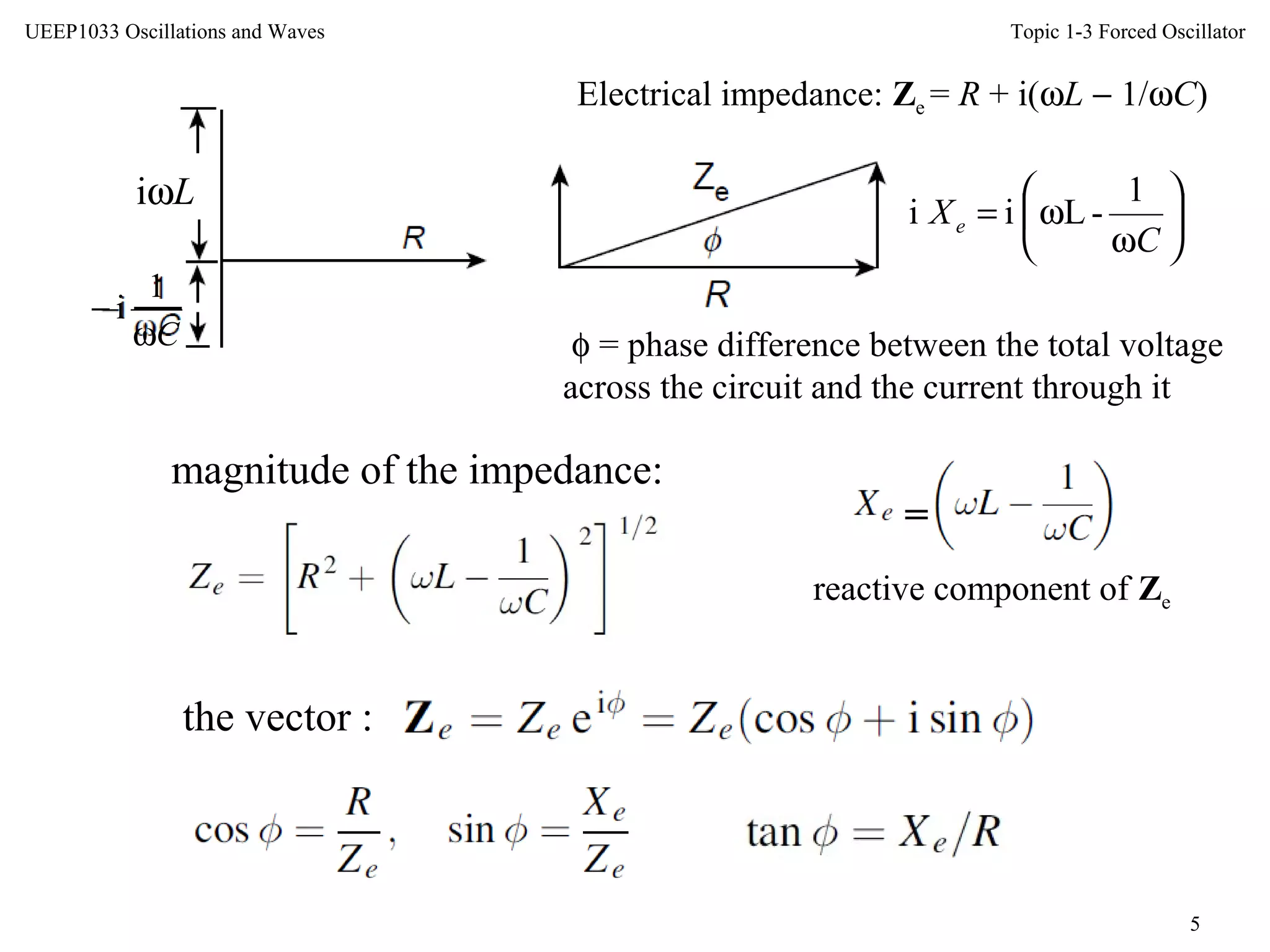
amplitude of the displacement : x = Fo /ωZm
At low frequencies: Zm = [r2
+ (ωm − s/ω)2
]1/2
→ s/ω
⇒ x ≈ Fo /(ωs/ ω) = Fo /s
At high frequencies: Zm → ωm
⇒ x ≈ Fo /(ω2
m)
At very large frequencies: x → 0](https://image.slidesharecdn.com/topic3forcedoscillator-140705124726-phpapp01/75/Topic-3-forced-oscillator-22-2048.jpg)