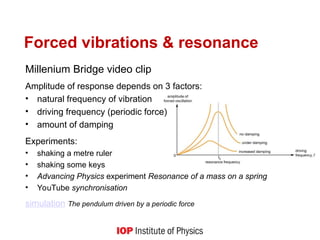
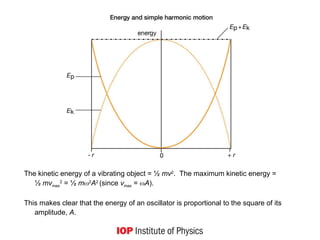
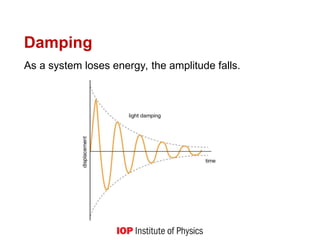
The document discusses the fundamental concepts of simple harmonic motion (SHM) and its historical background, emphasizing the need for students to understand radians, trigonometry, and the small angle approximation. It outlines various experiments and questions to help students explore SHM, including the role of restoring forces, amplitude, damping, and the relationship between displacement, velocity, and acceleration. Additionally, it touches on resonance and energy dynamics in vibrating systems, supported by historical examples and practical applications.

1. TJMRMHTGRE

2. HTFEW

3. GFD

6. Teaching challenges
Students must first be familiar with radians, trigonometry
and the small angle approximation .
A double maths challenge:
1. linking the kinematic description of SHM with an
understanding of how the force changes.
2. differentiating trigonometric functions.

 
sin

7. A brief history & contexts
The study of SHM started with Galileo’s pendulum experiments
(1638, Two new sciences).
Huygens, Newton & others developed further analyses.
• pendulum – clocks, seismometers
• ALL vibrations and waves - sea waves, earthquakes, tides,
orbits of planets and moons, water level in a toilet on a windy
day, acoustics, AC circuits, electromagnetic waves, vibrations
molecular and structural e.g. aircraft fuselage, musical
instruments, bridges.

8. Getting a feel for SHM 1
Careful observation of a big pendulum.
There is an equilibrium (rest) position. Displacement, s, is the
distance from equilibrium.
Discuss, in pairs
1. Where is the mass moving fastest, slowest?
2. Where is the mass’s acceleration maximum, zero?
3. Does the time for one complete oscillation depend on the amplitude?
4. What causes the mass to overshoot its equilibrium position?
5. What forces act on the mass? When is the unbalanced force at a
maximum value, zero? Do these predictions fit your observations
about the acceleration?

9. Getting a feel for SHM 2
A circus of experiments (in small groups)
• torsional pendulum
• vibrating lath
• oscillating water column
• bouncing ping-pong ball
• ball rolling in a shallow bowl
• wig-wag
• ball-bearing on rails of different shapes
Answer the same set of questions about changing
velocities, accelerations and forces.

10. Describing oscillations
The system goes through a recurring cycle.
Amplitude, A, is the maximum displacement.
If the cycle repeat time is independent of amplitude (the oscillations is
isochronous), then you can define a periodic time, T, and frequency, f.
A restoring force tries to return system to equilibrium.
The system has inertia and overshoots equilibrium position.

11. Damping
As a system loses energy, the amplitude falls.

12. Trolley between springs
k is the constant relating restoring force to
displacement, m is mass
The - sign indicates a and s have opposite directions.
The acceleration is
• always directed towards the equilibrium position
• proportional to displacement
s
m
k
a
ks
ma
F












13. How does displacement vary?
[empirically]
PP experiment:
Broomstick pendulum, sinusoidal motion
Obtain a graph of displacement against time

14. How does velocity vary?
How does acceleration vary?
[empirical result by datalogging]
PP experiment:
Investigating a mass-on-spring oscillator

16. The SHM auxiliary circle
An imaginary circular motion gives a mathematical
insight into SHM. Its angular velocity is .
Physlets animation ‘The connection between SHM and circular motion’
The time period of the motion,
The frequency of the motion,
Displacement of the SHM,
.
2



T
.
2
1




T
f
).
(
cos t
A
s 


17. SHM equations
Displacement
At t = 0, the object is released from its max displacement.
The velocity, v, (rate of change of displacement) is then given by:
The acceleration, a, (rate of change of velocity) is:
Note that
)
(
cos t
A
s 

)
(
sin
d
d
t
A
t
s
v 




  s
f
s
a
2
2
2
 




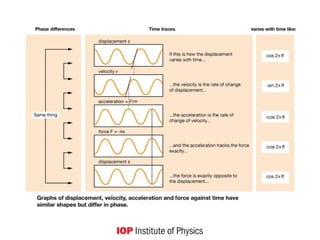
18. Other symbols, relationships
Displacement,
At t =0, the object passes through its equilibrium position.
Phase relationship, 
Try the Geogebra simulation.
)
2
sin(
)
sin( ft
A
t
A
s 
 

)
sin(
)]
cos(
[
)
cos(
)]
sin(
[
2
t
A
t
A
dt
d
a
t
A
t
A
dt
d
v













)
sin( 
 
 t
A
s

19. Maximum values of quantities
Simple harmonic motion:
maximum displacement = A
maximum velocity = A=fA
maximum acceleration = A2
= (f)2
A
Circular motion:
displacement = r
velocity = r
acceleration = r2

20. Problems session 1
Advancing Physics (AP) ‘Quick check’, Q 1 – 4 only.

21. Two particular systems
Mass-on-spring,
Simple pendulum,
(for small angle oscillations)
k
m
T 
2

g
l
T 
2


22. Forced vibrations & resonance
Millenium Bridge video clip
Amplitude of response depends on 3 factors:
• natural frequency of vibration
• driving frequency (periodic force)
• amount of damping
Experiments:
• shaking a metre ruler
• shaking some keys
• Advancing Physics experiment Resonance of a mass on a spring
• YouTube synchronisation
simulation The pendulum driven by a periodic force

23. The kinetic energy of a vibrating object = ½ mv2
. The maximum kinetic energy =
½ mvmax
2
= ½ m2
A2
(since vmax = A).
This makes clear that the energy of an oscillator is proportional to the square of its
amplitude, A.

24. Problems session 2
In order of difficulty:
AP Quick Check Q 5,6
Practice in Physics questions on SHM
AP Oscillator energy and resonance
Energy and pendulums TAP 305-5

25. Endpoints
Video clip: The Tacoma Narrows bridge disaster
Puget Sound, Washington state, USA, November 1940