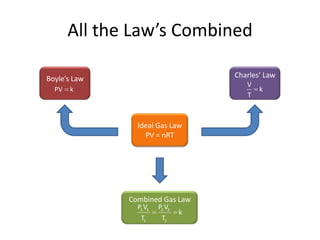
The document discusses several gas laws: - Boyle's law states that at constant temperature, the volume of a gas is inversely proportional to its pressure. - Charles' law states that at constant pressure, the volume of a gas is directly proportional to its kelvin temperature. - Combined gas law allows calculation of gas properties when temperature and/or pressure change. It also discusses concepts like the kinetic molecular theory of gases and how real gases deviate from ideal gas behavior due to intermolecular forces and molecular size. Sample calculations demonstrate use of the gas laws and kinetic theory.

1. Gas Laws
Section 3.2

2. Boyle’s Law
At a constant temperature, the volume of a given mass of any gas
is inversely proportional to the pressure of the gas.
http://www.chem.iastate.edu/group/Greenbowe/sections/projectfolder/flashfiles/gaslaw/boyles_law_graph_new.swf

3. Charles’ Law
At a constant pressure, the volume of a given mass of any gas
is directly proportional to the Kelvin Temperature.
http://www.chem.iastate.edu/group/Greenbowe/sections/projectfolder/flashfiles/gaslaw/charles_law.swf

4. Gay – Lussac’s Law of Combining Volumes
When a gases react, the
volumes consumed in the
reaction bear a simple
whole number ratio to
each other, and to the
volumes of any gaseous
product of the reaction, if
all volumes are measured
under the same
conditions of temperature
and pressure.

5. Avogadro’s Law
Equal volumes of (ideal) gases, contain the
same number of particles, or molecules, under
the same conditions.

6. All the Law’s Combined
Charles’ Law
Boyle’s Law
PV
V
T
k
Ideal Gas Law
PV = nRT
Combined Gas Law
P1 V1
T1
P2 V2
T2
k
k

7. The Combined Gas Laws
Combined Gas Law
P1 V1
T1
P2 V2
T2
•
•
P1, V1, and T1 are the initial pressure, volume and Kelvin temperature.
P2, V2 and T2 are the final pressure, volume and Kelvin temperature.
•
•
•
Pressure can be in any units as long as it’s the same for P1 and P2.
Volume can be in any units as long as it’s the same for V1 and V2.
Temperature must be in Kelvin’s for T1 and T2.
To convert from degrees to Kelvin’s add on 273.
For example 25o = 25 + 273 = 298 K

8. A sample of gas exerts a pressure of 83,326 Pa in a 300 cm3 vessel at 25oC.
What pressure would this gas sample exert if it were placed in a 500 cm3
container at 50oC?
P1
83,326 Pa
P2
?
V1
300cm3
V2
500cm3
T2
50 273 323K
T1 25 273 298 K
P1 V1 P2 V2
T1
T2
83,326 300 P2 500
298
323
83,326 300 323
P2
500
54,189.86 Pa P2
Temperature must
be in Kelvin’s

9. A sample of gas occupies 250 cm3 at 27oC. What volume will it occupy at
35oC if there is no change in pressure?
Note : As the pressure is constant, it can be left out of the equation.
V1
300mL
T1 27 273 300K
V1 V2
T1 T2
250 V2
300 308
250 308
V2
300
256.67 cm3 P2
V2 ?
T2
35 273 308K

10. S.T.P.
(Standard, Temperature and Pressure)
• Scientists who first studied gases soon realised
that the pressure and temperature controlled
the volume observed for a gas sample.
• Therefore to compare different gas samples,
they defined a set of reference conditions.
• These conditions are known as standard,
temperature and pressure, or simply STP, and
are 273 K, and 101,325 Pa.

11. What would the volume of a gas at STP if it was found to occupy a volume
of 255 cm3 at 25oC and 101,000 Pa?
P1 101,325 Pa
P2 101,000 Pa
V1 ?
T1 273K
V2 255cm3
T2 25 273 298K
P1 V1 P1 V2
T1
T2
101,325 V1 101,000 255
273
298
101,000 255 273
V1
298 101,325
V1 232.86cm3
S tandard temperature 273 K
S tandardpressure 101,325 Pa

12. The Kinetic Theory of Gases
The kinetic theory of gases was developed by James Clerk Maxwell
and Ludwig Boltzmann.
This theory assumes that:
1.
2.
3.
4.
5.
Gases are made up of particles whose diameters are negligible
compared to the distances between them.
There are no attractive or repulsive forces between these
particles.
The particles are in constant rapid random motion, colliding with
each other and with the walls of the container.
The average kinetic energy of the particles is proportional to the
Kelvin temperature.
All collisions are perfectly elastic .

13. Ideal Gases versus Real Gases
• An ideal gas is one which obeys all the gas laws
and under all conditions of temperature and
pressure.
• No such gases exists, but real gases behave most
like an ideal gas at high temperatures and at low
pressures.
• Under these conditions, the particles of a real gas
are relatively far away from each other, and the
assumptions of the kinetic theory are reasonably
valid.

14. Why do real gases deviate?
• Intermolecular forces are present.
(Such as dipole – dipole, Van der Waals, etc.,)
• Molecules have volume.
• Collisions are not perfectly elastic.

15. Equation of State for an Ideal Gas
pV nRT
Measure
Pressure
Volume
Number of moles
Gas constant
Temperature
Conversions
Volume :
Temperature :
1L 1 10 3 m3
K
o
C 273
no. of mols:
n
actual mass
Mr
Symbol
p
V
n
R
T
Unit
Pa
m3
mol
JK 1mol
K
1

16. What volume will 24 g of O2 occupy at 20 o C and a pressure of 89000 Pa.
p 89000Pa
V ?
acutal mass
n
Mr
24
0.75 mols
32
R 8.3 J K 1 mol 1
T 20 273 293K
pV nRT
89000 V 0.75 8.3 293
0.75 8.3 293
V
89000
V 0.0204 m3

17. A student collected natural gas from a laboratory gas jet at 25o C in 0.25L flask until the pressure of the
gas was 73327.30 Pa. The gas sample weighted 0.118 g at a temperature of 25o C. From this data,
calculate the molecular mass of the gas.
p 73327.30Pa
V 0.25L 0.25 10 3 m3
n ?
R 8.3 J K 1 mol 1
T 25 273 298K
pV nRT
73327.30 0.25 10
3
73327.30 0.25 10
8.3 298
7.41 10 3 mol n
3
actual mass
n
0.118
mass
7.41 10 3
mass 15.92 g
Mr
n 8.3 298
n