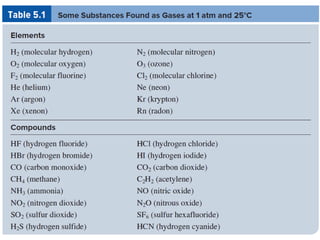
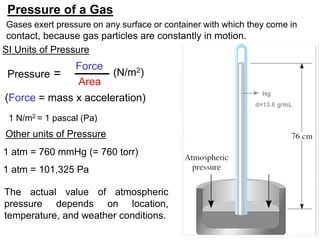
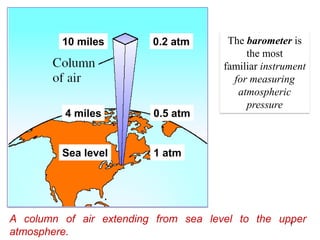
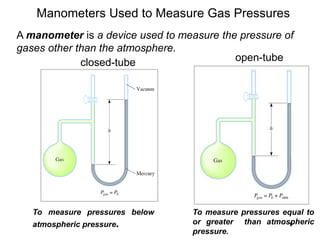
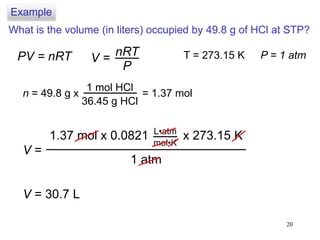
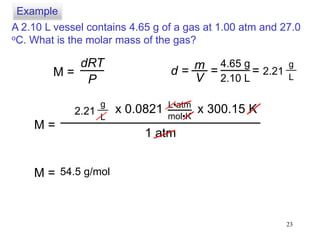
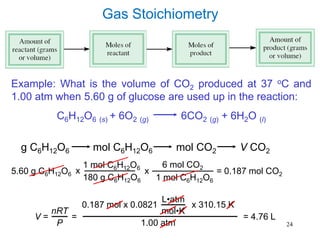
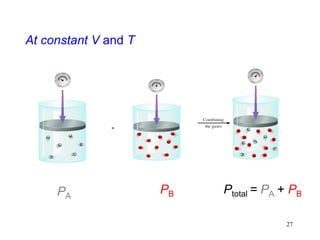
1. Gases have no definite shape or volume but take the shape of their container. Gas particles are in constant random motion and collide with each other and the container walls. 2. The kinetic molecular theory provides an explanation for gas behavior at the molecular level. It states that gas particles are in constant random motion and exert pressure due to collisions with container walls. 3. The gas laws describe the macroscopic behavior of gases through relationships between pressure, volume, temperature, and amount of gas. The kinetic molecular theory qualitatively explains the gas laws based on gas particle motion and interactions.

1. 1
Gases
Chapter 5
Dr. Sa’ib Khouri
AUM- JORDAN
Chemistry
By Raymond Chang

2. 2
Elements that exist as gases at 25 oC and 1 atmosphere

3. 3

4. 4
In the table
H2S and HCN are deadly poisons.
CO, NO2 , O3 , and SO2 , are somewhat
less toxic.
He, Ne, and Ar are chemically inert.
Most gases are colorless. Exceptions are
F2 , Cl2 , and NO2 .
O2 is essential for our survival.
The dark brown color of NO2 is sometimes visible in polluted air.

5. 5
1. Assume the volume and shape of their
containers.
All gases have the following physical
characteristics
2. Are the most compressible state of matter.
3. Will mix evenly and completely when
confined to the same container.
4. Have much lower densities than liquids and
solids.

6. 6
Other units of Pressure
1 atm = 760 mmHg (= 760 torr)
1 atm = 101,325 Pa
Pressure =
Force
Area
(Force = mass x acceleration)
Pressure of a Gas
SI Units of Pressure
(N/m2)
The actual value of atmospheric
pressure depends on location,
temperature, and weather conditions.
Gases exert pressure on any surface or container with which they come in
contact, because gas particles are constantly in motion.
1 N/m2 = 1 pascal (Pa)

7. 7
Sea level 1 atm
4 miles 0.5 atm
10 miles 0.2 atm
A column of air extending from sea level to the upper
atmosphere.
The barometer is
the most
familiar instrument
for measuring
atmospheric
pressure

8. 8
The pressure outside a jet plane flying at high altitude falls
considerably below standard atmospheric pressure. Therefore, the
air inside the cabin must be pressurized to protect the passengers.
What is the pressure in atmospheres in the cabin if the barometer
reading is 688 mmHg?
Example

9. 9
Manometers Used to Measure Gas Pressures
closed-tube open-tube
A manometer is a device used to measure the pressure of
gases other than the atmosphere.
To measure pressures below
atmospheric pressure.
To measure pressures equal to
or greater than atmospheric
pressure.

10. 10
P a 1/V
P x V = constant
P1 x V1 = P2 x V2
The Pressure-Volume Relationship: Boyle’s Law
Constant temperature
The Gas Laws
The pressure of a fixed amount of gas at a constant
temperature is inversely proportional to the volume of the gas.
Constant amount of gas

11. Increasing or decreasing the volume of a gas at a
constant temperature

12. 12
A sample of chlorine gas occupies a volume of 800 mL at a
pressure of 750 mmHg. What is the pressure of the gas (in
mmHg) if the volume is reduced at constant temperature to 200
mL?
P1 x V1 = P2 x V2
P1 = 750 mmHg
V1 = 800 mL
P2 = ?
V2 = 200 mL
P2 =
P1 x V1
V2
750 mmHg x 800 mL
200 mL
= = 3000 mmHg
P x V = constant
Example

13. 13
As T increases V increases
The Temperature-Volume Relationship:
Charles’ and Gay-Lussac’s Law

14. 14
V a T
V = constant x T
V1/T1 = V2 /T2
T (K) = t (oC) + 273.15
Temperature must be
in Kelvin (SI-unit)
When these lines
are extrapolated,
or extended, they
all intersect at the
point representing
zero volume and
a temperature of -
273.15 oC.

15. 15
A sample of carbon monoxide gas occupies 3.20 L at 398 K. At
what temperature will the gas occupy a volume of 1.54 L if the
pressure remains constant?
V1 = 3.20 L
T1 = 398 K
V2 = 1.54 L
T2 = ?
T2 =
V2 x T1
V1
1.54 L x 398 K
3.20 L
=
= 191.5 K
V1 /T1 = V2 /T2
Example

16. 16
V a number of moles (n)
V = constant x n
V1 / n1 = V2 / n2
Constant temperature
Constant pressure
At constant pressure and temperature, the volume of a gas is
directly proportional to the number of moles of the gas present
The Volume-Amount Relationship:
Avogadro’s Law

17. 17
The Ideal Gas Equation
Charles’ law: V a T (at constant n and P)
Avogadro’s law: V a n (at constant P and T)
Boyle’s law: V a (at constant n and T)1
P
V a
nT
P
V = constant x = R
nT
P
nT
P
R is the gas constant
PV = nRT
Combination of all three expressions:
Ideal gas equation

18. 18
At 0°C (273.15 K) and 1 atm pressure (standard temperature
and pressure (STP)), many real gases behave like an ideal.
PV = nRT R =
PV
nT
=
(1 atm)(22.414L)
(1 mol)(273.15 K)
R = 0.082057 L • atm / mol • K
Experiments show that at STP, 1 mole of an ideal gas occupies
22.414 L.
Ideal gas: a hypothetical gas whose molecules occupy negligible
space compared with the volume of the container and have no
interactions.
For most calculations:
R = 0.0821 L • atm / mol • K

19. 19
A certain light bulb containing argon at 1.20 atm and
18 oC is heated to 85 oC at constant volume. What
is the final pressure of argon in the light bulb (in
atm)?
PV = nRT n, V and R are constant
nR
V
=
P
T
= constant
P1
T1
P2
T2
=
P1 = 1.20 atm
T1 = 291 K
P2 = ?
T2 = 358 K
P2 = P1 x
T2
T1
= 1.20 atm x 358 K
291 K
= 1.48 atm
Example

20. 20
What is the volume (in liters) occupied by 49.8 g of HCl at STP?
PV = nRT V =
nRT
P
T = 273.15 K P = 1 atm
n = 49.8 g x
1 mol HCl
36.45 g HCl
= 1.37 mol
V =
1 atm
1.37 mol x 0.0821 x 273.15 KL•atm
mol•K
V = 30.7 L
Example

21. 21
Hint. Assume the amount of gas in the bubble remains constant

22. 22
Density and Molar Mass Calculations
d =
PM
R T
m: the mass of the gas in g
M: the molar mass of the gas in g/mol
dRT
P
M =
d: is the density of the gas in g/L
(n=
m
M
)PV = n RT → PV =
m
M
RT
or PM =
m
V
RT
PM = d RT
m
V
= d
PM= dRT →

23. 23
A 2.10 L vessel contains 4.65 g of a gas at 1.00 atm and 27.0
oC. What is the molar mass of the gas?
dRT
P
M = d = m
V
4.65 g
2.10 L
= = 2.21
g
L
M =
2.21
g
L
1 atm
x 0.0821 x 300.15 KL•atm
mol•K
M = 54.5 g/mol
Example

24. 24
Gas Stoichiometry
Example: What is the volume of CO2 produced at 37 oC and
1.00 atm when 5.60 g of glucose are used up in the reaction:
C6H12O6 (s) + 6O2 (g) 6CO2 (g) + 6H2O (l)
g C6H12O6 mol C6H12O6 mol CO2 V CO2
5.60 g C6H12O6
1 mol C6H12O6
180 g C6H12O6
x
6 mol CO2
1 mol C6H12O6
x = 0.187 mol CO2
V =
nRT
P
0.187 mol x 0.0821 x 310.15 K
L•atm
mol•K
1.00 atm
= = 4.76 L

26. • According to the kinetic molecular theory, the gas
particles in a mixture behave independently, i.e.
each gas exerts a pressure independent of the
other gases in the mixture.
• All gases in the mixture have the same volume and
temperature.
• The pressure of a component gas in a mixture is
called a partial pressure.
• The sum of the partial pressures of all the gases in
a mixture equals the total pressure.
Dalton’s Law of Partial Pressures

27. 27
At constant V and T
PA
PB Ptotal = PA + PB

28. 28
Consider a case in which two gases, A and B, are in a
container of volume V.
PA =
nART
V
PB =
nBRT
V
nA is the number of moles of A
nB is the number of moles of B
PT = PA + PB
PA = XA PT
PB = XB PT
Pi = Xi PT mole fraction (Xi ) =
ni
nT

29. 29
Pi = Xi PT PT = 2.00 atm

30. 30
Collecting Gases
• Gases are often collected by having them displace
water from a container.
• The problem is that since water evaporates, there is
also water vapor in the collected gas.
• The partial pressure of the water vapor, called the
vapor pressure, depends only on the temperature. So
you can use a table to find out the partial pressure of
the water vapor in the gas you collect.
• If you collect a gas sample with a total pressure of
758 mmHg at 25 °C, the partial pressure of the
water vapor will be 23.8 mmHg, so the partial
pressure of the dry gas will be 734 mmHg
(Dalton’s law )

31. 31
Vapor of Water and Temperature

32. 32
2KClO3 (s) 2KCl (s) + 3O2 (g) PT = PO2
+ PH2O
Example

34. 34
The gas laws help us to predict the behavior of gases, but they do not explain what
happens at the molecular level to cause the changes observed in the macroscopic
world. e.g. why does a gas expand on heating?
The Kinetic Molecular Theory of Gases
In the 19th century, L. Boltzmann and J.C. Maxwell, found that the physical
properties of gases can be explained in terms of the motion of individual
molecules. This molecular movement is a form of energy, which can be defined as
the capacity to do work or to produce change.
Work is defined as force times distance (Work = force × distance)
The findings of Maxwell, Boltzmann, and others resulted in a number of
generalizations about gas behavior that have since been known as the kinetic
molecular theory of gases, or simply the kinetic theory of gases

35. 35
Assumptions
1. A gas is composed of molecules (or atoms) that are separated from each
other by distances far greater than their own dimensions. The molecules can
be considered to be “points”; that is, they possess mass but have negligible
volume.
2. Gas molecules are in constant motion in random directions, and they
frequently collide with one another. Collisions among molecules are perfectly
elastic. In other words, energy can be transferred from one molecule to
another as a result of a collision. Nevertheless, the total energy of all the
molecules in a system remains the same.
3. Gas molecules exert neither attractive nor repulsive forces on one
another.

36. 36
4.The average kinetic energy of the molecules is proportional to the
temperature of the gas in kelvins. Any two gases at the same temperature
will have the same average kinetic energy. The average kinetic energy of a
molecule is given by
KE = ½ mu2
where m is the mass of the molecule and u is its speed, The horizontal bar
denotes an average value. The quantity u2 (bar) is called mean square
speed; it is the average of the square of the speeds of all the molecules:
where N is the number of molecules.
Assumption 4 enables us to write
where C is the proportionality constant and T is the absolute temperature

37. 37
According to the kinetic molecular theory, gas pressure is the result of
collisions between molecules and the walls of their container. It depends
on the frequency of collision per unit area and on how “hard” the molecules
strike the wall.
The theory also provides a molecular interpretation of temperature. The
absolute temperature is an indication of the random motion of the
molecules, the higher the temperature, the more energetic the molecules
Because it is related to the temperature of the gas sample, random
molecular motion is sometimes referred to as thermal motion.

38. 38
Application to the Gas Laws
• Compressibility of Gases:
Because molecules in the gas phase are separated by large distances
gases can be compressed easily to occupy less volume.
• Boyle’s Law
P a collision rate with wall
Collision rate a number density (per unit volume)
Number density a 1/V
P a 1/V
Although the kinetic theory of gases is based on a rather simple model, the
mathematical details involved are very complex. However, on a qualitative basis, it
is possible to use the theory to account for the general properties of substances in
the gaseous state. The following examples illustrate the range of its utility.

39. 39
• Avogadro’s Law
P a collision rate with wall
Collision rate a number density
Number density a n
P a n
• Dalton’s Law of Partial Pressures
Molecules do not attract or repel one another
P exerted by one type of molecule is unaffected by the
presence of another gas
Ptotal = SPi
• Charles’ Law
P a collision rate with wall, which comes from raising T.
Collision rate a average kinetic energy of gas molecules
Average kinetic energy a T
P a T

40. 40
The distribution of speeds for
nitrogen gas molecules at
three different temperatures
The distribution of speeds
of three different gases at
the same temperature
Distribution of Molecular Speeds
Maxwell analyzed the behavior of gas molecules at different temperatures.

41. 41

42. 42
Gas Diffusion and Effusion
Two phenomena based on gaseous motion
Gas Diffusion
The gradual mixing of molecules of one gas with molecules of another by
virtue of their kinetic properties
The diffusion process takes a relatively long time to complete.
For example, when a bottle of concentrated ammonia solution is opened at one end of a
lab bench, it takes some time before a person at the other end of the bench can smell it,
due to numerous collisions.
The path travelled by a single gas molecule. Each
change in direction represents a collision with
another molecule.
Because NH3 is lighter and therefore diffuses faster, solid
NH4Cl first appears nearer the HCl bottle.
A lighter gas will diffuse more quickly than will a heavier gas

43. 43
r1
r2
M2
M1=
Thomas Graham: under the same conditions of temperature and pressure, rates of
diffusion for gases are inversely proportional to the square roots of their molar
masses (Graham’s law of diffusion)
r1 and r2 are the diffusion rates of gases 1 and 2,
ℳ1 and ℳ2 are their molar masses.
Gas Effusion
The process by which gas under pressure escapes from one compartment
of a container to another by passing through a small opening
Gas effusion.
Gas molecules move from a high-pressure region (left) to a
low-pressure one through a pinhole.

44. 44
=
r1
r2
t2
t1
M2
M1=
e.g. Nickel forms a gaseous compound of the formula Ni(CO)x. What is the
value of x given that under the same conditions methane (CH4) effuses 3.3
times faster than the compound?
r1 = 3.3 x r2
M1 = 16 g/mol
M2 =
r1
r2
( )
2
x M1 = (3.3)2 x 16 = 174.2
58.7 + x • 28 = 174.2 x = 4.1 ~ 4
The rate of effusion of a gas has the same form as Graham’s law of diffusion
Industrially, gas effusion is used to separate uranium isotopes in the forms of gaseous
235UF6 and 238UF6, which was used in the construction of atomic bombs.
Practice Exercise It takes 192 s for an unknown gas to effuse through a porous wall
and 84 s for the same volume of N2 gas to effuse at the same temperature and
pressure. What is the molar mass of the unknown gas?

45. 45
Deviation from Ideal Behavior
Plot of
PV/RT
versus
P of 1
mole of
a gas
at 0°C
For 1 mole of an ideal gas,
PV/RT is equal to 1, no matter
what the pressure of the gas is.
For real gases, we observe
various deviations from ideality at
high pressures.
At very low pressures, all gases exhibit ideal behavior; that is, their
PV/RT values all converge to 1 as P approaches zero.
At atmospheric pressure, the molecules in a gas are far apart and the attractive
forces are negligible. At high pressures, the density of the gas increases; the
molecules are much closer to one another. Intermolecular forces can then be
significant enough to affect the motion of the molecules, and the gas will not
behave ideally.

46. 46
Van der Waals equation
nonideal gas
P + (V – nb) = nRTan2
V2( )
}
corrected
pressure
}corrected
volume
The value of a indicates how strongly
molecules of a given type of gas attract
one another.
There is also a correlation between
molecular size and b. The larger the
gas particle the greater b is.

49. H.W.
Using the van der Waals equation, calculate the pressure exerted
by 15.0 mol of carbon dioxide confined to a 3.0 L vessel at 329 K.
Note: Values for a and b in the van der Waals equation:
a = 3.59 L
2
.atm/mol
2
, b = 0.0427 L/mol.
A) 23.2 atm
B) 2.16 atm
C) 81.9 atm
D) 96.4 atm