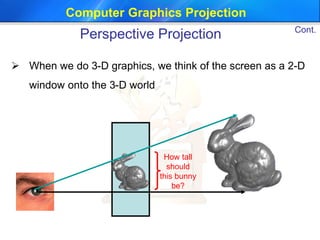
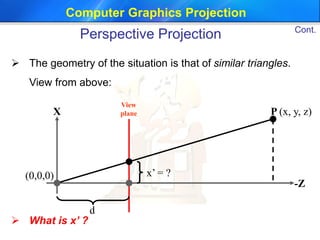
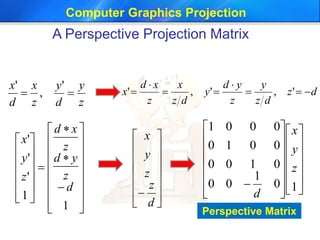
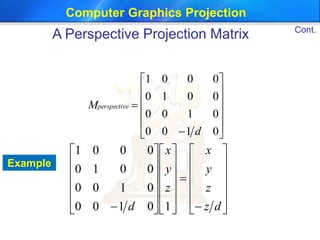
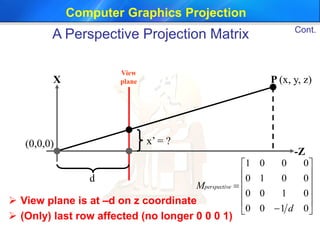
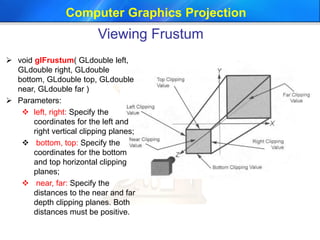
This document discusses different types of projections used in computer graphics, including perspective and parallel projections. It describes orthographic projection, which projects points along the z-axis onto the z=0 plane. Perspective projection is also covered, including how it creates the effect of objects appearing smaller with distance using similar triangles. The document provides the equation for a perspective projection matrix and an example. It concludes by discussing defining a viewing region or frustum using functions like glFrustum and gluPerspective in OpenGL.

1. SBE 306: Computer Graphics
Projection
Dr. Ayman Eldeib
Systems & Biomedical
Engineering Department
Spring 2019

2. Computer Graphics Projection
Types of Projections
Perspective
Projection
Parallel
Projection
“Orthographic ”

3. Computer Graphics Projection
Simple Orthographic Projection
 Project all points along the z axis to the z= 0 plane





































11000
0000
0010
0001
1
0
'
'
z
y
x
y
x

4. Computer Graphics Projection
Perspective Transformations
 Perspective transformations do not preserve parallelism,
i.e. Parallel lines not parallel; converge to single point
 Further objects are smaller (size, inverse distance)
B
A’
B’
Center of projection
(camera/eye location)
A

5. Computer Graphics Projection
Perspective Projection
 In the real world, objects exhibit perspective
foreshortening: distant objects appear smaller.
 The basic situation:

6. Computer Graphics Projection
 When we do 3-D graphics, we think of the screen as a 2-D
window onto the 3-D world
How tall
should
this bunny
be?
Cont.
Perspective Projection

7. Computer Graphics Projection
 The geometry of the situation is that of similar triangles.
View from above:
P (x, y, z)X
-Z
View
plane
d
(0,0,0) x’ = ?
 What is x’ ?
Cont.
Perspective Projection

8. Computer Graphics Projection
P (x, y, z)X
-Z
View
plane
d
(0,0,0) x’ = ?
z
y
d
y
z
x
d
x

'
,
'
dz
dz
y
z
yd
y
dz
x
z
xd
x 



 ',','
Cont.
Perspective Projection

9. Computer Graphics Projection
A Perspective Projection Matrix
z
y
d
y
z
x
d
x

'
,
'
dz
dz
y
z
yd
y
dz
x
z
xd
x 



 ',','















d
z
z
y
x
































1
1
'
'
'
d
z
yd
z
xd
z
y
x


























 10
1
00
0100
0010
0001
z
y
x
d
Perspective Matrix

10. Computer Graphics Projection
Example














0100
0100
0010
0001
d
M eperspectiv






































 dz
z
y
x
z
y
x
d 10100
0100
0010
0001
Cont.
A Perspective Projection Matrix

11. Computer Graphics Projection
P (x, y, z)X
-Z
View
plane
d
(0,0,0) x’ = ?














0100
0100
0010
0001
d
M eperspectiv
 View plane is at –d on z coordinate
 (Only) last row affected (no longer 0 0 0 1)
Cont.
A Perspective Projection Matrix

12. Computer Graphics Projection
 Now that we can express perspective
foreshortening as a matrix, we can composite it
onto our other matrices with the usual matrix
multiplication
 End result: can create a single matrix
encapsulating modeling, viewing, and projection
transforms
Though you recall that in practice OpenGL
separates the modelview from projection
matrix (why?)
Cont.
A Perspective Projection Matrix

13. Computer Graphics Projection
Defining a Viewing Region
 Most graphics API’s use two methods for defining a
viewing region
 The viewing frustum
In OpenGL glFrustum (xmin,xmax,ymin,ymax,near,far)
 The screen projection plane
This is a special case of the viewing frustum
Also called the symmetric perspective projection frustum
In OpenGL gluPerspective (theta,aspect,near,far)

14. Computer Graphics Projection
Viewing Frustum
 void glFrustum( GLdouble left,
GLdouble right, GLdouble
bottom, GLdouble top, GLdouble
near, GLdouble far )
 Parameters:
 left, right: Specify the
coordinates for the left and
right vertical clipping planes;
 bottom, top: Specify the
coordinates for the bottom
and top horizontal clipping
planes;
 near, far: Specify the
distances to the near and far
depth clipping planes. Both
distances must be positive.

15. Computer Graphics Projection
 void gluPerspective( GLdouble fovy,
GLdouble aspect, GLdouble zNear,
GLdouble zFar )
 Parameters:
 Fovy: Specifies the field of view
angle, in degrees, in the y
direction;
 Aspect: Specifies the aspect ratio
that determines the field of view in
the x direction. The aspect ratio is
the ratio of x (width) to y (height);
 ZNear: Specifies the distance from
the viewer to the near clipping
plane (always positive);
 ZFar: Specifies the distance from
the viewer to the far clipping plane
(always positive)
Cont.
Viewing Frustum

16. Computer Graphics Projection
 The viewing frustum defines a region of 3D space
assuming that the eye is located at (0, 0, 0).
 A 4x4 perspective transformation maps the
viewing frustum to a canonical cube
 Once a canonical cube is obtained 3D points are
projected to 2D by dropping the z component
 Note perspective projection is obtained by using
a perspective transformation followed by
orthographic projection
Cont.
Viewing Frustum

17. Computer Graphics Projection
 OpenGL’s gluPerspective() command generates a
slightly more complicated matrix:














































2
cotwhere
0100
2
00
000
000
y
farnear
nearfar
farnear
nearfar
fov
f
ZZ
ZZ
ZZ
ZΖ
f
aspect
f
Cont.
Viewing Frustum

18. Thank You