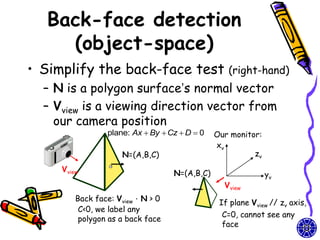
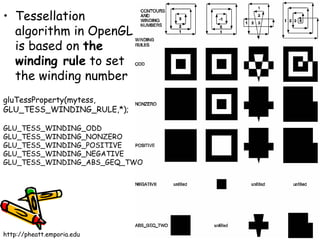
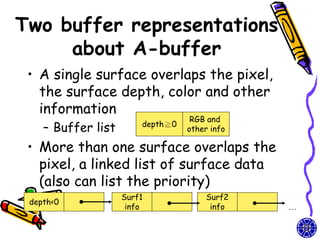
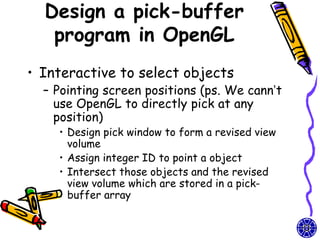
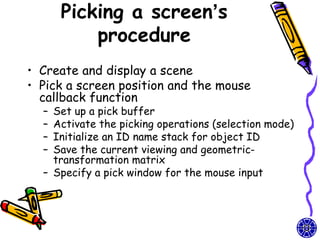
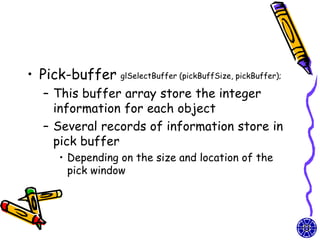
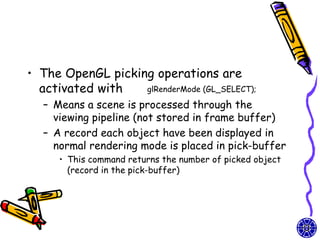
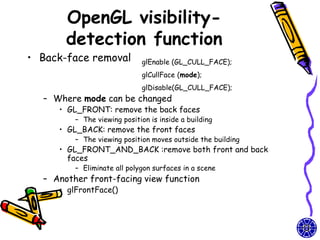
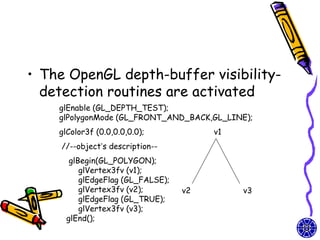
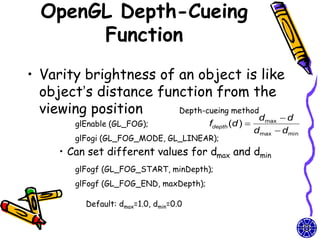
The document discusses methods for visible-surface detection in computer graphics, including back-face detection and removal, depth-buffer techniques, and image-space versus object-space approaches. It also covers illumination models, such as ambient and diffuse reflections, along with rendering methods in OpenGL for polygon rendering. Additionally, it touches on techniques like tessellation and design considerations for interactive object selection using a pick-buffer.

1. Visible-surface detection
Methods + Illumination
Models & surface-
rendering models
Chen Jing-Fung (2006/12/8)
Assistant Research Fellow,
Digital Media Center,
National Taiwan Normal University
Ch9: Computer Graphics with OpenGL 3th, Hearn Baker
Ch11-6: Computer Graphics with OpenGL 3th, Hearn Baker
Ch10: Computer Graphics with OpenGL 3th, Hearn Baker

2. Visible-surface
• Visible-surface detection
– Polygon’s vertices & plane have some
relationship
– Back-face detection
– Back-face removals
– Concave Polygons
– Depth-Buffer method

3. Visible-surface
detection
• How to describe the surface?
– Object-space
• Compare objects or parts of objects in the scene
– We should label as visible
– Advantage: effectively locate visible surfaces in the
same case
– Image-space
• Visibility is decided each pixel position’s point (the
closest to viewer) on the projection plane
• Most interface is only image-space

4. Object- & Image-
space
• The major differences is in the basic
approaches about the various visible-
surface detection algorithms
– Sorting method
• Based on facilitate depth (interval distance)
which used to divide surfaces in a scene
– Coherence method
• Using the regularities in a scene

5. Polygon’s vertices & plane
plane: Ax  By  Cz  D  0
• Using three points resolve a
plane (x1,y1,z1)
NPlane
any plane function: Ax  By  Cz  D  0 (x ,y ,z )
2 2 2
(x3,y3,z3)
– Each intercept between the plane
and the axis
• x-axis: A/D, y-axis: B/D, z-axis: C/D
 (A / D)xk  (B / D)y k  (C / D)zk  1 k=1,2,3
,
Cramer’s rule: 1 y1 z1 x1 1 z1 x1 y1 1
A  1 y 2 z2 B  x2 1 z2 C  x2 y 2 1
1 y3 z3 x3 1 z3 x3 y3 1
x1 y1 z1
D   x2 y2 z2
x3 y3 z3

6. Back-face detection
(object-space)
• Simplify the back-face test (right-hand)
– N is a polygon surface’s normal vector
– Vview is a viewing direction vector from
our camera position
plane: Ax  By  Cz  D  0 Our monitor:
xv
N=(A,B,C) zv
Vview N=(A,B,C) yv
Vview
Back face: Vview．N > 0 If plane Vview // zv axis,
C<0, we label any
C=0, cannot see any
polygon as a back face
face

7. Back-face removals
• In general, back-face removal can
eliminate about partly or completely
of polygon surfaces
– Convex surface: C 0 C=0, cannot see any face
• All hidden surfaces C < 0, we label any
polygon as a back face
– C>0 C > 0, hidden surface
C0
– Concave surface:
• Like to combine two convex objects
One face is be partially hidden by
other faces of the object

8. OpenGL and Concave
Polygons
• A tessellator object in the GLU
library can tessellate a given polygon
into flat convex polygons
– Draw a simple polygon without holes
• basic idea is to describe a contour
mytess = gluNewTess(); //include
gluTessProperty()
gluTessBeginPolygon(mytess, NULL); //send them off to be rendered
gluTessBeginContour(mytess);// draw contour (outside)
for(i=0; i < n_vertices; i++)
glTessVertex(mytess,vertex[i],vertex[i]);
gluTessEndContour();
gluTessEndPolygon(mytess);

9. • Tessellation
algorithm in OpenGL
is based on the
winding rule to set
the winding number
gluTessProperty(mytess,
GLU_TESS_WINDING_RULE,*);
GLU_TESS_WINDING_ODD
GLU_TESS_WINDING_NONZERO
GLU_TESS_WINDING_POSITIVE
GLU_TESS_WINDING_NEGATIVE
GLU_TESS_WINDING_ABS_GEQ_TWO
http://pheatt.emporia.edu

10. Depth-Buffer method
• A common image-space approach for
detecting visible surfaces is depth-
buffer method
– One pixel position at a time appear to
the surface
– Also called to z-buffer method
• Object depth is usually measured along z
axis of a viewing system

11. Depth buffer
• Three surfaces and view plane
overlap pixel position (x,y) on the
view plane
– The visible surface has the smallest
depth value  P Py aP  b  pseudodepth
( x, y, z )   x , , z 
P P P 
 z z z 
View plane
Depthvalue = 1.0 yv
-> far (x,y)
xv
Depthvalue=0.0
-> near zv

12. Possible data type to
hold face data
Class face{
int nVerts; //number of vertices in vertex-array
Point *pt; //array of vertices in real screen coord’s
float *depth; //array of vertex depths
Plane plane; //data for the plane of the face
Exface extent; //the extent of the face
//other properties
};
Ch13: Computer Graphics 2th, F. S. Hill Jr.

13. Depth-Buffer Algorithm
• Initialize the depth buffer and frame
buffer so that for all buffer positions (x,y)
depthBuff (x,y) = 1.0, frameBuff (x,y) = backgndColor
• Process each polygon in a scene, one at a
time
– For each projected (x,y) pixel position of a
polygon, calculate the depth z (if not allready
known)
– If z < depthBuff(x,y), compute the surface
color at that position and set
depthBuff (x,y) = z, frameBuff (x,y) = surfColor(x,y)

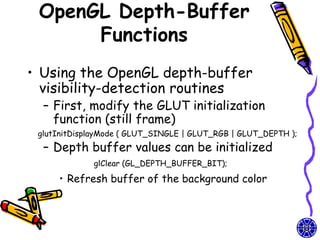
14. Basic flow of depth-
buffer algorithm
• pseudocode
for (each face F)
for (each pixel (x,y) covering the face){
depth = depth of F at (x,y);
if (depth < d[x][y]) { //F is closest so far
c = color of F at (x,y) //set the pixel color at (x,y) to c
d[x][y] = depth; //updata the depth buffer
}
}

15. A-Buffer Method
• Extension of above depth-buffer ideas is
A-Buffer procedure
– Combined with antialiasing, area-averaging and
visiblity-detection method
– Developed at Lucasfilm Studios to include in
the surface-rendering system called REYES
(Renders Everything You Ever Saw)
– The buffer region is referred to as the
accumulation buffer
• Store a variety of surface data and depth values

16. Two fields in A-buffer
method
• Each position in the A-buffer has two
fields:
– Depth field
• Stores a real-number value (+,- or 0)
– Surface data field
• Stores surface data or a pointer

17. Two buffer representations
about A-buffer
• A single surface overlaps the pixel,
the surface depth, color and other
information
RGB and
– Buffer list depth≧0
other info
• More than one surface overlaps the
pixel, a linked list of surface data
(also can list the priority)
Surf1 Surf2
depth<0
info info …

18. A-buffer
• Summary the surface information in A-
buffer
– RGB intensity components
– Opacity parameter (percent of transparency)
– Depth
– Percent of area coverage
– Surface identifier
– Other surface-rendering parameters

19. Design a pick-buffer
program in OpenGL
• Interactive to select objects
– Pointing screen positions (ps. We cann’t
use OpenGL to directly pick at any
position)
• Design pick window to form a revised view
volume
• Assign integer ID to point a object
• Intersect those objects and the revised
view volume which are stored in a pick-
buffer array

20. Picking a screen’s
procedure
• Create and display a scene
• Pick a screen position and the mouse
callback function
– Set up a pick buffer
– Activate the picking operations (selection mode)
– Initialize an ID name stack for object ID
– Save the current viewing and geometric-
transformation matrix
– Specify a pick window for the mouse input

21. – Assign identifiers to objects and reprocess the
screen using revised view volumne. (pick
information is stored in pick buffer)
– Restore the original viewing and geometric-
transformation matrix
– Determine the number of objects that have
been picked and return to the normal rendering
mode
– Process the pick information

22. • Pick-buffer glSelectBuffer (pickBuffSize, pickBuffer);
– This buffer array store the integer
information for each object
– Several records of information store in
pick buffer
• Depending on the size and location of the
pick window

23. Each record in pick-
buffer’s information
• The stack position of the object which is
the number of identifiers in the name
stack up to and including the position of
the picked object
• Min depth of the picked object
• Max depth of the same object
• The list of the identifies in the name stack
from the first (bottom) identifier to the
identifier for the picked object
Range = 0.0~1.0 multiplied by 232-1

24. • The OpenGL picking operations are
activated with glRenderMode (GL_SELECT);
– Means a scene is processed through the
viewing pipeline (not stored in frame buffer)
– A record each object have been displayed in
normal rendering mode is placed in pick-buffer
• This command returns the number of picked object
(record in the pick-buffer)

25. After mouse hit
• To return to the normal rendering
mode (the default)
glRenderMode (GL_RENDER);
• third option (GL_FEEDBACK)
– Store object coordinates without
displaying

26. Buffer depth test demo

27. OpenGL visibility-
detection function
• Back-face removal glEnable (GL_CULL_FACE);
glCullFace (mode);
glDisable(GL_CULL_FACE);
– Where mode can be changed
• GL_FRONT: remove the back faces
– The viewing position is inside a building
• GL_BACK: remove the front faces
– The viewing position moves outside the building
• GL_FRONT_AND_BACK :remove both front and back
faces
– Eliminate all polygon surfaces in a scene
– Another front-facing view function
• glFrontFace()

28. OpenGL Depth-Buffer
Functions
• Using the OpenGL depth-buffer
visibility-detection routines
– First, modify the GLUT initialization
function (still frame)
glutInitDisplayMode ( GLUT_SINGLE | GLUT_RGB | GLUT_DEPTH );
– Depth buffer values can be initialized
glClear (GL_DEPTH_BUFFER_BIT);
• Refresh buffer of the background color

29. • The OpenGL depth-buffer visibility-
detection routines are activated
glEnable (GL_DEPTH_TEST);
glPolygonMode (GL_FRONT_AND_BACK,GL_LINE);
glColor3f (0.0,0.0,0.0); v1
//--object’s description--
glBegin(GL_POLYGON);
glVertex3fv (v1);
glEdgeFlag (GL_FALSE);
glVertex3fv (v2); v2 v3
glEdgeFlag (GL_TRUE);
glVertex3fv (v3);
glEnd();

30. • The depth-buffer visibility testing use
other initial value for the max-depth
glClearDepth (maxDepth);
glClear(GL_DEPTH_BUFFER_BIT);
– The depth buffer is initialized with the default
value 1.0 (maximum depth-buffer in OpenGL)
– This function can be used to speed up the
depth-buffer routines
• That is like many distant objects behind the
foreground objects
minimum depth-buffer in OpenGL = 0.0

31. Projection application
• Projection coordinates in OpenGL
– normalize the range -1.0~1.0
– The depth values between near and far are
normalized to the range 0.0~1.0
• Default: Near: 0.0; far:1.0
glDepthRange (nearnormdepth, farnormdepth)
– Any value can be set
including nearnormdepth>farnormdepth

32. Other option about
depth-buffer in OpenGL
glDepthFunc (testCondition);
– Parameter testCondition can be assigned
8 symbolic constants
• GL_LESS (default), GL_GREATER,
GL_EQUAL, GL_NOTEQUAL, GL_LEQUAL,
GL_GEQUAL, GL_NEVER (no point),
GL_ALWAYS (all points).
– They are used to compare each incoming pixel z
value with present z value in the depth-buffer
– GL_LESS: the depth-value is less than current
value in the depth-buffer

33. Set the depth-buffer
state
• Set the state of the depth-buffer to
read-only or read-write
glDepthMask (writeState);
– writeState = GL_TRUE (default): read-
write
– writeState = GL_FALSE: only can
retrieve values

34. The advantage of the
setting state
• The feature is useful in complicated
background v.s. different foreground
objects can be displayed
– Disable the background write mode and
process foreground
• Allow to generate a series of frames with different
foreground objects
• Or one object in different positions for an animation
sequence.
• Therefore, only depth values for the background are
saved

35. OpenGL Depth-Cueing
Function
• Varity brightness of an object is like
object’s distance function from the
viewing position Depth-cueing method
dmax  d
glEnable (GL_FOG); fdepth (d ) 
dmax  dmin
glFogi (GL_FOG_MODE, GL_LINEAR);
• Can set different values for dmax and dmin
glFogf (GL_FOG_START, minDepth);
glFogf (GL_FOG_END, maxDepth);
Default: dmax=1.0, dmin=0.0

36. Approaches to infinity
• There are many complex pictures
which could be compose to the simple
component
– Tesselations could based on a single
regular polygon
• Only a triangle, square and hexagon tile the
plane

37. Drawing simple
tesselations
• Consider how to draw in an application the
3-gon tillings
– The 3-gon version
• Row : draw those side-by-side equilateral triangles
which are all the same orientation
• Other row must be offset horizontally by ½ the base
of the triangle (each line is drawn only once)
• Clipping can be used to chop off the tilings at the
borders of the desired window

38. Drawing simple
tesselations
• Code fragment
for i=1~ rowsnum
for j=1 ~ colsnum
if i=Odd
offset+=shift
else offset = 0
Triangle (j*colWidth+offset, i*rowWidth, 1);

39. Illumination Models &
surface-rendering models
Ch10: Computer Graphics with OpenGL 3th, Hearn Baker

40. outline
• Basic illumination models
• Polygon rendering methods
• OpenGL lights
40

41. Basic illumination models
• Ambient light
• Diffuse reflection
• Specular reflection
• Combine diffuse & specular
reflection
• Light refraction
41

42. Ambient light
• Ambient light set a general brightness
level in a scene
– object combine all background lighting ~ the
global diffuse reflections
• Assuming that only monochromatic lighting
– Intensity parameter Ia
– Ambient light’s reflections
• a simply form of diffuse reflection
• Independent of viewing direction & spatial
orientation of a surface
42

43. Diffuse reflection (1)
• Diffuse reflection model
– Assume the incident light is scattered
with equal intensity in all directions
(ideal diffuse reflectors)
• the reflected radiant light energy is
calculated with Lambert’s cosine law
radiant energy per unit time
Intensity 
projected area
cos N
~  constant
dA cos N
43

44. Diffuse reflection (2)
• Radiant energy from a surface area
element dA in direction ψN relative to
the surface normal direction is
proportional to cos ψN
– a monochromatic light source, kd:0.0~1.0
N
ψN Incident light Highly reflective surface kd=1.0
ψN
dA Radiant-energy
direction
Absorbs the incident light kd=0.0
44

45. Lighting & reflection (1)
• Background lighting effects
– Every surface is fully illuminated by the
ambient light Ia
– Ambient lighting contribution to the
diffuse reflection at any point
– Produces a abnormally flat shading
Iambdiff=kdIa kd:0.0~1.0
abnormally flat shading
…
45

46. Lighting & reflection (2)
• Modeling the amount of incident light
(Il,incident) on a surface (A) from a
light source with intensity (Il)
Il,incident=Il cosθ
• The diffuse reflections N
θ
A
Incident
light θ A cosθ
Il,diff=kdIl,incident=kdIl cosθ
Incoming light ⊥ the surface => θ= 0°, Il,diffuse=kdIl
cosθ≦0.0, light source is behind the surface
46

47.  kd Il (N  L), if N  L  0
Il ,diff 
 0.0, if N  L  0 N
L
θ
Psource  Psurf To light cosθ=N．L
L source
Psource  Psurf
• Diffuse reflections from a spherical surface
• Point light source color = white
• Diffuse reflectivity coefficient : 0 <= kd <= 1
47

48. kaIa  kd Il (N  L), if N  L  0
Idiff 
 k a Ia , if N  L  0
• Combine the
ambient & point-
source intensity
calculations the
total diffuse
reflection
– Ambient-
reflection
coefficient ka
48

49. Specular reflection
49
http://accad.osu.edu/~waynec/history/tree/images/turner.jpg

50. • The specular reflection direction for
a position on an illuminated surface
N R
L θ θ
φ V
N: normal surface vector
R: ideal specular reflection Rs
L: the direction toward the point light source
V: point to viewer
An ideal reflector (perfect mirror)
Il,incident = Rs &
we would see reflected light when V and R coincide
50

51. Specular-refection
function
• The variation of specular intensity with
angle of incidence is described by
Fresnel’s laws of reflection N
L θ θR
Il ,spec  W ( )Il cos 
ns
φ V
– Spectral-reflection function W(θ)
– The intensity of the light source Il
– φ: between the viewing angle (V) and R
51

52. cos 
ns
52

53. Specular-reflection
coefficient
• Approximate variation of the
specular-reflection coefficient
for different materials, as a
function of the angle of
incidence
– W(θ): 0.0~1.0
– In general, W(θ) tends to
increase (θ=0°->90°°)
– θ=90°, W(θ)=1
• All of the incidence is reflected
Ex: glass,
-θ=0°->4% of the incident light on a
glass surface
-and most of the rangeθ-> < 10%
53

54. Simple specular- θ
reflection function (1) θ
• Many opaque materials’ specular-
reflection is nearly constant
– Set ks=W(θ), ks:0.0~1.0
ksIl ( V  R )ns , if V  R  0 and N  L  0
Il ,spec 
 0.0, if V  R  0 or N  L  0
– R? can be computed from L and N
R + L = (2N．L) N
=> R = (2N．L) N - L
54

55. Simple specular-
reflection function (2)
H
• We replace V．R with N．H L
Nα R
φ V
– Replace cosφ with cosα
LV
Halfway vector H
LV
– Advantage
• For nonplanar surfaces, N．H requires less
computation than V．R because R related with N
– Viewer and light source is sufficiently far
• V, L and H are all constant
If α > 90°, N．H = negative and set Il,spec=0.0
55

56. ksIl (N  H)ns , if N  H  0
Il ,spec 
 0.0, if N  H  0
56

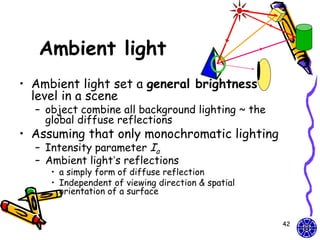
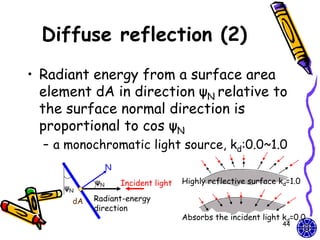
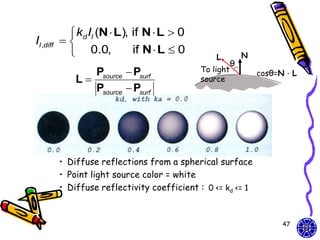
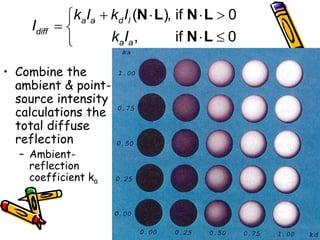
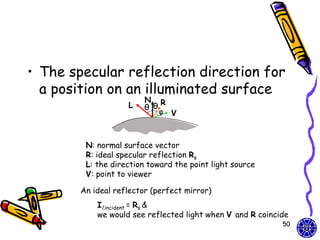
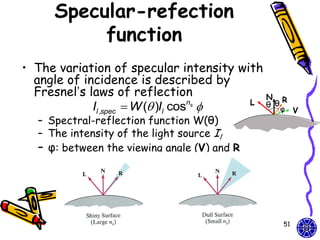
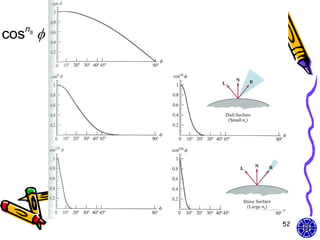
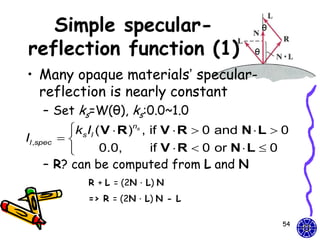
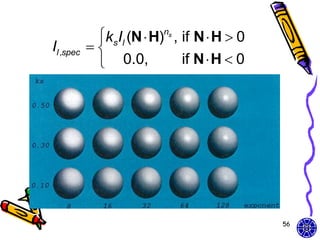
57. Combined diffuse and
specular reflection
• A single point light source
I  Idiff  Ispec
 kaIa  kd Il (N  L)  ksIl (N  H)ns
• Multiple light sources
n
I  Iambdiff   [Il ,diff  Il ,spec ]
l 1
n
 kaIa   Il [kd (N  Ll )  ks (N  Hl )ns ]
l 1
57

58. Wire-frame Ambient lighting
Diffuse reflections from ambient Diffuse and specular reflections from
lighting + a single point source ambient lighting + a single point source
58

59. Light refraction (1)
59

60. Light refraction (2)
• Snell’s law
i
sin r  sin i
r
– Different material
have different
refracted
coefficience ηair~ 1
(ηmaterial)
ηglass~ 1.61
60

61. Polygon rendering
methods
• Flat surface rendering
• Gouraud surface rendering
• Phong surface rendering
61

62. Flat surface rendering
• Flat surface rendering is also called
constant-intensity surface rendering
– In general, flat surface rendering provides an
accurate display
• Polygon is one polyhedron’s face (flat face)
• All light sources are sufficiently far, N．L = constant
• The viewing position is also sufficiently far, V．R =
constant
glShadeModel(GL_FLAT)
ksIl ( V  R )ns , if V  R  0 and N  L  0
Il ,spec 
 0.0, if V  R  0 or N  L  0
62

63. N
Gouraud surface
rendering
• Gouraud surface rendering is also called
intensity-interpolation surface rendering
– Linear interpolates vertex intensity
– Each polygon section of a tessellated curved
surface
• Determine the average unit normal vector at each
vertex of the polygon
• Apply an illumination model to obtain the light
intensity at that position
• Linearly interpolate the vertex intensities over the
projected area
glShadeModel(GL_SMOOTH)
N1  N2  N3  N4
N
N1  N2  N3  N4 63

64. Two surface rendering
Using Flat surface Using Gouraud
mesh rendering surface rendering
glEnable(GL_COLOR_MATERIAL); //object’s color
64

65. N’
Phong surface rendering
• Phong surface rendering is also called
normal-vector interpolation rendering
– Each polygon section of a tessellated curved
surface
• Determine the average unit normal vector at each
vertex
• Linearly interpolate the vertex normal over the
projected area
• Apply an illumination model at positions along scan
lines to calculate pixel intensities
N( )  (1  )N1  ( )N2
N '(  )  (1   )N3  (  )N2
65

66. OpenGL lights
• OpenGL light-source function
– light-source position
– Light-source colors
• OpenGL global lighting parameters
• OpenGL surface-property function
• OpenGL Spotlights
66

67. OpenGL light-source
function
• Multiple point light sources can be included
in OpenGL scene description which has
various properties.
glLight*(lightName, lightProperty, propertyValue);
– Function name’s suffix code: i (int) or f (float)
– v (vector):
• propertyValue use v to represent a pointer to an
array
• lightName: GL_LIGHT0,…,GL_LIGHT7
• lightProperty: can be assigned one of ten symbolic
property constants
67

68. OpenGL light-source
position
// light1 is designated as a local source at (2.0,0.0,3.0)
GLfloat light1PosType [ ] = {2.0, 0.0, 3.0, 1.0}
//light2 is a distant source with light emission in –y axis
GLfloat light2PosType [ ] = {0.0, 1.0, 0.0, 0.0}
glLightfv(GL_LIGHT1, GL_POSITION, light1PosType);
glEnable(GL_LIGHT1); // turn on light1
….
68

69. OpenGL Light-source
colors
• Light-source colors (R,G,B,A)
– The symbolic color-property
• GL_AMBIENT, GL_DIFFUSE and
GL_SPECULAR
GLfloat color1 [ ] = {0.0, 0.0, 0.0, 1.0}//black
GLfloat color2 [ ] = {1.0, 1.0, 1.0, 1.0}//white
glLightfv (GL_LIGHT3, GL_AMBIENT, color1);
…
69

70. Energylight = 1
dl
Energylight = 1/dl2
• Radial-intensity attenuation coefficients
with dl as the distance from a light-source
position
– Three OpenGL property constants
• GL_CONSTANT_ATTENUATION,
GL_LINEAR_ATTENUATION and
GL_QUADRATIC_ATTENUATION
• Each coefficients a0, a1, a2 <- which can be designated
a0
glLightfv (GL_LIGHT6, GL_CONSTANT_ATTENUATION, 1.5);
…
70

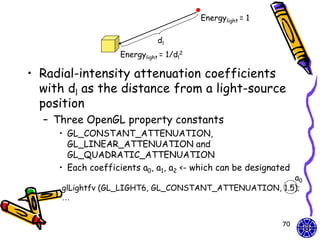
71. OpenGL global lighting
parameters
• OpenGL lighting parameters can be
specified at the global level
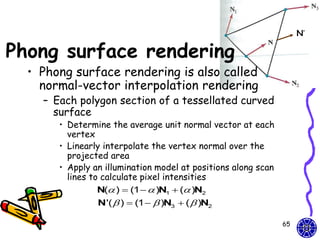
glLightModel* (paramName, ParamValue);
– Besides the ambient color for individual light
sources, we can also set it to be background
lighting as a global value
• Ex: set background lighting to a low-intensity dark-
blue color and an alpha value = 1.0
globalAmbient [ ] = {0.0, 0.0, 0.3, 1.0}
glLightModelfv(GL_LIGHT_MODEL_AMBIENT, globalAmbient);
Default global Ambient color = (0.2,0.2,0.2,1.0)
//dark gray
71

72. OpenGL surface-
property function
• Reflection coefficients and other optical properties
for surfaces
glMaterial*(surFace, surfProperty, propertyValue);
– Parameter surFace
• GL_FRONT, GL_BACK or GL_FRONT_AND_BACK
– Parameter surfProperty is a symbolic constant identifying a
surface parameter
• Isurf, ka, ks, or ns
– Parameter propertyValue is set to the corresponding value
with surfProperty
• All properties are specified as vector values
• Beside ns(the specular-reflection exponent)
72

73. Ambient & diffuse realization
• The ambient and diffuse coefficients
should be assigned the same vector values
– GL_AMBIENT_AND_DIFFUSE
• To set the specular-reflection exponent
– GL_SHININESS
• The range of the value : 0 ~ 128
diffuseCoeff [ ] = {0.2, 0.4, 0.9, 1.0};//light-blue color
specularCoeff [ ] = {1.0, 1.0, 1.0, 1.0};//white light
glMaterialfv (GL_FRONT_AND_BACK,
GL_AMBIENT_AND_DIFFUSE, diffuseCoeff);
glMaterialfv(GL_FRONT_AND_BACK, GL_SPECULAR, specularCoeff);
glMaterialfv(GL_FRONT_AND_BACK, GL_SHININESS, 25.0);
73

74. OpenGL Spotlights
• Spotlights is directional light sources
– Three OpenGL property constants for
directional effects
• GL_SPOT_DIRECTION, GL_SPOT_CUTOFF
and GL_SPOT_EXPONENT
– Ex: θl = 30°, cone axis= x-axis and the attenuation
exponent = 2.5
GLfloat dirVector [ ] = {1.0, 0.0, 0.0}; To object Vobj
glLightfv(GL_LIGHT4, GL_SPOT_DIRECTION, dirVector); vertex
α
glLightf(GL_LIGHT4, GL_SPOT_CUTOFF, 30.0);
glLightf(GL_LIGHT4, GL_SPOT_EXPONENT, 2.5);
cone axis
Light
source θl
74
demo