Download to read offline
![32
Fura 2-loaded cells showing the elevation of [Ca2+]
i
initiated at rear-end (anode side) and propagating through
entire cell body as a wave (small arrows).(E= 14 V/cm)
63
Promotion of fracture healing
• Electrical current triggers bone growth
• Piezoelectric effect within the collagen matrix
• Alternating current
– Applied transcutaneously
– Similar to diathermy units (no heat production)
• Direct current
– Implanted electrodes
64](https://image.slidesharecdn.com/lec3-200916091806/75/Fields-Lec-3-32-2048.jpg)
Uploaded bycairo university
Fields Lec 3
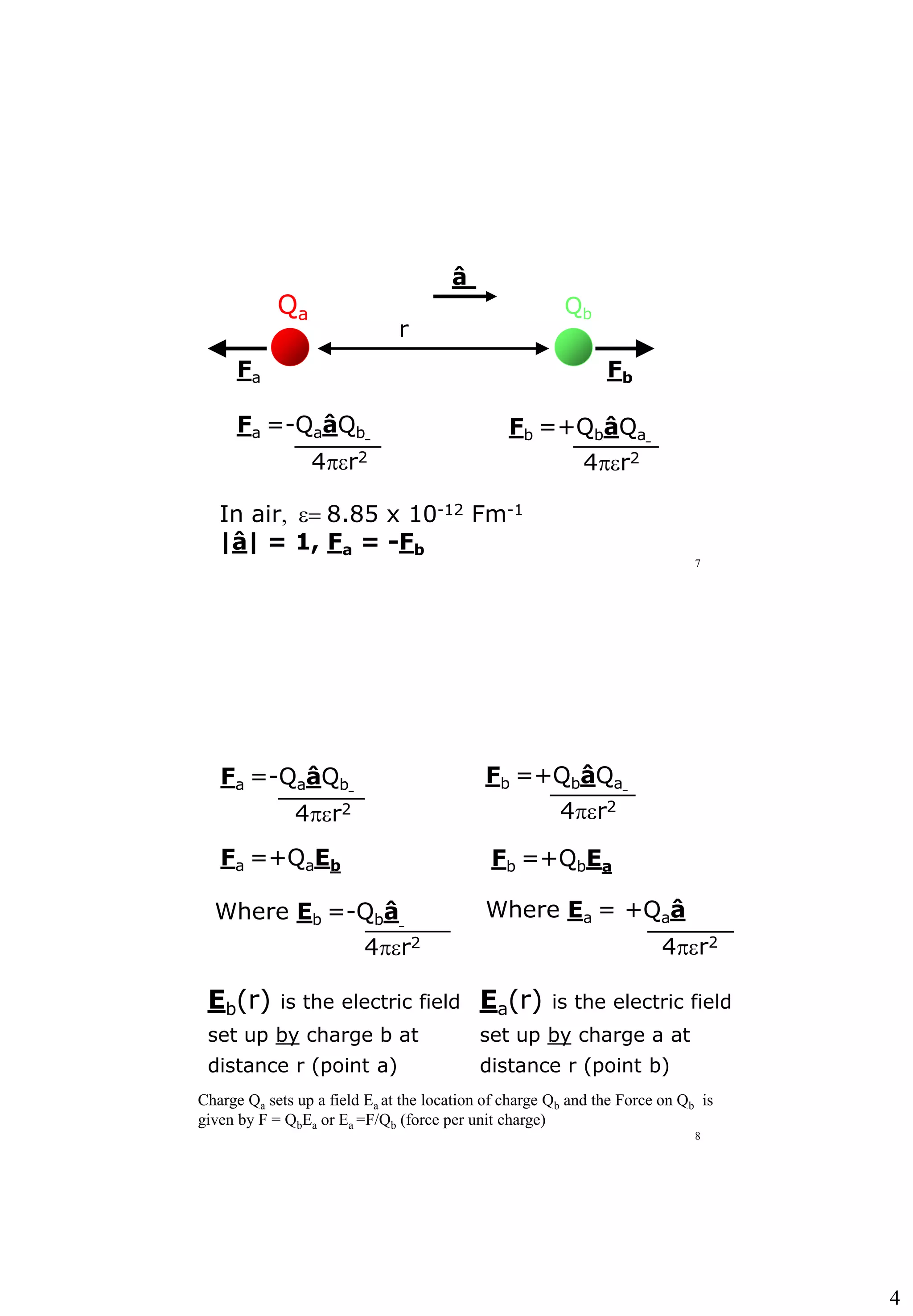
Here are some examples of FDA-approved therapeutic devices that use direct current (DC) electric fields: - Bone growth stimulators - Use pulsed electromagnetic fields or capacitively coupled electric fields to promote bone healing of fractures that are not healing on their own. - Transcutaneous electrical nerve stimulators (TENS) - Apply electric currents to stimulate nerves for pain relief and muscle rehabilitation. - Iontophoresis devices - Use low-level electrical currents to drive ionized drug molecules through the skin for local drug delivery. - Cardioversion/defibrillation devices - Apply controlled electric shocks to the heart to treat irregular heart rhythms like atrial fibrillation or ventricular fibrillation.
More Related Content
Fields Lec 3
- 1. 1 1 Electrostatic fields • Whystudy electrostatics? • Many applications in biology and medicine: -Diagnosis as incorporated in electrocardiograms, electroencephalograms and other recordings of organs with electrical activity) -Therapy as incorporated in diathermy, electro- poration, …… 2 • Electrostatics is the branch of science that deals with the phenomena arising from what seem to be stationary electric charges. • Two fundamental laws govern electrostatic fields: • 1. Coulomb’s law (Self Study) • 2. Gauss’s law (Check experiment on the net) • Both laws are based on experimental studies.
- 2.
- 3. 3 5 6 Coulomb’s Law • Theforce F between two point charges Q1 and Q2 is: 1. Along the line joining them 2. Directly proportional to the product of Q1 and Q2 3. Inversely proportional to the square of the distance R between them
- 4. 4 7 r FbFa Fa =-QaâQb 4per2 Fb =+QbâQa 4per2 â Inair, e= 8.85 x 10-12 Fm-1 |â| = 1, Fa = -Fb Qa Qb 8 Fa =-QaâQb 4per2 Fb =+QbâQa 4per2 Fa =+QaEb Fb =+QbEa Where Ea = +Qaâ 4per2 Where Eb =-Qbâ 4per2 Eb(r) is the electric field set up by charge b at distance r (point a) Ea(r) is the electric field set up by charge a at distance r (point b) Charge Qa sets up a field Ea at the location of charge Qb and the Force on Qb is given by F = QbEa or Ea =F/Qb (force per unit charge)
- 5. 5 9 10 Several Charges? • Ifthere are N charges Qa,Qb,….located at points with position vectors r1,r2,… the resultant force F on a charge Q located at point r is the vector sum of the forces exerted on Q by each of the charges Q1,Q2,….. +Qa +Qc +Qd -Qe -Qb Ea Eb Ec Ed Ee
- 6. 6 11 Many charges … •Q1, Q2, Q3 …QN • E = E1 + E2 + E3 … EN • E = SNEN = SN • OK for a handful of charges 2 04 ˆ r Qa E N N pe = 2 04 ˆ r Qa N pe 12 Many charges … -For a small numbers of charges: Q1(r1), Q2(r2) … QN(rN) is OK to describe a charge Q1 at position r1 etc. -For a large N: Instead use r(r) as the density (in Cm-3) of charge at a point r SNQN becomes ∫r(r)dxdydz = ∫∫∫volr(r)dv r = charge density
- 7.
- 8. 8 Equipotentials for apoint charge 15 16 Long straight line “rod” of charge of a uniform density rl r is the distance vector directed from the source to the field point dE R r dl x y E = (Ex, Ey)Ey Ex = L 2 r 0 r a 4 1 d E r pe x`
- 9. 9 17 • r =aRR - axx` • For every rl dx at +x there is a charge element rl dx at –x, which will produce a dE with components dER and -dEx Hence the axcomponents will cancel in the integration process. 2322 0 )(4 xR Rdx dER = pe r 2322 x 0 )( a 4 E xR xRdx d = Ra pe r 2322 0 )(4 xR dxx dEx = pe r == 2322 0 RR )(4 aaE xR dxR ER pe r R0 R 2 aE pe r = Spherical cells in an electric field (depolarization at the cathode and hyperpolarization at the anode) Vm = 3/2 ER cos
- 10. 10 Fibroblasts in aDC electric field (elongation perpendicular to the electric field vector 19 20 Electric Flux Density : • Flux : number of field lines that cross a normal area (measured in Coulombs per square meter) D = e0E = D.ds • One line of electric flux emanates from +1 C and terminates on – 1 C. • ε0 = 8.85 x 10-12 in a vacuum
- 11. 11 21 Gauss’s Law: Integralform = Qenc 22 Gauss’s Law - Integral form dvdsD dvQ dsDd Q v v v venc enc = = == = r r . .
- 12. 12 23 Gauss’s Law -Differential form =s v vdvsdD r vD r= =s v dvDsdD = v vv dvdvD r Divergence Theorem Remember: The divergence theorem states that the total outward flux of a vector field through the closed surface S is the same as the volume integral of the divergence of A. This equation says that the electric flux density D diverges from free charge rv 24 Gauss’s Law : Cartoon Version • The number of electric field lines leaving a closed surface is equal to the charge enclosed by that surface S(E-field-lines) a Charge Enclosed N Coulombs aN lines The surface is chosen such that D is normal or tangential to the Gaussian surface. When D is normal to the surface, D • dS = D dS. When D is tangential to the surface, D • dS = 0.
- 13. 13 25 Flux of rain(rainfall) through an area ds ds Rainfall Rainfall This area gets wetter! Flux rain = D.ds |D||ds| cos() Dds cos() Flux rain = 0 for 90° … cos() = 0 Flux rain = -Dds for 180° … cos() = -1 Generally, Flux rain = Dds cos() -1 < cos() < +1 26 rl Coulombs/m L Gauss’s law - Example Long straight “rod” of charge Construct a “Gaussian Surface” that reflects the symmetry of the charge - cylindrical in this case, then evaluate D.ds ds ds E, D ds E, D r
- 14. 14 27 ds E, D r Evaluate D.ds D.ds = D.ds curved surface + D.ds flat end faces • End faces, D & ds are perpendicular – D.ds on end faces = 0 – D.ds flat end faces = 0 • Flat end faces do not contribute! 28 Evaluate D.ds D.ds = D.ds curved surface only rl Coulombs/m L ds ds E, D D & ds parallel, D.ds = |D|´|ds| = Dds
- 15. 15 29 Evaluate D.ds D.ds curved surface only = Dds rl Coulombs/m L E, D D has the same strength D(r) everywhere on this surface. 30 Evaluate D.ds D.ds curved surface only = ds • = D ds = D area of curved surface • = D 2 p r L • So 2Dp r L = charge enclosed • Charge enclosed? • Charge/length length L = rl L rl Coulombs/m rL 2pr D
- 16. 16 31 Evaluate D.ds D.ds = charge enclosed 2pDr L = rl L • D(r) = rl 2pr • D(r) = rl âr 2pr 32 Discussion • |D| is proportional to 1/r – Gets weaker with distance • D points radially outwards (âr) • |D| is proportional to rl – More charge density = more field – Intuitively correct
- 17.
- 18.
- 19.
- 20. 20 39 HW: • Solve theprevious example using Gauss’s law in the differential form 40 Postulates of Electrostatics in Free Space Differential Form Integral Form - Static electric field is not solenoidal unless ρ = 0 - Static E-Fields are conservative or irrotational. If a vector field is curl-free, then it can be expressed as the gradient of a scalar field: -The total outward flux of the electric field intensity over any closed surface in free space equals to the total charge enclosed in the surface divided e0by (Gauss's Law) -The scalar line integral of the static electric field intensity around any closed path vanishes (KVL) 0 0 = = E E e r = = c s dlE Q dsE 0 0e VE =
- 21. 21 41 An oscillating electricfield (purple arcs) separates drug-delivery nanoparticles (yellow spheres) from blood (red spheres) and pulls them towards rings surrounding the chip's electrodes. The image is featured as the inside cover of the Oct. 14 issue of the journal Small. Credit: Stuart Ibsen and Steven Ibsen. 42
- 22.
- 23. 23 45 Material Classification • Materialsmay be classified in terms of their conductivity, in mhos per meter or Siemens per meter, as conductors and nonconductors, or technically as metals and insulators (or dielectrics). • A material with high conductivity ( >> 1) is referred to as a metal whereas one with low conductivity ( << 1) is referred to as an insulator. • A material whose conductivity lies somewhere between those of metals and insulators is called a semiconductor. • Based on the values of conductivity, materials such as copper and aluminum are metals, silicon and germanium are semiconductors, and glass and rubber are insulators. 46 • The conductivity of a material usually depends on temperature and frequency. • The conductivity of metals generally increases with decrease in temperature. • At temperatures near absolute zero (T = 0°K), some conductors exhibit infinite conductivity and are called superconductors. Lead and aluminum are typical examples of such metals. • Microscopically, the major difference between a metal and an insulator lies in the amount of electrons available for conduction of current. • Dielectric materials have few electrons available for conduction of current in contrast to metals, which have an abundance of free electrons.
- 24.
- 25. 25 49 Conductors in ElectricFields 50 Dielectrics in Electric Fields: Polarization
- 26. 26 51 Polarization vector 52 Conductors andDielectrics
- 27. 27 53 Conduction & DisplacementCurrents • Electric current is generally caused by the motion of electric charges. • The current (in amperes) through a given area is the electric charge passing through the area per unit time. • Current I = dQ / dt • If current I flows through a surface S, the current density Jn= I / S or I = Jn S assuming that the current density is perpendicular to the surface. If the current density is not normal to the surface, I = J • S • Thus, the total current flowing through a surface S is I = ∫ J . dS 54
- 28. 28 55 56 Electrical properties ofbody tissues • The human body is made of a large number of materials (tissues), each of them having specific properties. • Since biological tissues mainly consist of water, they behave neither as a conductor nor a dielectric, but as a lossy dielectric. • represents the ability of the material’s charge to be transported throughout its volume by an applied E-field. • e represents the ability of the material’s molecular dipoles to rotate or its charge to be stored by an applied external applied E- field. • The permittivity and conductivity of biological tissues are functions of frequency.
- 29.
- 30. 30 59 Grey Matter Effects ofE-Fields at Cellular Level • Excitation of nerve cells • Changes in cell membrane permeability • Protein synthesis • Stimulation of fibroblasts and osteoblasts • Modification of microcirculation 60
- 31. 31 Effects at TissueLevel • Skeletal muscle contraction • Smooth muscle contraction • Tissue regeneration 61 EF-induced migration in 3T3 mouse fibroblast cells 62
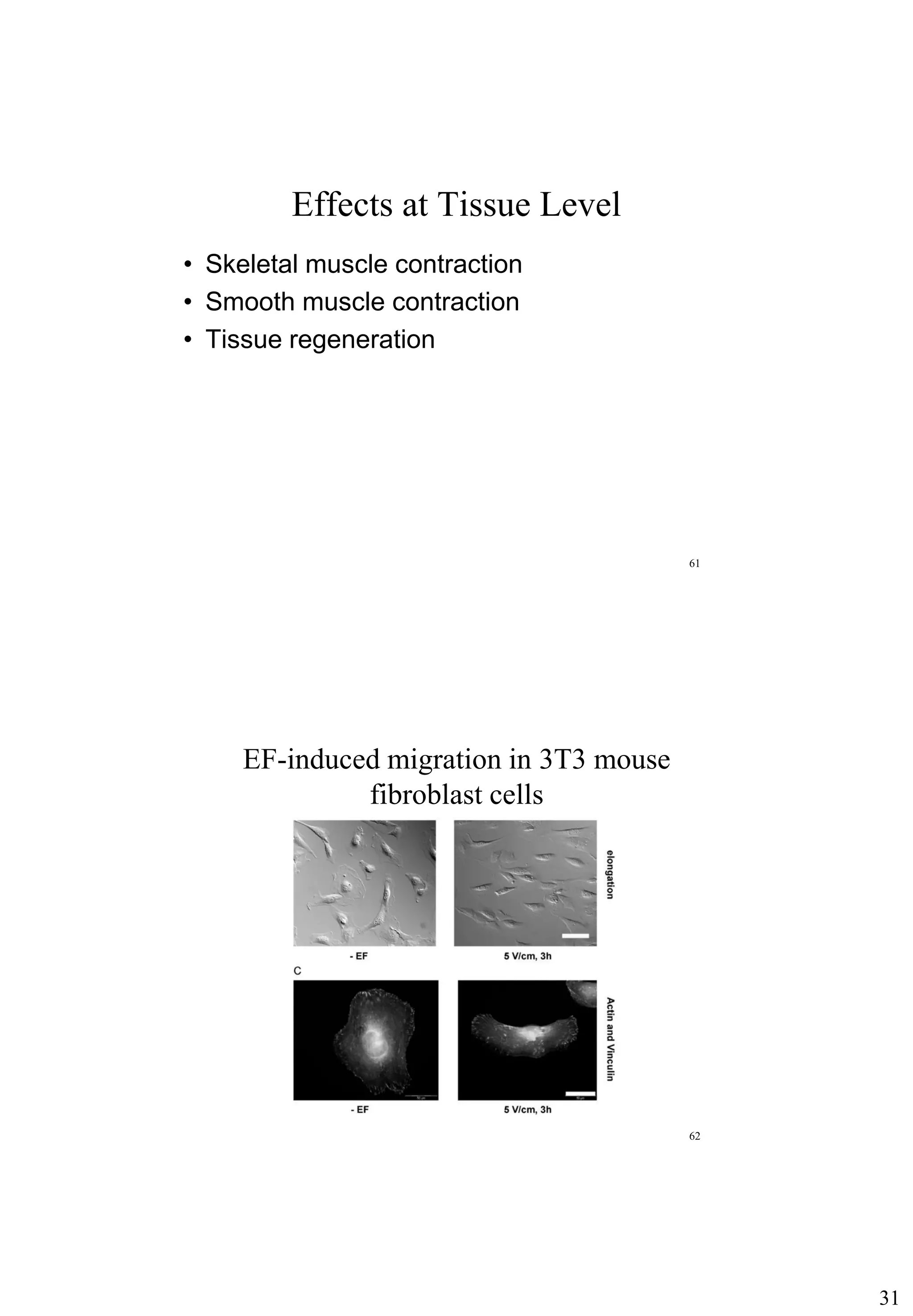
- 32. 32 Fura 2-loaded cellsshowing the elevation of [Ca2+] i initiated at rear-end (anode side) and propagating through entire cell body as a wave (small arrows).(E= 14 V/cm) 63 Promotion of fracture healing • Electrical current triggers bone growth • Piezoelectric effect within the collagen matrix • Alternating current – Applied transcutaneously – Similar to diathermy units (no heat production) • Direct current – Implanted electrodes 64
- 33. 33 HW • Present alist of FDA approved therapeutic devices that use DC electric fields. 65