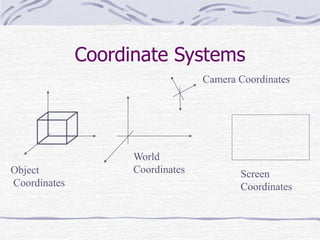
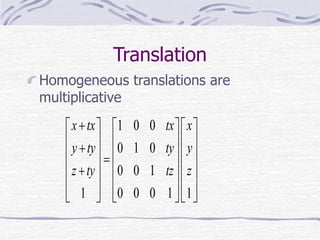
This document discusses computer graphics and the role of linear algebra in creating 2D images from 3D mathematical models. It explains that computer graphics uses transformations between different coordinate systems, such as object coordinates, world coordinates, camera coordinates, and screen coordinates, to render 3D scenes. These coordinate transformations involve affine transformations like rotation, translation, and scaling, which can be represented by homogeneous matrices. The document also describes how perspective projection is achieved through multiplication of points by a perspective matrix to give the illusion of depth.

1. Computer Graphics: A Case
Study in Linear Algebra
Deborah A. Trytten
Spring 2002

2. What is Graphics?
The collection of techniques used to
take mathematical models and create
images
Models are often 3D
Images are often 2D

3. What Math is Involved?
Extensive linear algebra
Change of coordinate systems
Affine transformations
Homogeneous matrices
Geometry
Calculus
Discrete Mathematics
Mathematical Modeling

4. The Elements
Objects
Catalog of reusable models
Usually a represented as a polygonal mesh
The Scene
Camera
Computer Screen

5. Desirable Properties
Speed
A single frame can have more than a
million pixels
Logical control of elements
Speed
Visual realism
Speed

6. Goal
Want to create a single matrix that:
Starts with points in a 3D object
Arranges them in a scene
Positions a camera in the scene
Projects a region of interest to 2D
Maps projected region of interest to the
computer screen

7. Coordinate Systems
Object
Coordinates
World
Coordinates
Camera Coordinates
Screen
Coordinates

8. Coordinate System Transforms
Start with points in object coordinates
Transform to world coordinates
Transform to camera coordinates
Project to 2D
Transform projected region of interest
to screen coordinates

9. Coordinate Transformations
Coordinate systems transformations
consist of three affine transformations
Rotation
Translation
Scaling
Shear is also affine
Used in one type of projection

10. Representation
We represent points in homogeneous
coordinates
(x, y, z) -> (x, y, z, 1)
(x, y, z, 1) = (xw, yw, zw, w)
Vectors
(x, y, z) -> (x, y, z, 0)
Distinguishing points and vectors is essential
in graphics
Adding vectors is OK
Adding points isn’t

11. Translation
Homogeneous translations are
multiplicative
x tx tx x
y ty ty y
z ty tz z
    1 0 0
  
     

0 1 0
      
    0 0 1
  
     
 1   0 0 0 1   1


12. Perspective Projection
Gives depth foreshortening

13. Mathematics of Perspective
P(x,y,z)
(x*,y*, N)
z=-N
z
x or y
x or y

14. Perspective Matrix
x* = xN/z
y* = yN/z
z* = N (z/z)
xN N 0 0 0
x
yN N y
zN N z
z
     
     
0 0 0
      
   0 0 0
  
     
   0 0 1 0   1


15. Result
P’ = (Object to World)P
P’’ = (World to Camera) P
P’’’ = Perspective P’’
Derived earlier
Result = (Projected to Screen) P’’’
Multiply all the matrices first
Each point is multiplied by only one
matrix!