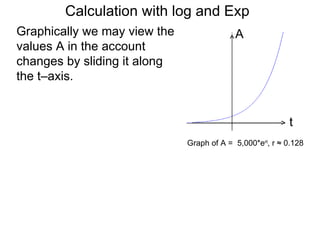
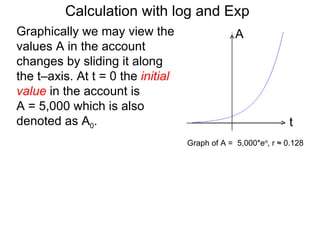
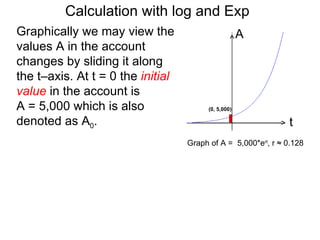
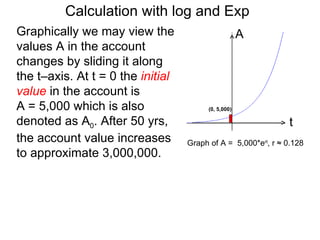
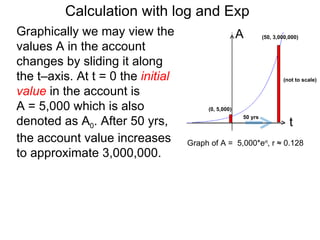
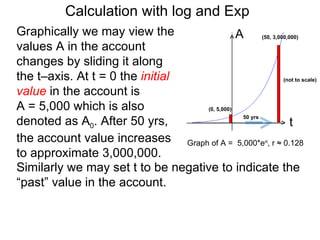
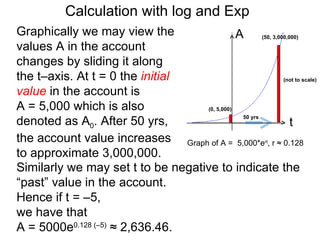
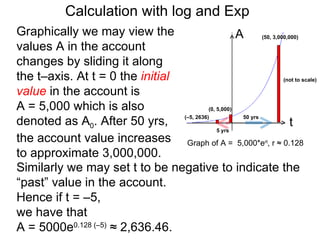
The document discusses solving numerical equations involving logarithmic and exponential functions in base 10 or base e. It provides examples of solving both log equations, by rewriting them in exponential form, and exponential equations, by rewriting them in logarithmic form. The key steps are to isolate the part containing the unknown, then rewrite the equation by "bringing down" exponents or taking the logarithm/exponential to solve for the unknown.

1. Calculation with log and Exp

2. Calculation with log and Exp
In this section, we solve simple numerical equations
involving log and exponential functions in base 10
or base e.

3. Calculation with log and Exp
In this section, we solve simple numerical equations
involving log and exponential functions in base 10
or base e. Most numerical calculations in science are
in these two bases.

4. Calculation with log and Exp
In this section, we solve simple numerical equations
involving log and exponential functions in base 10
or base e. Most numerical calculations in science are
in these two bases. We need a calculator that has
the following functions. ex, 10x, ln(x), and log(x).

5. Calculation with log and Exp
In this section, we solve simple numerical equations
involving log and exponential functions in base 10
or base e. Most numerical calculations in science are
in these two bases. We need a calculator that has
the following functions. ex, 10x, ln(x), and log(x).
All answers are given to 3 significant digits.

6. Calculation with log and Exp
In this section, we solve simple numerical equations
involving log and exponential functions in base 10
or base e. Most numerical calculations in science are
in these two bases. We need a calculator that has
the following functions. ex, 10x, ln(x), and log(x).
All answers are given to 3 significant digits.
Example A. Find the answers with a calculator.
6
a.10 3.32
b. √e = e1/6
c. log(4.35) d. ln(2/3)

7. Calculation with log and Exp
In this section, we solve simple numerical equations
involving log and exponential functions in base 10
or base e. Most numerical calculations in science are
in these two bases. We need a calculator that has
the following functions. ex, 10x, ln(x), and log(x).
All answers are given to 3 significant digits.
Example A. Find the answers with a calculator.
6
a.103.32
b. √e = e1/6
≈ 2090
c. log(4.35) d. ln(2/3)

8. Calculation with log and Exp
In this section, we solve simple numerical equations
involving log and exponential functions in base 10
or base e. Most numerical calculations in science are
in these two bases. We need a calculator that has
the following functions. ex, 10x, ln(x), and log(x).
All answers are given to 3 significant digits.
Example A. Find the answers with a calculator.
6
a.103.32
b. √e = e1/6
≈ 2090 ≈ 1.18
c. log(4.35) d. ln(2/3)

9. Calculation with log and Exp
In this section, we solve simple numerical equations
involving log and exponential functions in base 10
or base e. Most numerical calculations in science are
in these two bases. We need a calculator that has
the following functions. ex, 10x, ln(x), and log(x).
All answers are given to 3 significant digits.
Example A. Find the answers with a calculator.
6
a.103.32
b. √e = e1/6
≈ 2090 ≈ 1.18
c. log(4.35) d. ln(2/3)
≈0.638

10. Calculation with log and Exp
In this section, we solve simple numerical equations
involving log and exponential functions in base 10
or base e. Most numerical calculations in science are
in these two bases. We need a calculator that has
the following functions. ex, 10x, ln(x), and log(x).
All answers are given to 3 significant digits.
Example A. Find the answers with a calculator.
6
a.103.32
b. √e = e1/6
≈ 2090 ≈ 1.18
c. log(4.35) d. ln(2/3)
≈0.638 ≈ -0.405

11. Calculation with log and Exp
In this section, we solve simple numerical equations
involving log and exponential functions in base 10
or base e. Most numerical calculations in science are
in these two bases. We need a calculator that has
the following functions. ex, 10x, ln(x), and log(x).
All answers are given to 3 significant digits.
Example A. Find the answers with a calculator.
6
a.103.32
b. √e = e1/6
≈ 2090 ≈ 1.18
c. log(4.35) d. ln(2/3)
≈0.638 ≈ -0.405
These problems may be stated in alternate forms.

12. Calculation with log and Exp
Example B. Find the x
a. log(x) = 3.32 b. 1/6 = ln(x)
c. 10x = 4.35 d. 2/3 = ex

13. Calculation with log and Exp
Example B. Find the x
a. log(x) = 3.32 b. 1/6 = ln(x)
x =103.32 (≈ 2090)
c. 10x = 4.35 d. 2/3 = ex

14. Calculation with log and Exp
Example B. Find the x
a. log(x) = 3.32 b. 1/6 = ln(x)
x =103.32 (≈ 2090) e1/6 = x (≈ 1.18)
c. 10x = 4.35 d. 2/3 = ex

15. Calculation with log and Exp
Example B. Find the x
a. log(x) = 3.32 b. 1/6 = ln(x)
x =103.32 (≈ 2090) e1/6 = x (≈ 1.18)
c. 10x = 4.35 d. 2/3 = ex
x = log(4.35) (≈ 0.638)

16. Calculation with log and Exp
Example B. Find the x
a. log(x) = 3.32 b. 1/6 = ln(x)
x =103.32 (≈ 2090) e1/6 = x (≈ 1.18)
c. 10x = 4.35 d. 2/3 = ex
x = log(4.35) (≈ 0.638) ln(2/3) = x (≈ -0.405)

17. Calculation with log and Exp
Example B. Find the x
a. log(x) = 3.32 b. 1/6 = ln(x)
x =103.32 (≈ 2090) e1/6 = x (≈ 1.18)
c. 10x = 4.35 d. 2/3 = ex
x = log(4.35) (≈ 0.638) ln(2/3) = x (≈ -0.405)
An equation is called a log-equation if the unknown is
in the log-function as in parts a and b above.

18. Calculation with log and Exp
Example B. Find the x
a. log(x) = 3.32 b. 1/6 = ln(x)
x =103.32 (≈ 2090) e1/6 = x (≈ 1.18)
c. 10x = 4.35 d. 2/3 = ex
x = log(4.35) (≈ 0.638) ln(2/3) = x (≈ -0.405)
An equation is called a log-equation if the unknown is
in the log-function as in parts a and b above.
An equation is called an exponential equations if the
unknown is in the exponent as in parts c and d.

19. Calculation with log and Exp
Example B. Find the x
a. log(x) = 3.32 b. 1/6 = ln(x)
x =103.32 (≈ 2090) e1/6 = x (≈ 1.18)
c. 10x = 4.35 d. 2/3 = ex
x = log(4.35) (≈ 0.638) ln(2/3) = x (≈ -0.405)
An equation is called a log-equation if the unknown is
in the log-function as in parts a and b above.
An equation is called an exponential equations if the
unknown is in the exponent as in parts c and d.
To solve log-equations, drop the log and write the
problems in exp-form.

20. Calculation with log and Exp
Example B. Find the x
a. log(x) = 3.32 b. 1/6 = ln(x)
x =103.32 (≈ 2090) e1/6 = x (≈ 1.18)
c. 10x = 4.35 d. 2/3 = ex
x = log(4.35) (≈ 0.638) ln(2/3) = x (≈ -0.405)
An equation is called a log-equation if the unknown is
in the log-function as in parts a and b above.
An equation is called an exponential equations if the
unknown is in the exponent as in parts c and d.
To solve log-equations, drop the log and write the
problems in exp-form. To solve exponential
equations, lower the exponents and write the
problems in log-form.

21. Calculation with log and Exp
More precisely, to solve exponential equations,

22. Calculation with log and Exp
More precisely, to solve exponential equations:
I. isolate the exponential part that contains the x,

23. Calculation with log and Exp
More precisely, to solve exponential equations:
I. isolate the exponential part that contains the x,
II. bring down the exponents by writing it in log-form.

24. Calculation with log and Exp
More precisely, to solve exponential equations:
I. isolate the exponential part that contains the x,
II. bring down the exponents by writing it in log-form.
Example C. Solve 25 = 7*102x

25. Calculation with log and Exp
More precisely, to solve exponential equations:
I. isolate the exponential part that contains the x,
II. bring down the exponents by writing it in log-form.
Example C. Solve 25 = 7*102x
Isolate the exponential part containing the x,
25/7 = 102x

26. Calculation with log and Exp
More precisely, to solve exponential equations:
I. isolate the exponential part that contains the x,
II. bring down the exponents by writing it in log-form.
Example C. Solve 25 = 7*102x
Isolate the exponential part containing the x,
25/7 = 102x
Bring down the x by restating it in log-form.
log(25/7) = 2x

27. Calculation with log and Exp
More precisely, to solve exponential equations:
I. isolate the exponential part that contains the x,
II. bring down the exponents by writing it in log-form.
Example C. Solve 25 = 7*102x
Isolate the exponential part containing the x,
25/7 = 102x
Bring down the x by restating it in log-form.
log(25/7) = 2x
log(25/7) = x
2

28. Calculation with log and Exp
More precisely, to solve exponential equations:
I. isolate the exponential part that contains the x,
II. bring down the exponents by writing it in log-form.
Example C. Solve 25 = 7*102x
Isolate the exponential part containing the x,
25/7 = 102x
Bring down the x by restating it in log-form.
log(25/7) = 2x
log(25/7) = x ≈ 0.276
2

29. Calculation with log and Exp
More precisely, to solve exponential equations:
I. isolate the exponential part that contains the x,
II. bring down the exponents by writing it in log-form.
Example C. Solve 25 = 7*102x
Isolate the exponential part containing the x,
25/7 = 102x
Bring down the x by restating it in log-form.
log(25/7) = 2x
log(25/7) = x ≈ 0.276
2
Exact answer Approx. answer

30. Calculation with log and Exp
Example D. Solve 2.3*e2-3x + 4.1 = 12.5

31. Calculation with log and Exp
Example D. Solve 2.3*e2-3x + 4.1 = 12.5
Isolate the exp-part. 2.3*e2-3x + 4.1 = 12.5

32. Calculation with log and Exp
Example D. Solve 2.3*e2-3x + 4.1 = 12.5
Isolate the exp-part. 2.3*e2-3x + 4.1 = 12.5
2.3*e2-3x = 12.5 – 4.1
2.3*e2-3x = 8.4

33. Calculation with log and Exp
Example D. Solve 2.3*e2-3x + 4.1 = 12.5
Isolate the exp-part. 2.3*e2-3x + 4.1 = 12.5
2.3*e2-3x = 12.5 – 4.1
2.3*e2-3x = 8.4
e2-3x = 8.4/2.3

34. Calculation with log and Exp
Example D. Solve 2.3*e2-3x + 4.1 = 12.5
Isolate the exp-part. 2.3*e2-3x + 4.1 = 12.5
2.3*e2-3x = 12.5 – 4.1
2.3*e2-3x = 8.4
e2-3x = 8.4/2.3
Restate in log-form. 2 – 3x = ln(8.4/2.3)

35. Calculation with log and Exp
Example D. Solve 2.3*e2-3x + 4.1 = 12.5
Isolate the exp-part. 2.3*e2-3x + 4.1 = 12.5
2.3*e2-3x = 12.5 – 4.1
2.3*e2-3x = 8.4
e2-3x = 8.4/2.3
Restate in log-form. 2 – 3x = ln(8.4/2.3)
Solve for x. 2 – ln(8.4/2.3) = 3x

36. Calculation with log and Exp
Example D. Solve 2.3*e2-3x + 4.1 = 12.5
Isolate the exp-part. 2.3*e2-3x + 4.1 = 12.5
2.3*e2-3x = 12.5 – 4.1
2.3*e2-3x = 8.4
e2-3x = 8.4/2.3
Restate in log-form. 2 – 3x = ln(8.4/2.3)
Solve for x. 2 – ln(8.4/2.3) = 3x
2-ln(8.4/2.3) = x
3

37. Calculation with log and Exp
Example D. Solve 2.3*e2-3x + 4.1 = 12.5
Isolate the exp-part. 2.3*e2-3x + 4.1 = 12.5
2.3*e2-3x = 12.5 – 4.1
2.3*e2-3x = 8.4
e2-3x = 8.4/2.3
Restate in log-form. 2 – 3x = ln(8.4/2.3)
Solve for x. 2 – ln(8.4/2.3) = 3x
2-ln(8.4/2.3) = x ≈ 0.235
3

38. Calculation with log and Exp
Example D. Solve 2.3*e2-3x + 4.1 = 12.5
Isolate the exp-part. 2.3*e2-3x + 4.1 = 12.5
2.3*e2-3x = 12.5 – 4.1
2.3*e2-3x = 8.4
e2-3x = 8.4/2.3
Restate in log-form. 2 – 3x = ln(8.4/2.3)
Solve for x. 2 – ln(8.4/2.3) = 3x
2-ln(8.4/2.3) = x ≈ 0.235
3
We solve a log-equation in analogous fashion.

39. Calculation with log and Exp
Example D. Solve 2.3*e2-3x + 4.1 = 12.5
Isolate the exp-part. 2.3*e2-3x + 4.1 = 12.5
2.3*e2-3x = 12.5 – 4.1
2.3*e2-3x = 8.4
e2-3x = 8.4/2.3
Restate in log-form. 2 – 3x = ln(8.4/2.3)
Solve for x. 2 – ln(8.4/2.3) = 3x
2-ln(8.4/2.3) = x ≈ 0.235
3
We solve a log-equation in analogous fashion.
I. isolate the log part that contains the x,
II. drop the log by writing it in exp-form.

40. Calculation with log and Exp
Example E. Solve 9*log(2x+1)= 7

41. Calculation with log and Exp
Example E. Solve 9*log(2x+1)= 7
Isolate the log-part, log(2x+1) = 7/9

42. Calculation with log and Exp
Example E. Solve 9*log(2x+1)= 7
Isolate the log-part, log(2x+1) = 7/9
Write it in exp-form 2x + 1 = 107/9

43. Calculation with log and Exp
Example E. Solve 9*log(2x+1)= 7
Isolate the log-part, log(2x+1) = 7/9
Write it in exp-form 2x + 1 = 107/9
Save for x.

44. Calculation with log and Exp
Example E. Solve 9*log(2x+1)= 7
Isolate the log-part, log(2x+1) = 7/9
Write it in exp-form 2x + 1 = 107/9
Save for x. 2x = 107/9 – 1
x = (107/9 – 1)/2

45. Calculation with log and Exp
Example E. Solve 9*log(2x+1)= 7
Isolate the log-part, log(2x+1) = 7/9
Write it in exp-form 2x + 1 = 107/9
Save for x. 2x = 107/9 – 1
x = (107/9 – 1)/2 ≈ 2.50

46. Calculation with log and Exp
Example E. Solve 9*log(2x+1)= 7
Isolate the log-part, log(2x+1) = 7/9
Write it in exp-form 2x + 1 = 107/9
Save for x. 2x = 107/9 – 1
x = (107/9 – 1)/2 ≈ 2.50
Example F. Solve 2.3*log(2–3x)+4.1 = 12.5

47. Calculation with log and Exp
Example E. Solve 9*log(2x+1)= 7
Isolate the log-part, log(2x+1) = 7/9
Write it in exp-form 2x + 1 = 107/9
Save for x. 2x = 107/9 – 1
x = (107/9 – 1)/2 ≈ 2.50
Example F. Solve 2.3*log(2–3x)+4.1 = 12.5
2.3*log(2–3x) + 4.1 = 12.5

48. Calculation with log and Exp
Example E. Solve 9*log(2x+1)= 7
Isolate the log-part, log(2x+1) = 7/9
Write it in exp-form 2x + 1 = 107/9
Save for x. 2x = 107/9 – 1
x = (107/9 – 1)/2 ≈ 2.50
Example F. Solve 2.3*log(2–3x)+4.1 = 12.5
2.3*log(2–3x) + 4.1 = 12.5
2.3*log(2–3x) = 12.5 – 4.1
2.3*log(2–3x) = 8.4

49. Calculation with log and Exp
Example E. Solve 9*log(2x+1)= 7
Isolate the log-part, log(2x+1) = 7/9
Write it in exp-form 2x + 1 = 107/9
Save for x. 2x = 107/9 – 1
x = (107/9 – 1)/2 ≈ 2.50
Example F. Solve 2.3*log(2–3x)+4.1 = 12.5
2.3*log(2–3x) + 4.1 = 12.5
2.3*log(2–3x) = 12.5 – 4.1
2.3*log(2–3x) = 8.4
log(2 – 3x) = 8.4/2.3

50. Calculation with log and Exp
Example E. Solve 9*log(2x+1)= 7
Isolate the log-part, log(2x+1) = 7/9
Write it in exp-form 2x + 1 = 107/9
Save for x. 2x = 107/9 – 1
x = (107/9 – 1)/2 ≈ 2.50
Example F. Solve 2.3*log(2–3x)+4.1 = 12.5
2.3*log(2–3x) + 4.1 = 12.5
2.3*log(2–3x) = 12.5 – 4.1
2.3*log(2–3x) = 8.4
log(2 – 3x) = 8.4/2.3
2 – 3x = 108.4/2.3

51. Calculation with log and Exp
Example E. Solve 9*log(2x+1)= 7
Isolate the log-part, log(2x+1) = 7/9
Write it in exp-form 2x + 1 = 107/9
Save for x. 2x = 107/9 – 1
x = (107/9 – 1)/2 ≈ 2.50
Example F. Solve 2.3*log(2–3x)+4.1 = 12.5
2.3*log(2–3x) + 4.1 = 12.5
2.3*log(2–3x) = 12.5 – 4.1
2.3*log(2–3x) = 8.4
log(2 – 3x) = 8.4/2.3
2 – 3x = 108.4/2.3
2 – 108.4/2.3 = 3x

52. Calculation with log and Exp
Example E. Solve 9*log(2x+1)= 7
Isolate the log-part, log(2x+1) = 7/9
Write it in exp-form 2x + 1 = 107/9
Save for x. 2x = 107/9 – 1
x = (107/9 – 1)/2 ≈ 2.50
Example F. Solve 2.3*log(2–3x)+4.1 = 12.5
2.3*log(2–3x) + 4.1 = 12.5
2.3*log(2–3x) = 12.5 – 4.1
2.3*log(2–3x) = 8.4
log(2 – 3x) = 8.4/2.3
2 – 3x = 108.4/2.3
2 – 108.4/2.3 = 3x
2 – 108.4/2.3 = x ≈ -1495
3

53. Calculation with log and Exp
Example G.
a. We deposited $5,000 in an account that
compounds continuously. After 10 years the total
value is $18,000. Find the interest rate r.

54. Calculation with log and Exp
Example G.
a. We deposited $5,000 in an account that
compounds continuously. After 10 years the total
value is $18,000. Find the interest rate r.
We use the Compound Interest Formula
Pert = A with the values
P = 5,000, A= 18,000 and that t = 10

55. Calculation with log and Exp
Example G.
a. We deposited $5,000 in an account that
compounds continuously. After 10 years the total
value is $18,000. Find the interest rate r.
We use the Compound Interest Formula
Pert = A with the values
P = 5,000, A= 18,000 and that t = 10 so
5,000e 10r = 18,000

56. Calculation with log and Exp
Example G.
a. We deposited $5,000 in an account that
compounds continuously. After 10 years the total
value is $18,000. Find the interest rate r.
We use the Compound Interest Formula
Pert = A with the values
P = 5,000, A= 18,000 and that t = 10 so
5,000e 10r = 18,000
Hence
e10r = 18,000/5,000 = 3.6

57. Calculation with log and Exp
Example G.
a. We deposited $5,000 in an account that
compounds continuously. After 10 years the total
value is $18,000. Find the interest rate r.
We use the Compound Interest Formula
Pert = A with the values
P = 5,000, A= 18,000 and that t = 10 so
5,000e 10r = 18,000
Hence
e10r = 18,000/5,000 = 3.6
Apply the natural log to both sides, we have that
10r = In (3.6)

58. Calculation with log and Exp
Example G.
a. We deposited $5,000 in an account that
compounds continuously. After 10 years the total
value is $18,000. Find the interest rate r.
We use the Compound Interest Formula
Pert = A with the values
P = 5,000, A= 18,000 and that t = 10 so
5,000e 10r = 18,000
Hence
e10r = 18,000/5,000 = 3.6
Apply the natural log to both sides, we have that
10r = In (3.6) or r = In (3.6) /10 ≈ 12.8 %.

59. Calculation with log and Exp
b. Write down the specific compound interest
formula in the variable t. How much will there be in
the account if we leave the account for 50 years?

60. Calculation with log and Exp
b. Write down the specific compound interest
formula in the variable t. How much will there be in
the account if we leave the account for 50 years?
We have that P = 5,000, A= 18,000 and r = 0.128.

61. Calculation with log and Exp
b. Write down the specific compound interest
formula in the variable t. How much will there be in
the account if we leave the account for 50 years?
We have that P = 5,000, A= 18,000 and r = 0.128.
Put these value in the Compound Interest Formula
A = Pert

62. Calculation with log and Exp
b. Write down the specific compound interest
formula in the variable t. How much will there be in
the account if we leave the account for 50 years?
We have that P = 5,000, A= 18,000 and r = 0.128.
Put these value in the Compound Interest Formula
A = Pert we get the specific formula
A = 5,000*e0.0128t

63. Calculation with log and Exp
b. Write down the specific compound interest
formula in the variable t. How much will there be in
the account if we leave the account for 50 years?
We have that P = 5,000, A= 18,000 and r = 0.128.
Put these value in the Compound Interest Formula
A = Pert we get the specific formula
A = 5,000*e0.0128t
In 50 years, t = 50,

64. Calculation with log and Exp
b. Write down the specific compound interest
formula in the variable t. How much will there be in
the account if we leave the account for 50 years?
We have that P = 5,000, A= 18,000 and r = 0.128.
Put these value in the Compound Interest Formula
A = Pert we get the specific formula
A = 5,000*e0.0128t
In 50 years, t = 50,
we have that
A = 5,000*e0.128 (50)

65. Calculation with log and Exp
b. Write down the specific compound interest
formula in the variable t. How much will there be in
the account if we leave the account for 50 years?
We have that P = 5,000, A= 18,000 and r = 0.128.
Put these value in the Compound Interest Formula
A = Pert we get the specific formula
A = 5,000*e0.0128t
In 50 years, t = 50,
we have that
A = 5,000*e0.128 (50)
≈ 5,000*e6.4
≈ $3,009,225.19

66. Calculation with log and Exp
Graphically we may view the
values A in the account
changes by sliding it along
the t–axis.

67. Calculation with log and Exp
Graphically we may view the A
values A in the account
changes by sliding it along
the t–axis.
t
Graph of A = 5,000*ert, r ≈ 0.128

68. Calculation with log and Exp
Graphically we may view the A
values A in the account
changes by sliding it along
the t–axis. At t = 0 the initial
value in the account is
A = 5,000 which is also
denoted as A0. t
Graph of A = 5,000*ert, r ≈ 0.128

69. Calculation with log and Exp
Graphically we may view the A
values A in the account
changes by sliding it along
the t–axis. At t = 0 the initial
value in the account is
A = 5,000 which is also (0, 5,000)
denoted as A0. t
Graph of A = 5,000*ert, r ≈ 0.128

70. Calculation with log and Exp
Graphically we may view the A
values A in the account
changes by sliding it along
the t–axis. At t = 0 the initial
value in the account is
A = 5,000 which is also (0, 5,000)
denoted as A0. After 50 yrs, t
the account value increases Graph of A = 5,000*ert, r ≈ 0.128
to approximate 3,000,000.

71. Calculation with log and Exp
Graphically we may view the A (50, 3,000,000)
values A in the account
changes by sliding it along
the t–axis. At t = 0 the initial (not to scale)
value in the account is
A = 5,000 which is also (0, 5,000)
denoted as A0. After 50 yrs, 50 yrs
t
the account value increases Graph of A = 5,000*ert, r ≈ 0.128
to approximate 3,000,000.

72. Calculation with log and Exp
Graphically we may view the A (50, 3,000,000)
values A in the account
changes by sliding it along
the t–axis. At t = 0 the initial (not to scale)
value in the account is
A = 5,000 which is also (0, 5,000)
denoted as A0. After 50 yrs, 50 yrs
t
the account value increases Graph of A = 5,000*e , r ≈ 0.128
rt
to approximate 3,000,000.
Similarly we may set t to be negative to indicate the
“past” value in the account.

73. Calculation with log and Exp
Graphically we may view the A (50, 3,000,000)
values A in the account
changes by sliding it along
the t–axis. At t = 0 the initial (not to scale)
value in the account is
A = 5,000 which is also (0, 5,000)
denoted as A0. After 50 yrs, 50 yrs
t
the account value increases Graph of A = 5,000*e , r ≈ 0.128
rt
to approximate 3,000,000.
Similarly we may set t to be negative to indicate the
“past” value in the account.
Hence if t = –5,
we have that
A = 5000e0.128 (–5) ≈ 2,636.46.

74. Calculation with log and Exp
Graphically we may view the A (50, 3,000,000)
values A in the account
changes by sliding it along
the t–axis. At t = 0 the initial (not to scale)
value in the account is
A = 5,000 which is also (0, 5,000)
denoted as A0. After 50 yrs, (–5, 2636) 50 yrs
t
5 yrs
the account value increases Graph of A = 5,000*e , r ≈ 0.128 rt
to approximate 3,000,000.
Similarly we may set t to be negative to indicate the
“past” value in the account.
Hence if t = –5,
we have that
A = 5000e0.128 (–5) ≈ 2,636.46.

75. Calculation with log and Exp
Exercise A.Solve the following exponential equations, give
the exact and the approximate solutions.
1. 5e2x = 7 2. 3e - 2x+1 = 6
3. 4 – e 3x+ 1 = 2 4. 2* 10 3x - 2 = 5
5. 6 + 3* 10 1- x = 10 6. -7 – 3*10 2x - 1 = -24
7. 8 = 12 – 2e 2- x 8. 5*10 2 - 3x + 3 = 14
Exercise B. Solve the following log equations, give the exact
and the approximate solutions.
9. log(3x+1) = 3/5 10. ln(2 – x) = -2/3
11. 2log(2x –3) = 1/3 12. 2 + log(4 – 2x) = -8
13. 3 – 5ln(3x +1) = -8 14. -3 +5log(1 – 2x) = 9
15. 2ln(2x – 1) – 3 = 5 16. 7 – 2ln(12x+15) =23
Exercise C.
17. How many years will it take for $1 compounded
continuously at the rate r = 4% to double to $2?
How about at r = 8%? at r = 12%? at r = 16%?

76. Calculation with log and Exp
18. In problem 17 would the “doubling times” be different if
the initial deposit is $1,000, i.e. for the $1,000 to grow to
$2,000? Justify your answer.
19. In fact the doubling time is t = ln(2)/r which does not
depend on the amount of the initial deposit P. A useful
approximation for the calculations is to use In(2) ≈ 0.72 so that
t ≈ 0.72 / r. This is called the 72–rule for the doubling times.
20. We deposited $1,000 in a account compounded
continuously at the rate r. After 20 years the account grew to
$20,000. Find r.
21. Continue with problem 20, write down the specific
compound interest formula. How much will there be in the
account if we leave the account for 30 years?
22. Continue with problem 20, how much time will it take for
the account to grow to $ I million?

77. Calculation with log and Exp
23. We deposited $5,000 in a account compounded
continuously at the rate r. After 15 years the account grew to
$12,000. Find r.
24. Continue with problem 23, write down the specific
compound interest formula. How much will there be in the
account if we leave the account for 100 years?
25. Continue with problem 23, how much time will it take for
the account to grow to $ I million?
26. We deposited $P in an account compounded continuously
at r = 5½%. After 5 years there is $5,000 in the account. Find
P. Continue with problem 26, write down the specific
27.
compound interest formula. How much will there be in the
account if we leave the account for 100 years?
28. Continue with problem 26, how much time will it take for
the account to grow to $ I million?

78. Calculation with log and Exp
Solve the following exponential equations, give the exact
and the approximate solutions.
1. 5e2x = 7 2. 3e - 2x+1 = 6
Exact. x = ½* ln(7/5) Exact. x = (1 – ln(2)) /2
Aproxímate. 0.168 Aproxímate. 0.153
3. 4 – e 3x+ 1 = 2 4. 2* 10 3x - 2 = 5
Exact. x = (ln(2) – 1)/3 Exact. x = (log(5/2) + 2)/3
Approximate. - 0.102 Approximate. 0.799
5. 6 + 3* 10 1- x = 10 6. -7 – 3*10 2x - 1 = -24
Exact. x = 1 – log(4/3) Exact. x = (log(17/3)+1)/2
Aproxímate. 0.875 Aproxímate. 0.877

79. Solve the following log equations, give the exact and the
approximate solutions.
9. log(3x+1) = 3/5 10. ln(2 – x) = -2/3
Exact. x = (103/5 – 1)/3 Exact. x = 2 – e -2/3
Approximate. 0.994 Approximate. 1.49
11. 2log(2x –3) = 1/3 12. 2 + log(4 – 2x) = -8
Exact. x = (101/6 + 3)/2 Exact. x = (4 – 10-10)/2
Approximate. 2.23 Approximate. 2.000
13. 3 – 5ln(3x +1) = -8 14. -3 +5log(1 – 2x) = 9
Exact. x = (e11/5 – 1 )/3 Exact. x = (1 – 10 12/5)/2
Approximate. 2.68 Approximate. -125
15. 2ln(2x – 1) – 3 = 5 16. 7 – 2ln(12x+15) =23