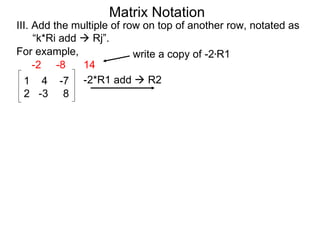
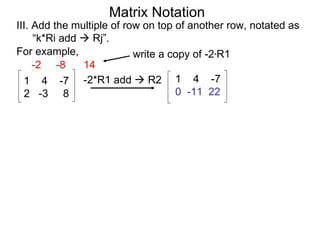
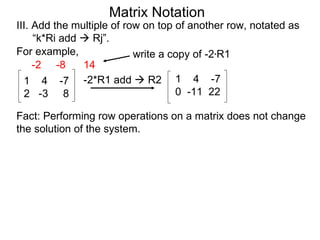
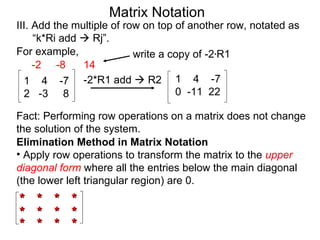
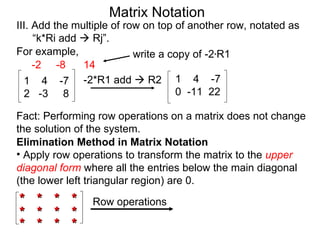
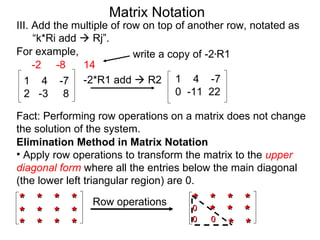
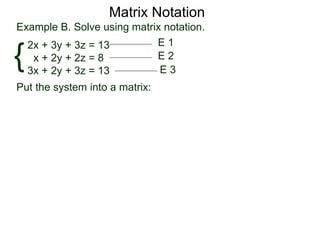
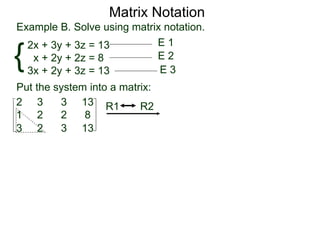
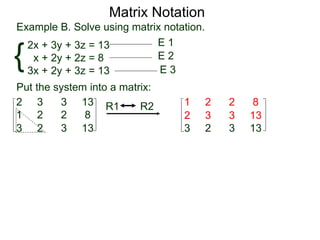
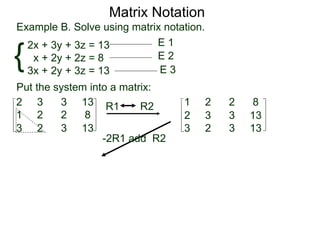
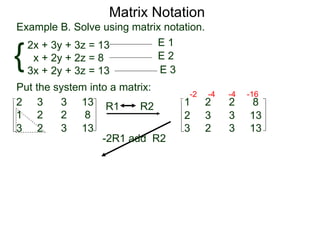
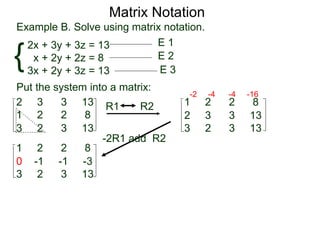
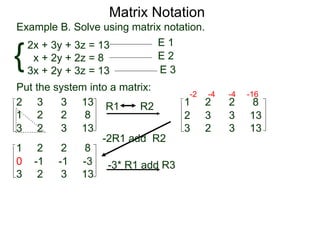
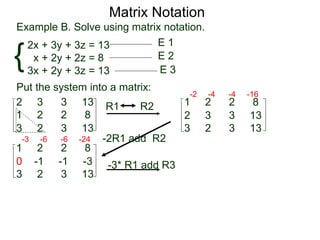
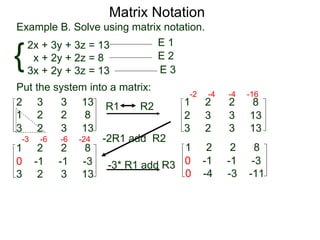
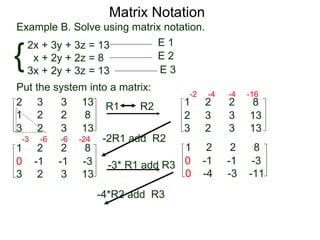
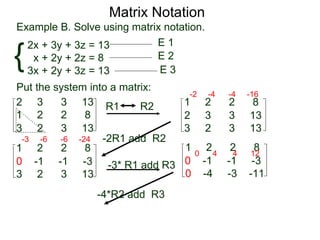
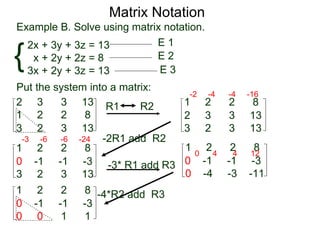
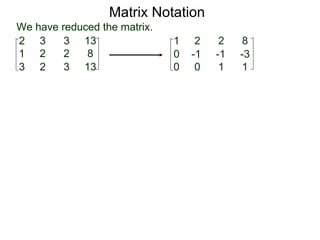
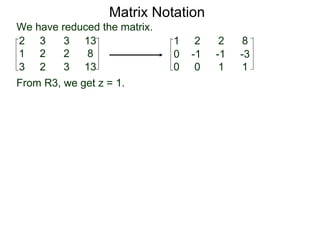
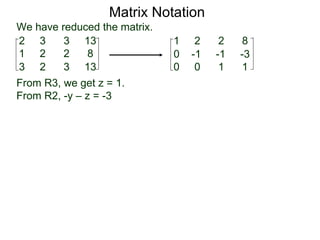
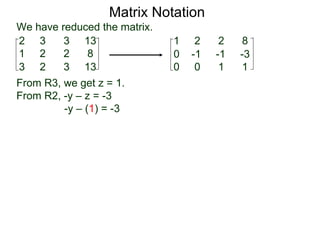
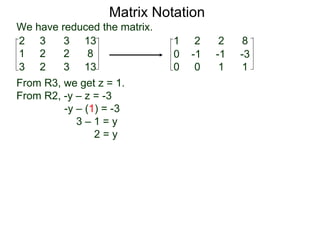
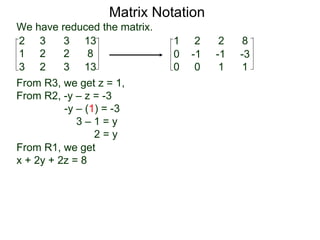
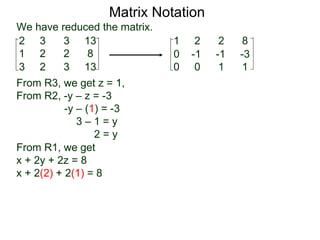
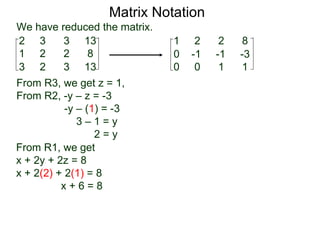
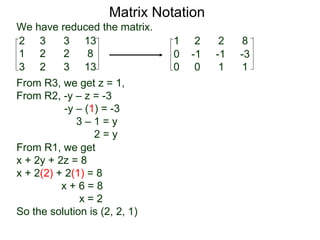
The document discusses matrix notation for representing and solving systems of linear equations. A matrix is defined as a rectangular table of numbers, and systems of linear equations can be represented as matrices with rows corresponding to equations and columns to variables. Three row operations - row switching, row scaling, and adding row multiples - can be performed on matrices while preserving the solution(s) to the corresponding system of equations. The elimination method uses row operations to transform a matrix representing a system into upper triangular form to solve for the variables.

1. Matrix Notation

2. Matrix Notation
A matrix is a rectangular table of numbers.

3. Matrix Notation
A matrix is a rectangular table of numbers.
For example
-1 2 -1
5 2 -3 6 -2 3
4 -1 0 11 9 -4
are matrices.

4. Matrix Notation
A matrix is a rectangular table of numbers.
For example
-1 2 -1
5 2 -3 6 -2 3
4 -1 0 11 9 -4
are matrices. Systems of linear equations can be put into
matrices then solved using matrix notation and elimination
method.

5. Matrix Notation
A matrix is a rectangular table of numbers.
For example
-1 2 -1
5 2 -3 6 -2 3
4 -1 0 11 9 -4
are matrices. Systems of linear equations can be put into
matrices then solved using matrix notation and elimination
method.
For example, if we put the following system into a matrix,
x + 4y = –7 Eq. 1
{2x – 3y = 8 Eq. 2

6. Matrix Notation
A matrix is a rectangular table of numbers.
For example
-1 2 -1
5 2 -3 6 -2 3
4 -1 0 11 9 -4
are matrices. Systems of linear equations can be put into
matrices then solved using matrix notation and elimination
method.
For example, if we put the following system into a matrix,
x + 4y = –7 Eq. 1
{2x – 3y = 8 Eq. 2
we get
1 4 -7
2 -3 8

7. Matrix Notation
Each row of the matrix corresponds to an equation and
each column corresponds to a variable except that the last
column corresponds to numbers.

8. Matrix Notation
Each row of the matrix corresponds to an equation and
each column corresponds to a variable except that the last
column corresponds to numbers. Operations of the
equations correspond to operations of rows in the matrices.
There’re three main operations.

9. Matrix Notation
Each row of the matrix corresponds to an equation and
each column corresponds to a variable except that the last
column corresponds to numbers. Operations of the
equations correspond to operations of rows in the matrices.
There’re three main operations.
The Three Row Operations for Matrices

10. Matrix Notation
Each row of the matrix corresponds to an equation and
each column corresponds to a variable except that the last
column corresponds to numbers. Operations of the
equations correspond to operations of rows in the matrices.
There’re three main operations.
The Three Row Operations for Matrices
I. Switching rows, notated as Row i Row j, or Ri Rj

11. Matrix Notation
Each row of the matrix corresponds to an equation and
each column corresponds to a variable except that the last
column corresponds to numbers. Operations of the
equations correspond to operations of rows in the matrices.
There’re three main operations.
The Three Row Operations for Matrices
I. Switching rows, notated as Row i Row j, or Ri Rj
For example,
1 4 -7
2 -3 8

12. Matrix Notation
Each row of the matrix corresponds to an equation and
each column corresponds to a variable except that the last
column corresponds to numbers. Operations of the
equations correspond to operations of rows in the matrices.
There’re three main operations.
The Three Row Operations for Matrices
I. Switching rows, notated as Row i Row j, or Ri Rj
For example,
1 4 -7 R1 R2 2 -3 8
2 -3 8 1 4 -7

13. Matrix Notation
Each row of the matrix corresponds to an equation and
each column corresponds to a variable except that the last
column corresponds to numbers. Operations of the
equations correspond to operations of rows in the matrices.
There’re three main operations.
The Three Row Operations for Matrices
I. Switching rows, notated as Row i Row j, or Ri Rj
For example,
1 4 -7 R1 R2 2 -3 8
2 -3 8 1 4 -7
II. Multiply Row i by a nonzero constant k, notated as k*Ri.

14. Matrix Notation
Each row of the matrix corresponds to an equation and
each column corresponds to a variable except that the last
column corresponds to numbers. Operations of the
equations correspond to operations of rows in the matrices.
There’re three main operations.
The Three Row Operations for Matrices
I. Switching rows, notated as Row i Row j, or Ri Rj
For example,
1 4 -7 R1 R2 2 -3 8
2 -3 8 1 4 -7
II. Multiply Row i by a nonzero constant k, notated as k*Ri.
For example:
1 4 -7
2 -3 8

15. Matrix Notation
Each row of the matrix corresponds to an equation and
each column corresponds to a variable except that the last
column corresponds to numbers. Operations of the
equations correspond to operations of rows in the matrices.
There’re three main operations.
The Three Row Operations for Matrices
I. Switching rows, notated as Row i Row j, or Ri Rj
For example,
1 4 -7 R1 R2 2 -3 8
2 -3 8 1 4 -7
II. Multiply Row i by a nonzero constant k, notated as k*Ri.
For example:
1 4 -7 -3*R2
2 -3 8

16. Matrix Notation
Each row of the matrix corresponds to an equation and
each column corresponds to a variable except that the last
column corresponds to numbers. Operations of the
equations correspond to operations of rows in the matrices.
There’re three main operations.
The Three Row Operations for Matrices
I. Switching rows, notated as Row i Row j, or Ri Rj
For example,
1 4 -7 R1 R2 2 -3 8
2 -3 8 1 4 -7
II. Multiply Row i by a nonzero constant k, notated as k*Ri.
For example:
1 4 -7 1 4 -7
-3*R2
2 -3 8 -6 9 -24

17. Matrix Notation
III. Add the multiple of row on top of another row, notated as
“k*Ri add  Rj”.

18. Matrix Notation
III. Add the multiple of row on top of another row, notated as
“k*Ri add  Rj”.
For example,
1 4 -7
2 -3 8

19. Matrix Notation
III. Add the multiple of row on top of another row, notated as
“k*Ri add  Rj”.
For example,
1 4 -7 -2*R1 add  R2
2 -3 8

20. Matrix Notation
III. Add the multiple of row on top of another row, notated as
“k*Ri add  Rj”.
For example, write a copy of -2*R1
-2 -8 14
1 4 -7 -2*R1 add  R2
2 -3 8

21. Matrix Notation
III. Add the multiple of row on top of another row, notated as
“k*Ri add  Rj”.
For example, write a copy of -2*R1
-2 -8 14
1 4 -7 -2*R1 add  R2 1 4 -7
2 -3 8 0 -11 22

22. Matrix Notation
III. Add the multiple of row on top of another row, notated as
“k*Ri add  Rj”.
For example, write a copy of -2*R1
-2 -8 14
1 4 -7 -2*R1 add  R2 1 4 -7
2 -3 8 0 -11 22
Fact: Performing row operations on a matrix does not change
the solution of the system.

23. Matrix Notation
III. Add the multiple of row on top of another row, notated as
“k*Ri add  Rj”.
For example, write a copy of -2*R1
-2 -8 14
1 4 -7 -2*R1 add  R2 1 4 -7
2 -3 8 0 -11 22
Fact: Performing row operations on a matrix does not change
the solution of the system.
Elimination Method in Matrix Notation

24. Matrix Notation
III. Add the multiple of row on top of another row, notated as
“k*Ri add  Rj”.
For example, write a copy of -2*R1
-2 -8 14
1 4 -7 -2*R1 add  R2 1 4 -7
2 -3 8 0 -11 22
Fact: Performing row operations on a matrix does not change
the solution of the system.
Elimination Method in Matrix Notation
• Apply row operations to transform the matrix to the upper
diagonal form where all the entries below the main diagonal
(the lower left triangular region) are 0.

25. Matrix Notation
III. Add the multiple of row on top of another row, notated as
“k*Ri add  Rj”.
For example, write a copy of -2*R1
-2 -8 14
1 4 -7 -2*R1 add  R2 1 4 -7
2 -3 8 0 -11 22
Fact: Performing row operations on a matrix does not change
the solution of the system.
Elimination Method in Matrix Notation
• Apply row operations to transform the matrix to the upper
diagonal form where all the entries below the main diagonal
(the lower left triangular region) are 0.
* * * *
* * * *
* * * *

26. Matrix Notation
III. Add the multiple of row on top of another row, notated as
“k*Ri add  Rj”.
For example, write a copy of -2*R1
-2 -8 14
1 4 -7 -2*R1 add  R2 1 4 -7
2 -3 8 0 -11 22
Fact: Performing row operations on a matrix does not change
the solution of the system.
Elimination Method in Matrix Notation
• Apply row operations to transform the matrix to the upper
diagonal form where all the entries below the main diagonal
(the lower left triangular region) are 0.
* * * * Row operations
* * * *
* * * *

27. Matrix Notation
III. Add the multiple of row on top of another row, notated as
“k*Ri add  Rj”.
For example, write a copy of -2*R1
-2 -8 14
1 4 -7 -2*R1 add  R2 1 4 -7
2 -3 8 0 -11 22
Fact: Performing row operations on a matrix does not change
the solution of the system.
Elimination Method in Matrix Notation
• Apply row operations to transform the matrix to the upper
diagonal form where all the entries below the main diagonal
(the lower left triangular region) are 0.
* * * * Row operations * * * *
* * * * 0
0
* * *
0
* * * * * *

28. Matrix Notation
2. Starting from the bottom row, get the answer for one of the
variable.

29. Matrix Notation
2. Starting from the bottom row, get the answer for one of the
variable. Then go up one row, using the solution already
obtained to get another answer of another variable.

30. Matrix Notation
2. Starting from the bottom row, get the answer for one of the
variable. Then go up one row, using the solution already
obtained to get another answer of another variable. Repeat
the process, working up the rows to extract all solutions.

31. Matrix Notation
2. Starting from the bottom row, get the answer for one of the
variable. Then go up one row, using the solution already
obtained to get another answer of another variable. Repeat
the process, working up the rows to extract all solutions.
Example A. Solve using matrix notation.
x + 4y = -7 Eq. 1
{ 2x – 3y = 8 Eq. 2

32. Matrix Notation
2. Starting from the bottom row, get the answer for one of the
variable. Then go up one row, using the solution already
obtained to get another answer of another variable. Repeat
the process, working up the rows to extract all solutions.
Example A. Solve using matrix notation.
x + 4y = -7 Eq. 1
{ 2x – 3y = 8 Eq. 2
Put the system into a matrix:

33. Matrix Notation
2. Starting from the bottom row, get the answer for one of the
variable. Then go up one row, using the solution already
obtained to get another answer of another variable. Repeat
the process, working up the rows to extract all solutions.
Example A. Solve using matrix notation.
x + 4y = -7 Eq. 1
{ 2x – 3y = 8 Eq. 2
Put the system into a matrix:
1 4 -7
2 -3 8

34. Matrix Notation
2. Starting from the bottom row, get the answer for one of the
variable. Then go up one row, using the solution already
obtained to get another answer of another variable. Repeat
the process, working up the rows to extract all solutions.
Example A. Solve using matrix notation.
x + 4y = -7 Eq. 1
{ 2x – 3y = 8 Eq. 2
Put the system into a matrix:
1 4 -7
2 -3 8

35. Matrix Notation
2. Starting from the bottom row, get the answer for one of the
variable. Then go up one row, using the solution already
obtained to get another answer of another variable. Repeat
the process, working up the rows to extract all solutions.
Example A. Solve using matrix notation.
x + 4y = -7 Eq. 1
{ 2x – 3y = 8 Eq. 2
Put the system into a matrix:
1 4 -7 -2*R1 add  R2
2 -3 8

36. Matrix Notation
2. Starting from the bottom row, get the answer for one of the
variable. Then go up one row, using the solution already
obtained to get another answer of another variable. Repeat
the process, working up the rows to extract all solutions.
Example A. Solve using matrix notation.
x + 4y = -7 Eq. 1
{ 2x – 3y = 8 Eq. 2
Put the system into a matrix:
-2 -8 14
1 4 -7 -2*R1 add  R2
2 -3 8

37. Matrix Notation
2. Starting from the bottom row, get the answer for one of the
variable. Then go up one row, using the solution already
obtained to get another answer of another variable. Repeat
the process, working up the rows to extract all solutions.
Example A. Solve using matrix notation.
x + 4y = -7 Eq. 1
{ 2x – 3y = 8 Eq. 2
Put the system into a matrix:
-2 -8 14
1 4 -7 -2*R1 add  R2 1 4 -7
2 -3 8 0 -11 22

38. Matrix Notation
2. Starting from the bottom row, get the answer for one of the
variable. Then go up one row, using the solution already
obtained to get another answer of another variable. Repeat
the process, working up the rows to extract all solutions.
Example A. Solve using matrix notation.
x + 4y = -7 Eq. 1
{ 2x – 3y = 8 Eq. 2
Put the system into a matrix:
-2 -8 14
1 4 -7 -2*R1 add  R2 1 4 -7
2 -3 8 0 -11 22
From the bottom R2: -11y = 22  y = -2

39. Matrix Notation
2. Starting from the bottom row, get the answer for one of the
variable. Then go up one row, using the solution already
obtained to get another answer of another variable. Repeat
the process, working up the rows to extract all solutions.
Example A. Solve using matrix notation.
x + 4y = -7 Eq. 1
{ 2x – 3y = 8 Eq. 2
Put the system into a matrix:
-2 -8 14
1 4 -7 -2*R1 add  R2 1 4 -7
2 -3 8 0 -11 22
From the bottom R2: -11y = 22  y = -2
Go up one row to R1 and set y = -2:

40. Matrix Notation
2. Starting from the bottom row, get the answer for one of the
variable. Then go up one row, using the solution already
obtained to get another answer of another variable. Repeat
the process, working up the rows to extract all solutions.
Example A. Solve using matrix notation.
x + 4y = -7 Eq. 1
{ 2x – 3y = 8 Eq. 2
Put the system into a matrix:
-2 -8 14
1 4 -7 -2*R1 add  R2 1 4 -7
2 -3 8 0 -11 22
From the bottom R2: -11y = 22  y = -2
Go up one row to R1 and set y = -2:
x + 4y = -7

41. Matrix Notation
2. Starting from the bottom row, get the answer for one of the
variable. Then go up one row, using the solution already
obtained to get another answer of another variable. Repeat
the process, working up the rows to extract all solutions.
Example A. Solve using matrix notation.
x + 4y = -7 Eq. 1
{ 2x – 3y = 8 Eq. 2
Put the system into a matrix:
-2 -8 14
1 4 -7 -2*R1 add  R2 1 4 -7
2 -3 8 0 -11 22
From the bottom R2: -11y = 22  y = -2
Go up one row to R1 and set y = -2:
x + 4y = -7
x + 4(-2) = -7

42. Matrix Notation
2. Starting from the bottom row, get the answer for one of the
variable. Then go up one row, using the solution already
obtained to get another answer of another variable. Repeat
the process, working up the rows to extract all solutions.
Example A. Solve using matrix notation.
x + 4y = -7 Eq. 1
{ 2x – 3y = 8 Eq. 2
Put the system into a matrix:
-2 -8 14
1 4 -7 -2*R1 add  R2 1 4 -7
2 -3 8 0 -11 22
From the bottom R2: -11y = 22  y = -2
Go up one row to R1 and set y = -2:
x + 4y = -7
x + 4(-2) = -7
x=1 Solution : (1, -2)

43. Matrix Notation
Example B. Solve using matrix notation.
E1
{
2x + 3y + 3z = 13
x + 2y + 2z = 8 E2
3x + 2y + 3z = 13 E3

44. Matrix Notation
Example B. Solve using matrix notation.
E1
{
2x + 3y + 3z = 13
x + 2y + 2z = 8 E2
3x + 2y + 3z = 13 E3
Put the system into a matrix:

45. Matrix Notation
Example B. Solve using matrix notation.
E1
{
2x + 3y + 3z = 13
x + 2y + 2z = 8 E2
3x + 2y + 3z = 13 E3
Put the system into a matrix:
2 3 3 13
1 2 2 8
3 2 3 13

46. Matrix Notation
Example B. Solve using matrix notation.
E1
{
2x + 3y + 3z = 13
x + 2y + 2z = 8 E2
3x + 2y + 3z = 13 E3
Put the system into a matrix:
2 3 3 13 R1 R2
1 2 2 8
3 2 3 13

47. Matrix Notation
Example B. Solve using matrix notation.
E1
{
2x + 3y + 3z = 13
x + 2y + 2z = 8 E2
3x + 2y + 3z = 13 E3
Put the system into a matrix:
2 3 3 13 R1 R2 1 2 2 8
1 2 2 8 2 3 3 13
3 2 3 13 3 2 3 13

48. Matrix Notation
Example B. Solve using matrix notation.
E1
{
2x + 3y + 3z = 13
x + 2y + 2z = 8 E2
3x + 2y + 3z = 13 E3
Put the system into a matrix:
2 3 3 13 R1 R2 1 2 2 8
1 2 2 8 2 3 3 13
3 2 3 13 3 2 3 13
-2R1 add R2

49. Matrix Notation
Example B. Solve using matrix notation.
E1
{
2x + 3y + 3z = 13
x + 2y + 2z = 8 E2
3x + 2y + 3z = 13 E3
Put the system into a matrix:
-2 -4 -4 -16
2 3 3 13 R1 R2 1 2 2 8
1 2 2 8 2 3 3 13
3 2 3 13 3 2 3 13
-2R1 add R2

50. Matrix Notation
Example B. Solve using matrix notation.
E1
{
2x + 3y + 3z = 13
x + 2y + 2z = 8 E2
3x + 2y + 3z = 13 E3
Put the system into a matrix:
-2 -4 -4 -16
2 3 3 13 R1 R2 1 2 2 8
1 2 2 8 2 3 3 13
3 2 3 13 3 2 3 13
-2R1 add R2
1 2 2 8
0 -1 -1 -3
3 2 3 13

51. Matrix Notation
Example B. Solve using matrix notation.
E1
{
2x + 3y + 3z = 13
x + 2y + 2z = 8 E2
3x + 2y + 3z = 13 E3
Put the system into a matrix:
-2 -4 -4 -16
2 3 3 13 R1 R2 1 2 2 8
1 2 2 8 2 3 3 13
3 2 3 13 3 2 3 13
-2R1 add R2
1 2 2 8
0 -1 -1 -3 -3* R1 add R3
3 2 3 13

52. Matrix Notation
Example B. Solve using matrix notation.
E1
{
2x + 3y + 3z = 13
x + 2y + 2z = 8 E2
3x + 2y + 3z = 13 E3
Put the system into a matrix:
-2 -4 -4 -16
2 3 3 13 R1 R2 1 2 2 8
1 2 2 8 2 3 3 13
3 2 3 13 3 2 3 13
-3 -6 -6 -24 -2R1 add R2
1 2 2 8
0 -1 -1 -3 -3* R1 add R3
3 2 3 13

53. Matrix Notation
Example B. Solve using matrix notation.
E1
{
2x + 3y + 3z = 13
x + 2y + 2z = 8 E2
3x + 2y + 3z = 13 E3
Put the system into a matrix:
-2 -4 -4 -16
2 3 3 13 R1 R2 1 2 2 8
1 2 2 8 2 3 3 13
3 2 3 13 3 2 3 13
-3 -6 -6 -24 -2R1 add R2
1 2 2 8 1 2 2 8
0 -1 -1 -3 -3* R1 add R3 0 -1 -1 -3
3 2 3 13 0 -4 -3 -11

54. Matrix Notation
Example B. Solve using matrix notation.
E1
{
2x + 3y + 3z = 13
x + 2y + 2z = 8 E2
3x + 2y + 3z = 13 E3
Put the system into a matrix:
-2 -4 -4 -16
2 3 3 13 R1 R2 1 2 2 8
1 2 2 8 2 3 3 13
3 2 3 13 3 2 3 13
-3 -6 -6 -24 -2R1 add R2
1 2 2 8 1 2 2 8
0 -1 -1 -3 -3* R1 add R3 0 -1 -1 -3
3 2 3 13 0 -4 -3 -11
-4*R2 add R3

55. Matrix Notation
Example B. Solve using matrix notation.
E1
{
2x + 3y + 3z = 13
x + 2y + 2z = 8 E2
3x + 2y + 3z = 13 E3
Put the system into a matrix:
-2 -4 -4 -16
2 3 3 13 R1 R2 1 2 2 8
1 2 2 8 2 3 3 13
3 2 3 13 3 2 3 13
-3 -6 -6 -24 -2R1 add R2
1 2 2 8 1 0
24 2
4 12
8
0 -1 -1 -3 -3* R1 add R3 0 -1 -1 -3
3 2 3 13 0 -4 -3 -11
-4*R2 add R3

56. Matrix Notation
Example B. Solve using matrix notation.
E1
{
2x + 3y + 3z = 13
x + 2y + 2z = 8 E2
3x + 2y + 3z = 13 E3
Put the system into a matrix:
-2 -4 -4 -16
2 3 3 13 R1 R2 1 2 2 8
1 2 2 8 2 3 3 13
3 2 3 13 3 2 3 13
-3 -6 -6 -24 -2R1 add R2
1 2 2 8 1 0
24 2
4 12
8
0 -1 -1 -3 -3* R1 add R3 0 -1 -1 -3
3 2 3 13 0 -4 -3 -11
1 2 2 8 -4*R2 add R3
0 -1 -1 -3
0 0 1 1

57. Matrix Notation
Example B. Solve using matrix notation.
E1
{
2x + 3y + 3z = 13
x + 2y + 2z = 8 E2
3x + 2y + 3z = 13 E3
Put the system into a matrix:
-2 -4 -4 -16
2 3 3 13 R1 R2 1 2 2 8
1 2 2 8 2 3 3 13
3 2 3 13 3 2 3 13
-3 -6 -6 -24 -2R1 add R2
1 2 2 8 1 0 2 4 2 12
4
8
0 -1 -1 -3 -3* R1 add R3 0 -1 -1 -3
3 2 3 13 0 -4 -3 -11
1 2 2 8 -4*R2 add R3
0 -1 -1 -3
0 0 1 1 It's in upper diagonal form. Ready to solve.

58. Matrix Notation
We have reduced the matrix.
2 3 3 13 1 2 2 8
1 2 2 8 0 -1 -1 -3
3 2 3 13 0 0 1 1

59. Matrix Notation
We have reduced the matrix.
2 3 3 13 1 2 2 8
1 2 2 8 0 -1 -1 -3
3 2 3 13 0 0 1 1
From R3, we get z = 1.

60. Matrix Notation
We have reduced the matrix.
2 3 3 13 1 2 2 8
1 2 2 8 0 -1 -1 -3
3 2 3 13 0 0 1 1
From R3, we get z = 1.
From R2, -y – z = -3

61. Matrix Notation
We have reduced the matrix.
2 3 3 13 1 2 2 8
1 2 2 8 0 -1 -1 -3
3 2 3 13 0 0 1 1
From R3, we get z = 1.
From R2, -y – z = -3
-y – (1) = -3

62. Matrix Notation
We have reduced the matrix.
2 3 3 13 1 2 2 8
1 2 2 8 0 -1 -1 -3
3 2 3 13 0 0 1 1
From R3, we get z = 1.
From R2, -y – z = -3
-y – (1) = -3
3–1=y
2=y

63. Matrix Notation
We have reduced the matrix.
2 3 3 13 1 2 2 8
1 2 2 8 0 -1 -1 -3
3 2 3 13 0 0 1 1
From R3, we get z = 1,
From R2, -y – z = -3
-y – (1) = -3
3–1=y
2=y
From R1, we get
x + 2y + 2z = 8

64. Matrix Notation
We have reduced the matrix.
2 3 3 13 1 2 2 8
1 2 2 8 0 -1 -1 -3
3 2 3 13 0 0 1 1
From R3, we get z = 1,
From R2, -y – z = -3
-y – (1) = -3
3–1=y
2=y
From R1, we get
x + 2y + 2z = 8
x + 2(2) + 2(1) = 8

65. Matrix Notation
We have reduced the matrix.
2 3 3 13 1 2 2 8
1 2 2 8 0 -1 -1 -3
3 2 3 13 0 0 1 1
From R3, we get z = 1,
From R2, -y – z = -3
-y – (1) = -3
3–1=y
2=y
From R1, we get
x + 2y + 2z = 8
x + 2(2) + 2(1) = 8
x+6=8

66. Matrix Notation
We have reduced the matrix.
2 3 3 13 1 2 2 8
1 2 2 8 0 -1 -1 -3
3 2 3 13 0 0 1 1
From R3, we get z = 1,
From R2, -y – z = -3
-y – (1) = -3
3–1=y
2=y
From R1, we get
x + 2y + 2z = 8
x + 2(2) + 2(1) = 8
x+6=8
x=2
So the solution is (2, 2, 1)