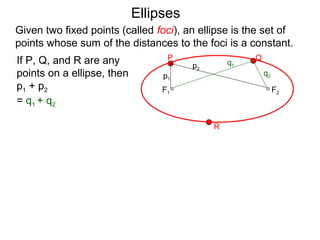
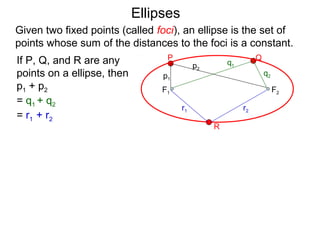
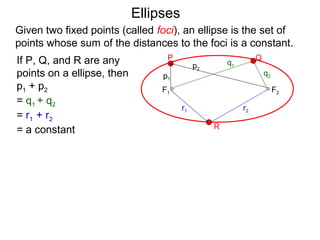
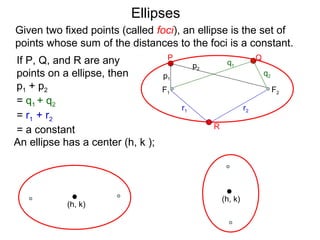
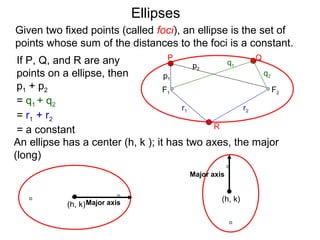
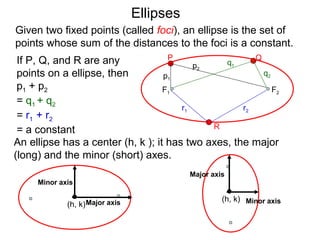
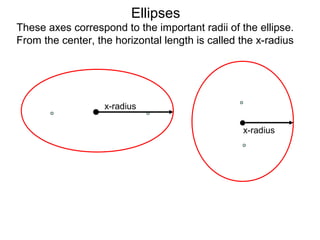
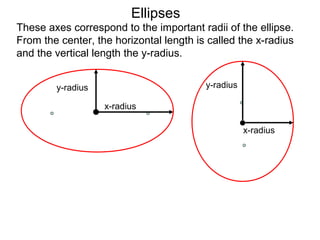
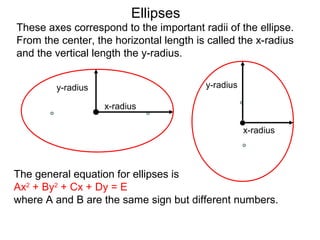
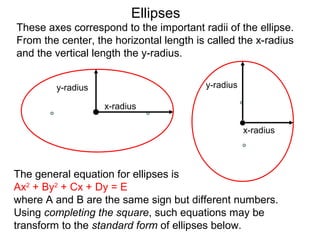
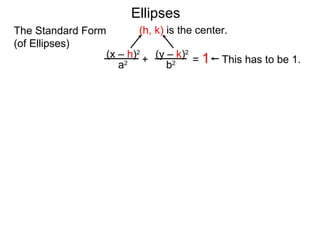
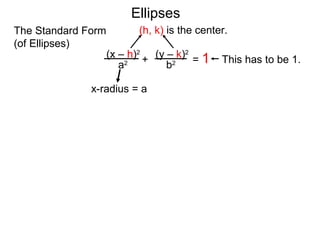
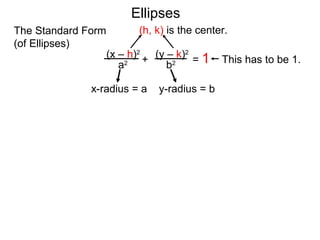
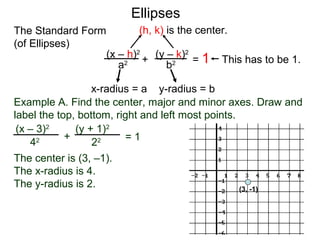
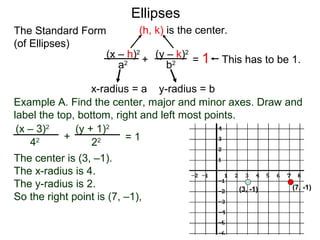
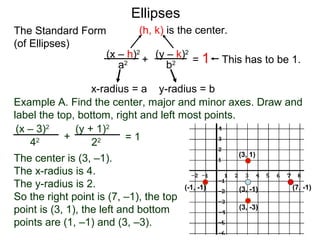
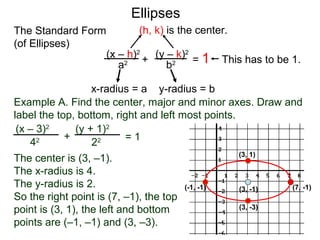
The document defines and describes ellipses. It states that an ellipse is the set of points whose sum of the distances to two fixed foci is a constant. An ellipse has a center, major axis, and minor axis. The standard form of the ellipse equation is given as (x-h)2/a2 + (y-k)2/b2 = 1, where (h,k) is the center, a is the x-radius, and b is the y-radius. An example problem demonstrates how to identify these properties from a given ellipse equation and sketch the ellipse.

1. Ellipses

2. Ellipses
Given two fixed points (called foci), an ellipse is the set of
points whose sum of the distances to the foci is a constant.

3. F2F1
Ellipses
Given two fixed points (called foci), an ellipse is the set of
points whose sum of the distances to the foci is a constant.

4. F2F1
P Q
R
If P, Q, and R are any
points on a ellipse,
Ellipses
Given two fixed points (called foci), an ellipse is the set of
points whose sum of the distances to the foci is a constant.

5. F2F1
P Q
R
p1
p2
If P, Q, and R are any
points on a ellipse, then
p1 + p2
Ellipses
Given two fixed points (called foci), an ellipse is the set of
points whose sum of the distances to the foci is a constant.

6. F2F1
P Q
R
p1
p2
If P, Q, and R are any
points on a ellipse, then
p1 + p2
= q1 + q2
q1
q2
Ellipses
Given two fixed points (called foci), an ellipse is the set of
points whose sum of the distances to the foci is a constant.

7. F2F1
P Q
R
p1
p2
If P, Q, and R are any
points on a ellipse, then
p1 + p2
= q1 + q2
= r1 + r2
q1
q2
r2r1
Ellipses
Given two fixed points (called foci), an ellipse is the set of
points whose sum of the distances to the foci is a constant.

8. F2F1
P Q
R
p1
p2
If P, Q, and R are any
points on a ellipse, then
p1 + p2
= q1 + q2
= r1 + r2
= a constant
q1
q2
r2r1
Ellipses
Given two fixed points (called foci), an ellipse is the set of
points whose sum of the distances to the foci is a constant.

9. F2F1
P Q
R
p1
p2
If P, Q, and R are any
points on a ellipse, then
p1 + p2
= q1 + q2
= r1 + r2
= a constant
q1
q2
r2r1
Ellipses
An ellipse has a center (h, k );
(h, k)
(h, k)
Given two fixed points (called foci), an ellipse is the set of
points whose sum of the distances to the foci is a constant.

10. F2F1
P Q
R
p1
p2
If P, Q, and R are any
points on a ellipse, then
p1 + p2
= q1 + q2
= r1 + r2
= a constant
q1
q2
r2r1
Ellipses
An ellipse has a center (h, k ); it has two axes, the major
(long)
(h, k)
(h, k)
Given two fixed points (called foci), an ellipse is the set of
points whose sum of the distances to the foci is a constant.
Major axis
Major axis

11. F2F1
P Q
R
p1
p2
If P, Q, and R are any
points on a ellipse, then
p1 + p2
= q1 + q2
= r1 + r2
= a constant
q1
q2
r2r1
Ellipses
An ellipse has a center (h, k ); it has two axes, the major
(long) and the minor (short) axes.
(h, k)Major axis
Minor axis
(h, k)
Major axis
Minor axis
Given two fixed points (called foci), an ellipse is the set of
points whose sum of the distances to the foci is a constant.

12. These axes correspond to the important radii of the ellipse.
Ellipses

13. These axes correspond to the important radii of the ellipse.
From the center, the horizontal length is called the x-radius
Ellipses
x-radius
x-radius

14. y-radius
These axes correspond to the important radii of the ellipse.
From the center, the horizontal length is called the x-radius
and the vertical length the y-radius.
Ellipses
x-radius
x-radius
y-radius

15. These axes correspond to the important radii of the ellipse.
From the center, the horizontal length is called the x-radius
and the vertical length the y-radius.
Ellipses
x-radius
The general equation for ellipses is
Ax2
+ By2
+ Cx + Dy = E
where A and B are the same sign but different numbers.
x-radius
y-radiusy-radius

16. These axes correspond to the important radii of the ellipse.
From the center, the horizontal length is called the x-radius
and the vertical length the y-radius.
Ellipses
x-radius
The general equation for ellipses is
Ax2
+ By2
+ Cx + Dy = E
where A and B are the same sign but different numbers.
Using completing the square, such equations may be
transform to the standard form of ellipses below.
x-radius
y-radiusy-radius

17. (x – h)2
(y – k)2
a2
b2
Ellipses
+ = 1
The Standard Form
(of Ellipses)

18. (x – h)2
(y – k)2
a2
b2
Ellipses
+ = 1 This has to be 1.
The Standard Form
(of Ellipses)

19. (x – h)2
(y – k)2
a2
b2
(h, k) is the center.
Ellipses
+ = 1 This has to be 1.
The Standard Form
(of Ellipses)

20. (x – h)2
(y – k)2
a2
b2
x-radius = a
(h, k) is the center.
Ellipses
+ = 1 This has to be 1.
The Standard Form
(of Ellipses)

21. (x – h)2
(y – k)2
a2
b2
x-radius = a y-radius = b
(h, k) is the center.
Ellipses
+ = 1 This has to be 1.
The Standard Form
(of Ellipses)

22. (x – h)2
(y – k)2
a2
b2
x-radius = a y-radius = b
(h, k) is the center.
Ellipses
+ = 1 This has to be 1.
Example A. Find the center, major and minor axes. Draw and
label the top, bottom, right and left most points.
(x – 3)2
(y + 1)2
42
22+ = 1
The Standard Form
(of Ellipses)

23. (x – h)2
(y – k)2
a2
b2
x-radius = a y-radius = b
(h, k) is the center.
Ellipses
+ = 1 This has to be 1.
Example A. Find the center, major and minor axes. Draw and
label the top, bottom, right and left most points.
(x – 3)2
(y + 1)2
42
22+ = 1
The center is (3, –1).
The Standard Form
(of Ellipses)

24. (x – h)2
(y – k)2
a2
b2
x-radius = a y-radius = b
(h, k) is the center.
Ellipses
+ = 1 This has to be 1.
Example A. Find the center, major and minor axes. Draw and
label the top, bottom, right and left most points.
(x – 3)2
(y + 1)2
42
22+ = 1
The center is (3, –1).
The x-radius is 4.
The Standard Form
(of Ellipses)

25. (x – h)2
(y – k)2
a2
b2
x-radius = a y-radius = b
(h, k) is the center.
Ellipses
+ = 1 This has to be 1.
Example A. Find the center, major and minor axes. Draw and
label the top, bottom, right and left most points.
(x – 3)2
(y + 1)2
42
22+ = 1
The center is (3, –1).
The x-radius is 4.
The y-radius is 2.
The Standard Form
(of Ellipses)

26. (x – h)2
(y – k)2
a2
b2
x-radius = a y-radius = b
(h, k) is the center.
Ellipses
+ = 1 This has to be 1.
(3, -1)
Example A. Find the center, major and minor axes. Draw and
label the top, bottom, right and left most points.
(x – 3)2
(y + 1)2
42
22+ = 1
The center is (3, –1).
The x-radius is 4.
The y-radius is 2.
The Standard Form
(of Ellipses)

27. (x – h)2
(y – k)2
a2
b2
x-radius = a y-radius = b
(h, k) is the center.
Ellipses
+ = 1 This has to be 1.
(3, -1) (7, -1)
Example A. Find the center, major and minor axes. Draw and
label the top, bottom, right and left most points.
(x – 3)2
(y + 1)2
42
22+ = 1
The center is (3, –1).
The x-radius is 4.
The y-radius is 2.
So the right point is (7, –1),
The Standard Form
(of Ellipses)

28. (x – h)2
(y – k)2
a2
b2
x-radius = a y-radius = b
(h, k) is the center.
Ellipses
+ = 1 This has to be 1.
(3, -1) (7, -1)
(3, 1)
Example A. Find the center, major and minor axes. Draw and
label the top, bottom, right and left most points.
(x – 3)2
(y + 1)2
42
22+ = 1
The center is (3, –1).
The x-radius is 4.
The y-radius is 2.
So the right point is (7, –1), the top
point is (3, 1),
The Standard Form
(of Ellipses)

29. (x – h)2
(y – k)2
a2
b2
x-radius = a y-radius = b
(h, k) is the center.
Ellipses
+ = 1 This has to be 1.
(3, -1) (7, -1)(-1, -1)
(3, -3)
(3, 1)
Example A. Find the center, major and minor axes. Draw and
label the top, bottom, right and left most points.
(x – 3)2
(y + 1)2
42
22+ = 1
The center is (3, –1).
The x-radius is 4.
The y-radius is 2.
So the right point is (7, –1), the top
point is (3, 1), the left and bottom
points are (1, –1) and (3, –3).
The Standard Form
(of Ellipses)

30. (x – h)2
(y – k)2
a2
b2
x-radius = a y-radius = b
(h, k) is the center.
Ellipses
+ = 1 This has to be 1.
(3, -1) (7, -1)(-1, -1)
(3, -3)
(3, 1)
Example A. Find the center, major and minor axes. Draw and
label the top, bottom, right and left most points.
(x – 3)2
(y + 1)2
42
22+ = 1
The center is (3, –1).
The x-radius is 4.
The y-radius is 2.
So the right point is (7, –1), the top
point is (3, 1), the left and bottom
points are (–1, –1) and (3, –3).
The Standard Form
(of Ellipses)

31. Example B. Put 9x2
+ 4y2
– 18x – 16y = 11 into the
standard form. Find the center, major and minor axis.
Draw and label the top, bottom, right, left most points.
Ellipses

32. Example B. Put 9x2
+ 4y2
– 18x – 16y = 11 into the
standard form. Find the center, major and minor axis.
Draw and label the top, bottom, right, left most points.
Group the x’s and the y’s:
Ellipses

33. Example B. Put 9x2
+ 4y2
– 18x – 16y = 11 into the
standard form. Find the center, major and minor axis.
Draw and label the top, bottom, right, left most points.
Group the x’s and the y’s:
9x2
– 18x + 4y2
– 16y = 11
Ellipses

34. Example B. Put 9x2
+ 4y2
– 18x – 16y = 11 into the
standard form. Find the center, major and minor axis.
Draw and label the top, bottom, right, left most points.
Group the x’s and the y’s:
9x2
– 18x + 4y2
– 16y = 11 factor out the square-coefficients
9(x2
– 2x ) + 4(y2
– 4y ) = 11
Ellipses

35. Example B. Put 9x2
+ 4y2
– 18x – 16y = 11 into the
standard form. Find the center, major and minor axis.
Draw and label the top, bottom, right, left most points.
Group the x’s and the y’s:
9x2
– 18x + 4y2
– 16y = 11 factor out the square-coefficients
9(x2
– 2x ) + 4(y2
– 4y ) = 11 complete the square
Ellipses

36. Example B. Put 9x2
+ 4y2
– 18x – 16y = 11 into the
standard form. Find the center, major and minor axis.
Draw and label the top, bottom, right, left most points.
Group the x’s and the y’s:
9x2
– 18x + 4y2
– 16y = 11 factor out the square-coefficients
9(x2
– 2x ) + 4(y2
– 4y ) = 11 complete the square
9(x2
– 2x + 1 ) + 4(y2
– 4y + 4 ) = 11
Ellipses

37. Example B. Put 9x2
+ 4y2
– 18x – 16y = 11 into the
standard form. Find the center, major and minor axis.
Draw and label the top, bottom, right, left most points.
Group the x’s and the y’s:
9x2
– 18x + 4y2
– 16y = 11 factor out the square-coefficients
9(x2
– 2x ) + 4(y2
– 4y ) = 11 complete the square
9(x2
– 2x + 1 ) + 4(y2
– 4y + 4 ) = 11
+9
Ellipses

38. Example B. Put 9x2
+ 4y2
– 18x – 16y = 11 into the
standard form. Find the center, major and minor axis.
Draw and label the top, bottom, right, left most points.
Group the x’s and the y’s:
9x2
– 18x + 4y2
– 16y = 11 factor out the square-coefficients
9(x2
– 2x ) + 4(y2
– 4y ) = 11 complete the square
9(x2
– 2x + 1 ) + 4(y2
– 4y + 4 ) = 11
+9 +16
Ellipses

39. Example B. Put 9x2
+ 4y2
– 18x – 16y = 11 into the
standard form. Find the center, major and minor axis.
Draw and label the top, bottom, right, left most points.
Group the x’s and the y’s:
9x2
– 18x + 4y2
– 16y = 11 factor out the square-coefficients
9(x2
– 2x ) + 4(y2
– 4y ) = 11 complete the square
9(x2
– 2x + 1 ) + 4(y2
– 4y + 4 ) = 11 + 9 + 16
+9 +16
Ellipses

40. Example B. Put 9x2
+ 4y2
– 18x – 16y = 11 into the
standard form. Find the center, major and minor axis.
Draw and label the top, bottom, right, left most points.
Group the x’s and the y’s:
9x2
– 18x + 4y2
– 16y = 11 factor out the square-coefficients
9(x2
– 2x ) + 4(y2
– 4y ) = 11 complete the square
9(x2
– 2x + 1 ) + 4(y2
– 4y + 4 ) = 11 + 9 + 16
+9 +16
Ellipses
9(x – 1)2
+ 4(y – 2)2
= 36

41. 9(x – 1)2
4(y – 2)2
36 36
Example B. Put 9x2
+ 4y2
– 18x – 16y = 11 into the
standard form. Find the center, major and minor axis.
Draw and label the top, bottom, right, left most points.
Group the x’s and the y’s:
9x2
– 18x + 4y2
– 16y = 11 factor out the square-coefficients
9(x2
– 2x ) + 4(y2
– 4y ) = 11 complete the square
9(x2
– 2x + 1 ) + 4(y2
– 4y + 4 ) = 11 + 9 + 16
+9 +16
+ = 1
Ellipses
9(x – 1)2
+ 4(y – 2)2
= 36 divide by 36 to get 1

42. 9(x – 1)2
4(y – 2)2
36 4 36 9
Example B. Put 9x2
+ 4y2
– 18x – 16y = 11 into the
standard form. Find the center, major and minor axis.
Draw and label the top, bottom, right, left most points.
Group the x’s and the y’s:
9x2
– 18x + 4y2
– 16y = 11 factor out the square-coefficients
9(x2
– 2x ) + 4(y2
– 4y ) = 11 complete the square
9(x2
– 2x + 1 ) + 4(y2
– 4y + 4 ) = 11 + 9 + 16
+9 +16
+ = 1
Ellipses
9(x – 1)2
+ 4(y – 2)2
= 36 divide by 36 to get 1

43. 9(x – 1)2
4(y – 2)2
36 4 36 9
Example B. Put 9x2
+ 4y2
– 18x – 16y = 11 into the
standard form. Find the center, major and minor axis.
Draw and label the top, bottom, right, left most points.
Group the x’s and the y’s:
9x2
– 18x + 4y2
– 16y = 11 factor out the square-coefficients
9(x2
– 2x ) + 4(y2
– 4y ) = 11 complete the square
9(x2
– 2x + 1 ) + 4(y2
– 4y + 4 ) = 11 + 9 + 16
+9 +16
+ = 1
(x – 1)2
(y – 2)2
22
32
+ = 1
Ellipses
9(x – 1)2
+ 4(y – 2)2
= 36 divide by 36 to get 1

44. 9(x – 1)2
4(y – 2)2
36 4 36 9
Example B. Put 9x2
+ 4y2
– 18x – 16y = 11 into the
standard form. Find the center, major and minor axis.
Draw and label the top, bottom, right, left most points.
Group the x’s and the y’s:
9x2
– 18x + 4y2
– 16y = 11 factor out the square-coefficients
9(x2
– 2x ) + 4(y2
– 4y ) = 11 complete the square
9(x2
– 2x + 1 ) + 4(y2
– 4y + 4 ) = 11 + 9 + 16
+9 +16
+ = 1
(x – 1)2
(y – 2)2
22
32
+ = 1
Ellipses
9(x – 1)2
+ 4(y – 2)2
= 36 divide by 36 to get 1
Hence, Center: (1, 2),
x-radius is 2,
y-radius is 3.

45. 9(x – 1)2
4(y – 2)2
36 4 36 9
Example B. Put 9x2
+ 4y2
– 18x – 16y = 11 into the
standard form. Find the center, major and minor axis.
Draw and label the top, bottom, right, left most points.
Group the x’s and the y’s:
9x2
– 18x + 4y2
– 16y = 11 factor out the square-coefficients
9(x2
– 2x ) + 4(y2
– 4y ) = 11 complete the square
9(x2
– 2x + 1 ) + 4(y2
– 4y + 4 ) = 11 + 9 + 16
+9 +16
+ = 1
(x – 1)2
(y – 2)2
22
32
+ = 1
Ellipses
9(x – 1)2
+ 4(y – 2)2
= 36 divide by 36 to get 1
Hence, Center: (1, 2),
x-radius is 2,
y-radius is 3.
(-1, 2) (3, 2)
(1, 5)
(1, -1)
(1, 2)

46. Ellipses

47. Ellipses

48. Ellipses (Answers)