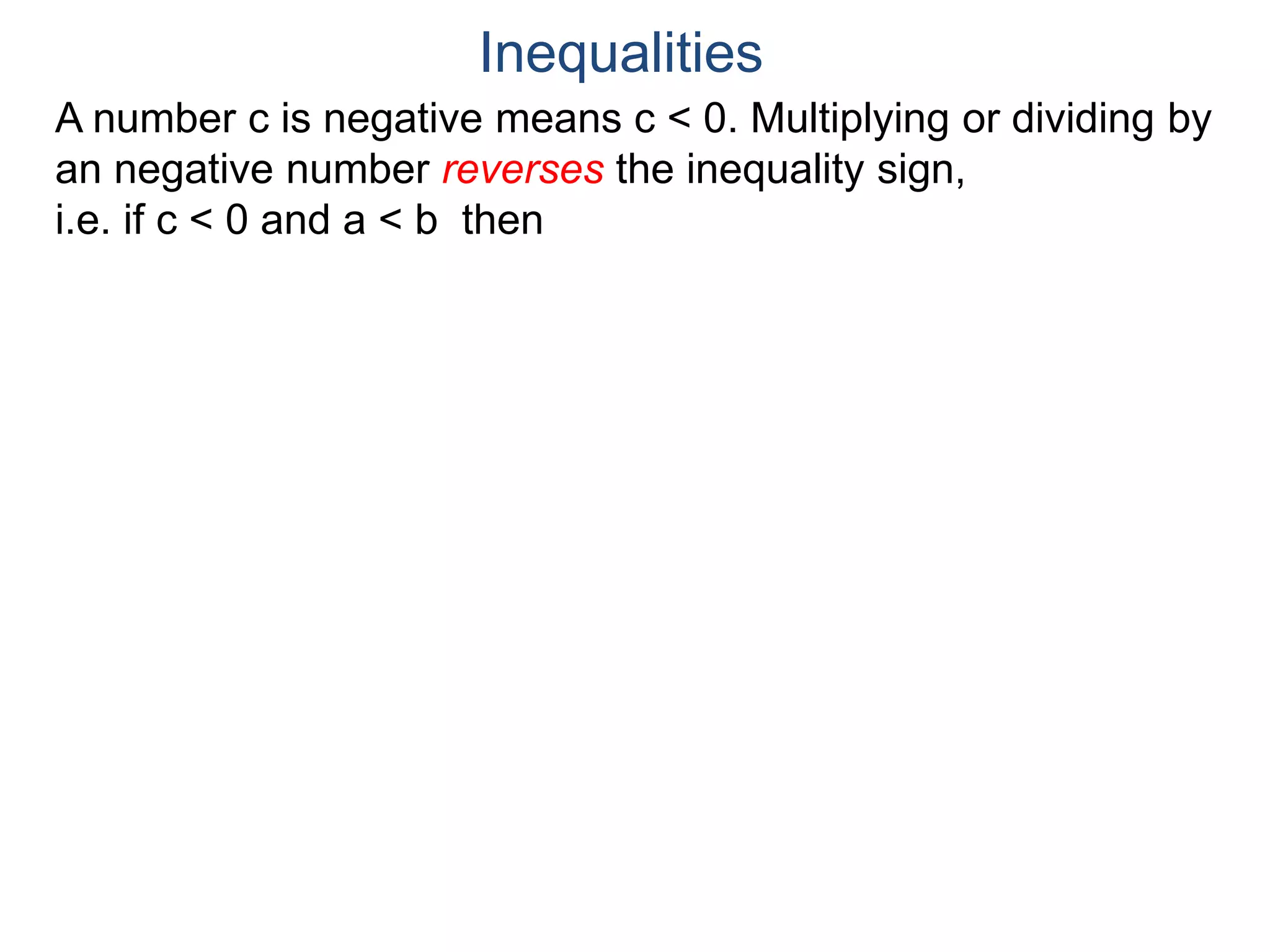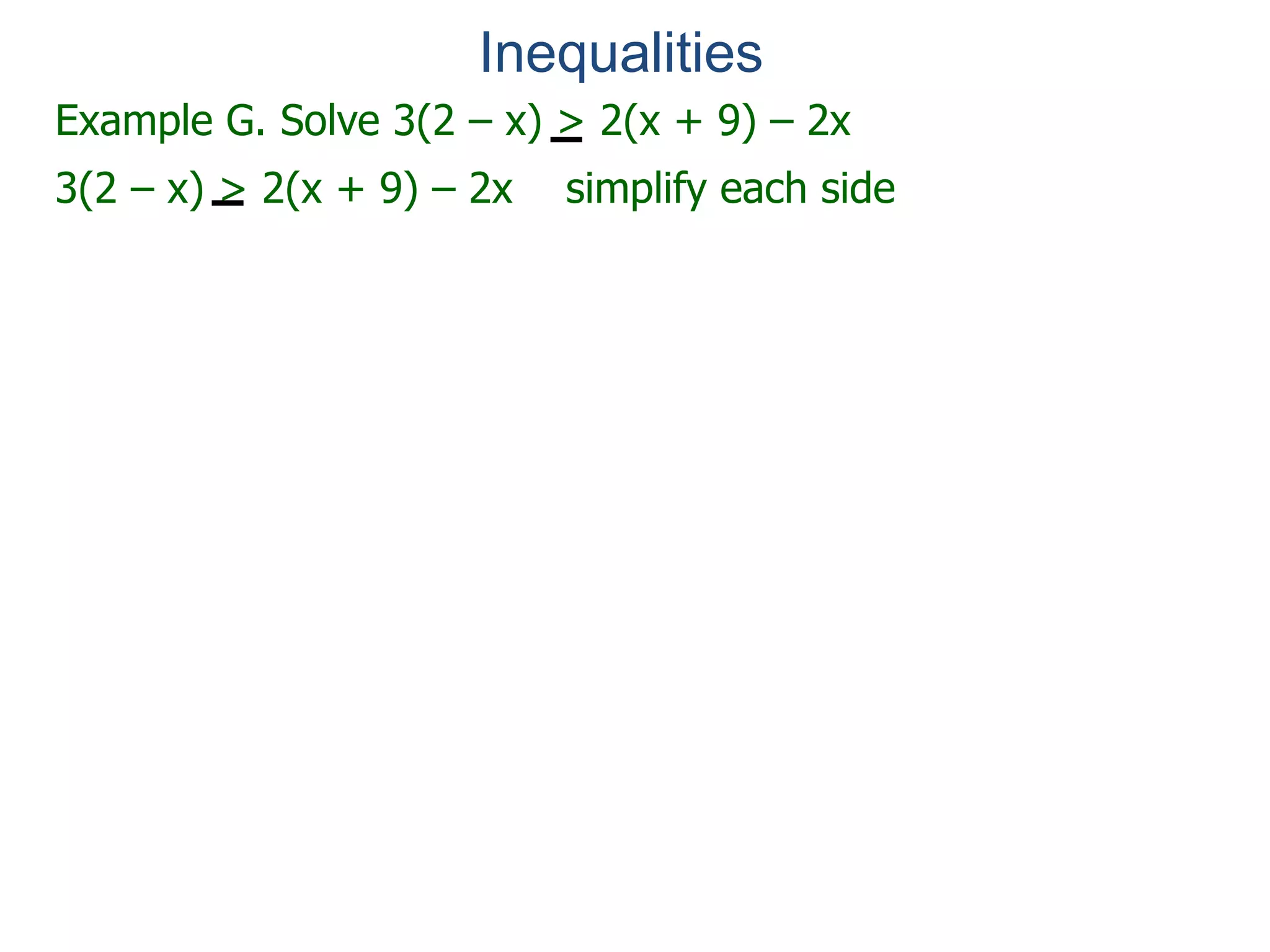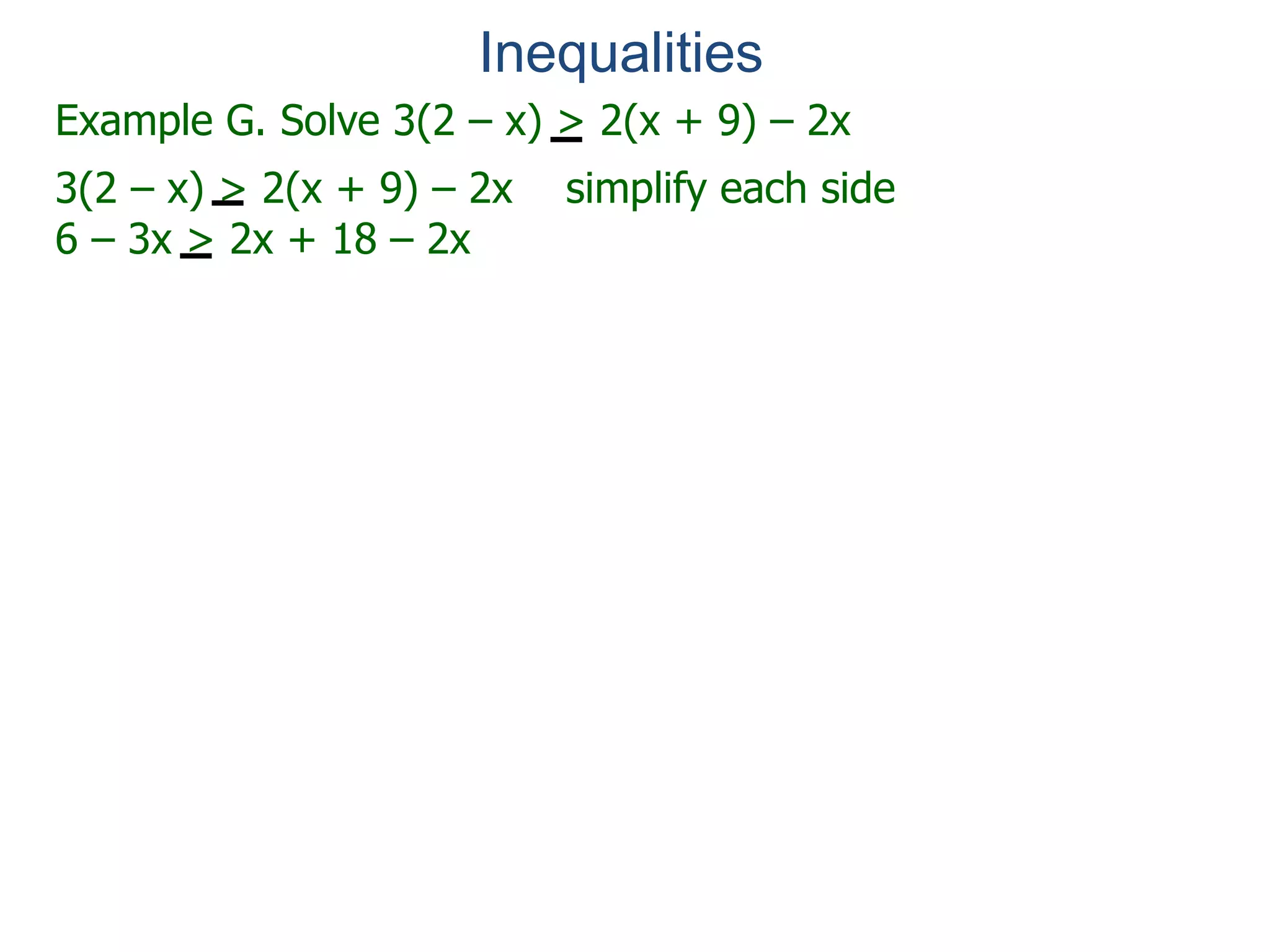The document discusses inequalities and the real number line. It explains that real numbers are associated with positions on a line, with positive numbers to the right of zero and negative numbers to the left. This line is called the real number line. Two numbers are related by an inequality if their corresponding positions on the real number line have one number being further to the right than the other. Inequalities can be used to represent intervals of numbers on the real number line.

1. Inequalities

2. We associate each real number with a position on a line,
positive numbers to the right and negative numbers to the left.
Inequalities

3. We associate each real number with a position on a line,
positive numbers to the right and negative numbers to the left.
-2 20 1 3
+
-1-3
–
Inequalities

4. We associate each real number with a position on a line,
positive numbers to the right and negative numbers to the left.
-2 20 1 3
+
-1-3
–
2/3
Inequalities

5. We associate each real number with a position on a line,
positive numbers to the right and negative numbers to the left.
-2 20 1 3
+
-1-3
–
2/3 2½
Inequalities

6. We associate each real number with a position on a line,
positive numbers to the right and negative numbers to the left.
-2 20 1 3
+
-1-3
–
2/3 2½ π  3.14..
Inequalities
–π  –3.14..

7. We associate each real number with a position on a line,
positive numbers to the right and negative numbers to the left.
-2 20 1 3
+
-1-3
–
2/3 2½ π  3.14..
This line with each position addressed by a real number is
called the real (number) line.
Inequalities
–π  –3.14..

8. We associate each real number with a position on a line,
positive numbers to the right and negative numbers to the left.
-2 20 1 3
+
-1-3
–
2/3 2½ π  3.14..
This line with each position addressed by a real number is
called the real (number) line.
Inequalities
–π  –3.14..
Given two numbers corresponding to two points on the real
line, we define the number to the right to be greater than the
number to the left.

9. We associate each real number with a position on a line,
positive numbers to the right and negative numbers to the left.
-2 20 1 3
+
-1-3
–
2/3 2½ π  3.14..
This line with each position addressed by a real number is
called the real (number) line.
Inequalities
+–
RL
–π  –3.14..
Given two numbers corresponding to two points on the real
line, we define the number to the right to be greater than the
number to the left.

10. We associate each real number with a position on a line,
positive numbers to the right and negative numbers to the left.
-2 20 1 3
+
-1-3
–
2/3 2½ π  3.14..
This line with each position addressed by a real number is
called the real (number) line.
Inequalities
+–
R
We write this as L < R and called this the natural form because
it corresponds to their respective positions on the real line.
L
<
–π  –3.14..
Given two numbers corresponding to two points on the real
line, we define the number to the right to be greater than the
number to the left.

11. We associate each real number with a position on a line,
positive numbers to the right and negative numbers to the left.
-2 20 1 3
+
-1-3
–
2/3 2½ π  3.14..
This line with each position addressed by a real number is
called the real (number) line.
Inequalities
+–
R
We write this as L < R and called this the natural form because
it corresponds to their respective positions on the real line.
This relation may also be written as R > L (less preferable).
L
<
–π  –3.14..
Given two numbers corresponding to two points on the real
line, we define the number to the right to be greater than the
number to the left.

12. Example A. 2 < 4, –3< –2, 0 > –1 are true statements
Inequalities

13. Example A. 2 < 4, –3< –2, 0 > –1 are true statements
and –2 < –5 , 5 < 3 are false statements.
Inequalities

14. Example A. 2 < 4, –3< –2, 0 > –1 are true statements
and –2 < –5 , 5 < 3 are false statements.
Inequalities
If we want all the numbers greater than 5, we may denote them
as "all number x where 5 < x".

15. Example A. 2 < 4, –3< –2, 0 > –1 are true statements
and –2 < –5 , 5 < 3 are false statements.
Inequalities
If we want all the numbers greater than 5, we may denote them
as "all number x where 5 < x". In general, we write "a < x" for all
the numbers x greater than a (excluding a).

16. Example A. 2 < 4, –3< –2, 0 > –1 are true statements
and –2 < –5 , 5 < 3 are false statements.
Inequalities
If we want all the numbers greater than 5, we may denote them
as "all number x where 5 < x". In general, we write "a < x" for all
the numbers x greater than a (excluding a). In picture,
+–
a
open dot
a < x

17. Example A. 2 < 4, –3< –2, 0 > –1 are true statements
and –2 < –5 , 5 < 3 are false statements.
Inequalities
If we want all the numbers greater than 5, we may denote them
as "all number x where 5 < x". In general, we write "a < x" for all
the numbers x greater than a (excluding a). In picture,
+–
a
open dot
If we want all the numbers x greater than or equal to a
(including a), we write it as a < x.
a < x

18. Example A. 2 < 4, –3< –2, 0 > –1 are true statements
and –2 < –5 , 5 < 3 are false statements.
Inequalities
If we want all the numbers greater than 5, we may denote them
as "all number x where 5 < x". In general, we write "a < x" for all
the numbers x greater than a (excluding a). In picture,
+–
a
open dot
If we want all the numbers x greater than or equal to a
(including a), we write it as a < x. In picture
+–
a
solid dot
a < x
a < x

19. Example A. 2 < 4, –3< –2, 0 > –1 are true statements
and –2 < –5 , 5 < 3 are false statements.
Inequalities
If we want all the numbers greater than 5, we may denote them
as "all number x where 5 < x". In general, we write "a < x" for all
the numbers x greater than a (excluding a). In picture,
+–
a
open dot
If we want all the numbers x greater than or equal to a
(including a), we write it as a < x. In picture
+–
a
solid dot
a < x
a < x
The numbers x fit the description a < x < b where a < b are all
the numbers x between a and b.

20. Example A. 2 < 4, –3< –2, 0 > –1 are true statements
and –2 < –5 , 5 < 3 are false statements.
Inequalities
If we want all the numbers greater than 5, we may denote them
as "all number x where 5 < x". In general, we write "a < x" for all
the numbers x greater than a (excluding a). In picture,
+–
a
open dot
If we want all the numbers x greater than or equal to a
(including a), we write it as a < x. In picture
+–
a
solid dot
a < x
a < x
The numbers x fit the description a < x < b where a < b are all
the numbers x between a and b.
+–
a a < x < b b

21. Example A. 2 < 4, –3< –2, 0 > –1 are true statements
and –2 < –5 , 5 < 3 are false statements.
Inequalities
If we want all the numbers greater than 5, we may denote them
as "all number x where 5 < x". In general, we write "a < x" for all
the numbers x greater than a (excluding a). In picture,
+–
a
open dot
If we want all the numbers x greater than or equal to a
(including a), we write it as a < x. In picture
+–
a
solid dot
a < x
a < x
The numbers x fit the description a < x < b where a < b are all
the numbers x between a and b. A line segment as such is
called an interval.
+–
a a < x < b b

22. Example B.
a. Draw –1 < x < 3.
Inequalities

23. Example B.
a. Draw –1 < x < 3.
Inequalities
It’s in the natural form.

24. Example B.
a. Draw –1 < x < 3.
Inequalities
It’s in the natural form. Mark the numbers and x on the line
in order accordingly.

25. Example B.
a. Draw –1 < x < 3.
0 3
+
-1
– x
Inequalities
It’s in the natural form. Mark the numbers and x on the line
in order accordingly.

26. Example B.
a. Draw –1 < x < 3.
0 3
+
-1
– x
b. Draw 0 > x > –3
Inequalities
It’s in the natural form. Mark the numbers and x on the line
in order accordingly.

27. Example B.
a. Draw –1 < x < 3.
0 3
+
-1
– x
b. Draw 0 > x > –3
Inequalities
It’s in the natural form. Mark the numbers and x on the line
in order accordingly.
Put it in the natural form –3 < x < 0.

28. Example B.
a. Draw –1 < x < 3.
0 3
+
-1
– x
b. Draw 0 > x > –3
Inequalities
It’s in the natural form. Mark the numbers and x on the line
in order accordingly.
Put it in the natural form –3 < x < 0.
Then mark the numbers and x in order accordingly.

29. Example B.
a. Draw –1 < x < 3.
0 3
+
-1
– x
b. Draw 0 > x > –3
0
+
-3
–
x
Inequalities
It’s in the natural form. Mark the numbers and x on the line
in order accordingly.
Put it in the natural form –3 < x < 0.
Then mark the numbers and x in order accordingly.

30. Example B.
a. Draw –1 < x < 3.
0 3
+
-1
– x
b. Draw 0 > x > –3
0
+
-3
–
x
Expressions such as 2 < x > 3 or 2 < x < –3 do not have
any solution.
Inequalities
It’s in the natural form. Mark the numbers and x on the line
in order accordingly.
Put it in the natural form –3 < x < 0.
Then mark the numbers and x in order accordingly.

31. Example B.
a. Draw –1 < x < 3.
0 3
+
-1
– x
b. Draw 0 > x > –3
0
+
-3
–
x
Expressions such as 2 < x > 3 or 2 < x < –3 do not have
any solution.
Inequalities
Adding or subtracting the same quantity to both retains the
inequality sign,
It’s in the natural form. Mark the numbers and x on the line
in order accordingly.
Put it in the natural form –3 < x < 0.
Then mark the numbers and x in order accordingly.

32. Example B.
a. Draw –1 < x < 3.
0 3
+
-1
– x
b. Draw 0 > x > –3
0
+
-3
–
x
Expressions such as 2 < x > 3 or 2 < x < –3 do not have
any solution.
Inequalities
Adding or subtracting the same quantity to both retains the
inequality sign, i.e. if a < b, then a ± c < b ± c.
It’s in the natural form. Mark the numbers and x on the line
in order accordingly.
Put it in the natural form –3 < x < 0.
Then mark the numbers and x in order accordingly.

33. Example B.
a. Draw –1 < x < 3.
0 3
+
-1
– x
b. Draw 0 > x > –3
0
+
-3
–
x
Expressions such as 2 < x > 3 or 2 < x < –3 do not have
any solution.
Inequalities
For example 6 < 12, then 6 + 3 < 12 + 3.
Adding or subtracting the same quantity to both retains the
inequality sign, i.e. if a < b, then a ± c < b ± c.
It’s in the natural form. Mark the numbers and x on the line
in order accordingly.
Put it in the natural form –3 < x < 0.
Then mark the numbers and x in order accordingly.

34. Example B.
a. Draw –1 < x < 3.
0 3
+
-1
– x
b. Draw 0 > x > –3
0
+
-3
–
x
Expressions such as 2 < x > 3 or 2 < x < –3 do not have
any solution.
Inequalities
For example 6 < 12, then 6 + 3 < 12 + 3.
We use the this fact to solve inequalities.
Adding or subtracting the same quantity to both retains the
inequality sign, i.e. if a < b, then a ± c < b ± c.
It’s in the natural form. Mark the numbers and x on the line
in order accordingly.
Put it in the natural form –3 < x < 0.
Then mark the numbers and x in order accordingly.

35. Example C. Solve x – 3 < 12 and draw the solution.
Inequalities

36. Example C. Solve x – 3 < 12 and draw the solution.
x – 3 < 12 add 3 to both sides
x – 3 + 3 < 12 + 3
Inequalities

37. Example C. Solve x – 3 < 12 and draw the solution.
x – 3 < 12 add 3 to both sides
x – 3 + 3 < 12 + 3
x < 15
Inequalities

38. Example C. Solve x – 3 < 12 and draw the solution.
x – 3 < 12 add 3 to both sides
x – 3 + 3 < 12 + 3
x < 15
0 15
+–
Inequalities
x

39. Example C. Solve x – 3 < 12 and draw the solution.
x – 3 < 12 add 3 to both sides
x – 3 + 3 < 12 + 3
x < 15
0 15
+–
Inequalities
x
A number c is positive means that 0 < c.

40. Example C. Solve x – 3 < 12 and draw the solution.
x – 3 < 12 add 3 to both sides
x – 3 + 3 < 12 + 3
x < 15
0 15
+–
Inequalities
x
A number c is positive means that 0 < c. We may multiply or
divide a positive number to the inequality and keep the same
inequality sign,

41. Example C. Solve x – 3 < 12 and draw the solution.
x – 3 < 12 add 3 to both sides
x – 3 + 3 < 12 + 3
x < 15
0 15
+–
Inequalities
x
A number c is positive means that 0 < c. We may multiply or
divide a positive number to the inequality and keep the same
inequality sign, i.e. if 0 < c and a < b

42. Example C. Solve x – 3 < 12 and draw the solution.
x – 3 < 12 add 3 to both sides
x – 3 + 3 < 12 + 3
x < 15
0 15
+–
Inequalities
x
A number c is positive means that 0 < c. We may multiply or
divide a positive number to the inequality and keep the same
inequality sign, i.e. if 0 < c and a < b, then ac < bc.

43. Example C. Solve x – 3 < 12 and draw the solution.
x – 3 < 12 add 3 to both sides
x – 3 + 3 < 12 + 3
x < 15
0 15
+–
Inequalities
x
A number c is positive means that 0 < c. We may multiply or
divide a positive number to the inequality and keep the same
inequality sign, i.e. if 0 < c and a < b, then ac < bc.
For example 6 < 12 is true,

44. Example C. Solve x – 3 < 12 and draw the solution.
x – 3 < 12 add 3 to both sides
x – 3 + 3 < 12 + 3
x < 15
0 15
+–
Inequalities
x
A number c is positive means that 0 < c. We may multiply or
divide a positive number to the inequality and keep the same
inequality sign, i.e. if 0 < c and a < b, then ac < bc.
For example 6 < 12 is true, then multiplying by 3
3*6 < 3*12

45. Example C. Solve x – 3 < 12 and draw the solution.
x – 3 < 12 add 3 to both sides
x – 3 + 3 < 12 + 3
x < 15
0 15
+–
Inequalities
x
A number c is positive means that 0 < c. We may multiply or
divide a positive number to the inequality and keep the same
inequality sign, i.e. if 0 < c and a < b, then ac < bc.
For example 6 < 12 is true, then multiplying by 3
3*6 < 3*12 or 18 < 36 is also true.

46. Example C. Solve x – 3 < 12 and draw the solution.
x – 3 < 12 add 3 to both sides
x – 3 + 3 < 12 + 3
x < 15
0 15
+–
Inequalities
x
A number c is positive means that 0 < c. We may multiply or
divide a positive number to the inequality and keep the same
inequality sign, i.e. if 0 < c and a < b, then ac < bc.
Example D. Solve 3x > 12 and draw the solution.
For example 6 < 12 is true, then multiplying by 3
3*6 < 3*12 or 18 < 36 is also true.

47. Example C. Solve x – 3 < 12 and draw the solution.
x – 3 < 12 add 3 to both sides
x – 3 + 3 < 12 + 3
x < 15
0 15
+–
Inequalities
x
A number c is positive means that 0 < c. We may multiply or
divide a positive number to the inequality and keep the same
inequality sign, i.e. if 0 < c and a < b, then ac < bc.
Example D. Solve 3x > 12 and draw the solution.
3x > 12
For example 6 < 12 is true, then multiplying by 3
3*6 < 3*12 or 18 < 36 is also true.

48. Example C. Solve x – 3 < 12 and draw the solution.
x – 3 < 12 add 3 to both sides
x – 3 + 3 < 12 + 3
x < 15
0 15
+–
Inequalities
x
A number c is positive means that 0 < c. We may multiply or
divide a positive number to the inequality and keep the same
inequality sign, i.e. if 0 < c and a < b, then ac < bc.
Example D. Solve 3x > 12 and draw the solution.
3x > 12 divide by 3 and keep the inequality sign
3x/3 > 12/3
For example 6 < 12 is true, then multiplying by 3
3*6 < 3*12 or 18 < 36 is also true.

49. Example C. Solve x – 3 < 12 and draw the solution.
x – 3 < 12 add 3 to both sides
x – 3 + 3 < 12 + 3
x < 15
0 15
+–
Inequalities
x
A number c is positive means that 0 < c. We may multiply or
divide a positive number to the inequality and keep the same
inequality sign, i.e. if 0 < c and a < b, then ac < bc.
Example D. Solve 3x > 12 and draw the solution.
3x > 12 divide by 3 and keep the inequality sign
3x/3 > 12/3
x > 4 or 4 < x
For example 6 < 12 is true, then multiplying by 3
3*6 < 3*12 or 18 < 36 is also true.

50. Example C. Solve x – 3 < 12 and draw the solution.
x – 3 < 12 add 3 to both sides
x – 3 + 3 < 12 + 3
x < 15
0 15
+–
Inequalities
x
A number c is positive means that 0 < c. We may multiply or
divide a positive number to the inequality and keep the same
inequality sign, i.e. if 0 < c and a < b, then ac < bc.
Example D. Solve 3x > 12 and draw the solution.
3x > 12 divide by 3 and keep the inequality sign
3x/3 > 12/3
x > 4 or 4 < x
40
+–
For example 6 < 12 is true, then multiplying by 3
3*6 < 3*12 or 18 < 36 is also true.
x

51. A number c is negative means c < 0.
Inequalities

52. A number c is negative means c < 0. Multiplying or dividing by
an negative number reverses the inequality sign,
Inequalities

53. A number c is negative means c < 0. Multiplying or dividing by
an negative number reverses the inequality sign,
i.e. if c < 0 and a < b then
Inequalities

54. A number c is negative means c < 0. Multiplying or dividing by
an negative number reverses the inequality sign,
i.e. if c < 0 and a < b then
ca > cb .
Inequalities

55. A number c is negative means c < 0. Multiplying or dividing by
an negative number reverses the inequality sign,
i.e. if c < 0 and a < b then
ca > cb .
Inequalities
For example 6 < 12 is true.

56. A number c is negative means c < 0. Multiplying or dividing by
an negative number reverses the inequality sign,
i.e. if c < 0 and a < b then
ca > cb .
Inequalities
For example 6 < 12 is true. If we multiply –1 to both sides then
(–1)6 > (–1)12
– 6 > –12 which is true.

57. A number c is negative means c < 0. Multiplying or dividing by
an negative number reverses the inequality sign,
i.e. if c < 0 and a < b then
ca > cb .
Inequalities
For example 6 < 12 is true. If we multiply –1 to both sides then
(–1)6 > (–1)12
– 6 > –12 which is true.
Multiplying by –1 switches the left-right positions of the originals.

58. A number c is negative means c < 0. Multiplying or dividing by
an negative number reverses the inequality sign,
i.e. if c < 0 and a < b then
ca > cb .
Inequalities
60
+–
12<
For example 6 < 12 is true. If we multiply –1 to both sides then
(–1)6 > (–1)12
– 6 > –12 which is true.
Multiplying by –1 switches the left-right positions of the originals.

59. A number c is negative means c < 0. Multiplying or dividing by
an negative number reverses the inequality sign,
i.e. if c < 0 and a < b then
ca > cb .
Inequalities
60
+–
12–6 <
For example 6 < 12 is true. If we multiply –1 to both sides then
(–1)6 > (–1)12
– 6 > –12 which is true.
Multiplying by –1 switches the left-right positions of the originals.

60. A number c is negative means c < 0. Multiplying or dividing by
an negative number reverses the inequality sign,
i.e. if c < 0 and a < b then
ca > cb .
Inequalities
60
+–
12–6–12 <<
For example 6 < 12 is true. If we multiply –1 to both sides then
(–1)6 > (–1)12
– 6 > –12 which is true.
Multiplying by –1 switches the left-right positions of the originals.

61. A number c is negative means c < 0. Multiplying or dividing by
an negative number reverses the inequality sign,
i.e. if c < 0 and a < b then
ca > cb .
Example E. Solve –x + 2 < 5 and draw the solution.
Inequalities
60
+–
12–6–12 <<
For example 6 < 12 is true. If we multiply –1 to both sides then
(–1)6 > (–1)12
– 6 > –12 which is true.
Multiplying by –1 switches the left-right positions of the originals.

62. A number c is negative means c < 0. Multiplying or dividing by
an negative number reverses the inequality sign,
i.e. if c < 0 and a < b then
ca > cb .
Example E. Solve –x + 2 < 5 and draw the solution.
–x + 2 < 5
Inequalities
60
+–
12–6–12 <<
For example 6 < 12 is true. If we multiply –1 to both sides then
(–1)6 > (–1)12
– 6 > –12 which is true.
Multiplying by –1 switches the left-right positions of the originals.

63. A number c is negative means c < 0. Multiplying or dividing by
an negative number reverses the inequality sign,
i.e. if c < 0 and a < b then
ca > cb .
Example E. Solve –x + 2 < 5 and draw the solution.
–x + 2 < 5 subtract 2 from both sides
–x < 3
Inequalities
60
+–
12–6–12 <<
For example 6 < 12 is true. If we multiply –1 to both sides then
(–1)6 > (–1)12
– 6 > –12 which is true.
Multiplying by –1 switches the left-right positions of the originals.

64. A number c is negative means c < 0. Multiplying or dividing by
an negative number reverses the inequality sign,
i.e. if c < 0 and a < b then
ca > cb .
Example E. Solve –x + 2 < 5 and draw the solution.
–x + 2 < 5 subtract 2 from both sides
–x < 3 multiply by –1 to get x, reverse the inequality
–(–x) > –3
x > –3
Inequalities
60
+–
12–6–12 <<
For example 6 < 12 is true. If we multiply –1 to both sides then
(–1)6 > (–1)12
– 6 > –12 which is true.
Multiplying by –1 switches the left-right positions of the originals.

65. A number c is negative means c < 0. Multiplying or dividing by
an negative number reverses the inequality sign,
i.e. if c < 0 and a < b then
ca > cb .
Example E. Solve –x + 2 < 5 and draw the solution.
–x + 2 < 5 subtract 2 from both sides
–x < 3 multiply by –1 to get x, reverse the inequality
–(–x) > –3
x > –3 or –3 < x
Inequalities
60
+–
12–6–12 <<
For example 6 < 12 is true. If we multiply –1 to both sides then
(–1)6 > (–1)12
– 6 > –12 which is true.
Multiplying by –1 switches the left-right positions of the originals.

66. A number c is negative means c < 0. Multiplying or dividing by
an negative number reverses the inequality sign,
i.e. if c < 0 and a < b then
ca > cb .
Example E. Solve –x + 2 < 5 and draw the solution.
–x + 2 < 5 subtract 2 from both sides
–x < 3 multiply by –1 to get x, reverse the inequality
–(–x) > –3
x > –3 or –3 < x
0
+
-3
–
Inequalities
60
+–
12–6–12 <<
For example 6 < 12 is true. If we multiply –1 to both sides then
(–1)6 > (–1)12
– 6 > –12 which is true.
Multiplying by –1 switches the left-right positions of the originals.

67. To solve inequalities:
1. Simplify both sides of the inequalities
Inequalities

68. To solve inequalities:
1. Simplify both sides of the inequalities
2. Gather the x-terms to one side and the number-terms to the
other sides
Inequalities

69. To solve inequalities:
1. Simplify both sides of the inequalities
2. Gather the x-terms to one side and the number-terms to the
other sides (use the “change side-change sign” rule).
Inequalities

70. To solve inequalities:
1. Simplify both sides of the inequalities
2. Gather the x-terms to one side and the number-terms to the
other sides (use the “change side-change sign” rule).
3. Multiply or divide to get x.
Inequalities

71. To solve inequalities:
1. Simplify both sides of the inequalities
2. Gather the x-terms to one side and the number-terms to the
other sides (use the “change side-change sign” rule).
3. Multiply or divide to get x. If we multiply or divide by
negative numbers to both sides, the inequality sign must be
turned around.
Inequalities

72. To solve inequalities:
1. Simplify both sides of the inequalities
2. Gather the x-terms to one side and the number-terms to the
other sides (use the “change side-change sign” rule).
3. Multiply or divide to get x. If we multiply or divide by
negative numbers to both sides, the inequality sign must be
turned around. This rule can be avoided by keeping the
x-term positive.
Inequalities

73. To solve inequalities:
1. Simplify both sides of the inequalities
2. Gather the x-terms to one side and the number-terms to the
other sides (use the “change side-change sign” rule).
3. Multiply or divide to get x. If we multiply or divide by
negative numbers to both sides, the inequality sign must be
turned around. This rule can be avoided by keeping the
x-term positive.
Inequalities
Example F. Solve 3x + 5 > x + 9

74. To solve inequalities:
1. Simplify both sides of the inequalities
2. Gather the x-terms to one side and the number-terms to the
other sides (use the “change side-change sign” rule).
3. Multiply or divide to get x. If we multiply or divide by
negative numbers to both sides, the inequality sign must be
turned around. This rule can be avoided by keeping the
x-term positive.
Inequalities
Example F. Solve 3x + 5 > x + 9
3x + 5 > x + 9 move the x and 5, change side-change sign

75. To solve inequalities:
1. Simplify both sides of the inequalities
2. Gather the x-terms to one side and the number-terms to the
other sides (use the “change side-change sign” rule).
3. Multiply or divide to get x. If we multiply or divide by
negative numbers to both sides, the inequality sign must be
turned around. This rule can be avoided by keeping the
x-term positive.
Inequalities
Example F. Solve 3x + 5 > x + 9
3x + 5 > x + 9 move the x and 5, change side-change sign
3x – x > 9 – 5

76. To solve inequalities:
1. Simplify both sides of the inequalities
2. Gather the x-terms to one side and the number-terms to the
other sides (use the “change side-change sign” rule).
3. Multiply or divide to get x. If we multiply or divide by
negative numbers to both sides, the inequality sign must be
turned around. This rule can be avoided by keeping the
x-term positive.
Inequalities
Example F. Solve 3x + 5 > x + 9
3x + 5 > x + 9 move the x and 5, change side-change sign
3x – x > 9 – 5
2x > 4

77. To solve inequalities:
1. Simplify both sides of the inequalities
2. Gather the x-terms to one side and the number-terms to the
other sides (use the “change side-change sign” rule).
3. Multiply or divide to get x. If we multiply or divide by
negative numbers to both sides, the inequality sign must be
turned around. This rule can be avoided by keeping the
x-term positive.
Inequalities
Example F. Solve 3x + 5 > x + 9
3x + 5 > x + 9 move the x and 5, change side-change sign
3x – x > 9 – 5
2x > 4 div. 2
2x
2
4
2>

78. To solve inequalities:
1. Simplify both sides of the inequalities
2. Gather the x-terms to one side and the number-terms to the
other sides (use the “change side-change sign” rule).
3. Multiply or divide to get x. If we multiply or divide by
negative numbers to both sides, the inequality sign must be
turned around. This rule can be avoided by keeping the
x-term positive.
Inequalities
Example F. Solve 3x + 5 > x + 9
3x + 5 > x + 9 move the x and 5, change side-change sign
3x – x > 9 – 5
2x > 4 div. 2
2x
2
4
2>
x > 2 or 2 < x

79. To solve inequalities:
1. Simplify both sides of the inequalities
2. Gather the x-terms to one side and the number-terms to the
other sides (use the “change side-change sign” rule).
3. Multiply or divide to get x. If we multiply or divide by
negative numbers to both sides, the inequality sign must be
turned around. This rule can be avoided by keeping the
x-term positive.
Inequalities
Example F. Solve 3x + 5 > x + 9
3x + 5 > x + 9 move the x and 5, change side-change sign
3x – x > 9 – 5
2x > 4 div. 2
20
+–
2x
2
4
2>
x > 2 or 2 < x

80. Example G. Solve 3(2 – x) > 2(x + 9) – 2x
Inequalities

81. Example G. Solve 3(2 – x) > 2(x + 9) – 2x
3(2 – x) > 2(x + 9) – 2x simplify each side
Inequalities

82. Example G. Solve 3(2 – x) > 2(x + 9) – 2x
3(2 – x) > 2(x + 9) – 2x simplify each side
6 – 3x > 2x + 18 – 2x
Inequalities

83. Example G. Solve 3(2 – x) > 2(x + 9) – 2x
3(2 – x) > 2(x + 9) – 2x simplify each side
6 – 3x > 2x + 18 – 2x
6 – 3x > 18
Inequalities

84. Example G. Solve 3(2 – x) > 2(x + 9) – 2x
3(2 – x) > 2(x + 9) – 2x simplify each side
6 – 3x > 2x + 18 – 2x
6 – 3x > 18 move 18 and –3x (change sign)
6 – 18 > 3x
Inequalities

85. Example G. Solve 3(2 – x) > 2(x + 9) – 2x
3(2 – x) > 2(x + 9) – 2x simplify each side
6 – 3x > 2x + 18 – 2x
6 – 3x > 18 move 18 and –3x (change sign)
6 – 18 > 3x
– 12 > 3x
Inequalities

86. Example G. Solve 3(2 – x) > 2(x + 9) – 2x
3(2 – x) > 2(x + 9) – 2x simplify each side
6 – 3x > 2x + 18 – 2x
6 – 3x > 18 move 18 and –3x (change sign)
6 – 18 > 3x
– 12 > 3x
–12
3
3x
3
>
div. by 3 (no need to switch >)
Inequalities

87. Example G. Solve 3(2 – x) > 2(x + 9) – 2x
3(2 – x) > 2(x + 9) – 2x simplify each side
6 – 3x > 2x + 18 – 2x
6 – 3x > 18 move 18 and –3x (change sign)
6 – 18 > 3x
– 12 > 3x
–12
3
3x
3
>
–4 > x or x < –4
div. by 3 (no need to switch >)
Inequalities

88. Example G. Solve 3(2 – x) > 2(x + 9) – 2x
3(2 – x) > 2(x + 9) – 2x simplify each side
6 – 3x > 2x + 18 – 2x
6 – 3x > 18 move 18 and –3x (change sign)
6 – 18 > 3x
– 12 > 3x
0
+
–12
3
3x
3
>
-4
div. by 3 (no need to switch >)
Inequalities
–4 > x or x < –4

89. Example G. Solve 3(2 – x) > 2(x + 9) – 2x
3(2 – x) > 2(x + 9) – 2x simplify each side
6 – 3x > 2x + 18 – 2x
6 – 3x > 18 move 18 and –3x (change sign)
6 – 18 > 3x
– 12 > 3x
0
+
–12
3
3x
3
>
-4
div. by 3 (no need to switch >)
Inequalities
We also have inequalities in the form of intervals.
–4 > x or x < –4

90. Example G. Solve 3(2 – x) > 2(x + 9) – 2x
3(2 – x) > 2(x + 9) – 2x simplify each side
6 – 3x > 2x + 18 – 2x
6 – 3x > 18 move 18 and –3x (change sign)
6 – 18 > 3x
– 12 > 3x
0
+
–12
3
3x
3
>
-4
div. by 3 (no need to switch >)
Inequalities
We also have inequalities in the form of intervals. We solve
them by +, –, * , / to all three parts of the inequalities.
–4 > x or x < –4

91. Example G. Solve 3(2 – x) > 2(x + 9) – 2x
3(2 – x) > 2(x + 9) – 2x simplify each side
6 – 3x > 2x + 18 – 2x
6 – 3x > 18 move 18 and –3x (change sign)
6 – 18 > 3x
– 12 > 3x
0
+
–12
3
3x
3
>
-4
div. by 3 (no need to switch >)
Inequalities
We also have inequalities in the form of intervals. We solve
them by +, –, * , / to all three parts of the inequalities.
Again, we + or – remove the number term in the middle first,
–4 > x or x < –4

92. Example G. Solve 3(2 – x) > 2(x + 9) – 2x
3(2 – x) > 2(x + 9) – 2x simplify each side
6 – 3x > 2x + 18 – 2x
6 – 3x > 18 move 18 and –3x (change sign)
6 – 18 > 3x
– 12 > 3x
0
+
–12
3
3x
3
>
-4
div. by 3 (no need to switch >)
Inequalities
We also have inequalities in the form of intervals. We solve
them by +, –, * , / to all three parts of the inequalities.
Again, we + or – remove the number term in the middle first,
then divide or multiply to get x.
–4 > x or x < –4

93. Example G. Solve 3(2 – x) > 2(x + 9) – 2x
3(2 – x) > 2(x + 9) – 2x simplify each side
6 – 3x > 2x + 18 – 2x
6 – 3x > 18 move 18 and –3x (change sign)
6 – 18 > 3x
– 12 > 3x
0
+
–12
3
3x
3
>
-4
div. by 3 (no need to switch >)
Inequalities
We also have inequalities in the form of intervals. We solve
them by +, –, * , / to all three parts of the inequalities.
Again, we + or – remove the number term in the middle first,
then divide or multiply to get x. The answer is an interval of
numbers.
–4 > x or x < –4

94. Example H. (Interval Inequality)
Solve 12 > –2x + 6 > –4 and draw
Inequalities

95. Example H. (Interval Inequality)
Solve 12 > –2x + 6 > –4 and draw.
12 > –2x + 6 > –4 subtract 6
–6 –6 –6
Inequalities

96. Example H. (Interval Inequality)
Solve 12 > –2x + 6 > –4 and draw.
12 > –2x + 6 > –4 subtract 6
–6 –6 –6
6 > –2x > –10
Inequalities

97. Example H. (Interval Inequality)
Solve 12 > –2x + 6 > –4 and draw.
12 > –2x + 6 > –4 subtract 6
–6 –6 –6
6 > –2x > –10 div. by -2, switch inequality sign
6
-2
-2x
-2<
-10
-2
<
Inequalities

98. Example H. (Interval Inequality)
Solve 12 > –2x + 6 > –4 and draw.
12 > –2x + 6 > –4 subtract 6
–6 –6 –6
6 > –2x > –10
-3 < x < 5
div. by -2, switch inequality sign
6
-2
-2x
-2<
-10
-2
<
Inequalities

99. Example H. (Interval Inequality)
Solve 12 > –2x + 6 > –4 and draw.
12 > –2x + 6 > –4 subtract 6
–6 –6 –6
6 > –2x > –10
0
+
-3 < x < 5
5
div. by -2, switch inequality sign
6
-2
-2x
-2<
-10
-2
<
-3
Inequalities
The following adjectives or comparison phrases may be
translated into inequalities:

100. The following adjectives or comparison phrases may be
translated into inequalities:
“positive”↔“negative”,
“non–positive”↔”non–negative”,
“more/greater than”↔ “less/smaller than”,
“no more/greater than”↔ “no less/smaller than”,
“ at least” ↔”at most”,
Inequalities and Comparative Phrases

101. The following adjectives or comparison phrases may be
translated into inequalities:
“positive”↔“negative”,
“non–positive”↔”non–negative”,
“more/greater than”↔ “less/smaller than”,
“no more/greater than”↔ “no less/smaller than”,
“ at least” ↔”at most”,
Positive vs. Negative”
Inequalities and Comparative Phrases

102. The following adjectives or comparison phrases may be
translated into inequalities:
“positive”↔“negative”,
“non–positive”↔”non–negative”,
“more/greater than”↔ “less/smaller than”,
“no more/greater than”↔ “no less/smaller than”,
“ at least” ↔”at most”,
A quantity x is positive means that x is more than 0, i.e. 0 < x,
Positive vs. Negative”
Inequalities and Comparative Phrases

103. The following adjectives or comparison phrases may be
translated into inequalities:
“positive”↔“negative”,
“non–positive”↔”non–negative”,
“more/greater than”↔ “less/smaller than”,
“no more/greater than”↔ “no less/smaller than”,
“ at least” ↔”at most”,
A quantity x is positive means that x is more than 0, i.e. 0 < x,
0
+x is positive
Positive vs. Negative”
On the real line:
Inequalities and Comparative Phrases

104. The following adjectives or comparison phrases may be
translated into inequalities:
“positive”↔“negative”,
“non–positive”↔”non–negative”,
“more/greater than”↔ “less/smaller than”,
“no more/greater than”↔ “no less/smaller than”,
“ at least” ↔”at most”,
A quantity x is positive means that x is more than 0, i.e. 0 < x,
and that x is negative means that x is less than 0, i.e. x < 0.
0
+– x is negative x is positive
Positive vs. Negative”
On the real line:
Inequalities and Comparative Phrases

105. The following adjectives or comparison phrases may be
translated into inequalities:
“positive”↔“negative”,
“non–positive”↔”non–negative”,
“more/greater than”↔ “less/smaller than”,
“no more/greater than”↔ “no less/smaller than”,
“ at least” ↔”at most”,
A quantity x is positive means that x is more than 0, i.e. 0 < x,
and that x is negative means that x is less than 0, i.e. x < 0.
0
+– x is negative x is positive
Hence “the temperature T is positive” is translated as “0 < T”.
“the account balance A is negative”, is translated as “A < 0”.
Positive vs. Negative”
On the real line:
Inequalities and Comparative Phrases

106. The following adjectives or comparison phrases may be
translated into inequalities:
“positive”↔“negative”,
“non–positive”↔”non–negative”,
“more/greater than”↔ “less/smaller than”,
“no more/greater than”↔ “no less/smaller than”,
“ at least” ↔”at most”,
A quantity x is positive means that x is more than 0, i.e. 0 < x,
and that x is negative means that x is less than 0, i.e. x < 0.
0
+– x is negative x is positive
Hence “the temperature T is positive” is translated as “0 < T”.
“the account balance A is negative”, is translated as “A < 0”.
Positive vs. Negative”
On the real line:
Inequalities and Comparative Phrases

107. Inequalities and Comparative Phrases
Non–Positive vs. Non–Negative

108. A quantity x is non–positive means x is not positive, or “x ≤ 0”,
and that x is non–negative means x is not negative, or “0 ≤ x”,
Non–Positive vs. Non–Negative
Inequalities and Comparative Phrases

109. A quantity x is non–positive means x is not positive, or “x ≤ 0”,
and that x is non–negative means x is not negative, or “0 ≤ x”,
0
+
– x is non–positive
x is non–negative
Non–Positive vs. Non–Negative
On the real line:
Inequalities and Comparative Phrases

110. A quantity x is non–positive means x is not positive, or “x ≤ 0”,
and that x is non–negative means x is not negative, or “0 ≤ x”,
0
+
– x is non–positive
x is non–negative
Hence “the temperature T is non–positive” is “T ≤ 0”.
“the account balance A is non–negative” is “0 ≤ A”.
Non–Positive vs. Non–Negative
On the real line:
Inequalities and Comparative Phrases

111. A quantity x is non–positive means x is not positive, or “x ≤ 0”,
and that x is non–negative means x is not negative, or “0 ≤ x”,
0
+
– x is non–positive
x is non–negative
Hence “the temperature T is non–positive” is “T ≤ 0”.
“the account balance A is non–negative” is “0 ≤ A”.
Non–Positive vs. Non–Negative
On the real line:
“More/greater than” vs “Less/smaller than”
Inequalities and Comparative Phrases

112. A quantity x is non–positive means x is not positive, or “x ≤ 0”,
and that x is non–negative means x is not negative, or “0 ≤ x”,
0
+
– x is non–positive
x is non–negative
Hence “the temperature T is non–positive” is “T ≤ 0”.
“the account balance A is non–negative” is “0 ≤ A”.
Non–Positive vs. Non–Negative
On the real line:
“More/greater than” vs “Less/smaller than”
Let C be a number, x is greater than C means “C < x”,
and that x is less than C means “x < C”.
Inequalities and Comparative Phrases

113. A quantity x is non–positive means x is not positive, or “x ≤ 0”,
and that x is non–negative means x is not negative, or “0 ≤ x”,
0
+
– x is non–positive
x is non–negative
Hence “the temperature T is non–positive” is “T ≤ 0”.
“the account balance A is non–negative” is “0 ≤ A”.
Non–Positive vs. Non–Negative
On the real line:
“More/greater than” vs “Less/smaller than”
Let C be a number, x is greater than C means “C < x”,
and that x is less than C means “x < C”.
C
x is less than C
x is more than COn the real line:
Inequalities and Comparative Phrases

114. A quantity x is non–positive means x is not positive, or “x ≤ 0”,
and that x is non–negative means x is not negative, or “0 ≤ x”,
0
+
– x is non–positive
x is non–negative
Hence “the temperature T is non–positive” is “T ≤ 0”.
“the account balance A is non–negative” is “0 ≤ A”.
Non–Positive vs. Non–Negative
On the real line:
“More/greater than” vs “Less/smaller than”
Let C be a number, x is greater than C means “C < x”,
and that x is less than C means “x < C”.
C
x is less than C
x is more than C
Hence “the temperature T is more than –5 ” is “–5 < T”.
“the account balance A is less than 1,000” is “A < 1,000”.
On the real line:
Inequalities and Comparative Phrases

115. “ No more/greater than” vs “No less/smaller than”
Inequalities and Comparative Phrases

116. “ No more/greater than” vs “No less/smaller than”
A quantity x is no more greater than C means “x ≤ C”,
and that x is no–less than C means “C ≤ x”,
Inequalities and Comparative Phrases

117. “ No more/greater than” vs “No less/smaller than”
A quantity x is no more greater than C means “x ≤ C”,
and that x is no–less than C means “C ≤ x”,
0
+
– x is no more than C
x is no less than COn the real line:
C
Inequalities and Comparative Phrases

118. “ No more/greater than” vs “No less/smaller than”
A quantity x is no more greater than C means “x ≤ C”,
and that x is no–less than C means “C ≤ x”,
0
+
– x is no more than C
x is no less than C
“The temperature T is no–more than 250o” is “T ≤ 250”.
“The account balance A is no–less than 500” is “500 ≤ A”.
On the real line:
C
Inequalities and Comparative Phrases

119. “ No more/greater than” vs “No less/smaller than”
A quantity x is no more greater than C means “x ≤ C”,
and that x is no–less than C means “C ≤ x”,
0
+
– x is no more than C
x is no less than C
“The temperature T is no–more than 250o” is “T ≤ 250”.
“The account balance A is no–less than 500” is “500 ≤ A”.
On the real line:
C
“At least” vs “At most”
“At least C” is the same as “no less than C” and
“at most C” means “no more than C”.
Inequalities and Comparative Phrases

120. “ No more/greater than” vs “No less/smaller than”
A quantity x is no more greater than C means “x ≤ C”,
and that x is no–less than C means “C ≤ x”,
0
+
– x is no more than C
x is no less than C
“The temperature T is no–more than 250o” is “T ≤ 250”.
“The account balance A is no–less than 500” is “500 ≤ A”.
On the real line:
C
“At least” vs “At most”
“At least C” is the same as “no less than C” and
“at most C” means “no more than C”.
0
+
– x is at most C
x is at least COn the real line:
C
Inequalities and Comparative Phrases

121. “ No more/greater than” vs “No less/smaller than”
A quantity x is no more greater than C means “x ≤ C”,
and that x is no–less than C means “C ≤ x”,
0
+
– x is no more than C
x is no less than C
“The temperature T is no–more than 250o” is “T ≤ 250”.
“The account balance A is no–less than 500” is “500 ≤ A”.
On the real line:
C
“At least” vs “At most”
“At least C” is the same as “no less than C” and
“at most C” means “no more than C”.
0
+
– x is at most C
x is at least C
“The temperature T is at least 250o” is “250o ≤ T”.
“The account balance A is at most than 500” is “A ≤ 500”.
On the real line:
C
Inequalities and Comparative Phrases

122. Inequalities
Exercise. A. Draw the following Inequalities. Indicate clearly
whether the end points are included or not.
1. x < 3 2. –5 ≤ x 3. x < –8 4. x ≤ 12
B. Write in the natural form then draw them.
5. x ≥ 3 6. –5 > x 7. x ≥ –8 8. x > 12
C. Draw the following intervals, state so if it is impossible.
9. 6 > x ≥ 3 10. –5 < x ≤ 2 11. 1 > x ≥ –8 12. 4 < x ≤ 2
13. 6 > x ≥ 8 14. –5 > x ≤ 2 15. –7 ≤ x ≤ –3 16. –7 ≤ x ≤ –9
D. Solve the following Inequalities and draw the solution.
17. x + 5 < 3 18. –5 ≤ 2x + 3 19. 3x + 1 < –8
20. 2x + 3 ≤ 12 – x 21. –3x + 5 ≥ 1 – 4x
22. 2(x + 2) ≥ 5 – (x – 1) 23. 3(x – 1) + 2 ≤ – 2x – 9
24. –2(x – 3) > 2(–x – 1) + 3x 25. –(x + 4) – 2 ≤ 4(x – 1)
26. x + 2(x – 3) < 2(x – 1) – 2
27. –2(x – 3) + 3 ≥ 2(x – 1) + 3x + 13

123. Inequalities
F. Solve the following interval inequalities.
28. –4 ≤
2
x 29. 7 >
3
–x 30. < –4–x
E. Clear the denominator first then solve and draw the solution.
5
x2 3
1 2
3
2
+ ≥ x31. x4
–3
3
–4
– 1> x32.
x
2 8
3 3
4
5– ≤33. x
8 12
–5 7
1+ >34.
x
2 3
–3 2
3
4
4
1–+ x35. x4 6
5 5
3
–1
– 2+ < x36.
x
12 2
7 3
6
1
4
3–– ≥ x37.
≤
40. – 2 < x + 2 < 5 41. –1 ≥ 2x – 3 ≥ –11
42. –5 ≤ 1 – 3x < 10 43. 11 > –1 – 3x > –7
38. –6 ≤ 3x < 12 39. 8 > –2x > –4

124. Exercise. G. Draw the following Inequalities. Translate each
inequality into an English phrase. (There might be more than
one ways to do it)
1. x < 3 2. –5 ≤ x 3. x < –8 4. x ≤ 12
5. x ≥ 3 6. –5 > x 7. x ≥ –8 8. x > 12
Exercise. B. Translate each English phrase into an inequality.
Draw the Inequalities.
Let P be the number of people on a bus.
9. There were at least 50 people on the bus.
10. There were no more than 50 people on the bus.
11. There were less than 30 people on the bus.
12. There were no less than 28 people on the bus.
Let T be temperature outside.
13. The temperature is no more than –2o.
14. The temperature is at least than 35o.
15. The temperature is positive.
Inequalities and Comparative Phrases

125. Let M be the amount of money I have.
16. I have at most $25.
17. I have non–positive amount of money.
18. I have less than $45.
19. I have at least $250.
Let the basement floor number be given as negative number
and that F be floor number that we are on.
20. We are below the 7th floor.
21. We are above the first floor.
22. We are not below the 3rd floor basement.
24. We are on at least the 45th floor.
25. We are between the 4th floor basement and the 10th
floor.
26. We are in the basement.
Inequalities and Comparative Phrases