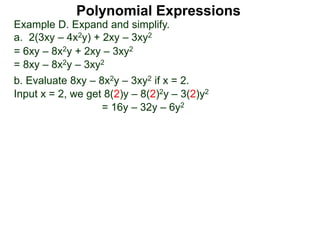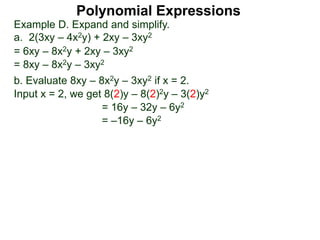The document discusses polynomial expressions in mathematics. It defines a polynomial as the sum of monomial terms, where a monomial is a number multiplied by a variable raised to a non-negative integer power. The degree of a polynomial is defined as the highest exponent among its monomial terms. Several examples of evaluating monomials and polynomials are provided by substituting specific values for variables.

1. Polynomial Expressions

2. A mathematics expression is a calculation procedure which
is written using numbers, variables, and operation-symbols.
Polynomial Expressions

3. A mathematics expression is a calculation procedure which
is written using numbers, variables, and operation-symbols.
The purposes of this symbolic-form are clarity and simplicity.
Polynomial Expressions

4. For example, let x represent a number,
then “2 + 3x” means to “sum 2 and 3 times x”,
A mathematics expression is a calculation procedure which
is written using numbers, variables, and operation-symbols.
The purposes of this symbolic-form are clarity and simplicity.
Polynomial Expressions

5. For example, let x represent a number,
then “2 + 3x” means to “sum 2 and 3 times x”,
A mathematics expression is a calculation procedure which
is written using numbers, variables, and operation-symbols.
The purposes of this symbolic-form are clarity and simplicity.
Polynomial Expressions
The English phrase
“sum 2 and 3 times x”
is ambiguous.

6. For example, let x represent a number,
then “2 + 3x” means to “sum 2 and 3 times x”,
“4x2 – 5x” means to
“subtract 5 times x from 4 times the square of x”,
A mathematics expression is a calculation procedure which
is written using numbers, variables, and operation-symbols.
The purposes of this symbolic-form are clarity and simplicity.
Polynomial Expressions
The English phrase
“sum 2 and 3 times x”
is ambiguous.

7. For example, let x represent a number,
then “2 + 3x” means to “sum 2 and 3 times x”,
“4x2 – 5x” means to
“subtract 5 times x from 4 times the square of x”,
(3 – 2x)2 means to
“square of the difference of 3 and twice x”.
A mathematics expression is a calculation procedure which
is written using numbers, variables, and operation-symbols.
The purposes of this symbolic-form are clarity and simplicity.
Polynomial Expressions
The English phrase
“sum 2 and 3 times x”
is ambiguous.

8. For example, let x represent a number,
then “2 + 3x” means to “sum 2 and 3 times x”,
“4x2 – 5x” means to
“subtract 5 times x from 4 times the square of x”,
(3 – 2x)2 means to
“square of the difference of 3 and twice x”.
A mathematics expression is a calculation procedure which
is written using numbers, variables, and operation-symbols.
The purposes of this symbolic-form are clarity and simplicity.
Polynomial Expressions
The English phrase
“sum 2 and 3 times x”
is ambiguous.
These are complicated!

9. For example, let x represent a number,
then “2 + 3x” means to “sum 2 and 3 times x”,
“4x2 – 5x” means to
“subtract 5 times x from 4 times the square of x”,
(3 – 2x)2 means to
“square of the difference of 3 and twice x”.
A mathematics expression is a calculation procedure which
is written using numbers, variables, and operation-symbols.
The purposes of this symbolic-form are clarity and simplicity.
The simplest form of expression are #xN, where N is a non-
negative integer and # is a number, is called a monomial
(one-term).
Polynomial Expressions
The English phrase
“sum 2 and 3 times x”
is ambiguous.
These are complicated!

10. For example, let x represent a number,
then “2 + 3x” means to “sum 2 and 3 times x”,
“4x2 – 5x” means to
“subtract 5 times x from 4 times the square of x”,
(3 – 2x)2 means to
“square of the difference of 3 and twice x”.
A mathematics expression is a calculation procedure which
is written using numbers, variables, and operation-symbols.
The purposes of this symbolic-form are clarity and simplicity.
The simplest form of expression are #xN, where N is a non-
negative integer and # is a number, is called a monomial
(one-term). For example –1, 2x, 3x2, and –4x3 are monomials.
Polynomial Expressions
The English phrase
“sum 2 and 3 times x”
is ambiguous.
These are complicated!

11. For example, let x represent a number,
then “2 + 3x” means to “sum 2 and 3 times x”,
“4x2 – 5x” means to
“subtract 5 times x from 4 times the square of x”,
(3 – 2x)2 means to
“square of the difference of 3 and twice x”.
A mathematics expression is a calculation procedure which
is written using numbers, variables, and operation-symbols.
The purposes of this symbolic-form are clarity and simplicity.
The simplest form of expression are #xN, where N is a non-
negative integer and # is a number, is called a monomial
(one-term). For example –1, 2x, 3x2, and –4x3 are monomials.
If N = 0 we’ve the constants, N = 1, the linear monomials #x.
Polynomial Expressions
The English phrase
“sum 2 and 3 times x”
is ambiguous.
These are complicated!

12. For example, let x represent a number,
then “2 + 3x” means to “sum 2 and 3 times x”,
“4x2 – 5x” means to
“subtract 5 times x from 4 times the square of x”,
(3 – 2x)2 means to
“square of the difference of 3 and twice x”.
A mathematics expression is a calculation procedure which
is written using numbers, variables, and operation-symbols.
The purposes of this symbolic-form are clarity and simplicity.
Example A. Evaluate the monomials if y = –4
a. 3y2
The simplest form of expression are #xN, where N is a non-
negative integer and # is a number, is called a monomial
(one-term). For example –1, 2x, 3x2, and –4x3 are monomials.
If N = 0 we’ve the constants, N = 1, the linear monomials #x.
Polynomial Expressions
The English phrase
“sum 2 and 3 times x”
is ambiguous.
These are complicated!

13. For example, let x represent a number,
then “2 + 3x” means to “sum 2 and 3 times x”,
“4x2 – 5x” means to
“subtract 5 times x from 4 times the square of x”,
(3 – 2x)2 means to
“square of the difference of 3 and twice x”.
A mathematics expression is a calculation procedure which
is written using numbers, variables, and operation-symbols.
The purposes of this symbolic-form are clarity and simplicity.
Example A. Evaluate the monomials if y = –4
a. 3y2
3y2  3(–4)2
The simplest form of expression are #xN, where N is a non-
negative integer and # is a number, is called a monomial
(one-term). For example –1, 2x, 3x2, and –4x3 are monomials.
If N = 0 we’ve the constants, N = 1, the linear monomials #x.
Polynomial Expressions
The English phrase
“sum 2 and 3 times x”
is ambiguous.
These are complicated!

14. For example, let x represent a number,
then “2 + 3x” means to “sum 2 and 3 times x”,
“4x2 – 5x” means to
“subtract 5 times x from 4 times the square of x”,
(3 – 2x)2 means to
“square of the difference of 3 and twice x”.
A mathematics expression is a calculation procedure which
is written using numbers, variables, and operation-symbols.
The purposes of this symbolic-form are clarity and simplicity.
Example A. Evaluate the monomials if y = –4
a. 3y2
3y2  3(–4)2 = 3(16) = 48
The simplest form of expression are #xN, where N is a non-
negative integer and # is a number, is called a monomial
(one-term). For example –1, 2x, 3x2, and –4x3 are monomials.
If N = 0 we’ve the constants, N = 1, the linear monomials #x.
Polynomial Expressions
The English phrase
“sum 2 and 3 times x”
is ambiguous.
These are complicated!

15. b. –3y2 (y = –4)
Polynomial Expressions

16. b. –3y2 (y = –4)
–3y2  –3(–4)2
Polynomial Expressions

17. b. –3y2 (y = –4)
–3y2  –3(–4)2
= –3(16) = –48.
Polynomial Expressions

18. b. –3y2 (y = –4)
–3y2  –3(–4)2
= –3(16) = –48.
c. –3y3
Polynomial Expressions

19. b. –3y2 (y = –4)
–3y2  –3(–4)2
= –3(16) = –48.
c. –3y3
–3y3  – 3(–4)3
Polynomial Expressions

20. b. –3y2 (y = –4)
–3y2  –3(–4)2
= –3(16) = –48.
c. –3y3
–3y3  – 3(–4)3
= – 3(–64)
Polynomial Expressions

21. b. –3y2 (y = –4)
–3y2  –3(–4)2
= –3(16) = –48.
c. –3y3
–3y3  – 3(–4)3
= – 3(–64) = 192
Polynomial Expressions

22. b. –3y2 (y = –4)
–3y2  –3(–4)2
= –3(16) = –48.
c. –3y3
–3y3  – 3(–4)3
= – 3(–64) = 192
Polynomial Expressions
Polynomial Expressions

23. b. –3y2 (y = –4)
–3y2  –3(–4)2
= –3(16) = –48.
c. –3y3
–3y3  – 3(–4)3
= – 3(–64) = 192
The sum of monomials are called polynomials (many-terms).
Polynomial Expressions
Polynomial Expressions

24. b. –3y2 (y = –4)
–3y2  –3(–4)2
= –3(16) = –48.
c. –3y3
–3y3  – 3(–4)3
= – 3(–64) = 192
The sum of monomials are called polynomials (many-terms).
These are expressions of the form, arranged in the order of
powers of the x: #xN ± #xN-1 ± … ± #x1 ± #
where the #’s are numbers.
Polynomial Expressions
Polynomial Expressions

25. b. –3y2 (y = –4)
–3y2  –3(–4)2
= –3(16) = –48.
c. –3y3
–3y3  – 3(–4)3
= – 3(–64) = 192
The sum of monomials are called polynomials (many-terms).
These are expressions of the form, arranged in the order of
powers of the x: #xN ± #xN-1 ± … ± #x1 ± #
where the #’s are numbers.
The highest exponent N is the degree of the polynomial.
Polynomial Expressions
Polynomial Expressions

26. b. –3y2 (y = –4)
–3y2  –3(–4)2
= –3(16) = –48.
c. –3y3
–3y3  – 3(–4)3
= – 3(–64) = 192
The sum of monomials are called polynomials (many-terms).
These are expressions of the form, arranged in the order of
powers of the x: #xN ± #xN-1 ± … ± #x1 ± #
where the #’s are numbers.
The highest exponent N is the degree of the polynomial.
For example, 4x – 7 is 1st degree (linear)
Polynomial Expressions
Polynomial Expressions

27. b. –3y2 (y = –4)
–3y2  –3(–4)2
= –3(16) = –48.
c. –3y3
–3y3  – 3(–4)3
= – 3(–64) = 192
The sum of monomials are called polynomials (many-terms).
These are expressions of the form, arranged in the order of
powers of the x: #xN ± #xN-1 ± … ± #x1 ± #
where the #’s are numbers.
The highest exponent N is the degree of the polynomial.
For example, 4x – 7 is 1st degree (linear)
and the degree of 1 – 3x2 – πx40 is 40.
Polynomial Expressions
Polynomial Expressions

28. b. –3y2 (y = –4)
–3y2  –3(–4)2
= –3(16) = –48.
c. –3y3
–3y3  – 3(–4)3
= – 3(–64) = 192
The sum of monomials are called polynomials (many-terms).
These are expressions of the form, arranged in the order of
powers of the x: #xN ± #xN-1 ± … ± #x1 ± #
where the #’s are numbers.
The highest exponent N is the degree of the polynomial.
For example, 4x – 7 is 1st degree (linear)
and the degree of 1 – 3x2 – πx40 is 40.
x
1 is not a polynomial.The expression
Polynomial Expressions
Polynomial Expressions

29. Example B. Evaluate the polynomial 4x2 – 3x3 if x = –3.
Polynomial Expressions

30. Example B. Evaluate the polynomial 4x2 – 3x3 if x = –3.
The polynomial 4x2 – 3x3 is the combination of two
monomials; 4x2 and –3x3.
Polynomial Expressions

31. Example B. Evaluate the polynomial 4x2 – 3x3 if x = –3.
The polynomial 4x2 – 3x3 is the combination of two
monomials; 4x2 and –3x3. When evaluating the polynomial,
we evaluate each monomial then combine the results.
Polynomial Expressions

32. Example B. Evaluate the polynomial 4x2 – 3x3 if x = –3.
The polynomial 4x2 – 3x3 is the combination of two
monomials; 4x2 and –3x3. When evaluating the polynomial,
we evaluate each monomial then combine the results.
Set x = (–3) in the expression,
Polynomial Expressions

33. Example B. Evaluate the polynomial 4x2 – 3x3 if x = –3.
The polynomial 4x2 – 3x3 is the combination of two
monomials; 4x2 and –3x3. When evaluating the polynomial,
we evaluate each monomial then combine the results.
Set x = (–3) in the expression, we get
4(–3)2 – 3(–3)3
Polynomial Expressions

34. Example B. Evaluate the polynomial 4x2 – 3x3 if x = –3.
The polynomial 4x2 – 3x3 is the combination of two
monomials; 4x2 and –3x3. When evaluating the polynomial,
we evaluate each monomial then combine the results.
Set x = (–3) in the expression, we get
4(–3)2 – 3(–3)3
= 4(9) – 3(–27)
Polynomial Expressions

35. Example B. Evaluate the polynomial 4x2 – 3x3 if x = –3.
The polynomial 4x2 – 3x3 is the combination of two
monomials; 4x2 and –3x3. When evaluating the polynomial,
we evaluate each monomial then combine the results.
Set x = (–3) in the expression, we get
4(–3)2 – 3(–3)3
= 4(9) – 3(–27)
= 36 + 81
= 117
Polynomial Expressions

36. Example B. Evaluate the polynomial 4x2 – 3x3 if x = –3.
The polynomial 4x2 – 3x3 is the combination of two
monomials; 4x2 and –3x3. When evaluating the polynomial,
we evaluate each monomial then combine the results.
Set x = (–3) in the expression, we get
4(–3)2 – 3(–3)3
= 4(9) – 3(–27)
= 36 + 81
= 117
Given a polynomial, each monomial is called a term.
Polynomial Expressions

37. Example B. Evaluate the polynomial 4x2 – 3x3 if x = –3.
The polynomial 4x2 – 3x3 is the combination of two
monomials; 4x2 and –3x3. When evaluating the polynomial,
we evaluate each monomial then combine the results.
Set x = (–3) in the expression, we get
4(–3)2 – 3(–3)3
= 4(9) – 3(–27)
= 36 + 81
= 117
Given a polynomial, each monomial is called a term.
#xN ± #xN-1 ± … ± #x ± #
terms
Polynomial Expressions

38. Example B. Evaluate the polynomial 4x2 – 3x3 if x = –3.
The polynomial 4x2 – 3x3 is the combination of two
monomials; 4x2 and –3x3. When evaluating the polynomial,
we evaluate each monomial then combine the results.
Set x = (–3) in the expression, we get
4(–3)2 – 3(–3)3
= 4(9) – 3(–27)
= 36 + 81
= 117
Given a polynomial, each monomial is called a term.
#xN ± #xN-1 ± … ± #x ± #
terms
Therefore the polynomial –3x2 – 4x + 7 has 3 terms,
–3x2 , –4x and + 7.
Polynomial Expressions

39. Each term is addressed by the variable part.
Polynomial Expressions

40. Each term is addressed by the variable part. Hence the
x2-term of the –3x2 – 4x + 7 is –3x2,
Polynomial Expressions

41. Each term is addressed by the variable part. Hence the
x2-term of the –3x2 – 4x + 7 is –3x2, the x-term is –4x,
Polynomial Expressions

42. Each term is addressed by the variable part. Hence the
x2-term of the –3x2 – 4x + 7 is –3x2, the x-term is –4x,
and the number term or the constant term is 7.
Polynomial Expressions

43. Each term is addressed by the variable part. Hence the
x2-term of the –3x2 – 4x + 7 is –3x2, the x-term is –4x,
and the number term or the constant term is 7.
The number in front of a term is called the coefficient of that
term.
Polynomial Expressions

44. Each term is addressed by the variable part. Hence the
x2-term of the –3x2 – 4x + 7 is –3x2, the x-term is –4x,
and the number term or the constant term is 7.
The number in front of a term is called the coefficient of that
term. So the coefficient of –3x2 is –3 .
Polynomial Expressions

45. Each term is addressed by the variable part. Hence the
x2-term of the –3x2 – 4x + 7 is –3x2, the x-term is –4x,
and the number term or the constant term is 7.
The number in front of a term is called the coefficient of that
term. So the coefficient of –3x2 is –3 .
Operations with Polynomials
Polynomial Expressions

46. Each term is addressed by the variable part. Hence the
x2-term of the –3x2 – 4x + 7 is –3x2, the x-term is –4x,
and the number term or the constant term is 7.
The number in front of a term is called the coefficient of that
term. So the coefficient of –3x2 is –3 .
Terms with the same variable part are called like-terms.
Operations with Polynomials
Polynomial Expressions

47. Each term is addressed by the variable part. Hence the
x2-term of the –3x2 – 4x + 7 is –3x2, the x-term is –4x,
and the number term or the constant term is 7.
The number in front of a term is called the coefficient of that
term. So the coefficient of –3x2 is –3 .
Terms with the same variable part are called like-terms.
Like-terms may be combined.
Operations with Polynomials
Polynomial Expressions

48. Each term is addressed by the variable part. Hence the
x2-term of the –3x2 – 4x + 7 is –3x2, the x-term is –4x,
and the number term or the constant term is 7.
The number in front of a term is called the coefficient of that
term. So the coefficient of –3x2 is –3 .
Terms with the same variable part are called like-terms.
Like-terms may be combined.
For example, 4x + 5x = 9x
Operations with Polynomials
Polynomial Expressions

49. Each term is addressed by the variable part. Hence the
x2-term of the –3x2 – 4x + 7 is –3x2, the x-term is –4x,
and the number term or the constant term is 7.
The number in front of a term is called the coefficient of that
term. So the coefficient of –3x2 is –3 .
Terms with the same variable part are called like-terms.
Like-terms may be combined.
For example, 4x + 5x = 9x and 3x2 – 5x2 = –2x2.
Operations with Polynomials
Polynomial Expressions

50. Each term is addressed by the variable part. Hence the
x2-term of the –3x2 – 4x + 7 is –3x2, the x-term is –4x,
and the number term or the constant term is 7.
The number in front of a term is called the coefficient of that
term. So the coefficient of –3x2 is –3 .
Terms with the same variable part are called like-terms.
Like-terms may be combined.
For example, 4x + 5x = 9x and 3x2 – 5x2 = –2x2.
Unlike terms may not be combined.
Operations with Polynomials
Polynomial Expressions

51. Each term is addressed by the variable part. Hence the
x2-term of the –3x2 – 4x + 7 is –3x2, the x-term is –4x,
and the number term or the constant term is 7.
The number in front of a term is called the coefficient of that
term. So the coefficient of –3x2 is –3 .
Terms with the same variable part are called like-terms.
Like-terms may be combined.
For example, 4x + 5x = 9x and 3x2 – 5x2 = –2x2.
Unlike terms may not be combined. So x + x2 stays as x + x2.
Operations with Polynomials
Polynomial Expressions

52. Each term is addressed by the variable part. Hence the
x2-term of the –3x2 – 4x + 7 is –3x2, the x-term is –4x,
and the number term or the constant term is 7.
The number in front of a term is called the coefficient of that
term. So the coefficient of –3x2 is –3 .
Terms with the same variable part are called like-terms.
Like-terms may be combined.
For example, 4x + 5x = 9x and 3x2 – 5x2 = –2x2.
Unlike terms may not be combined. So x + x2 stays as x + x2.
Note that we write 1xN as xN , –1xN as –xN.
Operations with Polynomials
Polynomial Expressions

53. Each term is addressed by the variable part. Hence the
x2-term of the –3x2 – 4x + 7 is –3x2, the x-term is –4x,
and the number term or the constant term is 7.
The number in front of a term is called the coefficient of that
term. So the coefficient of –3x2 is –3 .
Terms with the same variable part are called like-terms.
Like-terms may be combined.
For example, 4x + 5x = 9x and 3x2 – 5x2 = –2x2.
Unlike terms may not be combined. So x + x2 stays as x + x2.
Note that we write 1xN as xN , –1xN as –xN.
When multiplying a number with a term, we multiply it with the
coefficient.
Operations with Polynomials
Polynomial Expressions

54. Each term is addressed by the variable part. Hence the
x2-term of the –3x2 – 4x + 7 is –3x2, the x-term is –4x,
and the number term or the constant term is 7.
The number in front of a term is called the coefficient of that
term. So the coefficient of –3x2 is –3 .
Terms with the same variable part are called like-terms.
Like-terms may be combined.
For example, 4x + 5x = 9x and 3x2 – 5x2 = –2x2.
Unlike terms may not be combined. So x + x2 stays as x + x2.
Note that we write 1xN as xN , –1xN as –xN.
When multiplying a number with a term, we multiply it with the
coefficient. Hence, 3(5x) = (3*5)x
Operations with Polynomials
Polynomial Expressions

55. Each term is addressed by the variable part. Hence the
x2-term of the –3x2 – 4x + 7 is –3x2, the x-term is –4x,
and the number term or the constant term is 7.
The number in front of a term is called the coefficient of that
term. So the coefficient of –3x2 is –3 .
Terms with the same variable part are called like-terms.
Like-terms may be combined.
For example, 4x + 5x = 9x and 3x2 – 5x2 = –2x2.
Unlike terms may not be combined. So x + x2 stays as x + x2.
Note that we write 1xN as xN , –1xN as –xN.
When multiplying a number with a term, we multiply it with the
coefficient. Hence, 3(5x) = (3*5)x =15x,
Operations with Polynomials
Polynomial Expressions

56. Each term is addressed by the variable part. Hence the
x2-term of the –3x2 – 4x + 7 is –3x2, the x-term is –4x,
and the number term or the constant term is 7.
The number in front of a term is called the coefficient of that
term. So the coefficient of –3x2 is –3 .
Terms with the same variable part are called like-terms.
Like-terms may be combined.
For example, 4x + 5x = 9x and 3x2 – 5x2 = –2x2.
Unlike terms may not be combined. So x + x2 stays as x + x2.
Note that we write 1xN as xN , –1xN as –xN.
When multiplying a number with a term, we multiply it with the
coefficient. Hence, 3(5x) = (3*5)x =15x,
and –2(–4x) = (–2)(–4)x = 8x.
Operations with Polynomials
Polynomial Expressions

57. Each term is addressed by the variable part. Hence the
x2-term of the –3x2 – 4x + 7 is –3x2, the x-term is –4x,
and the number term or the constant term is 7.
The number in front of a term is called the coefficient of that
term. So the coefficient of –3x2 is –3 .
Terms with the same variable part are called like-terms.
Like-terms may be combined.
For example, 4x + 5x = 9x and 3x2 – 5x2 = –2x2.
Unlike terms may not be combined. So x + x2 stays as x + x2.
Note that we write 1xN as xN , –1xN as –xN.
When multiplying a number with a term, we multiply it with the
coefficient. Hence, 3(5x) = (3*5)x =15x,
and –2(–4x) = (–2)(–4)x = 8x.
Operations with Polynomials
When multiplying a number with a polynomial, we may
expand using the distributive law: A(B ± C) = AB ± AC.
Polynomial Expressions

58. Example C. Expand and simplify.
a. 3(2x – 4) + 2(4 – 5x)
Polynomial Expressions

59. Example C. Expand and simplify.
a. 3(2x – 4) + 2(4 – 5x)
= 6x – 12 + 8 – 10x
Polynomial Expressions

60. Example C. Expand and simplify.
a. 3(2x – 4) + 2(4 – 5x)
= 6x – 12 + 8 – 10x
= –4x – 4
Polynomial Expressions

61. Example C. Expand and simplify.
a. 3(2x – 4) + 2(4 – 5x)
= 6x – 12 + 8 – 10x
= –4x – 4
b. –3(x2 – 3x + 5) – 2(–x2 – 4x – 6)
Polynomial Expressions

62. Example C. Expand and simplify.
a. 3(2x – 4) + 2(4 – 5x)
= 6x – 12 + 8 – 10x
= –4x – 4
b. –3(x2 – 3x + 5) – 2(–x2 – 4x – 6)
= –3x2 + 9x – 15 + 2x2 + 8x +12
Polynomial Expressions

63. Example C. Expand and simplify.
a. 3(2x – 4) + 2(4 – 5x)
= 6x – 12 + 8 – 10x
= –4x – 4
b. –3(x2 – 3x + 5) – 2(–x2 – 4x – 6)
= –3x2 + 9x – 15 + 2x2 + 8x +12
= –x2 + 17x – 3
Polynomial Expressions

64. Example C. Expand and simplify.
a. 3(2x – 4) + 2(4 – 5x)
= 6x – 12 + 8 – 10x
= –4x – 4
b. –3(x2 – 3x + 5) – 2(–x2 – 4x – 6)
= –3x2 + 9x – 15 + 2x2 + 8x +12
= –x2 + 17x – 3
Polynomials in two or more variables.
Polynomial Expressions

65. Example C. Expand and simplify.
a. 3(2x – 4) + 2(4 – 5x)
= 6x – 12 + 8 – 10x
= –4x – 4
b. –3(x2 – 3x + 5) – 2(–x2 – 4x – 6)
= –3x2 + 9x – 15 + 2x2 + 8x +12
= –x2 + 17x – 3
Polynomials in two or more variables.
We form polynomials in two variables say, x & y, by adding
monomials of the form kx#y# where k is a number and the
powers are all nonnegative integers
Polynomial Expressions

66. Example C. Expand and simplify.
a. 3(2x – 4) + 2(4 – 5x)
= 6x – 12 + 8 – 10x
= –4x – 4
b. –3(x2 – 3x + 5) – 2(–x2 – 4x – 6)
= –3x2 + 9x – 15 + 2x2 + 8x +12
= –x2 + 17x – 3
Polynomials in two or more variables.
We form polynomials in two variables say, x & y, by adding
monomials of the form kx#y# where k is a number and the
powers are all nonnegative integers such as –5x3y2
Polynomial Expressions

67. Example C. Expand and simplify.
a. 3(2x – 4) + 2(4 – 5x)
= 6x – 12 + 8 – 10x
= –4x – 4
b. –3(x2 – 3x + 5) – 2(–x2 – 4x – 6)
= –3x2 + 9x – 15 + 2x2 + 8x +12
= –x2 + 17x – 3
Polynomials in two or more variables.
We form polynomials in two variables say, x & y, by adding
monomials of the form kx#y# where k is a number and the
powers are all nonnegative integers such as –5x3y2 or 3x2.
Polynomial Expressions

68. Example C. Expand and simplify.
a. 3(2x – 4) + 2(4 – 5x)
= 6x – 12 + 8 – 10x
= –4x – 4
b. –3(x2 – 3x + 5) – 2(–x2 – 4x – 6)
= –3x2 + 9x – 15 + 2x2 + 8x +12
= –x2 + 17x – 3
Polynomials in two or more variables.
We form polynomials in two variables say, x & y, by adding
monomials of the form kx#y# where k is a number and the
powers are all nonnegative integers such as –5x3y2 or 3x2.
Like–terms are terms where the variable parts are the same.
Polynomial Expressions

69. Example C. Expand and simplify.
a. 3(2x – 4) + 2(4 – 5x)
= 6x – 12 + 8 – 10x
= –4x – 4
b. –3(x2 – 3x + 5) – 2(–x2 – 4x – 6)
= –3x2 + 9x – 15 + 2x2 + 8x +12
= –x2 + 17x – 3
Polynomials in two or more variables.
We form polynomials in two variables say, x & y, by adding
monomials of the form kx#y# where k is a number and the
powers are all nonnegative integers such as –5x3y2 or 3x2.
Like–terms are terms where the variable parts are the same.
For example 3x2y3 + 5x2y3 = 8x2y3
Polynomial Expressions

70. Example C. Expand and simplify.
a. 3(2x – 4) + 2(4 – 5x)
= 6x – 12 + 8 – 10x
= –4x – 4
b. –3(x2 – 3x + 5) – 2(–x2 – 4x – 6)
= –3x2 + 9x – 15 + 2x2 + 8x +12
= –x2 + 17x – 3
Polynomials in two or more variables.
We form polynomials in two variables say, x & y, by adding
monomials of the form kx#y# where k is a number and the
powers are all nonnegative integers such as –5x3y2 or 3x2.
Like–terms are terms where the variable parts are the same.
For example 3x2y3 + 5x2y3 = 8x2y3 but 3x2y3 + 5x3y3 can’t be
combined.
Polynomial Expressions

71. Example C. Expand and simplify.
a. 3(2x – 4) + 2(4 – 5x)
= 6x – 12 + 8 – 10x
= –4x – 4
b. –3(x2 – 3x + 5) – 2(–x2 – 4x – 6)
= –3x2 + 9x – 15 + 2x2 + 8x +12
= –x2 + 17x – 3
Polynomials in two or more variables.
We form polynomials in two variables say, x & y, by adding
monomials of the form kx#y# where k is a number and the
powers are all nonnegative integers such as –5x3y2 or 3x2.
Like–terms are terms where the variable parts are the same.
For example 3x2y3 + 5x2y3 = 8x2y3 but 3x2y3 + 5x3y3 can’t be
combined. We evaluate them by assigning numbers to
x and/or y.
Polynomial Expressions

72. Example C. Expand and simplify.
a. 3(2x – 4) + 2(4 – 5x)
= 6x – 12 + 8 – 10x
= –4x – 4
b. –3(x2 – 3x + 5) – 2(–x2 – 4x – 6)
= –3x2 + 9x – 15 + 2x2 + 8x +12
= –x2 + 17x – 3
Polynomials in two or more variables.
We form polynomials in two variables say, x & y, by adding
monomials of the form kx#y# where k is a number and the
powers are all nonnegative integers such as –5x3y2 or 3x2.
Like–terms are terms where the variable parts are the same.
For example 3x2y3 + 5x2y3 = 8x2y3 but 3x2y3 + 5x3y3 can’t be
combined. We evaluate them by assigning numbers to
x and/or y. If only one number is given, the result is a formula.
Polynomial Expressions

73. Example C. Expand and simplify.
a. 3(2x – 4) + 2(4 – 5x)
= 6x – 12 + 8 – 10x
= –4x – 4
b. –3(x2 – 3x + 5) – 2(–x2 – 4x – 6)
= –3x2 + 9x – 15 + 2x2 + 8x +12
= –x2 + 17x – 3
Polynomials in two or more variables.
We form polynomials in two variables say, x & y, by adding
monomials of the form kx#y# where k is a number and the
powers are all nonnegative integers such as –5x3y2 or 3x2.
Like–terms are terms where the variable parts are the same.
For example 3x2y3 + 5x2y3 = 8x2y3 but 3x2y3 + 5x3y3 can’t be
combined. We evaluate them by assigning numbers to
x and/or y. If only one number is given, the result is a formula.
If both numbers are given, then we get a numerical output.
Polynomial Expressions

74. Example C. Expand and simplify.
a. 3(2x – 4) + 2(4 – 5x)
= 6x – 12 + 8 – 10x
= –4x – 4
b. –3(x2 – 3x + 5) – 2(–x2 – 4x – 6)
= –3x2 + 9x – 15 + 2x2 + 8x +12
= –x2 + 17x – 3
Polynomials in two or more variables.
We form polynomials in two variables say, x & y, by adding
monomials of the form kx#y# where k is a number and the
powers are all nonnegative integers such as –5x3y2 or 3x2.
Like–terms are terms where the variable parts are the same.
For example 3x2y3 + 5x2y3 = 8x2y3 but 3x2y3 + 5x3y3 can’t be
combined. We evaluate them by assigning numbers to
x and/or y. If only one number is given, the result is a formula.
If both numbers are given, then we get a numerical output.
We may do this for x, y and z or even more variables.
Polynomial Expressions

75. Example D. Expand and simplify.
a. 2(3xy – 4x2y) + 2xy – 3xy2
Polynomial Expressions

76. = 6xy – 8x2y + 2xy – 3xy2
Polynomial Expressions
Example D. Expand and simplify.
a. 2(3xy – 4x2y) + 2xy – 3xy2

77. Example D. Expand and simplify.
a. 2(3xy – 4x2y) + 2xy – 3xy2
= 6xy – 8x2y + 2xy – 3xy2
= 8xy – 8x2y – 3xy2
Polynomial Expressions

78. Example D. Expand and simplify.
a. 2(3xy – 4x2y) + 2xy – 3xy2
= 6xy – 8x2y + 2xy – 3xy2
= 8xy – 8x2y – 3xy2
b. Evaluate 8xy – 8x2y – 3xy2 if x = 2.
Polynomial Expressions

79. Example D. Expand and simplify.
a. 2(3xy – 4x2y) + 2xy – 3xy2
= 6xy – 8x2y + 2xy – 3xy2
= 8xy – 8x2y – 3xy2
b. Evaluate 8xy – 8x2y – 3xy2 if x = 2.
Input x = 2, we get 8(2)y – 8(2)2y – 3(2)y2
Polynomial Expressions

80. Example D. Expand and simplify.
a. 2(3xy – 4x2y) + 2xy – 3xy2
= 6xy – 8x2y + 2xy – 3xy2
= 8xy – 8x2y – 3xy2
b. Evaluate 8xy – 8x2y – 3xy2 if x = 2.
Input x = 2, we get 8(2)y – 8(2)2y – 3(2)y2
= 16y – 32y – 6y2
Polynomial Expressions

81. Example D. Expand and simplify.
a. 2(3xy – 4x2y) + 2xy – 3xy2
= 6xy – 8x2y + 2xy – 3xy2
= 8xy – 8x2y – 3xy2
b. Evaluate 8xy – 8x2y – 3xy2 if x = 2.
Input x = 2, we get 8(2)y – 8(2)2y – 3(2)y2
= 16y – 32y – 6y2
= –16y – 6y2
Polynomial Expressions

82. Example D. Expand and simplify.
a. 2(3xy – 4x2y) + 2xy – 3xy2
= 6xy – 8x2y + 2xy – 3xy2
= 8xy – 8x2y – 3xy2
b. Evaluate 8xy – 8x2y – 3xy2 if x = 2.
Input x = 2, we get 8(2)y – 8(2)2y – 3(2)y2
= 16y – 32y – 6y2
= –16y – 6y2
c. Evaluate 8xy – 8x2y – 3xy2 if x = 2 and y = 3
Polynomial Expressions

83. Example D. Expand and simplify.
a. 2(3xy – 4x2y) + 2xy – 3xy2
= 6xy – 8x2y + 2xy – 3xy2
= 8xy – 8x2y – 3xy2
b. Evaluate 8xy – 8x2y – 3xy2 if x = 2.
Input x = 2, we get 8(2)y – 8(2)2y – 3(2)y2
= 16y – 32y – 6y2
= –16y – 6y2
c. Evaluate 8xy – 8x2y – 3xy2 if x = 2 and y = 3
We may put x = 2, y = 3 into the formula and do everything
all over
Polynomial Expressions

84. Example D. Expand and simplify.
a. 2(3xy – 4x2y) + 2xy – 3xy2
= 6xy – 8x2y + 2xy – 3xy2
= 8xy – 8x2y – 3xy2
b. Evaluate 8xy – 8x2y – 3xy2 if x = 2.
Input x = 2, we get 8(2)y – 8(2)2y – 3(2)y2
= 16y – 32y – 6y2
= –16y – 6y2
c. Evaluate 8xy – 8x2y – 3xy2 if x = 2 and y = 3
We may put x = 2, y = 3 into the formula and do everything
all over again or we may plug into y = 3 into part b which is
easier.
Polynomial Expressions

85. Example D. Expand and simplify.
a. 2(3xy – 4x2y) + 2xy – 3xy2
= 6xy – 8x2y + 2xy – 3xy2
= 8xy – 8x2y – 3xy2
b. Evaluate 8xy – 8x2y – 3xy2 if x = 2.
Input x = 2, we get 8(2)y – 8(2)2y – 3(2)y2
= 16y – 32y – 6y2
= –16y – 6y2
c. Evaluate 8xy – 8x2y – 3xy2 if x = 2 and y = 3
We may put x = 2, y = 3 into the formula and do everything
all over again or we may plug into y = 3 into part b which is
easier. We will do the easy way.
Polynomial Expressions

86. Example D. Expand and simplify.
a. 2(3xy – 4x2y) + 2xy – 3xy2
= 6xy – 8x2y + 2xy – 3xy2
= 8xy – 8x2y – 3xy2
b. Evaluate 8xy – 8x2y – 3xy2 if x = 2.
Input x = 2, we get 8(2)y – 8(2)2y – 3(2)y2
= 16y – 32y – 6y2
= –16y – 6y2
c. Evaluate 8xy – 8x2y – 3xy2 if x = 2 and y = 3
We may put x = 2, y = 3 into the formula and do everything
all over again or we may plug into y = 3 into part b which is
easier. We will do the easy way.
Input y = 3 into –16y – 6y2
Polynomial Expressions

87. Example D. Expand and simplify.
a. 2(3xy – 4x2y) + 2xy – 3xy2
= 6xy – 8x2y + 2xy – 3xy2
= 8xy – 8x2y – 3xy2
b. Evaluate 8xy – 8x2y – 3xy2 if x = 2.
Input x = 2, we get 8(2)y – 8(2)2y – 3(2)y2
= 16y – 32y – 6y2
= –16y – 6y2
c. Evaluate 8xy – 8x2y – 3xy2 if x = 2 and y = 3
We may put x = 2, y = 3 into the formula and do everything
all over again or we may plug into y = 3 into part b which is
easier. We will do the easy way.
–16(3) – 6(3)2
Input y = 3 into –16y – 6y2
we get
Polynomial Expressions

88. Example D. Expand and simplify.
a. 2(3xy – 4x2y) + 2xy – 3xy2
= 6xy – 8x2y + 2xy – 3xy2
= 8xy – 8x2y – 3xy2
b. Evaluate 8xy – 8x2y – 3xy2 if x = 2.
Input x = 2, we get 8(2)y – 8(2)2y – 3(2)y2
= 16y – 32y – 6y2
= –16y – 6y2
c. Evaluate 8xy – 8x2y – 3xy2 if x = 2 and y = 3
We may put x = 2, y = 3 into the formula and do everything
all over again or we may plug into y = 3 into part b which is
easier. We will do the easy way.
–16(3) – 6(3)2
Input y = 3 into –16y – 6y2
we get
= –48 – 54 = –102
Polynomial Expressions

89. Ex. A. Evaluate each monomials with the given values.
3. 2x2 with x = 1 and x = –1 4. –2x2 with x = 1 and x = –1
5. 5y3 with y = 2 and y = –2 6. –5y3 with y = 2 and y = –2
1. 2x with x = 1 and x = –1 2. –2x with x = 1 and x = –1
7. 5z4 with z = 2 and z = –2 8. –5y4 with z = 2 and z = –2
B. Evaluate each monomials with the given values.
9. 2x2 – 3x + 2 with x = 1 and x = –1
10. –2x2 + 4x – 1 with x = 2 and x = –2
11. 3x2 – x – 2 with x = 3 and x = –3
12. –3x2 – x + 2 with x = 3 and x = –3
13. –2x3 – x2 + 4 with x = 2 and x = –2
14. –2x3 – 5x2 – 5 with x = 3 and x = –3
C. Expand and simplify.
15. 5(2x – 4) + 3(4 – 5x) 16. 5(2x – 4) – 3(4 – 5x)
17. –2(3x – 8) + 3(4 – 9x) 18. –2(3x – 8) – 3(4 – 9x)
19. 7(–2x – 7) – 3(4 – 3x) 20. –5(–2 – 8x) + 7(–2 – 11x)
Polynomial Expressions

90. 21. x2 – 3x + 5 + 2(–x2 – 4x – 6)
22. x2 – 3x + 5 – 2(–x2 – 4x – 6)
23. 2(x2 – 3x + 5) + 5(–x2 – 4x – 6)
24. 2(x2 – 3x + 5) – 5(–x2 – 4x – 6)
25. –2(3x2 – 2x + 5) + 5(–4x2 – 4x – 3)
26. –2(3x2 – 2x + 5) – 5(–4x2 – 4x – 3)
27. 4(3x3 – 5x2) – 9(6x2 – 7x) – 5(– 8x – 2)
29. Simplify 2(3xy – xy2) – 2(2xy – xy2) then evaluated it
with x = –1, afterwards evaluate it at (–1, 2) for (x, y)
30. Simplify x2 – 2(3xy – x2) – 2(y2 – xy) then evaluated it
with y = –2, afterwards evaluate it at (–1, –2) for (x, y)
31. Simplify x2 – 2(3xy – z2) – 2(z2 – x2) then evaluated it
with x = –1, y = – 2 and z = 3.
Polynomial Expressions
28. –6(7x2 + 5x – 9) – 7(–3x2 – 2x – 7)