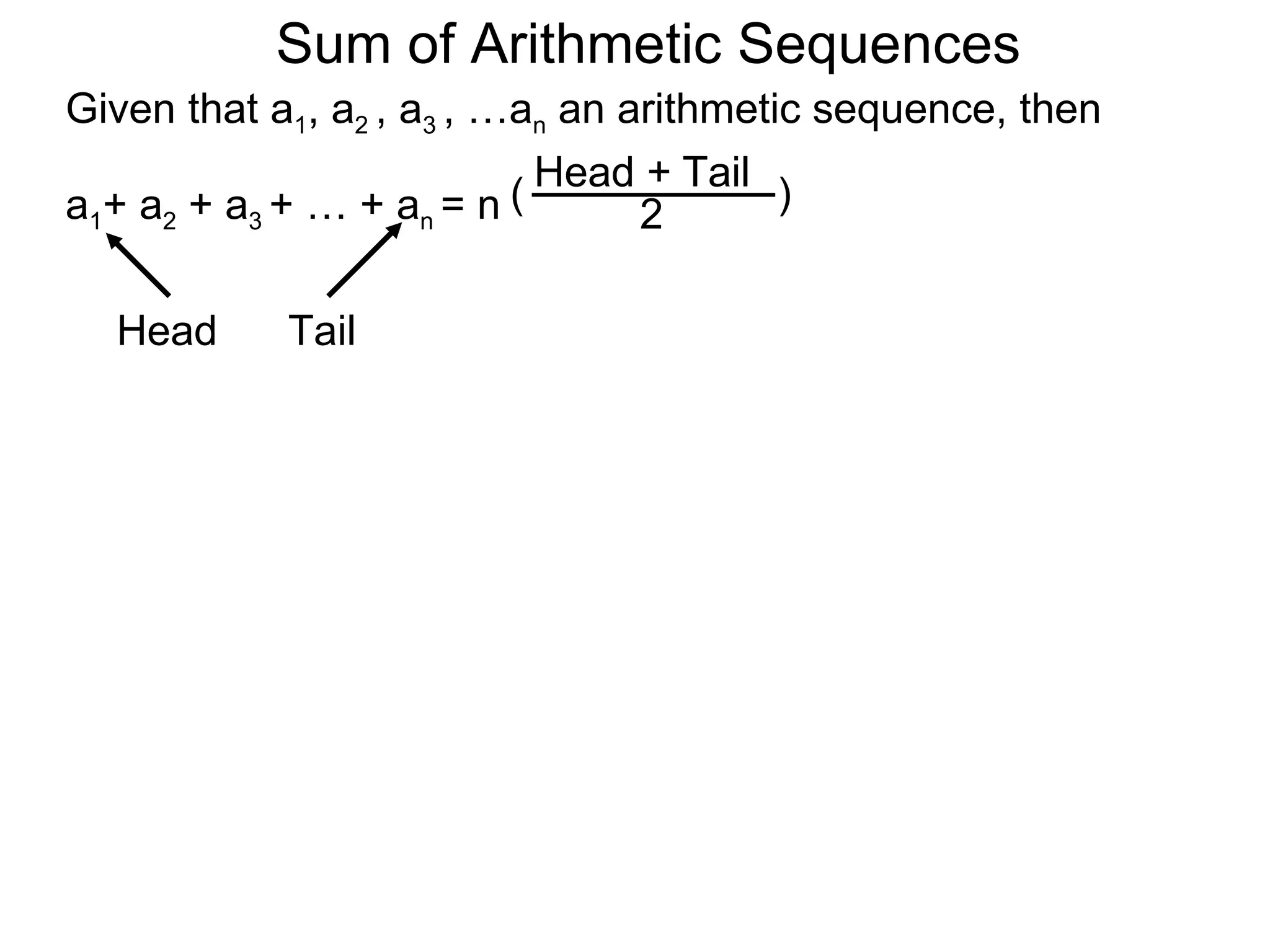
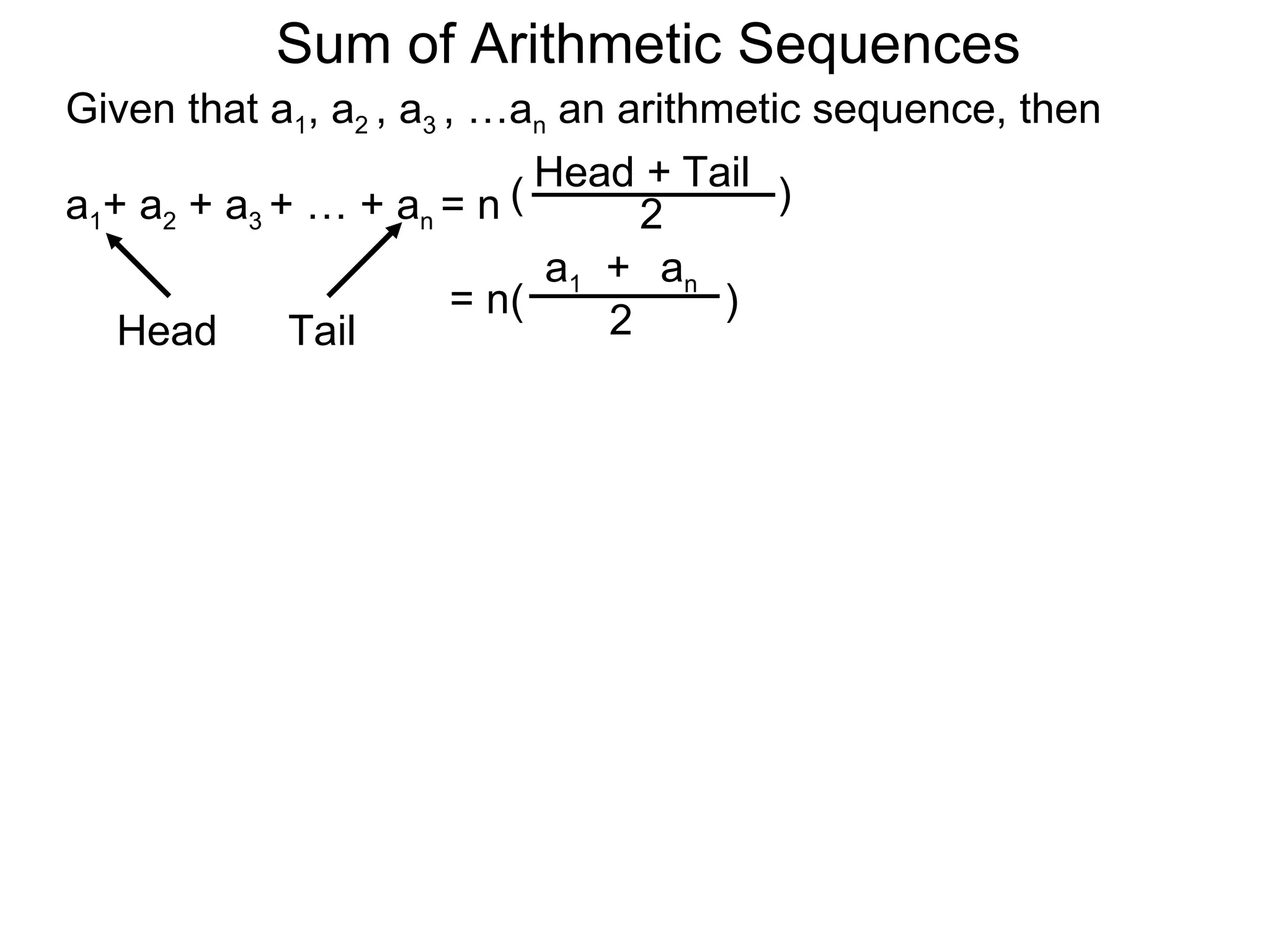
The document defines an arithmetic sequence as a sequence where the nth term is defined by a linear formula of the form an = d*n + c. It provides examples of arithmetic sequences and explains the general formula for finding any term in an arithmetic sequence if the first term (a1) and the common difference (d) between terms are known. It demonstrates using the general formula to find the specific formula for various arithmetic sequences given parts of the sequence.

1. Arithmetic Sequences

2. Arithmetic Sequences
A sequence a1, a2 , a3 , … is an arithmetic sequence
if an = d*n + c, i.e. it is defined by a linear formula.

3. Arithmetic Sequences
A sequence a1, a2 , a3 , … is an arithmetic sequence
if an = d*n + c, i.e. it is defined by a linear formula.
Example A. The sequence of odd numbers
a1= 1, a2= 3, a3= 5, a4= 7, …
is an arithmetic sequence because an = 2n – 1.

4. Arithmetic Sequences
A sequence a1, a2 , a3 , … is an arithmetic sequence
if an = d*n + c, i.e. it is defined by a linear formula.
Example A. The sequence of odd numbers
a1= 1, a2= 3, a3= 5, a4= 7, …
is an arithmetic sequence because an = 2n – 1.
Fact: If a1, a2 , a3 , …is an arithmetic sequence and that
an = d*n + c then the difference between any two terms is d,
i.e. ak+1 – ak = d.

5. Arithmetic Sequences
A sequence a1, a2 , a3 , … is an arithmetic sequence
if an = d*n + c, i.e. it is defined by a linear formula.
Example A. The sequence of odd numbers
a1= 1, a2= 3, a3= 5, a4= 7, …
is an arithmetic sequence because an = 2n – 1.
Fact: If a1, a2 , a3 , …is an arithmetic sequence and that
an = d*n + c then the difference between any two terms is d,
i.e. ak+1 – ak = d.
In example A, 3 – 1 = 5 – 3 = 7 – 5 = 2 = d.

6. Arithmetic Sequences
A sequence a1, a2 , a3 , … is an arithmetic sequence
if an = d*n + c, i.e. it is defined by a linear formula.
Example A. The sequence of odd numbers
a1= 1, a2= 3, a3= 5, a4= 7, …
is an arithmetic sequence because an = 2n – 1.
Fact: If a1, a2 , a3 , …is an arithmetic sequence and that
an = d*n + c then the difference between any two terms is d,
i.e. ak+1 – ak = d.
In example A, 3 – 1 = 5 – 3 = 7 – 5 = 2 = d.
The following theorem gives the converse of the above fact
and the main formula for arithmetic sequences.

7. Arithmetic Sequences
A sequence a1, a2 , a3 , … is an arithmetic sequence
if an = d*n + c, i.e. it is defined by a linear formula.
Example A. The sequence of odd numbers
a1= 1, a2= 3, a3= 5, a4= 7, …
is an arithmetic sequence because an = 2n – 1.
Fact: If a1, a2 , a3 , …is an arithmetic sequence and that
an = d*n + c then the difference between any two terms is d,
i.e. ak+1 – ak = d.
In example A, 3 – 1 = 5 – 3 = 7 – 5 = 2 = d.
The following theorem gives the converse of the above fact
and the main formula for arithmetic sequences.
Theorem: If a1, a2 , a3 , …an is a sequence such that
an+1 – an = d for all n, then a1, a2, a3,… is an arithmetic
sequence

8. Arithmetic Sequences
A sequence a1, a2 , a3 , … is an arithmetic sequence
if an = d*n + c, i.e. it is defined by a linear formula.
Example A. The sequence of odd numbers
a1= 1, a2= 3, a3= 5, a4= 7, …
is an arithmetic sequence because an = 2n – 1.
Fact: If a1, a2 , a3 , …is an arithmetic sequence and that
an = d*n + c then the difference between any two terms is d,
i.e. ak+1 – ak = d.
In example A, 3 – 1 = 5 – 3 = 7 – 5 = 2 = d.
The following theorem gives the converse of the above fact
and the main formula for arithmetic sequences.
Theorem: If a1, a2 , a3 , …an is a sequence such that
an+1 – an = d for all n, then a1, a2, a3,… is an arithmetic
sequence and the formula for the sequence is
an = d(n – 1) + a1.

9. Arithmetic Sequences
A sequence a1, a2 , a3 , … is an arithmetic sequence
if an = d*n + c, i.e. it is defined by a linear formula.
Example A. The sequence of odd numbers
a1= 1, a2= 3, a3= 5, a4= 7, …
is an arithmetic sequence because an = 2n – 1.
Fact: If a1, a2 , a3 , …is an arithmetic sequence and that
an = d*n + c then the difference between any two terms is d,
i.e. ak+1 – ak = d.
In example A, 3 – 1 = 5 – 3 = 7 – 5 = 2 = d.
The following theorem gives the converse of the above fact
and the main formula for arithmetic sequences.
Theorem: If a1, a2 , a3 , …an is a sequence such that
an+1 – an = d for all n, then a1, a2, a3,… is an arithmetic
sequence and the formula for the sequence is
an = d(n – 1) + a1. This is the general formula of arithemetic
sequences.

10. Arithmetic Sequences
Given the description of a arithmetic sequence, we use the
general formula to find the specific formula for that sequence.

11. Arithmetic Sequences
Given the description of a arithmetic sequence, we use the
general formula to find the specific formula for that sequence.
Example B. Given the sequence 2, 5, 8, 11, …
a. Verify it is an arithmetic sequence.

12. Arithmetic Sequences
Given the description of a arithmetic sequence, we use the
general formula to find the specific formula for that sequence.
Example B. Given the sequence 2, 5, 8, 11, …
a. Verify it is an arithmetic sequence.
It's arithmetic because 5 – 2 = 8 – 5 = 11 – 8 = … = 3 = d.

13. Arithmetic Sequences
Given the description of a arithmetic sequence, we use the
general formula to find the specific formula for that sequence.
Example B. Given the sequence 2, 5, 8, 11, …
a. Verify it is an arithmetic sequence.
It's arithmetic because 5 – 2 = 8 – 5 = 11 – 8 = … = 3 = d.
b. Find the (specific) formula represents this sequence.

14. Arithmetic Sequences
Given the description of a arithmetic sequence, we use the
general formula to find the specific formula for that sequence.
Example B. Given the sequence 2, 5, 8, 11, …
a. Verify it is an arithmetic sequence.
It's arithmetic because 5 – 2 = 8 – 5 = 11 – 8 = … = 3 = d.
b. Find the (specific) formula represents this sequence.
Plug a1 = 2 and d = 3, into the general formula
an = d(n – 1) + a1

15. Arithmetic Sequences
Given the description of a arithmetic sequence, we use the
general formula to find the specific formula for that sequence.
Example B. Given the sequence 2, 5, 8, 11, …
a. Verify it is an arithmetic sequence.
It's arithmetic because 5 – 2 = 8 – 5 = 11 – 8 = … = 3 = d.
b. Find the (specific) formula represents this sequence.
Plug a1 = 2 and d = 3, into the general formula
an = d(n – 1) + a1
we get
an = 3(n – 1) + 2

16. Arithmetic Sequences
Given the description of a arithmetic sequence, we use the
general formula to find the specific formula for that sequence.
Example B. Given the sequence 2, 5, 8, 11, …
a. Verify it is an arithmetic sequence.
It's arithmetic because 5 – 2 = 8 – 5 = 11 – 8 = … = 3 = d.
b. Find the (specific) formula represents this sequence.
Plug a1 = 2 and d = 3, into the general formula
an = d(n – 1) + a1
we get
an = 3(n – 1) + 2
an = 3n – 3 + 2

17. Arithmetic Sequences
Given the description of a arithmetic sequence, we use the
general formula to find the specific formula for that sequence.
Example B. Given the sequence 2, 5, 8, 11, …
a. Verify it is an arithmetic sequence.
It's arithmetic because 5 – 2 = 8 – 5 = 11 – 8 = … = 3 = d.
b. Find the (specific) formula represents this sequence.
Plug a1 = 2 and d = 3, into the general formula
an = d(n – 1) + a1
we get
an = 3(n – 1) + 2
an = 3n – 3 + 2
an = 3n – 1 the specific formula.

18. Arithmetic Sequences
Given the description of a arithmetic sequence, we use the
general formula to find the specific formula for that sequence.
Example B. Given the sequence 2, 5, 8, 11, …
a. Verify it is an arithmetic sequence.
It's arithmetic because 5 – 2 = 8 – 5 = 11 – 8 = … = 3 = d.
b. Find the (specific) formula represents this sequence.
Plug a1 = 2 and d = 3, into the general formula
an = d(n – 1) + a1
we get
an = 3(n – 1) + 2
an = 3n – 3 + 2
an = 3n – 1 the specific formula.
c. Find a1000.

19. Arithmetic Sequences
Given the description of a arithmetic sequence, we use the
general formula to find the specific formula for that sequence.
Example B. Given the sequence 2, 5, 8, 11, …
a. Verify it is an arithmetic sequence.
It's arithmetic because 5 – 2 = 8 – 5 = 11 – 8 = … = 3 = d.
b. Find the (specific) formula represents this sequence.
Plug a1 = 2 and d = 3, into the general formula
an = d(n – 1) + a1
we get
an = 3(n – 1) + 2
an = 3n – 3 + 2
an = 3n – 1 the specific formula.
c. Find a1000.
Set n = 1000 in the specific formula,

20. Arithmetic Sequences
Given the description of a arithmetic sequence, we use the
general formula to find the specific formula for that sequence.
Example B. Given the sequence 2, 5, 8, 11, …
a. Verify it is an arithmetic sequence.
It's arithmetic because 5 – 2 = 8 – 5 = 11 – 8 = … = 3 = d.
b. Find the (specific) formula represents this sequence.
Plug a1 = 2 and d = 3, into the general formula
an = d(n – 1) + a1
we get
an = 3(n – 1) + 2
an = 3n – 3 + 2
an = 3n – 1 the specific formula.
c. Find a1000.
Set n = 1000 in the specific formula, we get
a1000 = 3(1000) – 1 = 2999.

21. Arithmetic Sequences
To use the arithmetic general formula to find the specific
formula, we need the first term a1 and the difference d.

22. Arithmetic Sequences
To use the arithmetic general formula to find the specific
formula, we need the first term a1 and the difference d.
Example C. Given a1, a2 , a3 , …an arithmetic sequence with
d = -4 and a6 = 5, find a1, the specific formula and a1000.

23. Arithmetic Sequences
To use the arithmetic general formula to find the specific
formula, we need the first term a1 and the difference d.
Example C. Given a1, a2 , a3 , …an arithmetic sequence with
d = -4 and a6 = 5, find a1, the specific formula and a1000.
Set d = –4 in the general formula an = d(n – 1) + a1,

24. Arithmetic Sequences
To use the arithmetic general formula to find the specific
formula, we need the first term a1 and the difference d.
Example C. Given a1, a2 , a3 , …an arithmetic sequence with
d = -4 and a6 = 5, find a1, the specific formula and a1000.
Set d = –4 in the general formula an = d(n – 1) + a1, we get
an = –4(n – 1) + a1.

25. Arithmetic Sequences
To use the arithmetic general formula to find the specific
formula, we need the first term a1 and the difference d.
Example C. Given a1, a2 , a3 , …an arithmetic sequence with
d = -4 and a6 = 5, find a1, the specific formula and a1000.
Set d = –4 in the general formula an = d(n – 1) + a1, we get
an = –4(n – 1) + a1.
Set n = 6 in this formula,

26. Arithmetic Sequences
To use the arithmetic general formula to find the specific
formula, we need the first term a1 and the difference d.
Example C. Given a1, a2 , a3 , …an arithmetic sequence with
d = -4 and a6 = 5, find a1, the specific formula and a1000.
Set d = –4 in the general formula an = d(n – 1) + a1, we get
an = –4(n – 1) + a1.
Set n = 6 in this formula, we get
a6 = -4(6 – 1) + a1 = 5

27. Arithmetic Sequences
To use the arithmetic general formula to find the specific
formula, we need the first term a1 and the difference d.
Example C. Given a1, a2 , a3 , …an arithmetic sequence with
d = -4 and a6 = 5, find a1, the specific formula and a1000.
Set d = –4 in the general formula an = d(n – 1) + a1, we get
an = –4(n – 1) + a1.
Set n = 6 in this formula, we get
a6 = -4(6 – 1) + a1 = 5
-20 + a1 = 5

28. Arithmetic Sequences
To use the arithmetic general formula to find the specific
formula, we need the first term a1 and the difference d.
Example C. Given a1, a2 , a3 , …an arithmetic sequence with
d = -4 and a6 = 5, find a1, the specific formula and a1000.
Set d = –4 in the general formula an = d(n – 1) + a1, we get
an = –4(n – 1) + a1.
Set n = 6 in this formula, we get
a6 = -4(6 – 1) + a1 = 5
-20 + a1 = 5
a1 = 25

29. Arithmetic Sequences
To use the arithmetic general formula to find the specific
formula, we need the first term a1 and the difference d.
Example C. Given a1, a2 , a3 , …an arithmetic sequence with
d = -4 and a6 = 5, find a1, the specific formula and a1000.
Set d = –4 in the general formula an = d(n – 1) + a1, we get
an = –4(n – 1) + a1.
Set n = 6 in this formula, we get
a6 = -4(6 – 1) + a1 = 5
-20 + a1 = 5
a1 = 25
To find the specific formula , set 25 for a1 in an = -4(n – 1) + a1

30. Arithmetic Sequences
To use the arithmetic general formula to find the specific
formula, we need the first term a1 and the difference d.
Example C. Given a1, a2 , a3 , …an arithmetic sequence with
d = -4 and a6 = 5, find a1, the specific formula and a1000.
Set d = –4 in the general formula an = d(n – 1) + a1, we get
an = –4(n – 1) + a1.
Set n = 6 in this formula, we get
a6 = -4(6 – 1) + a1 = 5
-20 + a1 = 5
a1 = 25
To find the specific formula , set 25 for a1 in an = -4(n – 1) + a1
an = -4(n – 1) + 25

31. Arithmetic Sequences
To use the arithmetic general formula to find the specific
formula, we need the first term a1 and the difference d.
Example C. Given a1, a2 , a3 , …an arithmetic sequence with
d = -4 and a6 = 5, find a1, the specific formula and a1000.
Set d = –4 in the general formula an = d(n – 1) + a1, we get
an = –4(n – 1) + a1.
Set n = 6 in this formula, we get
a6 = -4(6 – 1) + a1 = 5
-20 + a1 = 5
a1 = 25
To find the specific formula , set 25 for a1 in an = -4(n – 1) + a1
an = -4(n – 1) + 25
an = -4n + 4 + 25

32. Arithmetic Sequences
To use the arithmetic general formula to find the specific
formula, we need the first term a1 and the difference d.
Example C. Given a1, a2 , a3 , …an arithmetic sequence with
d = -4 and a6 = 5, find a1, the specific formula and a1000.
Set d = –4 in the general formula an = d(n – 1) + a1, we get
an = –4(n – 1) + a1.
Set n = 6 in this formula, we get
a6 = -4(6 – 1) + a1 = 5
-20 + a1 = 5
a1 = 25
To find the specific formula , set 25 for a1 in an = -4(n – 1) + a1
an = -4(n – 1) + 25
an = -4n + 4 + 25
an = -4n + 29

33. Arithmetic Sequences
To use the arithmetic general formula to find the specific
formula, we need the first term a1 and the difference d.
Example C. Given a1, a2 , a3 , …an arithmetic sequence with
d = -4 and a6 = 5, find a1, the specific formula and a1000.
Set d = –4 in the general formula an = d(n – 1) + a1, we get
an = –4(n – 1) + a1.
Set n = 6 in this formula, we get
a6 = -4(6 – 1) + a1 = 5
-20 + a1 = 5
a1 = 25
To find the specific formula , set 25 for a1 in an = -4(n – 1) + a1
an = -4(n – 1) + 25
an = -4n + 4 + 25
an =find a1000, set n = 1000 in the specific formula
To -4n + 29

34. Arithmetic Sequences
To use the arithmetic general formula to find the specific
formula, we need the first term a1 and the difference d.
Example C. Given a1, a2 , a3 , …an arithmetic sequence with
d = -4 and a6 = 5, find a1, the specific formula and a1000.
Set d = –4 in the general formula an = d(n – 1) + a1, we get
an = –4(n – 1) + a1.
Set n = 6 in this formula, we get
a6 = -4(6 – 1) + a1 = 5
-20 + a1 = 5
a1 = 25
To find the specific formula , set 25 for a1 in an = -4(n – 1) + a1
an = -4(n – 1) + 25
an = -4n + 4 + 25
an =find a1000, set n = 1000 in the specific formula
To -4n + 29
a1000 = –4(1000) + 29 = –3971

35. Arithmetic Sequences
Example D. Given that a1, a2 , a3 , …is an arithmetic sequence
with a3 = -3 and a9 = 39, find d, a1 and the specific formula.

36. Arithmetic Sequences
Example D. Given that a1, a2 , a3 , …is an arithmetic sequence
with a3 = -3 and a9 = 39, find d, a1 and the specific formula.
Set n = 3 and n = 9 in the general arithmetic formula
an = d(n – 1) + a1,

37. Arithmetic Sequences
Example D. Given that a1, a2 , a3 , …is an arithmetic sequence
with a3 = -3 and a9 = 39, find d, a1 and the specific formula.
Set n = 3 and n = 9 in the general arithmetic formula
an = d(n – 1) + a1, we get
a3 = d(3 – 1) + a1 = -3

38. Arithmetic Sequences
Example D. Given that a1, a2 , a3 , …is an arithmetic sequence
with a3 = -3 and a9 = 39, find d, a1 and the specific formula.
Set n = 3 and n = 9 in the general arithmetic formula
an = d(n – 1) + a1, we get
a3 = d(3 – 1) + a1 = -3
2d + a1 = -3

39. Arithmetic Sequences
Example D. Given that a1, a2 , a3 , …is an arithmetic sequence
with a3 = -3 and a9 = 39, find d, a1 and the specific formula.
Set n = 3 and n = 9 in the general arithmetic formula
an = d(n – 1) + a1, we get
a9 = d(9 – 1) + a1 = 39
a3 = d(3 – 1) + a1 = -3
2d + a1 = -3

40. Arithmetic Sequences
Example D. Given that a1, a2 , a3 , …is an arithmetic sequence
with a3 = -3 and a9 = 39, find d, a1 and the specific formula.
Set n = 3 and n = 9 in the general arithmetic formula
an = d(n – 1) + a1, we get
a9 = d(9 – 1) + a1 = 39
a3 = d(3 – 1) + a1 = -3
8d + a1 = 39
2d + a1 = -3

41. Arithmetic Sequences
Example D. Given that a1, a2 , a3 , …is an arithmetic sequence
with a3 = -3 and a9 = 39, find d, a1 and the specific formula.
Set n = 3 and n = 9 in the general arithmetic formula
an = d(n – 1) + a1, we get
a9 = d(9 – 1) + a1 = 39
a3 = d(3 – 1) + a1 = -3
8d + a1 = 39
2d + a1 = -3
Subtract these equations:
8d + a1 = 39
) 2d + a1 = -3

42. Arithmetic Sequences
Example D. Given that a1, a2 , a3 , …is an arithmetic sequence
with a3 = -3 and a9 = 39, find d, a1 and the specific formula.
Set n = 3 and n = 9 in the general arithmetic formula
an = d(n – 1) + a1, we get
a9 = d(9 – 1) + a1 = 39
a3 = d(3 – 1) + a1 = -3
8d + a1 = 39
2d + a1 = -3
Subtract these equations:
8d + a1 = 39
) 2d + a1 = -3
6d = 42

43. Arithmetic Sequences
Example D. Given that a1, a2 , a3 , …is an arithmetic sequence
with a3 = -3 and a9 = 39, find d, a1 and the specific formula.
Set n = 3 and n = 9 in the general arithmetic formula
an = d(n – 1) + a1, we get
a9 = d(9 – 1) + a1 = 39
a3 = d(3 – 1) + a1 = -3
8d + a1 = 39
2d + a1 = -3
Subtract these equations:
8d + a1 = 39
) 2d + a1 = -3
6d = 42
d=7

44. Arithmetic Sequences
Example D. Given that a1, a2 , a3 , …is an arithmetic sequence
with a3 = -3 and a9 = 39, find d, a1 and the specific formula.
Set n = 3 and n = 9 in the general arithmetic formula
an = d(n – 1) + a1, we get
a9 = d(9 – 1) + a1 = 39
a3 = d(3 – 1) + a1 = -3
8d + a1 = 39
2d + a1 = -3
Subtract these equations:
8d + a1 = 39
) 2d + a1 = -3
6d = 42
d=7
Put d = 7 into 2d + a1 = -3,

45. Arithmetic Sequences
Example D. Given that a1, a2 , a3 , …is an arithmetic sequence
with a3 = -3 and a9 = 39, find d, a1 and the specific formula.
Set n = 3 and n = 9 in the general arithmetic formula
an = d(n – 1) + a1, we get
a9 = d(9 – 1) + a1 = 39
a3 = d(3 – 1) + a1 = -3
8d + a1 = 39
2d + a1 = -3
Subtract these equations:
8d + a1 = 39
) 2d + a1 = -3
6d = 42
d=7
Put d = 7 into 2d + a1 = -3,
2(7) + a1 = -3

46. Arithmetic Sequences
Example D. Given that a1, a2 , a3 , …is an arithmetic sequence
with a3 = -3 and a9 = 39, find d, a1 and the specific formula.
Set n = 3 and n = 9 in the general arithmetic formula
an = d(n – 1) + a1, we get
a9 = d(9 – 1) + a1 = 39
a3 = d(3 – 1) + a1 = -3
8d + a1 = 39
2d + a1 = -3
Subtract these equations:
8d + a1 = 39
) 2d + a1 = -3
6d = 42
d=7
Put d = 7 into 2d + a1 = -3,
2(7) + a1 = -3
14 + a1 = -3

47. Arithmetic Sequences
Example D. Given that a1, a2 , a3 , …is an arithmetic sequence
with a3 = -3 and a9 = 39, find d, a1 and the specific formula.
Set n = 3 and n = 9 in the general arithmetic formula
an = d(n – 1) + a1, we get
a9 = d(9 – 1) + a1 = 39
a3 = d(3 – 1) + a1 = -3
8d + a1 = 39
2d + a1 = -3
Subtract these equations:
8d + a1 = 39
) 2d + a1 = -3
6d = 42
d=7
Put d = 7 into 2d + a1 = -3,
2(7) + a1 = -3
14 + a1 = -3
a1 = -17

48. Arithmetic Sequences
Example D. Given that a1, a2 , a3 , …is an arithmetic sequence
with a3 = -3 and a9 = 39, find d, a1 and the specific formula.
Set n = 3 and n = 9 in the general arithmetic formula
an = d(n – 1) + a1, we get
a9 = d(9 – 1) + a1 = 39
a3 = d(3 – 1) + a1 = -3
8d + a1 = 39
2d + a1 = -3
Subtract these equations:
8d + a1 = 39
) 2d + a1 = -3
6d = 42
d=7
Put d = 7 into 2d + a1 = -3,
2(7) + a1 = -3
14 + a1 = -3
a1 = -17

49. Arithmetic Sequences
Example D. Given that a1, a2 , a3 , …is an arithmetic sequence
with a3 = -3 and a9 = 39, find d, a1 and the specific formula.
Set n = 3 and n = 9 in the general arithmetic formula
an = d(n – 1) + a1, we get
a9 = d(9 – 1) + a1 = 39
a3 = d(3 – 1) + a1 = -3
8d + a1 = 39
2d + a1 = -3
Subtract these equations:
8d + a1 = 39
) 2d + a1 = -3
6d = 42
d=7
Put d = 7 into 2d + a1 = -3,
2(7) + a1 = -3
14 + a1 = -3
a1 = -17

50. Sum of Arithmetic Sequences
Given that a1, a2 , a3 , …an an arithmetic sequence, then
( Head 2 Tail )
+
a1+ a2 + a3 + … + an = n

51. Sum of Arithmetic Sequences
Given that a1, a2 , a3 , …an an arithmetic sequence, then
( Head 2 Tail )
+
a1+ a2 + a3 + … + an = n
Head Tail

52. Sum of Arithmetic Sequences
Given that a1, a2 , a3 , …an an arithmetic sequence, then
( Head 2 Tail )
+
a1+ a2 + a3 + … + an = n
a1 + an
= n( )
Head Tail 2

53. Sum of Arithmetic Sequences
Given that a1, a2 , a3 , …an an arithmetic sequence, then
( Head 2 Tail )
+
a1+ a2 + a3 + … + an = n
a1 + an
= n( )
Head Tail 2
Example E.
a. Given the arithmetic sequence a1= 4, 7, 10, … , and
an = 67. What is n?

54. Sum of Arithmetic Sequences
Given that a1, a2 , a3 , …an an arithmetic sequence, then
( Head 2 Tail )
+
a1+ a2 + a3 + … + an = n
a1 + an
= n( )
Head Tail 2
Example E.
a. Given the arithmetic sequence a1= 4, 7, 10, … , and
an = 67. What is n?
We need the specific formula.

55. Sum of Arithmetic Sequences
Given that a1, a2 , a3 , …an an arithmetic sequence, then
( Head 2 Tail )
+
a1+ a2 + a3 + … + an = n
a1 + an
= n( )
Head Tail 2
Example E.
a. Given the arithmetic sequence a1= 4, 7, 10, … , and
an = 67. What is n?
We need the specific formula. Find d = 7 – 4 = 3.

56. Sum of Arithmetic Sequences
Given that a1, a2 , a3 , …an an arithmetic sequence, then
( Head 2 Tail )
+
a1+ a2 + a3 + … + an = n
a1 + an
= n( )
Head Tail 2
Example E.
a. Given the arithmetic sequence a1= 4, 7, 10, … , and
an = 67. What is n?
We need the specific formula. Find d = 7 – 4 = 3.
Therefore the specific formula is
an = 3(n – 1) + 4

57. Sum of Arithmetic Sequences
Given that a1, a2 , a3 , …an an arithmetic sequence, then
( Head 2 Tail )
+
a1+ a2 + a3 + … + an = n
a1 + an
= n( )
Head Tail 2
Example E.
a. Given the arithmetic sequence a1= 4, 7, 10, … , and
an = 67. What is n?
We need the specific formula. Find d = 7 – 4 = 3.
Therefore the specific formula is
an = 3(n – 1) + 4
an = 3n + 1.

58. Sum of Arithmetic Sequences
Given that a1, a2 , a3 , …an an arithmetic sequence, then
( Head 2 Tail )
+
a1+ a2 + a3 + … + an = n
a1 + an
= n( )
Head Tail 2
Example E.
a. Given the arithmetic sequence a1= 4, 7, 10, … , and
an = 67. What is n?
We need the specific formula. Find d = 7 – 4 = 3.
Therefore the specific formula is
an = 3(n – 1) + 4
an = 3n + 1.
If an = 67 = 3n + 1,

59. Sum of Arithmetic Sequences
Given that a1, a2 , a3 , …an an arithmetic sequence, then
( Head 2 Tail )
+
a1+ a2 + a3 + … + an = n
a1 + an
= n( )
Head Tail 2
Example E.
a. Given the arithmetic sequence a1= 4, 7, 10, … , and
an = 67. What is n?
We need the specific formula. Find d = 7 – 4 = 3.
Therefore the specific formula is
an = 3(n – 1) + 4
an = 3n + 1.
If an = 67 = 3n + 1, then
66 = 3n

60. Sum of Arithmetic Sequences
Given that a1, a2 , a3 , …an an arithmetic sequence, then
( Head 2 Tail )
+
a1+ a2 + a3 + … + an = n
a1 + an
= n( )
Head Tail 2
Example E.
a. Given the arithmetic sequence a1= 4, 7, 10, … , and
an = 67. What is n?
We need the specific formula. Find d = 7 – 4 = 3.
Therefore the specific formula is
an = 3(n – 1) + 4
an = 3n + 1.
If an = 67 = 3n + 1, then
66 = 3n
or 22 = n

61. Sum of Arithmetic Sequences
b. Find the sum 4 + 7 + 10 +…+ 67

62. Sum of Arithmetic Sequences
b. Find the sum 4 + 7 + 10 +…+ 67
a1 = 4, and a22 = 67 with n = 22,

63. Sum of Arithmetic Sequences
b. Find the sum 4 + 7 + 10 +…+ 67
a1 = 4, and a22 = 67 with n = 22, so the sum
4 + 67
4 + 7 + 10 +…+ 67 = 22 ( 2 )

64. Sum of Arithmetic Sequences
b. Find the sum 4 + 7 + 10 +…+ 67
a1 = 4, and a22 = 67 with n = 22, so the sum
11 4 + 67
4 + 7 + 10 +…+ 67 = 22 ( 2 )

65. Sum of Arithmetic Sequences
b. Find the sum 4 + 7 + 10 +…+ 67
a1 = 4, and a22 = 67 with n = 22, so the sum
11 4 + 67
4 + 7 + 10 +…+ 67 = 22 ( 2 ) = 11(71)

66. Sum of Arithmetic Sequences
b. Find the sum 4 + 7 + 10 +…+ 67
a1 = 4, and a22 = 67 with n = 22, so the sum
11 4 + 67
4 + 7 + 10 +…+ 67 = 22 ( 2 ) = 11(71) = 781

67. Arithmetic Sequences

68. Sum of Arithmetic Sequences
Find the specific formula then the arithmetic sum.
a. – 4 – 1 + 2 +…+ 302
b. – 4 – 9 – 14 … – 1999
c. 27 + 24 + 21 … – 1992
d. 3 + 9 + 15 … + 111,111,111