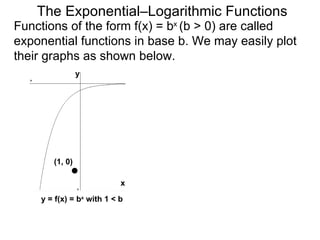
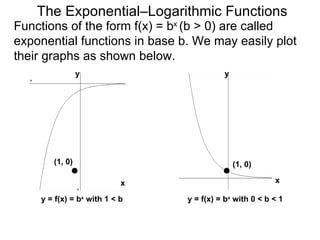
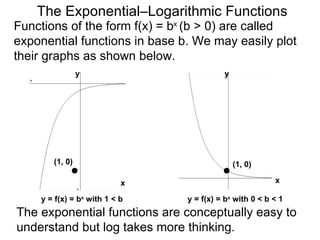
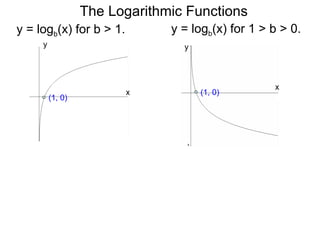
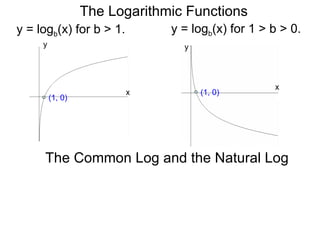
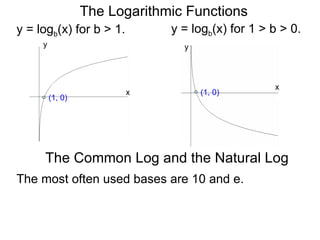
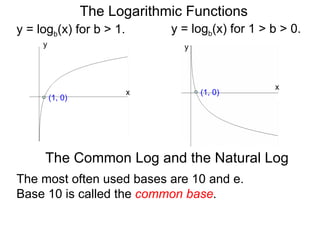
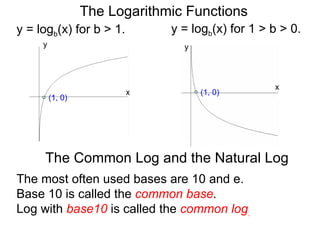
The document discusses exponential and logarithmic functions. Exponential functions of the form f(x) = b^x are called exponential functions in base b. Logarithmic functions log_b(y) represent the exponent x needed to raise the base b to a power to get the output y. The exponential form b^x = y and logarithmic form x = log_b(y) describe the same relationship between the base b, exponent x, and output y. Questions can be translated between these forms by rewriting the exponential expression as a logarithm or vice versa. Examples demonstrate rewriting expressions and graphing logarithmic functions.

1. The Exponential–Logarithmic Functions Functions of the form f(x) = b x (b > 0) are called exponential functions in base b.

2. The Exponential–Logarithmic Functions Functions of the form f(x) = b x (b > 0) are called exponential functions in base b. We may easily plot their graphs as shown below.

3. The Exponential–Logarithmic Functions Functions of the form f(x) = b x (b > 0) are called exponential functions in base b. We may easily plot their graphs as shown below. x y y = f(x) = b x with 1 < b (1, 0)

4. The Exponential–Logarithmic Functions Functions of the form f(x) = b x (b > 0) are called exponential functions in base b. We may easily plot their graphs as shown below. x y x y y = f(x) = b x with 1 < b y = f(x) = b x with 0 < b < 1 (1, 0) (1, 0)

5. The Exponential–Logarithmic Functions Functions of the form f(x) = b x (b > 0) are called exponential functions in base b. We may easily plot their graphs as shown below. x y x y y = f(x) = b x with 1 < b y = f(x) = b x with 0 < b < 1 (1, 0) (1, 0) The exponential functions are conceptually easy to understand but log takes more thinking.

6. The Exponential–Logarithmic Functions Functions of the form f(x) = b x (b > 0) are called exponential functions in base b.

7. The Exponential–Logarithmic Functions Functions of the form f(x) = b x (b > 0) are called exponential functions in base b. Let f(x) = y = 2 x , the base–2 exponential function, at x = 3 we have that 2 3 = 8

8. The Exponential–Logarithmic Functions Functions of the form f(x) = b x (b > 0) are called exponential functions in base b. Let f(x) = y = 2 x , the base–2 exponential function, at x = 3 we have that 2 3 = 8 or the “(base) 2 raised to the power 3 gives 8”.

9. The Exponential–Logarithmic Functions Functions of the form f(x) = b x (b > 0) are called exponential functions in base b. Let f(x) = y = 2 x , the base–2 exponential function, at x = 3 we have that 2 3 = 8 or the “(base) 2 raised to the power 3 gives 8”. The relation 2 3 = 8 between 2, 3, and 8 expressed in this manner is said to be in the exponential form .

10. The Exponential–Logarithmic Functions Functions of the form f(x) = b x (b > 0) are called exponential functions in base b. Let f(x) = y = 2 x , the base–2 exponential function, at x = 3 we have that 2 3 = 8 or the “(base) 2 raised to the power 3 gives 8”. The relation 2 3 = 8 between 2, 3, and 8 expressed in this manner is said to be in the exponential form . In the exponential form the focus is the outcome of “taking 2 to the whatever–power”.

11. The Exponential–Logarithmic Functions Functions of the form f(x) = b x (b > 0) are called exponential functions in base b. Let f(x) = y = 2 x , the base–2 exponential function, at x = 3 we have that 2 3 = 8 or the “(base) 2 raised to the power 3 gives 8”. The relation 2 3 = 8 between 2, 3, and 8 expressed in this manner is said to be in the exponential form . In the exponential form the focus is the outcome of “taking 2 to the whatever–power”. But if we want to find the exponent and ask instead “given that the outcome is 8 in raising 2 to a power, what was the power p ?” i.e. 2 p = 8,

12. The Exponential–Logarithmic Functions Functions of the form f(x) = b x (b > 0) are called exponential functions in base b. Let f(x) = y = 2 x , the base–2 exponential function, at x = 3 we have that 2 3 = 8 or the “(base) 2 raised to the power 3 gives 8”. The relation 2 3 = 8 between 2, 3, and 8 expressed in this manner is said to be in the exponential form . In the exponential form the focus is the outcome of “taking 2 to the whatever–power”. But if we want to find the exponent and ask instead “given that the outcome is 8 in raising 2 to a power, what was the power p ?” i.e. 2 p = 8, this question is written as “log 2 ( 8 ) = p ”

13. The Exponential–Logarithmic Functions Functions of the form f(x) = b x (b > 0) are called exponential functions in base b. Let f(x) = y = 2 x , the base–2 exponential function, at x = 3 we have that 2 3 = 8 or the “(base) 2 raised to the power 3 gives 8”. The relation 2 3 = 8 between 2, 3, and 8 expressed in this manner is said to be in the exponential form . In the exponential form the focus is the outcome of “taking 2 to the whatever–power”. But if we want to find the exponent and ask instead “given that the outcome is 8 in raising 2 to a power, what was the power p ?” i.e. 2 p = 8, this question is written as “log 2 ( 8 ) = p ” and of course log 2 ( 8 ) = 3 .

14. The Exponential–Logarithmic Functions Functions of the form f(x) = b x (b > 0) are called exponential functions in base b. Let f(x) = y = 2 x , the base–2 exponential function, at x = 3 we have that 2 3 = 8 or the “(base) 2 raised to the power 3 gives 8”. The relation 2 3 = 8 between 2, 3, and 8 expressed in this manner is said to be in the exponential form . In the exponential form the focus is the outcome of “taking 2 to the whatever–power”. But if we want to find the exponent and ask instead “given that the outcome is 8 in raising 2 to a power, what was the power p ?” i.e. 2 p = 8, this question is written as “log 2 ( 8 ) = p ” and of course log 2 ( 8 ) = 3 . The base–power–output relation between 2, 3, and 8 expressed as log 2 (8) = 3 is said to be in the log–form .

15. The Logarithmic Functions The log b (y) represents the exponent x where x is the exponent needed (with base b) to get y.

16. The Logarithmic Functions The log b (y) represents the exponent x where x is the exponent needed (with base b) to get y. The exponential form b x = y and the log–form x = log b (y) describe the same relation between the numbers b, x and y.

17. The Logarithmic Functions The log b (y) represents the exponent x where x is the exponent needed (with base b) to get y. The exponential form b x = y and the log–form x = log b (y) describe the same relation between the numbers b, x and y. Questions stated in one form often need to be translated into the other form before solving.

18. The Logarithmic Functions The log b (y) represents the exponent x where x is the exponent needed (with base b) to get y. The exponential form b x = y and the log–form x = log b (y) describe the same relation between the numbers b, x and y. Questions stated in one form often need to be translated into the other form before solving. In these situations, always identify the base number b first.

19. The Logarithmic Functions The log b (y) represents the exponent x where x is the exponent needed (with base b) to get y. The exponential form b x = y and the log–form x = log b (y) describe the same relation between the numbers b, x and y. Questions stated in one form often need to be translated into the other form before solving. In these situations, always identify the base number b first. Example B. Rewrite the exp-form into the log-form. a. 4 2 = 16 b. w = u 2+v

20. The Logarithmic Functions The log b (y) represents the exponent x where x is the exponent needed (with base b) to get y. The exponential form b x = y and the log–form x = log b (y) describe the same relation between the numbers b, x and y. Questions stated in one form often need to be translated into the other form before solving. In these situations, always identify the base number b first. Example B. Rewrite the exp-form into the log-form. a. 4 2 = 16  2 = log 4 (16) b. w = u 2+v

21. The Logarithmic Functions The log b (y) represents the exponent x where x is the exponent needed (with base b) to get y. The exponential form b x = y and the log–form x = log b (y) describe the same relation between the numbers b, x and y. Questions stated in one form often need to be translated into the other form before solving. In these situations, always identify the base number b first. Example B. Rewrite the exp-form into the log-form. a. 4 2 = 16  2 = log 4 (16) b. w = u 2+v  log u (w) = 2+v

22. The Logarithmic Functions The log b (y) represents the exponent x where x is the exponent needed (with base b) to get y. The exponential form b x = y and the log–form x = log b (y) describe the same relation between the numbers b, x and y. Questions stated in one form often need to be translated into the other form before solving. In these situations, always identify the base number b first. Example C. Rewrite the log-form into the exp-form. a. log 3 (1/9) = b. 2w = Example B. Rewrite the exp-form into the log-form. a. 4 2 = 16  2 = log 4 (16) b. w = u 2+v  log u (w) = 2+v

23. The Logarithmic Functions The log b (y) represents the exponent x where x is the exponent needed (with base b) to get y. The exponential form b x = y and the log–form x = log b (y) describe the same relation between the numbers b, x and y. Questions stated in one form often need to be translated into the other form before solving. In these situations, always identify the base number b first. Example C. Rewrite the log-form into the exp-form. a. log 3 (1/9) = – 2  1/9 = 3 -2 b. 2w = Example B. Rewrite the exp-form into the log-form. a. 4 2 = 16  2 = log 4 (16) b. w = u 2+v  log u (w) = 2+v

24. The Logarithmic Functions The log b (y) represents the exponent x where x is the exponent needed (with base b) to get y. The exponential form b x = y and the log–form x = log b (y) describe the same relation between the numbers b, x and y. Questions stated in one form often need to be translated into the other form before solving. In these situations, always identify the base number b first. Example C. Rewrite the log-form into the exp-form. a. log 3 (1/9) = – 2  1/9 = 3 -2 b. 2w = log v (a – b)  a – b = v 2w Example B. Rewrite the exp-form into the log-form. a. 4 2 = 16  2 = log 4 (16) b. w = u 2+v  log u (w) = 2+v

25. The domain of log b (y) is the set of all y > 0. The Logarithmic Functions

26. The domain of log b (y) is the set of all y > 0. For example, log 2 (–1) doesn't exist because there is no exponent p such that 2 p = –1. The Logarithmic Functions

27. The domain of log b (y) is the set of all y > 0. For example, log 2 (–1) doesn't exist because there is no exponent p such that 2 p = –1. We use the variables u and v for the next graph. The Logarithmic Functions

28. The domain of log b (y) is the set of all y > 0. For example, log 2 (–1) doesn't exist because there is no exponent p such that 2 p = –1. We use the variables u and v for the next graph. The Logarithmic Functions Example D. Make a table and graph u = log 2 (v).

29. The domain of log b (y) is the set of all y > 0. For example, log 2 (–1) doesn't exist because there is no exponent p such that 2 p = –1. We use the variables u and v for the next graph. The Logarithmic Functions u v=log 2 (u) Example D. Make a table and graph u = log 2 (v).

30. The domain of log b (y) is the set of all y > 0. For example, log 2 (–1) doesn't exist because there is no exponent p such that 2 p = –1. We use the variables u and v for the next graph. The Logarithmic Functions u v=log 2 (u) Example D. Make a table and graph u = log 2 (v). 1/4 1/2 1 2 4 8

31. The domain of log b (y) is the set of all y > 0. For example, log 2 (–1) doesn't exist because there is no exponent p such that 2 p = –1. We use the variables u and v for the next graph. The Logarithmic Functions u v=log 2 (u) Example D. Make a table and graph u = log 2 (v). 1/4 1/2 1 2 4 8 3

32. The domain of log b (y) is the set of all y > 0. For example, log 2 (–1) doesn't exist because there is no exponent p such that 2 p = –1. We use the variables u and v for the next graph. The Logarithmic Functions u v=log 2 (u) Example D. Make a table and graph u = log 2 (v). 1/4 1/2 1 2 1 4 2 8 3

33. The domain of log b (y) is the set of all y > 0. For example, log 2 (–1) doesn't exist because there is no exponent p such that 2 p = –1. We use the variables u and v for the next graph. The Logarithmic Functions u v=log 2 (u) Example D. Make a table and graph u = log 2 (v). 1/4 -2 1/2 -1 1 0 2 1 4 2 8 3

34. The domain of log b (y) is the set of all y > 0. For example, log 2 (–1) doesn't exist because there is no exponent p such that 2 p = –1. We use the variables u and v for the next graph. The Logarithmic Functions u v=log 2 (u) Example D. Make a table and graph u = log 2 (v). 1/4 -2 1/2 -1 1 0 2 1 4 2 8 3

35. y = log b (x) for b > 1. The Logarithmic Functions y x (1, 0)

36. y = log b (x) for b > 1. The Logarithmic Functions y = log b (x) for 1 > b > 0. y x x y (1, 0) (1, 0)

37. y = log b (x) for b > 1. The Logarithmic Functions y = log b (x) for 1 > b > 0. y x x y (1, 0) (1, 0) The Common Log and the Natural Log

38. y = log b (x) for b > 1. The Logarithmic Functions y = log b (x) for 1 > b > 0. y x x y (1, 0) (1, 0) The most often used bases are 10 and e. The Common Log and the Natural Log

39. y = log b (x) for b > 1. The Logarithmic Functions y = log b (x) for 1 > b > 0. y x x y (1, 0) (1, 0) The most often used bases are 10 and e. Base 10 is called the common base . The Common Log and the Natural Log

40. y = log b (x) for b > 1. The Logarithmic Functions y = log b (x) for 1 > b > 0. y x x y (1, 0) (1, 0) The most often used bases are 10 and e. Base 10 is called the common base . Log with base10 is called the common log . The Common Log and the Natural Log

41. y = log b (x) for b > 1. The Logarithmic Functions y = log b (x) for 1 > b > 0. y x x y (1, 0) (1, 0) The most often used bases are 10 and e. Base 10 is called the common base . Log with base10 is called the common log . It is written as log(x) without the base number b. The Common Log and the Natural Log

42. Base e is called the natural base . The Common Log and the Natural Log

43. Base e is called the natural base . Log with base e is called the natural log . The Common Log and the Natural Log

44. Base e is called the natural base . Log with base e is called the natural log . It is written as ln(x) . The Common Log and the Natural Log

45. Base e is called the natural base . Log with base e is called the natural log . It is written as ln(x) . The Common Log and the Natural Log Example E. Convert to the other form. A P exp-form log-form 10 3 = 1000 ln( 1/e 2 ) = -2 e rt = l og ( 1 ) = 0

46. Base e is called the natural base . Log with base e is called the natural log . It is written as ln(x) . The Common Log and the Natural Log Example E. Convert to the other form. A P exp-form log-form 10 3 = 1000 log( 1000 ) = 3 ln( 1/e 2 ) = -2 e rt = l og ( 1 ) = 0

47. Base e is called the natural base . Log with base e is called the natural log . It is written as ln(x) . The Common Log and the Natural Log Example E. Convert to the other form. A P exp-form log-form 10 3 = 1000 log( 1000 ) = 3 e -2 = 1/e 2 ln( 1/e 2 ) = -2 e rt = l og ( 1 ) = 0

48. Base e is called the natural base . Log with base e is called the natural log . It is written as ln(x) . The Common Log and the Natural Log Example E. Convert to the other form. A P A P exp-form log-form 10 3 = 1000 log( 1000 ) = 3 e -2 = 1/e 2 ln( 1/e 2 ) = -2 e rt = ln( ) = rt l og ( 1 ) = 0

49. Base e is called the natural base . Log with base e is called the natural log . It is written as ln(x) . The Common Log and the Natural Log Example E. Convert to the other form. A P A P exp-form log-form 10 3 = 1000 log( 1000 ) = 3 e -2 = 1/e 2 ln( 1/e 2 ) = -2 e rt = ln( ) = rt 10 0 = 1 l og ( 1 ) = 0

50. When we change the log-form into the exp-form, we say we &quot;drop the log&quot;. The Common Log and the Natural Log

51. Example F. Solve for x. a. log 9 (x) = -1 b. log x (9) = -2 When we change the log-form into the exp-form, we say we &quot;drop the log&quot;. The Common Log and the Natural Log

52. Example F. Solve for x. a. log 9 (x) = -1 Drop the log and get x = 9 -1 . b. log x (9) = -2 When we change the log-form into the exp-form, we say we &quot;drop the log&quot;. The Common Log and the Natural Log

53. Example F. Solve for x. a. log 9 (x) = -1 Drop the log and get x = 9 -1 . So x = 1/9 b. log x (9) = -2 When we change the log-form into the exp-form, we say we &quot;drop the log&quot;. The Common Log and the Natural Log

54. Example F. Solve for x. a. log 9 (x) = -1 Drop the log and get x = 9 -1 . So x = 1/9 b. log x (9) = -2 Drop the log and get 9 = x -2 , i.e. 9 = 1 x 2 When we change the log-form into the exp-form, we say we &quot;drop the log&quot;. The Common Log and the Natural Log

55. Example F. Solve for x. a. log 9 (x) = -1 Drop the log and get x = 9 -1 . So x = 1/9 b. log x (9) = -2 Drop the log and get 9 = x -2 , i.e. 9 = So 9x 2 = 1 1 x 2 When we change the log-form into the exp-form, we say we &quot;drop the log&quot;. The Common Log and the Natural Log

56. Example F. Solve for x. a. log 9 (x) = -1 Drop the log and get x = 9 -1 . So x = 1/9 b. log x (9) = -2 Drop the log and get 9 = x -2 , i.e. 9 = So 9x 2 = 1 x 2 = 1/9 x=1/3 or x=-1/3 1 x 2 When we change the log-form into the exp-form, we say we &quot;drop the log&quot;. The Common Log and the Natural Log

57. Example F. Solve for x. a. log 9 (x) = -1 Drop the log and get x = 9 -1 . So x = 1/9 b. log x (9) = -2 Drop the log and get 9 = x -2 , i.e. 9 = So 9x 2 = 1 x 2 = 1/9 x=1/3 or x=-1/3 But the base has to be positive, hence x = 1/3 is the only solution. 1 x 2 When we change the log-form into the exp-form, we say we &quot;drop the log&quot;. The Common Log and the Natural Log

58. 1. b 0 = 1 2. b r · b t = b r+t 3. = b r-t 4. (b r ) t = b rt b t b r Properties of Logarithm Recall the following Rules of Exponents. The corresponding Rules of Logs are.

59. 1. log b (1) = 0 1. b 0 = 1 2. b r · b t = b r+t 3. = b r-t 4. (b r ) t = b rt b t b r Properties of Logarithm Recall the following Rules of Exponents: The corresponding Rules of Logs are:

60. 1. log b (1) = 0 2. log b (x·y) = log b (x)+log b (y) 1. b 0 = 1 2. b r · b t = b r+t 3. = b r-t 4. (b r ) t = b rt b t b r Properties of Logarithm Recall the following Rules of Exponents: The corresponding Rules of Logs are:

61. 1. log b (1) = 0 2. log b (x·y) = log b (x)+log b (y) 3. log b ( ) = log b (x) – log b (y) x y 1. b 0 = 1 2. b r · b t = b r+t 3. = b r-t 4. (b r ) t = b rt b t b r Properties of Logarithm Recall the following Rules of Exponents: The corresponding Rules of Logs are:

62. 1. log b (1) = 0 2. log b (x·y) = log b (x)+log b (y) 3. log b ( ) = log b (x) – log b (y) 4. log b (x t ) = t·log b (x) x y 1. b 0 = 1 2. b r · b t = b r+t 3. = b r-t 4. (b r ) t = b rt b t b r Properties of Logarithm Recall the following Rules of Exponents: The corresponding Rules of Logs are:

63. 1. log b (1) = 0 2. log b (x·y) = log b (x)+log b (y) 3. log b ( ) = log b (x) – log b (y) 4. log b (x t ) = t·log b (x) x y 1. b 0 = 1 2. b r · b t = b r+t 3. = b r-t 4. (b r ) t = b rt b t b r Properties of Logarithm Recall the following Rules of Exponents: The corresponding Rules of Logs are: We veryify part 2: log b (xy) = log b (x) + log b (y), x, y > 0. Proof:

64. 1. log b (1) = 0 2. log b (x·y) = log b (x)+log b (y) 3. log b ( ) = log b (x) – log b (y) 4. log b (x t ) = t·log b (x) x y 1. b 0 = 1 2. b r · b t = b r+t 3. = b r-t 4. (b r ) t = b rt b t b r Properties of Logarithm Recall the following Rules of Exponents: The corresponding Rules of Logs are: We veryify part 2: log b (xy) = log b (x) + log b (y), x, y > 0. Proof: Let x and y be two positive numbers.

65. 1. log b (1) = 0 2. log b (x·y) = log b (x)+log b (y) 3. log b ( ) = log b (x) – log b (y) 4. log b (x t ) = t·log b (x) x y 1. b 0 = 1 2. b r · b t = b r+t 3. = b r-t 4. (b r ) t = b rt b t b r Properties of Logarithm Recall the following Rules of Exponents: The corresponding Rules of Logs are: We veryify part 2: log b (xy) = log b (x) + log b (y), x, y > 0. Proof: Let x and y be two positive numbers. Let log b (x) = r and log b (y) = t, which in exp-form are x = b r and y = b t .

66. 1. log b (1) = 0 2. log b (x·y) = log b (x)+log b (y) 3. log b ( ) = log b (x) – log b (y) 4. log b (x t ) = t·log b (x) x y 1. b 0 = 1 2. b r · b t = b r+t 3. = b r-t 4. (b r ) t = b rt b t b r Properties of Logarithm Recall the following Rules of Exponents: The corresponding Rules of Logs are: We veryify part 2: log b (xy) = log b (x) + log b (y), x, y > 0. Proof: Let x and y be two positive numbers. Let log b (x) = r and log b (y) = t, which in exp-form are x = b r and y = b t . Therefore x·y = b r+t ,

67. 1. log b (1) = 0 2. log b (x·y) = log b (x)+log b (y) 3. log b ( ) = log b (x) – log b (y) 4. log b (x t ) = t·log b (x) x y 1. b 0 = 1 2. b r · b t = b r+t 3. = b r-t 4. (b r ) t = b rt b t b r Properties of Logarithm Recall the following Rules of Exponents: The corresponding Rules of Logs are: We veryify part 2: log b (xy) = log b (x) + log b (y), x, y > 0. Proof: Let x and y be two positive numbers. Let log b (x) = r and log b (y) = t, which in exp-form are x = b r and y = b t . Therefore x·y = b r+t , which in log-form is log b (x·y) = r + t = log b (x)+log b (y).

68. 1. log b (1) = 0 2. log b (x·y) = log b (x)+log b (y) 3. log b ( ) = log b (x) – log b (y) 4. log b (x t ) = t·log b (x) x y 1. b 0 = 1 2. b r · b t = b r+t 3. = b r-t 4. (b r ) t = b rt b t b r Properties of Logarithm Recall the following Rules of Exponents: The corresponding Rules of Logs are: We veryify part 2: log b (xy) = log b (x) + log b (y), x, y > 0. Proof: Let x and y be two positive numbers. Let log b (x) = r and log b (y) = t, which in exp-form are x = b r and y = b t . Therefore x·y = b r+t , which in log-form is log b (x·y) = r + t = log b (x)+log b (y). The other rules may be verified similarly.

69. Exp–log Problems Example G. Simplify. a. log 2 (2 –5 ) = b. 8 log (xy) = c. e 2 + ln(7) = 8

70. Exp–log Problems Example G. Simplify. a. log 2 (2 –5 ) = –5 b. 8 log (xy) = c. e 2 + ln(7) = 8

71. Exp–log Problems Example G. Simplify. a. log 2 (2 –5 ) = –5 b. 8 log (xy) = xy c. e 2 + ln(7) = 8

72. Exp–log Problems Example G. Simplify. a. log 2 (2 –5 ) = –5 b. 8 log (xy) = xy c. e 2 + ln(7) = e 2 ·e ln(7) = 7e 2 8

73. Exp–log Problems Example G. Simplify. a. log 2 (2 –5 ) = –5 b. 8 log (xy) = xy c. e 2 + ln(7) = e 2 ·e ln(7) = 7e 2 Example H. Solve 2.3*ln(2x – 3) + 4.1 = 12.5. Find the approximate numerical solution to 3 significant digits. 8

74. Exp–log Problems Example G. Simplify. a. log 2 (2 –5 ) = –5 b. 8 log (xy) = xy c. e 2 + ln(7) = e 2 ·e ln(7) = 7e 2 Example H. Solve 2.3*ln(2x – 3) + 4.1 = 12.5. Find the approximate numerical solution to 3 significant digits. Isolate the log–term, 2.3*ln(2x – 3) = 8.4 8

75. Exp–log Problems Example G. Simplify. a. log 2 (2 –5 ) = –5 b. 8 log (xy) = xy c. e 2 + ln(7) = e 2 ·e ln(7) = 7e 2 Example H. Solve 2.3*ln(2x – 3) + 4.1 = 12.5. Find the approximate numerical solution to 3 significant digits. Isolate the log–term, 2.3*ln(2x – 3) = 8.4 ln(2x – 3) = 8.4/2.3 8

76. Exp–log Problems Example G. Simplify. a. log 2 (2 –5 ) = –5 b. 8 log (xy) = xy c. e 2 + ln(7) = e 2 ·e ln(7) = 7e 2 Example H. Solve 2.3*ln(2x – 3) + 4.1 = 12.5. Find the approximate numerical solution to 3 significant digits. Isolate the log–term, 2.3*ln(2x – 3) = 8.4 ln(2x – 3) = 8.4/2.3 write this in exp–form 2x – 3 = e 8.4/2.3 8

77. Exp–log Problems Example G. Simplify. a. log 2 (2 –5 ) = –5 b. 8 log (xy) = xy c. e 2 + ln(7) = e 2 ·e ln(7) = 7e 2 Example H. Solve 2.3*ln(2x – 3) + 4.1 = 12.5. Find the approximate numerical solution to 3 significant digits. Isolate the log–term, 2.3*ln(2x – 3) = 8.4 ln(2x – 3) = 8.4/2.3 write this in exp–form 2x – 3 = e 8.4/2.3 2x = e 8.4/2.3 + 3 8

78. Exp–log Problems Example G. Simplify. a. log 2 (2 –5 ) = –5 b. 8 log (xy) = xy c. e 2 + ln(7) = e 2 ·e ln(7) = 7e 2 Example H. Solve 2.3*ln(2x – 3) + 4.1 = 12.5. Find the approximate numerical solution to 3 significant digits. Isolate the log–term, 2.3*ln(2x – 3) = 8.4 ln(2x – 3) = 8.4/2.3 write this in exp–form 2x – 3 = e 8.4/2.3 2x = e 8.4/2.3 + 3 x = (e 8.4/2.3 + 3)/2 ≈ 20.8 8

79. Exp–log Problems ln( Example I. Disassemble the following expression completely. x 2 – 3x – 10 x 2 – 9x )

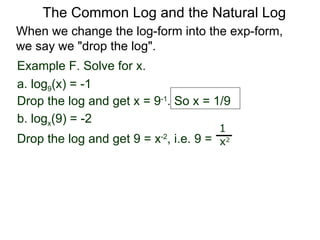
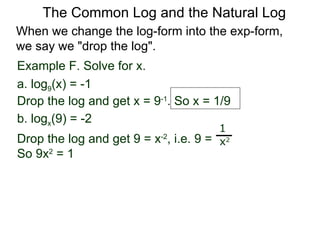
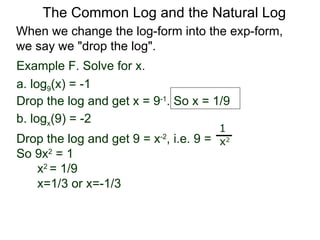
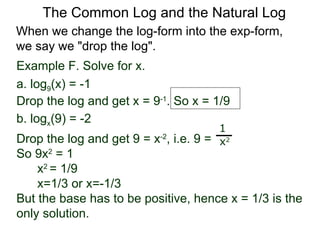
80. Exp–log Problems ln( Example I. Disassemble the following expression completely. x 2 – 3x – 10 x 2 – 9x ) ln[ (x – 5)(x + 2) x(x – 9) ] =

81. Exp–log Problems ln( Example I. Disassemble the following expression completely. x 2 – 3x – 10 x 2 – 9x ) ln[ (x – 5)(x + 2) x(x – 9) ] = ln[(x – 5)(x + 2)] – ½ ln[x(x – 9)] =

82. Exp–log Problems ln( Example I. Disassemble the following expression completely. x 2 – 3x – 10 x 2 – 9x ) ln[ (x – 5)(x + 2) x(x – 9) ] = ln(x – 5) + ln(x + 2) – ln(x)/2 – ln(x – 9)/2 = ln[(x – 5)(x + 2)] – ½ ln[x(x – 9)] =