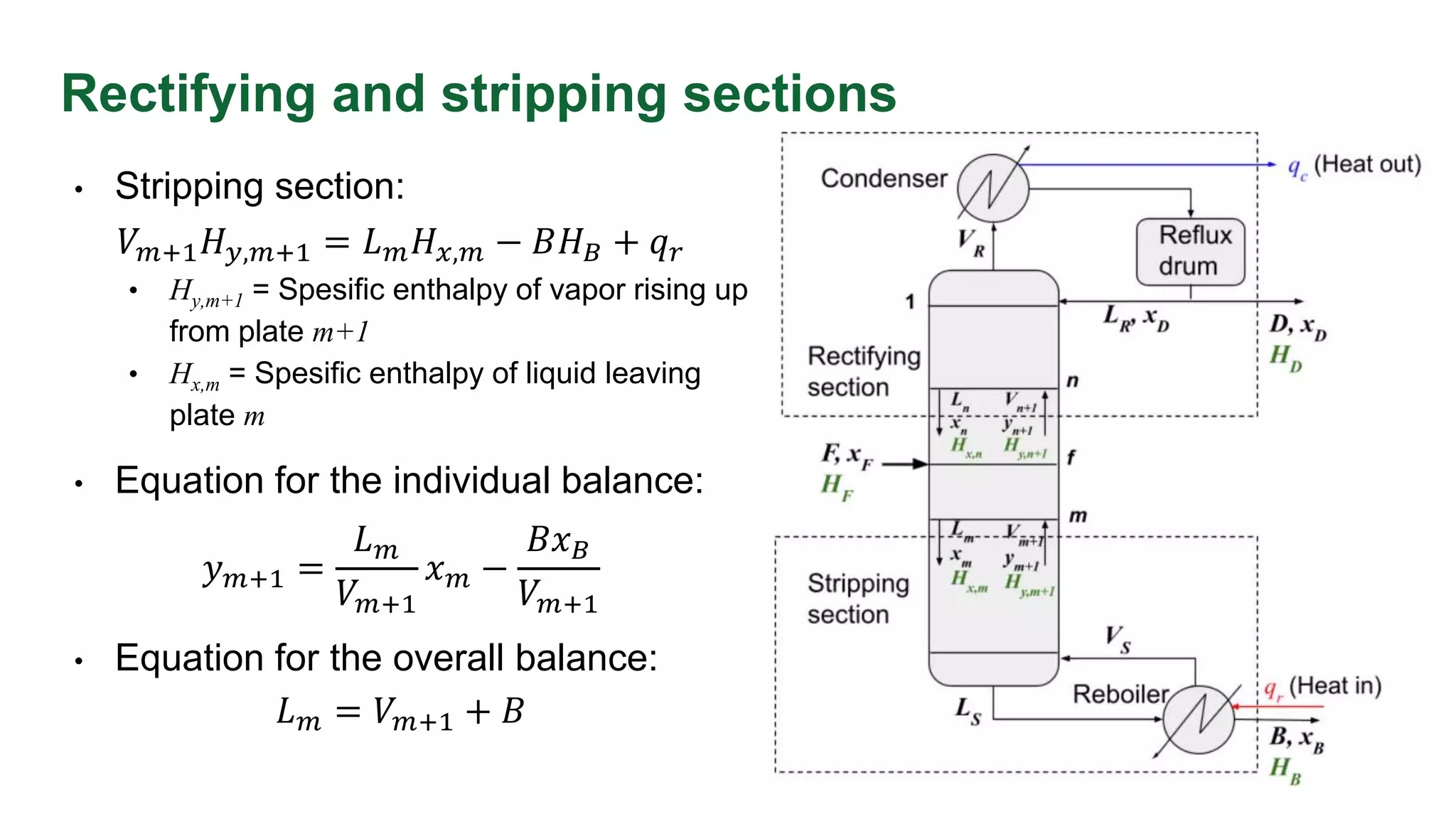
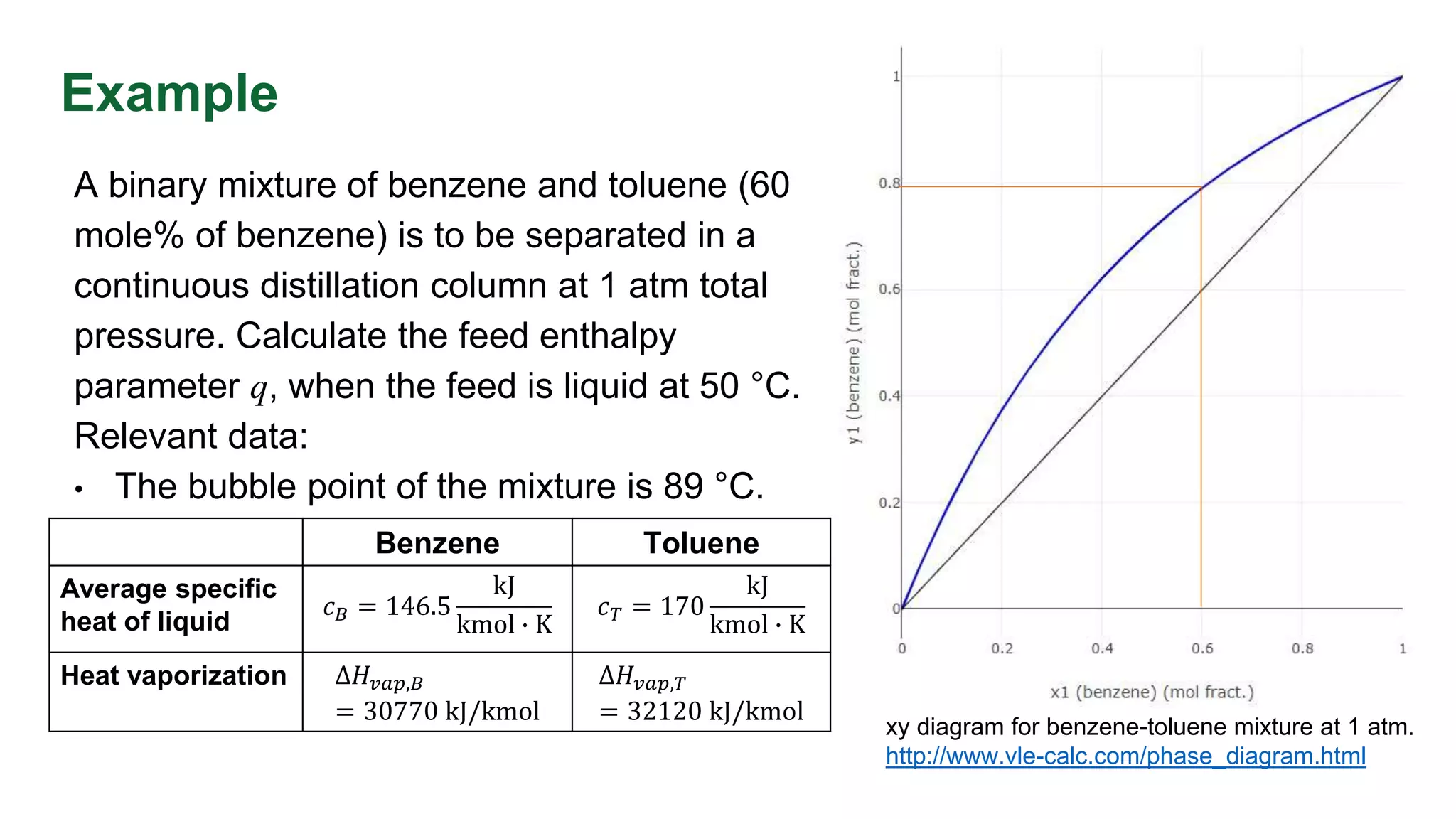
This document discusses enthalpy balances in distillation. It defines enthalpy and provides enthalpy-concentration diagrams. Equations for total and individual enthalpy balances are presented for the rectifying and stripping sections. The document describes how to solve the equations using an iterative approach with enthalpy data. It also discusses how to calculate the feed enthalpy parameter q using enthalpy values. An example problem calculates q for a benzene-toluene mixture.

1. This project has received funding from the European Union’s Horizon 2020
research and innovation programme under grant agreement No 869993.
Enthalpy
balances in
distillation

2. What is enthalpy?
• Enthalpy is a technical term to
describe the energy content of a
material.
• Symbol for enthalpy is H or ΔH.
• In molar enthalpy, the unit is kJ/mol.
• The enthalpy data can be found
from databanks of thermodynamic
properties of substances.
• In distillation, enthalpy data is often
presented in an enthalpy-
concentration diagram.
Enthalpy-concentration diagram for ethanol-
water mixture at 1 atm.
(WolframAlpha Demonstration by Binous, Al-
Baghli & Higgins, 2012 CC BY-NC-SA)

3. Enthalpy in distillation
• In McCabe-Thiele method, we usually
assume constant molal overflow and
the operating lines will then be linear.
• If we don’t make this assumption,
enthalpy balances would be required
in order to perform design calculations.
• The actual variations in the liquid and
vapor streams depend on the enthalpies
of the liquid and vapor mixtures.
• Basic calculations can be made by
enthalpy balance equations.

4. Enthalpy balance equations
• Total enthalpy balance:
𝐹𝐻𝐹 + 𝑞𝑟 = 𝐷𝐻𝐷 + 𝐵𝐻𝐵 + 𝑞𝑐
• HF = Feed enthalpy
• HD = Enthalpy of the distillate
• HB = Enthalpy of the bottom product
• qr = Heat supplied at the reboiler
• qc = Heat removed from the condenser
• When the feed is liquid at the boiling
point, HF is between HD and HB and the
terms FHF and DHD + BHB nearly
cancel.
 qr ≈ qc

5. Rectifying and stripping sections
• Rectifying section:
𝑉𝑛+1𝐻𝑦,𝑛+1 = 𝐿𝑛𝐻𝑥,𝑛 + 𝐷𝐻𝐷 + 𝑞𝑐
• Hy,n+1 = Spesific enthalpy of vapor rising up
from plate n+1
• Hx,n = Spesific enthalpy of liquid leaving plate n
• An alternate form:
𝑉𝑛+1𝐻𝑦,𝑛+1 = 𝐿𝑛𝐻𝑥,𝑛 + 𝑉𝑅𝐻𝑦,𝑅 − 𝑅𝐻𝐷
Using relation 𝑞𝑐 = 𝑉𝑅𝐻𝑦,𝑅 − 𝑅𝐻𝐷 − 𝐷𝐻𝐷
Note: R=LR
• Overall and individual balances:
𝑉𝑛+1 = 𝐿𝑛 + 𝐷 𝑦𝑛+1 =
𝐿𝑛
𝑉𝑛+1
𝑥𝑛 +
𝐷𝑥𝐷
𝑉𝑛+1
LR=R

6. Rectifying and stripping sections
• Stripping section:
𝑉𝑚+1𝐻𝑦,𝑚+1 = 𝐿𝑚𝐻𝑥,𝑚 − 𝐵𝐻𝐵 + 𝑞𝑟
• Hy,m+1 = Spesific enthalpy of vapor rising up
from plate m+1
• Hx,m = Spesific enthalpy of liquid leaving
plate m
• Equation for the individual balance:
𝑦𝑚+1 =
𝐿𝑚
𝑉𝑚+1
𝑥𝑚 −
𝐵𝑥𝐵
𝑉𝑚+1
• Equation for the overall balance:
𝐿𝑚 = 𝑉𝑚+1 + 𝐵

7. Solving equations
• Solving the equation for rectifying section:
𝑉𝑛+1𝐻𝑦,𝑛+1 = 𝐿𝑛𝐻𝑥,𝑛 + 𝑉𝑅𝐻𝑦,𝑅 − 𝑅𝐻𝐷
• A value of xn is chosen and Hx,n is obtained
from an enthalpy-concentration diagram, or
it is calculated from the average specific
heat and the bubble point.
• A satisfactory value for yn+1 can usually be obtained by using the flow rates LR
and VR in the individual material balance: 𝑦𝑛+1 =
𝐿𝑛
𝑉𝑛+1
𝑥𝑛 +
𝐷𝑥𝐷
𝑉𝑛+1
• Hy,n+1 is evaluated from yn+1 and Ln is replaced by 𝑉𝑛+1 − 𝐷 (from total material
balance 𝑉𝑛+1 = 𝐿𝑛 + 𝐷).
• Vn+1 can now be solved from the equation 𝑉𝑛+1𝐻𝑦,𝑛+1 = 𝐿𝑛𝐻𝑥,𝑛 + 𝑉𝑅𝐻𝑦,𝑅 − 𝑅𝐻𝐷
LR=R

8. Solving equations
• Solving the equation for stripping section:
𝑉𝑚+1𝐻𝑦,𝑚+1 = 𝐿𝑚𝐻𝑥,𝑚 − 𝐵𝐻𝐵 + 𝑞𝑟
• Following the same approach:
A value of xm is chosen and Hx,m is obtained
from enthalpy data.
• ym+1 is calculated from equation 𝑦𝑚+1 =
𝐿𝑚
𝑉𝑚+1
𝑥𝑚 −
𝐵𝑥𝐵
𝑉𝑚+1
using LS and VS to
approximate Lm and Vm+1 .
• Lm is replaced by 𝑉𝑚+1 + 𝐵 (from total material balance).
• Hy,m+1 is evaluated from ym+1 .
• Vm+1 can now be solved from the equation 𝑉𝑚+1𝐻𝑦,𝑚+1 = 𝐿𝑚𝐻𝑥,𝑚 − 𝐵𝐻𝐵 + 𝑞𝑟

9. Feed enthalpy condition parameter q
• The feed enthalpy condition parameter q, which is needed when drawing the
feedline (q-line) in McCabe-Thiele method, can be calculated from enthalpies.
• 𝑞 =
𝐻𝑉−𝐻𝐹
𝐻𝑉−𝐻𝐿
• If the feed is saturated liquid, HF = HL and q = 1.
• If the feed is saturated vapor, HF = HV and q = 0.
• For other situations, the feed parameter q can be calculated from enthalpies.
Sub-cooled
liquid
Saturated
liquid
Partially
vaporized
Saturated
vapor
Superheated
vapor
HF < HL
q > 1
HF = HL
q = 1
HV > HF > HL
0 < q < 1
HF = HV
q = 0
HF > HV
q < 0
𝑞 =
𝐻𝑉 − 𝐻𝐹
𝐻𝑉 − 𝐻𝐿
HL = molar enthalpy of liquid
HV = molar enthalpy of vapor HF = molar enthalpy of feed
Enthalpies and values of parameter q with different feed compositions.

10. Example
A binary mixture of benzene and toluene (60
mole% of benzene) is to be separated in a
continuous distillation column at 1 atm total
pressure. Calculate the feed enthalpy
parameter q, when the feed is liquid at 50 °C.
Relevant data:
• The bubble point of the mixture is 89 °C.
xy diagram for benzene-toluene mixture at 1 atm.
http://www.vle-calc.com/phase_diagram.html
Benzene Toluene
Average specific
heat of liquid
𝑐𝐵 = 146.5
kJ
kmol ∙ K
𝑐𝑇 = 170
kJ
kmol ∙ K
Heat vaporization Δ𝐻𝑣𝑎𝑝,𝐵
= 30770 kJ/kmol
Δ𝐻𝑣𝑎𝑝,𝑇
= 32120 kJ/kmol

11. Solution
Let’s take pure liquids at 89 °C (the bubble point of the mixture) as the reference
state. The heat of solution is assumed to be zero (Δ𝐻𝑆 = 0). Let’s take benzene
and toluene and cool them separately from T0 = 89 °C to T = 50 °C.
Δ𝑇 = 50℃ − 89℃ = −39℃
The enthalpy of the feed:
𝑯𝑭 = 0.6 ∙ 146.5
kJ
kmol ∙ K
∙ −39 K + 0.4 ∙ 170
kJ
kmol ∙ K
∙ −39 K = −𝟔𝟎𝟖𝟎. 𝟏
𝐤𝐉
𝐤𝐦𝐨𝐥
The mole fraction of benzene in the saturated vapor in equilibrium with liquid with
x = 0.6 can be read from the xy diagram (given with the example)  y* = 0.79
The enthalpy of saturated vapor 𝐻𝑉 = 0.79 ∙ 30770 + 0.21 ∙ 32120 = 31053.5
kJ
kmol
𝒒 =
𝐻𝑉 − 𝐻𝐹
𝐻𝑉 − 𝐻𝐿
=
31053.5 − (−6080.1)
31053.5 − 0
= 1.19579 … ≈ 𝟏. 𝟐

12. This project has received funding from the European Union’s Horizon 2020
research and innovation programme under grant agreement No 869993.
References
Dutta, B. K. 2007. Principles of mass transfer and separation processes. New Delhi: Prentice-Hall,
pp. 340-343, 367-371.
McCabe, W. L., Smith, J. C. & Harriott,, P. 2005. Unit Operations of Chemical Engineering. 7 th
Edition. New York: McGraw-Hill, pp. 694-701.
Videos:
• Enthalpy Concentration Diagram Example: https://youtu.be/EwlV9RGDcvM (7:56)
• What is Enthalpy? https://youtu.be/SV7U4yAXL5I (11:23)
• Reading an enthalpy-concentration diagram: https://youtu.be/YTlXAMtKWTQ (8:06)